1. 서론
일반적으로 해안지역에 설치되는 직립방파제 피해의 66%는 활동파괴에 의해 발생한다고 보고되었다(Takayama and Higashira, 2002). 직립방파제의 활동파괴는 주로 뱀이 기어 가는 형태의 사행 피해(meandering damage)가 많으며, 많은 학자들이 그 원인을 회절파(diffracting waves)로 보고 있다(Ito and Tanimoto, 1971; Jung et al., 2016; Choi et al., 2020; Jung et al., 2021).
방파제 주변의 회절은 입사파가 진행함에 따라 방파제 배후에서 나타나는 Shadow zone에서 입사파의 에너지 이동에 의해 발생하고, 방파제 전면에서 중복파가 발생함에 따라 중복파 영역에서 입사파만 존재하는 영역으로 에너지가 이동하여 또한 발생한다(Jung and Lee, 2020). 방파제 주변에서 발생하는 중력파의 회절현상은 Lamb(1945)이 Sommerfeld(1896)에 의해 제시된 빛의 회절이론으로부터 반무한방파제에 수직으로 입사하는 규칙파에 대한 해석해를 제시하였다. Penney and Price(1952)는 반무한방파제 및 양익방파제에 비스듬히 입사하는 규칙파에 대한 회절의 해석해를 제시하였다. Yu(1995)는 투수성 방무한방파제에 수직으로 입사하는 규칙파의 회절에 대한 근사해를 제시하였으며, McIver(1999)는 Yu (1995)의 연구를 확장하여 투수성 반무한방파제에 비스듬히 입사하는 규칙파의 회절에 대한 근사해를 제시하였다. 이후 McIver(2005)는 다열의 이안제에 비스듬히 입사하는 규칙파의 근사해를 제시하였다. Lee and Kim(2006)은 다방향 불규칙파를 대상으로 반무한방파제 주변의 회절에 대해 수치적으로 검토하였다. Suh and Kim(2008)은 방파제 전면에서 부분 반사가 발생하는 경우 반무한방파제에 수직으로 입사하는 규칙파의 회절에 대한 해석해를 제시하였으며, Kim et al.(2011)은 전면에 부분반사가 발생하는 반무한방파제 및 양익방파제에 비스듬히 입사하는 규칙파의 회절에 대한 해석해를 제시하였다.
직립방파제에 작용하는 파력에 대해서는 주로 방파제 단면에 작용하는 파력의 분포형상에 대한 연구(Goda, 1975; Allsop et al., 1996; Wood et al., 2000; Cuomo et al., 2010)가주로 수행되었다. 회절에 의한 공간적인 파력의 분포형상에 대해서는 반무한방파제를 대상으로 Jung et al.(2016) 및 Jung et al.(2021)에 의해 연구가 수행되었다. 특히 Jung et al.(2021)은 직립 방파제 전면과 후면의 회절파의 영향을 모두 고려하였으며, 반무한방파제에 작용하는 최대 파력은 회절과 공간적 파력분포를 고려하지 않은 경우보다 1.34배 크다는 사실을 밝혔다.
일반적으로 바다에 건설되는 직립방파제는 반무한방파제 뿐만 아니라 이안제 형식도 많이 건설되고 있다. 따라서 본 연구에서는 불투과성 직립 이안제 주변에서 발생하는 회절 영향을 고려한 파력 분포에 대해 검토하였다. 이안제에서 발생하는 회절의 해는 반무한방파제의 회절에 대한 해를 중첩하여 유도하였다. 이안제 전면과 후면에 작용하는 회절파의 영향을 모두 고려하였다. 변수 설명 및 이안제 주변의 파랑변형에 대한 해석해의 유도과정은 2장에서 기술하였다. 3장에서는 회절과 이안제 전·후면의 파력차를 고려하여 이안제에 작용하는 파력에 대한 해석해를 유도하였다. 4장에서는 수치해석을 통해 이안제 상대길이에 따른 파력에 대해 기술하고, 결론에서는 본 연구의 핵심적인 성과에 대해 설명하였다.
2. 이안제 주변의 회절파에 대한 해석해 유도
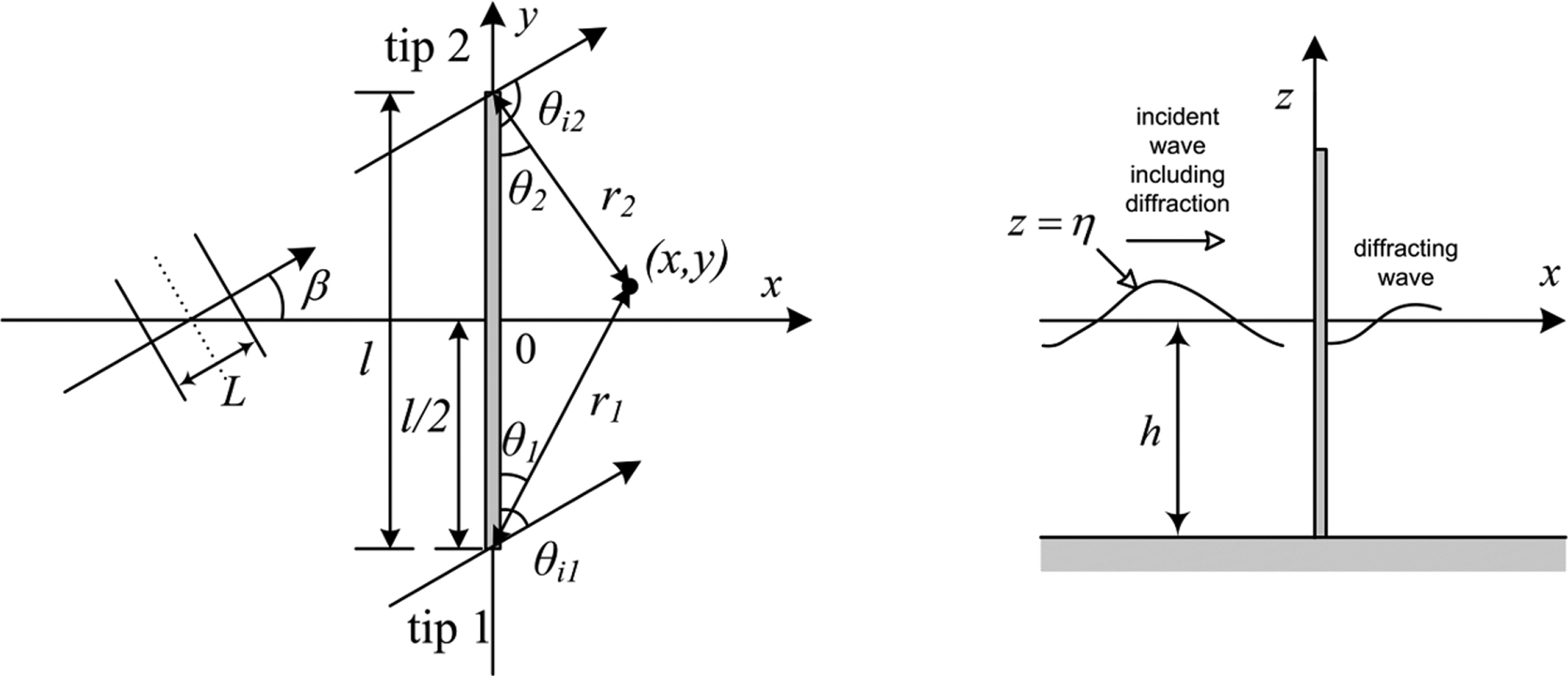
직립 이안제에 작용하는 파력의 공간적 변화를 검토하기 위해 먼저 이안제 주변의 회절에 대한 이론적 연구를 수행하였다. 이안제 주변의 회절은 이안제 양쪽 두부(head)에 반무한 방파제 주변의 회절에 대한 해를 각각 중첩시켜 유도할 수 있다. 해석해 유도를 위한 개념도 및 각 변수에 대한 설명은 Fig. 1과 같다. Fig. 1에서 L은 파장(wavelength), h는 수심 (water depth), η는 자유수면변위(free surface displacement), β는 구조물에 수직인 법선과 파향선이 이루는 각, l은 이안제의 길이, θi1은 한쪽 방파제 두부(tip 1)에서 파향선과 방파 제가 이루는 각 그리고 θi2는 다른쪽 방파제 두부(tip 2)에서 파향선과 방파제가 이루는 각을 각각 뜻한다.
자유수면과 바닥에서 선형의 경제조건을 만족하는 Laplace 방정식의 해는 다음과 같다.
여기서, αi는 입사파의 진폭(wave amplitude), g는 중력가속도, ω는 각진동수(angular frequency) 그리고 k는 파수(wave number)를 각각 뜻한다. F(x, y)는 다음과 같이 주어진 Helmholtz 방정식을 만족한다.
Kim et al.(2011)에 의해 제시된 방파제에서의 부분반사 경계 조건은 다음 식과 같다.
여기서, n은 방파제 전면에서 단위법선벡터(unit normal vector), Kr은 방파제 전면에서 반사계수를 나타낸다. 식(3)을 이용하고 직교 좌표계(cartesian coordinate system)를 포물선 좌표계(parabolic coordinate system)로 변환하여 식(2)를 해석한 이후 다시 극 좌표계(polar coordinate system)로 변환 하면 tip 1을 원점 및 두부로 하는 반무한방파제 회절에 대한 해를 다음과 같이 구할 수 있다(Kim et al., 2011).
여기서, r1은 임의의 한 점과 원점(방파제 tip 1) 사이의 거리, θ1은 임의의 한점과 원점을 연결한 선이 y축과 이루는 각도를 나타내며, 이는 Fig. 1을 참고할 수 있다. 그리고 u는 식의 유도과정에서 발생하는 매개변수이며, ψ와 ψ'는 각각 입사파 및 반사파의 위상정보를 담고 있다.
방파제 tip 2를 원점 및 두부로 하는 반무한방파제 회절에 대한 해석해는 다음과 같다.
여기서, r2는 임의의 한 점과 원점(방파제 tip 2) 사이의 거리, θ2는 임의의 한점과 원점을 연결한 선이 - y축과 이루는 각도를 나타낸다. 식(6)은 Fresnel 적분을 포함하며, 이는 Euler 공식을 이용하여 실수부와 허수부를 분리한 뒤 무한급수 형태의 각 해를 계산하여 풀 수 있다. 식(6)의 f(ψ)는 다음과 같은 관계를 만족한다(Penney and Price, 1952).
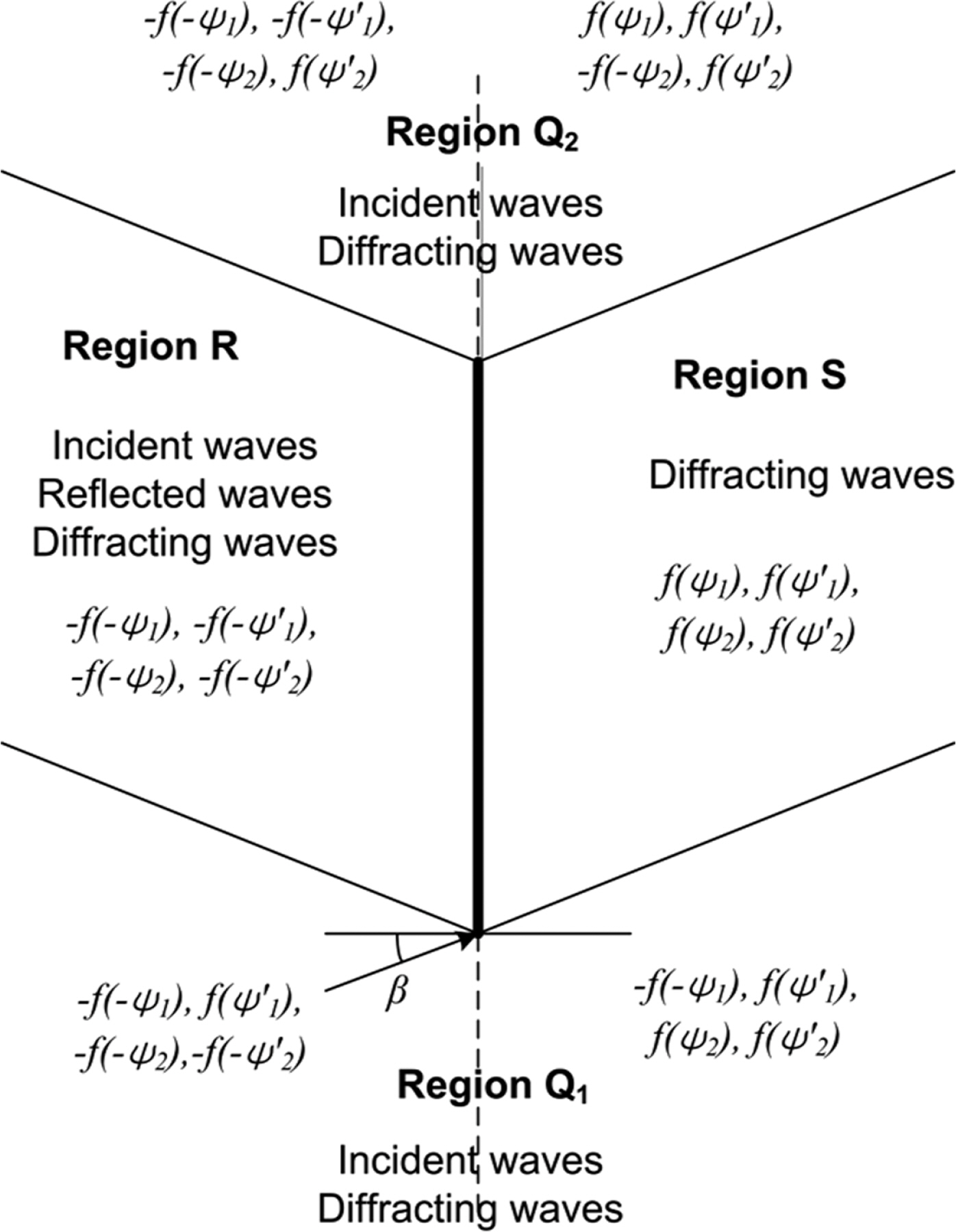
이안제 주변의 파랑 성분은 Fig. 2에 정리하였다. 이안제 전면(Region R)에서는 입사파, 반사파 및 입사파, 반사파의 회절성분이 존재하며, 이안제 후면(Region S)에서는 입사파 및반사파의 회절성분이 존재한다. 그리고 이안제 측면(Region Q1 및 Q2)에서는 입사파 및 입사파, 반사파의 회절성분이 존재한다. 이안제 전면에서 해는 식(4)와 식(9)를 합성하여 정리할 수 있다. 두 식을 합성할 때 각 식에는 입사파 및 반사파가 모두 포함되어 있기 때문에 두 식을 합한 후 입사파 및 반사파 한 성분씩 삭제한 후 정리하면 다음 식과 같다.
(14)
여기서, 첫번째 및 두번째 항은 각각 입사파와 반사파 성분을 의미한다. 세번째 및 네번째 항은 방파제 tip 1에서 회절된 입사파 및 반사파의 회절성분을 각각 의미한다. 다섯번째 및 여섯번째 항은 방파제 tip 2에서 회절된 입사파 및 반사파의 회절성분을 각각 의미한다. 방파제 후면(Region S)에서 회절의 해는 다음과 같다.
(15)
식(15)에서 첫번째 및 두번째 항은 tip 1에서 회절된 입사파및 반사파의 회절성분이며, 세번째 및 네번째 항은 tip 2에서 회절된 입사파 및 반사파의 회절성분이다. 이안제 측면 (Region Q1 및 Q2)에서 회절의 해는 x > 0인 경우 식(16) 및 (17)과 같고, x ≤ 0인 경우 식(18) 및 (19)와 같다.
(16)
(17)
(18)
(19)
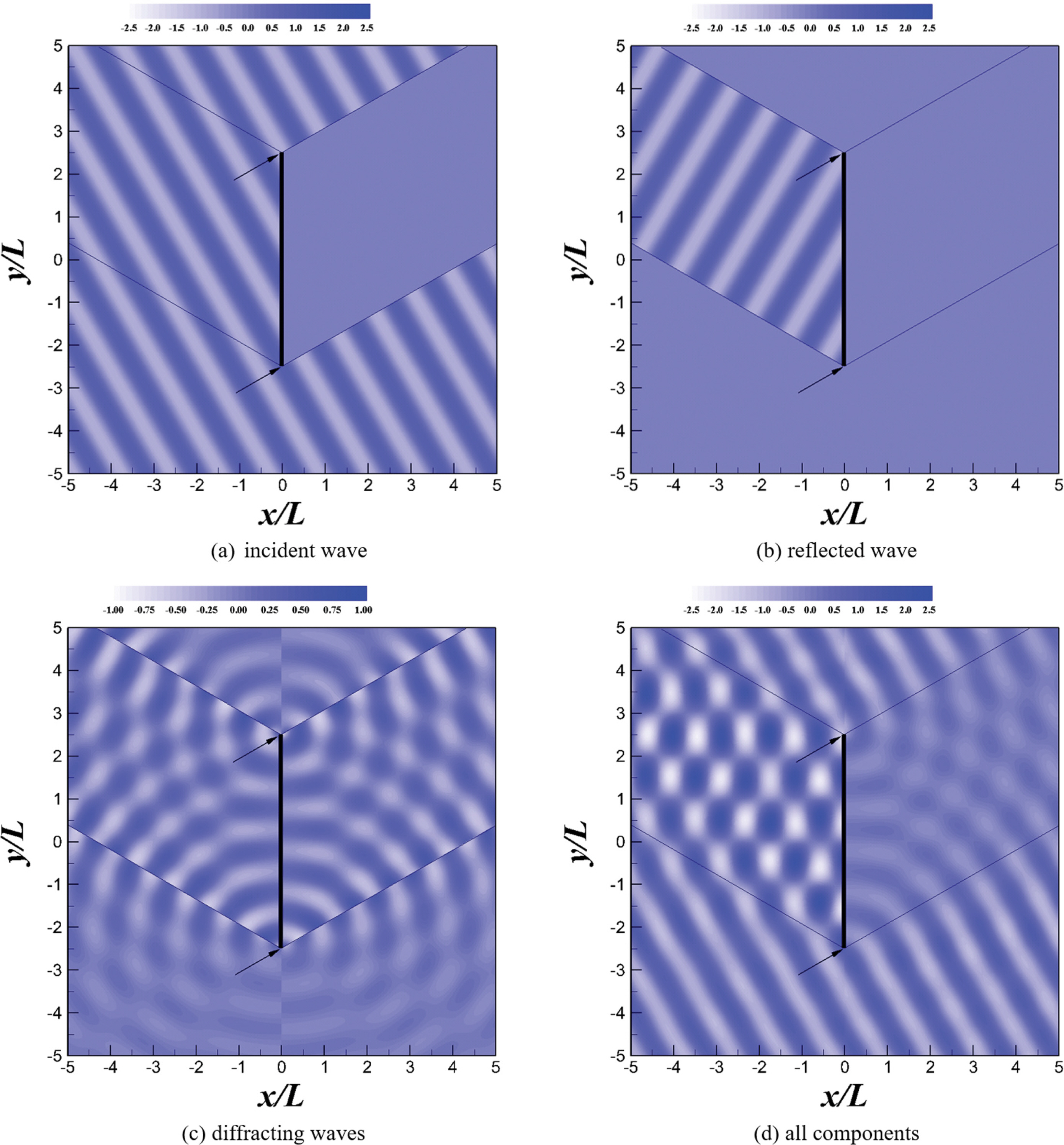
식(14)~(19)를 이용하여 이안제 주변에서 무차원 자유수면 변위를 Fig. 3에 나타내었다. 무차원 자유수면변위(η/αI)와 무차원 진폭α/αI)은 다음 식과 같이 정의된다.
Fig. 3에서 파랑의 입사각(β)은 30°, 수심(h)은 20 m, 입사파 주기(T)는 10초, 이안제의 길이(l)는 5 파장(L)으로 가정하였으며, 반사계수(Kr)는 1을 적용하였다. Fig. 3(a)~3(c)는 각각 입사파, 반사파 및 회절파의 무차원 자유수면변위를 나타내며, Fig. 3(d)는 각 성분들을 모두 합성한 합성파의 무차원 자유수면변위를 나타낸다. Fig. 3(c)에서 tip 1에서 회절된 회절파의 방파제 전면 및 후면에서 위상차이가 180도이고, tip 2에서 회절된 회절파의 방파제 전면 및 후면에서 위상차이가 마찬가지로 180도인 것을 확인할 수 있다. 이는 Jung et al. (2021)이 반무한방파제를 대상으로 해석한 결과와 동일하며, 방파제 전면 및 후면의 회절파 영향을 고려하면 직립 이안제에 작용하는 파력이 입사파 및 반사파만 고려했을 때보다 훨씬 커질 수 있음을 의미한다.
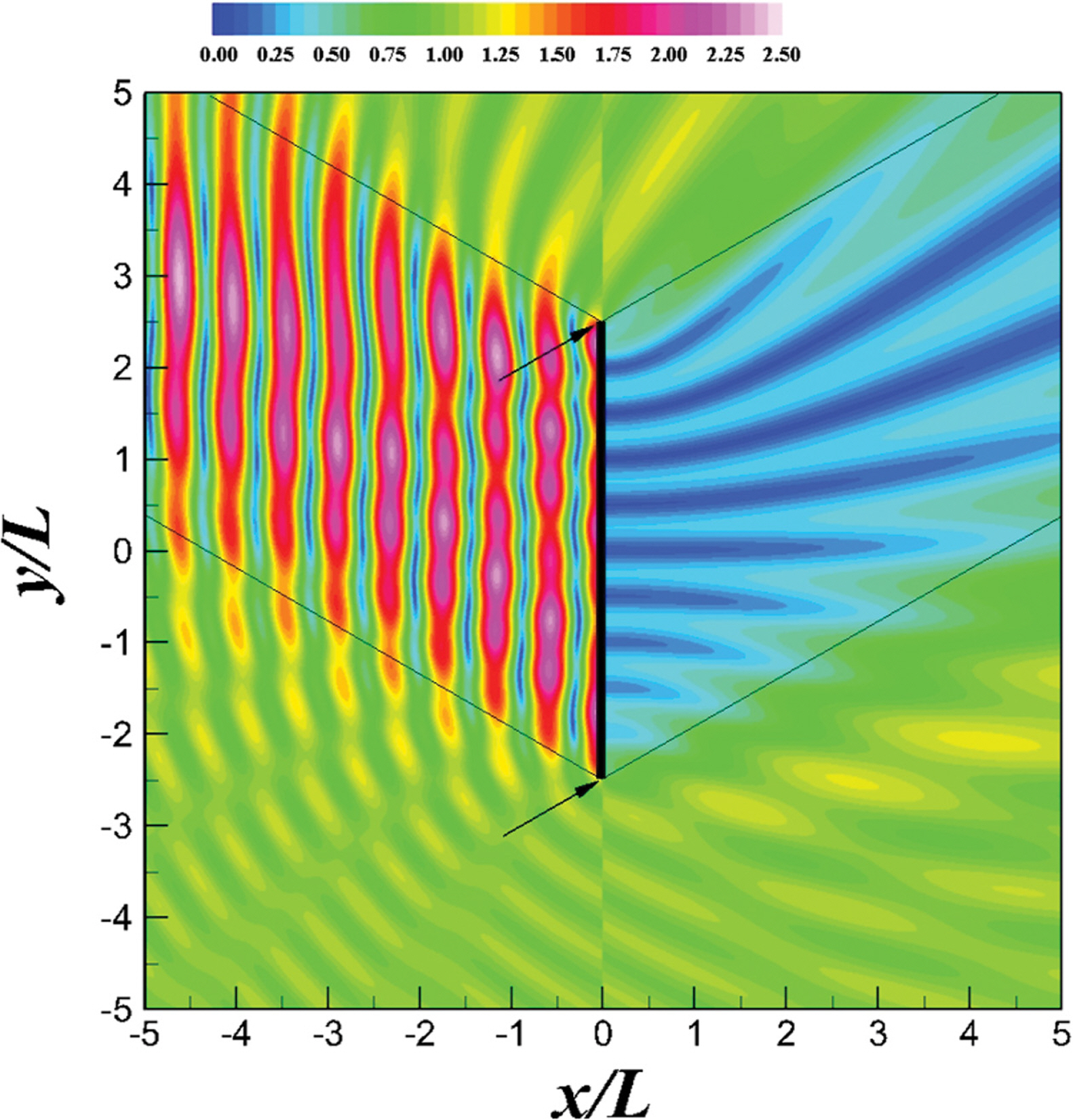
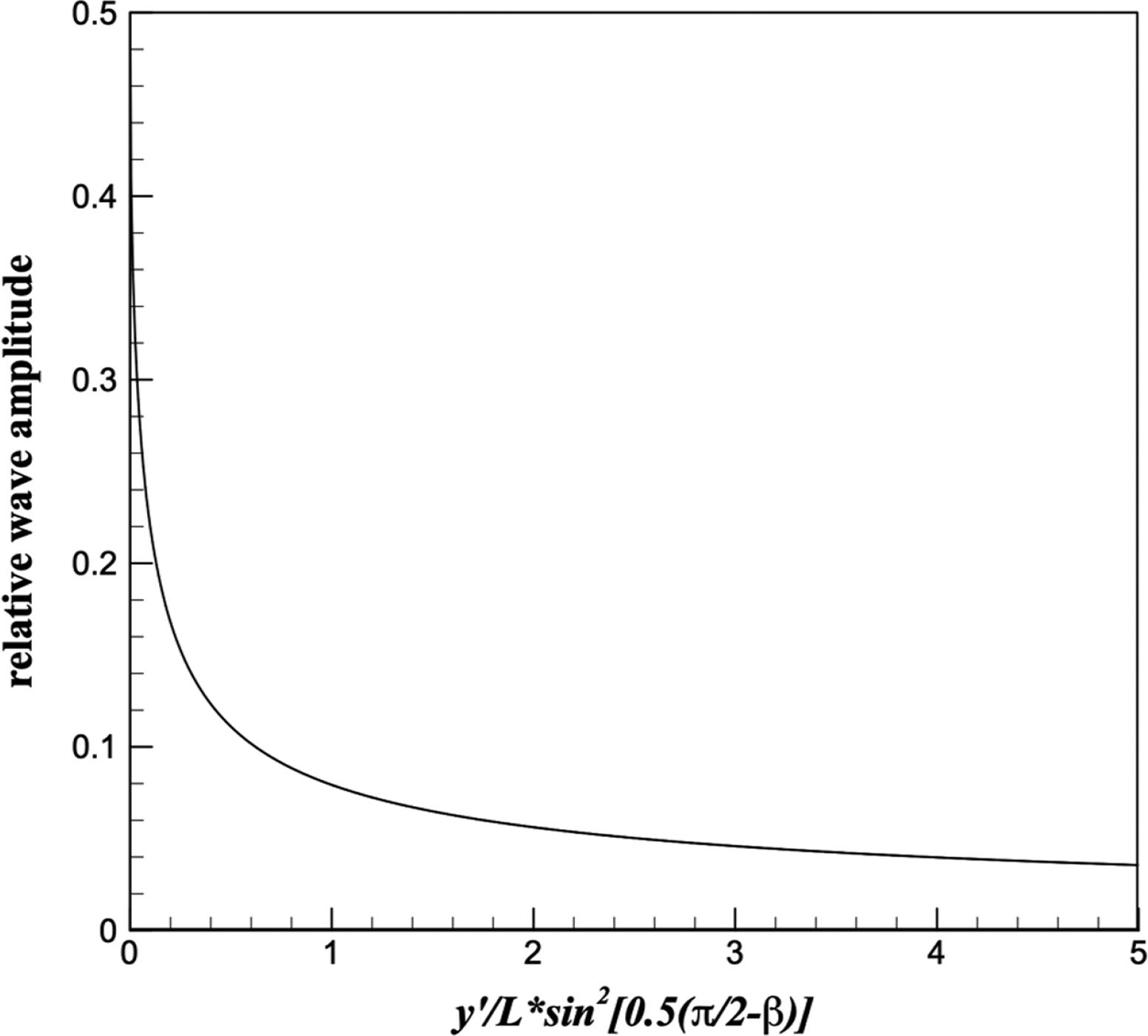
직립 이안제 주변에서 무차원 진폭은 Fig. 4와 같다. 이안제 전면에서 진폭의 크기가 규칙적으로 변화하는 것을 확인할 수 있는데, 이는 입사파 및 반사파와 회절파의 위상 차이 때문에 으로 나타나는 현상이다. 이안제 후면에서 진폭의 크기도 규칙적으로 변화하는데, 이는 이안제 양쪽 끝에서 회절된 각 회절파의 간섭에 의해서 나타나는 현상이다. 이안제 전면에서 최대 진폭은 2.48로 나타났다. 이는 회절파를 무시했을 경우에 비해 이안제 전면에 약 24%의 추가적인 파력이 작용할 수 있음을 의미한다. 그리고, 이안제 후면의 파력까지 함께 고려했을 때에는 24% 이상의 추가 파력이 작용할 것이다. 본 연구에서 이안제 주변의 회절을 해석하기 위해 반무한방 파제의 회절에 대한 해를 중첩하였다. 따라서, 본 연구에서 제시하는 이안제의 회절에 대한 해에는 방파제 후면으로 회절된 파가 다시 전면으로 회절하는 현상은 포함되지 않았다. 따라서, 본 연구의 이안제 회절에 대한 해는 이안제의 길이가 충분히 길어서 회절파의 회절의 영향이 작은 경우에만 타당할 것이다. Fig. 5에는 Jung and Lee(2020)가 제시한 파랑의 입사각과 반무한방파제의 위치에 따른 무차원변수(y'/L{sin[0.5 (π/2-β)]}2)에 대해 중복파의 진폭으로 무차원화된 회절파의 상대진폭을 도시하였다. 이안제의 한쪽 두부에서 회절된 회절파의 상대진폭은 방파제 두부(y'/L{sin[0.5(π/2-β)]}2 = 0, y' = y + l/2)에서 0.5로 최대이며 방파제를 따라 전파하면서 크게 감소한다. 특정 길이의 이안제에서 회절이 발생한 두부의 반대쪽에서 회절파의 상대진폭이 중복파 대비 0.05 이내라면, 회절파가 다시 회절된 파의 진폭은 중복파의 5% 이내가 될것이다. 이 경우 회절파가 다시 회절된 파랑의 효과가 크지 않음을 알 수 있다. Fig. 5에서 무차원변수 y'/L{sin[0.5(π/2-β)]}2 가 2.4715보다 큰 위치에서는 회절파의 상대진폭이 0.05 이하로 나타났다. 즉, 이안제의 길이와 입사각을 고려했을 때무차원변수 y'/L{sin[0.5(π/2-β)]}2 가 2.4715보다 큰 경우에는 회절파가 다시 회절된 효과를 무시할 수 있다.
3. 이안제에 작용하는 파력
본 장에서는 회절을 고려하여 직립 이안제에 작용하는 파력에 대해 검토하였다. 이안제 전면(region R)에는 입사파, 반사파 및 이안제 양쪽 두부에서 발생하는 회절파가 존재하며, 이안제 후면(region S)에는 이안제 양쪽 두부에서 발생하는 회절파 성분들만 존재한다. 이안제 전면에서 입사파 및 반사파의 속도포텐셜은 직교좌표계에서 다음과 같이 표현된다.
여기서, αi(x, y)와 αr(x, y)은 각각 입사파 및 반사파의 진폭을 뜻하며, ω는 각진동수,g는 중력가속도, 그리고 Kr은 반사계수를 나타낸다.
이안제 전면(x = 0, θ1 = θ2 = 2π)에서 입사파 및 반사파의 회절성분에 대한 속도포텐셜은 식(14)를 이용하여 직교좌표 계에서 다음과 같이 정리할 수 있다.
(24)
그리고, 이안제 후면(x = 0, θ1 = θ2 = 0)에서 입사파 및 반사파의 회절성분에 대한 속도포텐셜은 식(15)를 이용하여 직교 좌표계에서 다음과 같이 표현된다.
(25)
여기서, f(ψ)는 식(6)과 같이 정의되는 회절성분의 상대진폭을 나타내는 함수이다. ψ1과 ψ1'는 각각 tip 1에서 입사파 및 반사파의 회절에 대한 매개변수이며, ψ2과 ψ2'는 각각 tip 2에서 입사파 및 반사파의 회절에 대한 매개변수이다. 아래첨자 f 와 l은 각각 방파제 전면(front side)과 후면(lee side)을 각각 뜻한다.
여기서, sin [ 1 2 ( 3 π 2 + β ) ] = - sin [ 1 2 ( - π 2 + β ) ] sin [ 1 2 ( 3 π 2 - β ) ] = - sin [ 1 2 ( π 2 + β ) ]
이안제 전면에서 입사파, 반사파 및 각 회절성분을 모두 포함하는 총 속도포텐셜은 식(21)~(24) 및 식(31)을 이용하여 다음과 같이 나타낼 수 있다.
이안제 전면에서 파압은 다음과 같다.
이안제 후면에서 속도포텐셜은 식(25)와 식(32)를 이용하여 다음과 같이 표현된다.
이안제 후면에서 파압은 다음과 같이 유도된다.
이안제 단위폭당 작용하는 파력은 파압을 수직 방향으로 적분하여 구할 수 있으며, 이안제 전면 및 후면에서 단위폭당 파력은 다음과 같다.
이안제에 작용하는 단위폭단 총 파력은 방파제 전면과 후면의 단위폭당 파력을 합성하여 구할 수 있으며, 다음과 같이 표현된다.
회절을 무시했을 때 이안제에 작용하는 단위폭당 파력은 다음과 같다.
이안제 전면 및 후면에 작용하는 정수압을 제외한 단위폭당 파력과 전·후면의 파력을 합성한 단위폭당 총 파력은 "회절을 무시했을 때 단위폭당 파력"으로 무차원화 할 수 있으며, 각각 다음과 같이 표현된다.
4. 수치해석 결과
4.1 이안제에 작용하는 규칙파의 파력
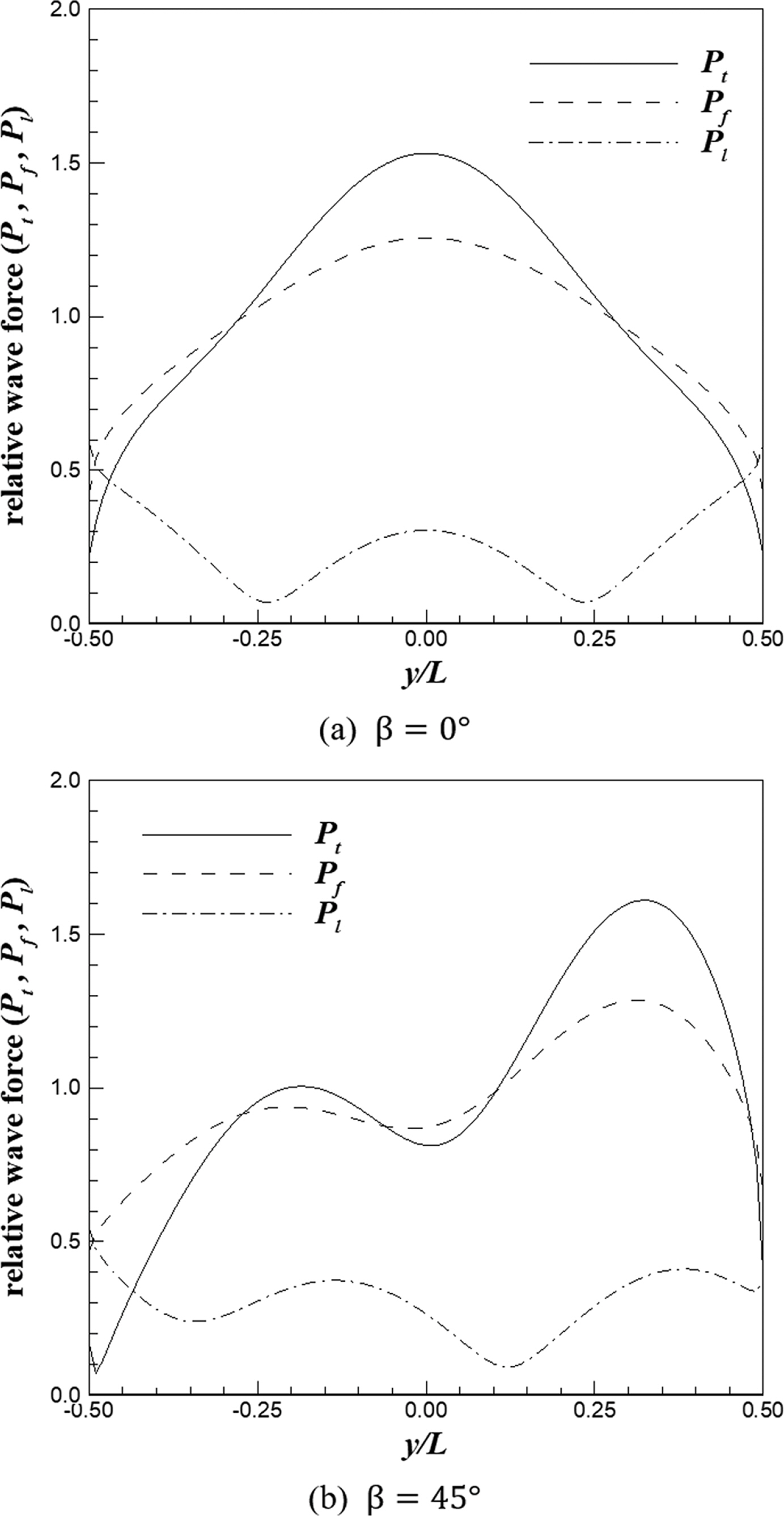
이안제에 작용하는 규칙파의 파력을 수치해석을 통해 검토하였다. 수치해석을 위한 조건으로 수심은 10 m, 입사파의 진폭은 1.0 m, 주기는 10초로 설정하였다. 계산을 위한 공간 간격은 0.01 L을 적용하였다. 검토 결과는 Figs. 6~8에나타내었다. 그림에서 실선은 이안제 전·후면의 파력을 합성한 총 파력을 나타내며, 파선은 이안제 전면에 작용하는 파력, 일점쇄선은 이안제 후면에 작용하는 파력을 각각 나타낸다.
이안제의 상대 길이(l/L)가 1.0 인 경우 작용 파력은 Fig. 6과 같다. 이안제는 y = 0인 축을 기준으로 양쪽으로 대칭이기 때문에, 입사각이 0도인 경우 공간적 파력 분포는 y = 0인 축을 기준으로 대칭인 형태를 보인다(Fig. 6(a)). 입사각이 0도일 때(이안제에 수직으로 입사할 때) 이안제 중앙에서 총 파력이 1.53으로 최대 파력이 발생한다. 이는 회절을 고려하지 않았을 때보다 회절을 고려했을 때 이안제에 작용하는 파력이 53% 더 큼을 의미한다. 입사각이 45도인 경우에는 y/L = 0.33인 위치에서 최대 파력이 1.61로 나타났다. 파랑이 이안제에 비스듬히 입사할 경우 이안제에 작용하는 파력의 분포는 비대칭 형상을 보였다.
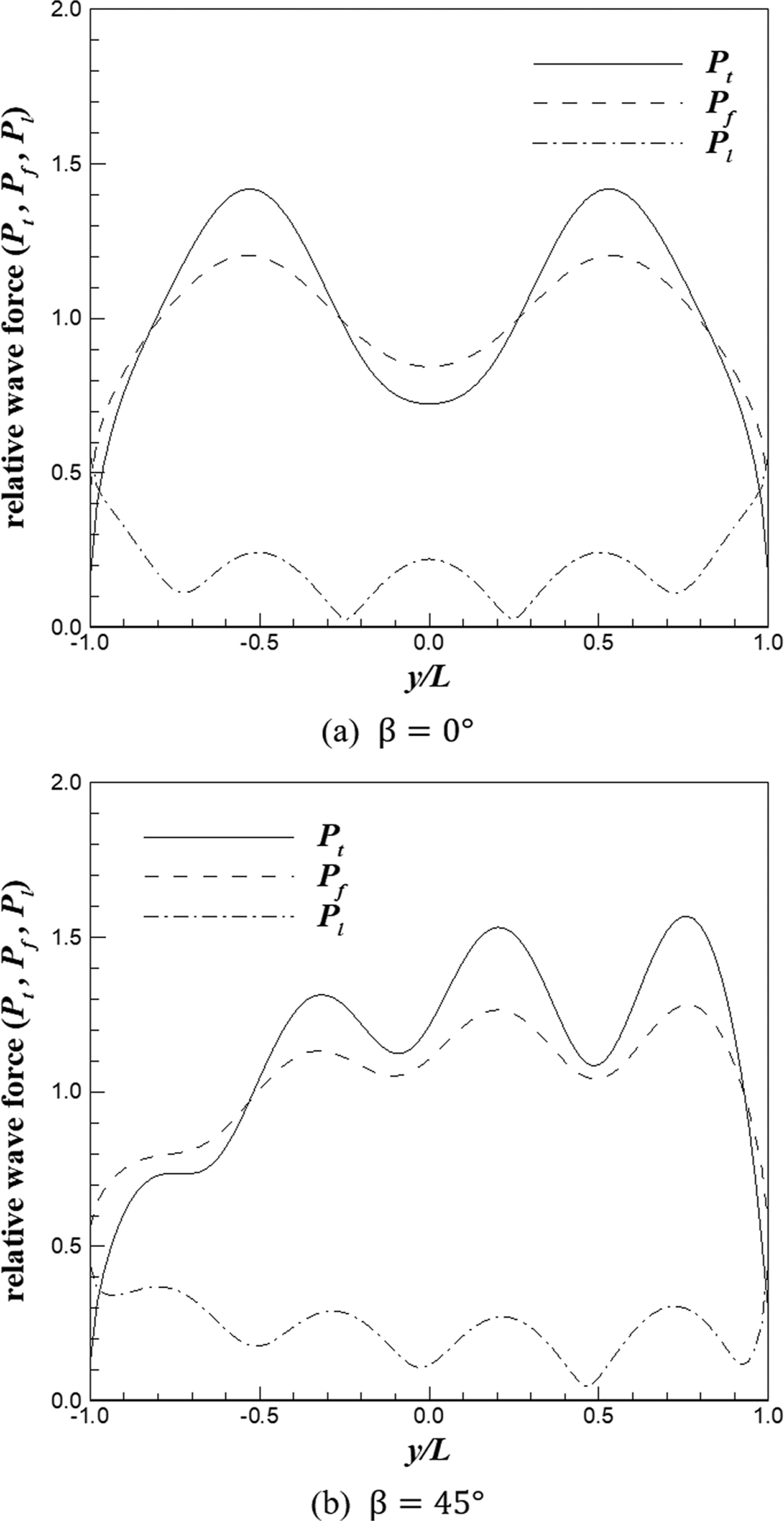
이안제의 상대 길이가 2.0인 경우 작용 파력은 Fig. 7과 같으며, 총 파력의 최대치는 1.42로 계산되었다. 이안제의 상대 길이가 2.0인 경우에도 파랑이 이안제에 비스듬히 입사할 경우 파력의 분포는 비대칭 형상을 보였다. 입사각이 45도인 경우 최대 파력은 1.57로 계산되었다.
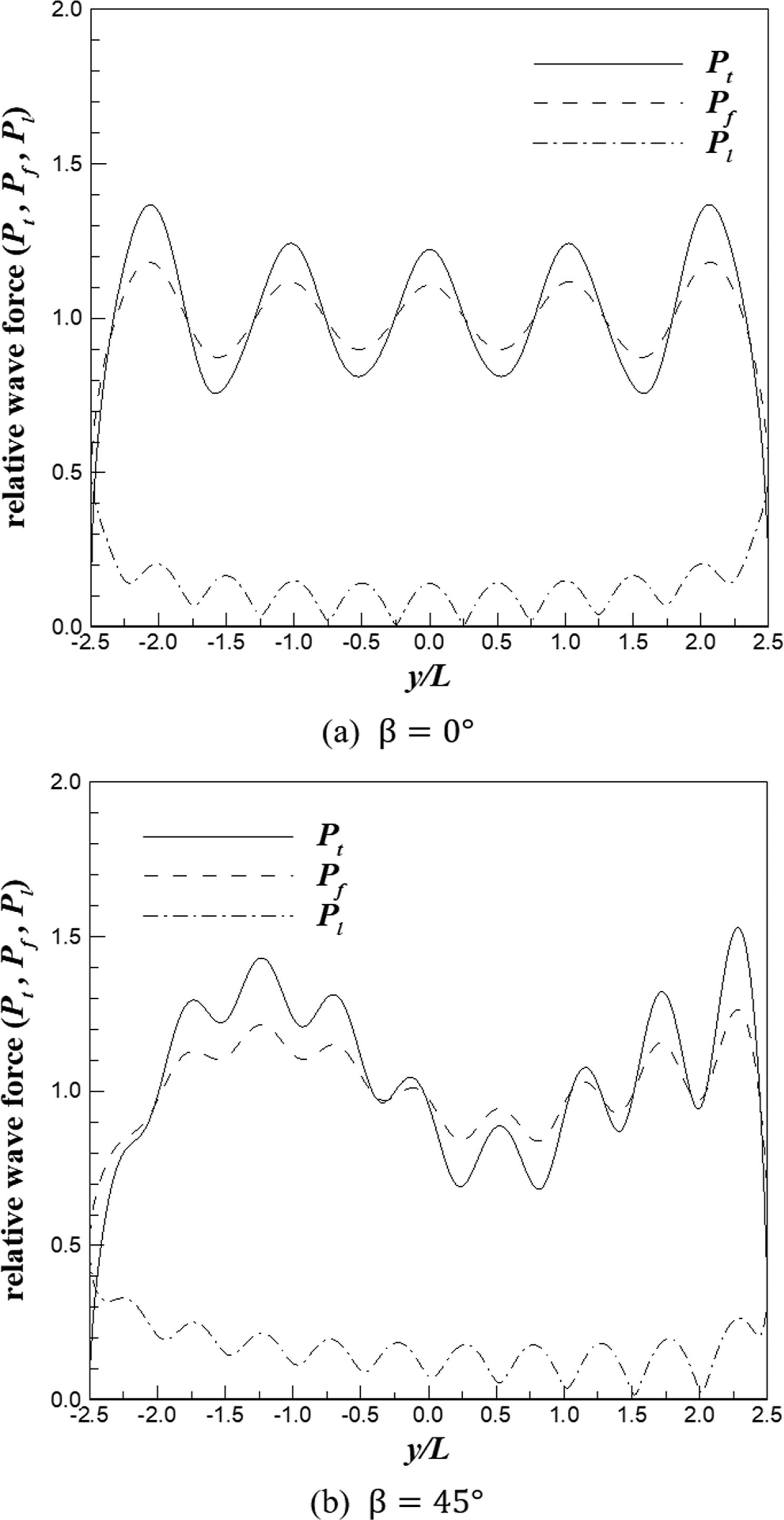
이안제의 상대 길이가 5.0인 경우 작용 파력은 Fig. 8과 같다. 파랑의 입사각이 0도일 때 이안제 전면 및 후면에 작용하는 회절파의 파력 분포는 규칙적으로 변화하는 형태를 보인다. 이안제 전면의 경우 회절파의 파봉(wave crest)과 중복파의 파봉 또는 회절파의 파곡(wave trough)과 중복파의 파곡이 만나는 위치에서는 파력이 중첩되어 크게 나타나고, 회절파의 파봉과 중복파의 파곡, 또는 중복파의 파봉과 회절파의 파곡이 만나는 위치에서는 파력이 상쇄되어 작게 나타난다. 이안제 후면의 경우 양쪽 방향에서 회절된 회절파의 파봉과 파봉 또는 파곡과 파곡이 만나는 위치에서는 파력이 중첩되어 크게 나타나고, 회절파의 파봉과 파곡이 만나는 경우에는 파력이 상쇄되어 작게 나타난다. 입사각이 0도인 경우 최대 파력은 1.37로 계산되었으며, 입사각이 45도인 경우에는 1.53으로 계산되었다.
4.2 이안제에 작용하는 불규칙파의 파력
본 절에서는 이안제에 작용하는 불규칙파의 파력에 대해 검토하였다. 이안제에 작용하는 불규칙파의 상대파력은 다방향 불규칙파를 기준으로 다음 식과 같이 정의된다.
(44)
(45)
(46)
여기서, Pr,f는 이안제 전면, Pr,l는 이안제 후면, 그리고 Pr,t는 이안제 전면과 후면 파력의 합성 파력을 각각 나타낸다. S(f, β)는 다방향 불규칙파의 에너지 스펙트럼으로 다음 식과 같이 정의된다.
위 식에서 S(f)는 주파수 스펙트럼, G(f, β)는 방향 스펙트럼을 각각 뜻한다. 본 연구에서 주파수 스펙트럼은 Hasselmann et al.(1973)이 제시한 JONSWAP(Joint North Sea Wave Project) 스펙트럼을 적용하였으며, 다음 식과 같이 표현된다.
여기서
여기서, γ는 첨두증진계수, Tp는 첨두 주기를 뜻한다. 방향 스펙트럼으로는 Lee et al.(2010)이 제시한 비대칭 스펙트럼을 적용하였으며, 다음식과 같이 표현된다.
여기서, μ는 비대칭 계수, smax는 최대 분포계수를 각각 뜻한다.
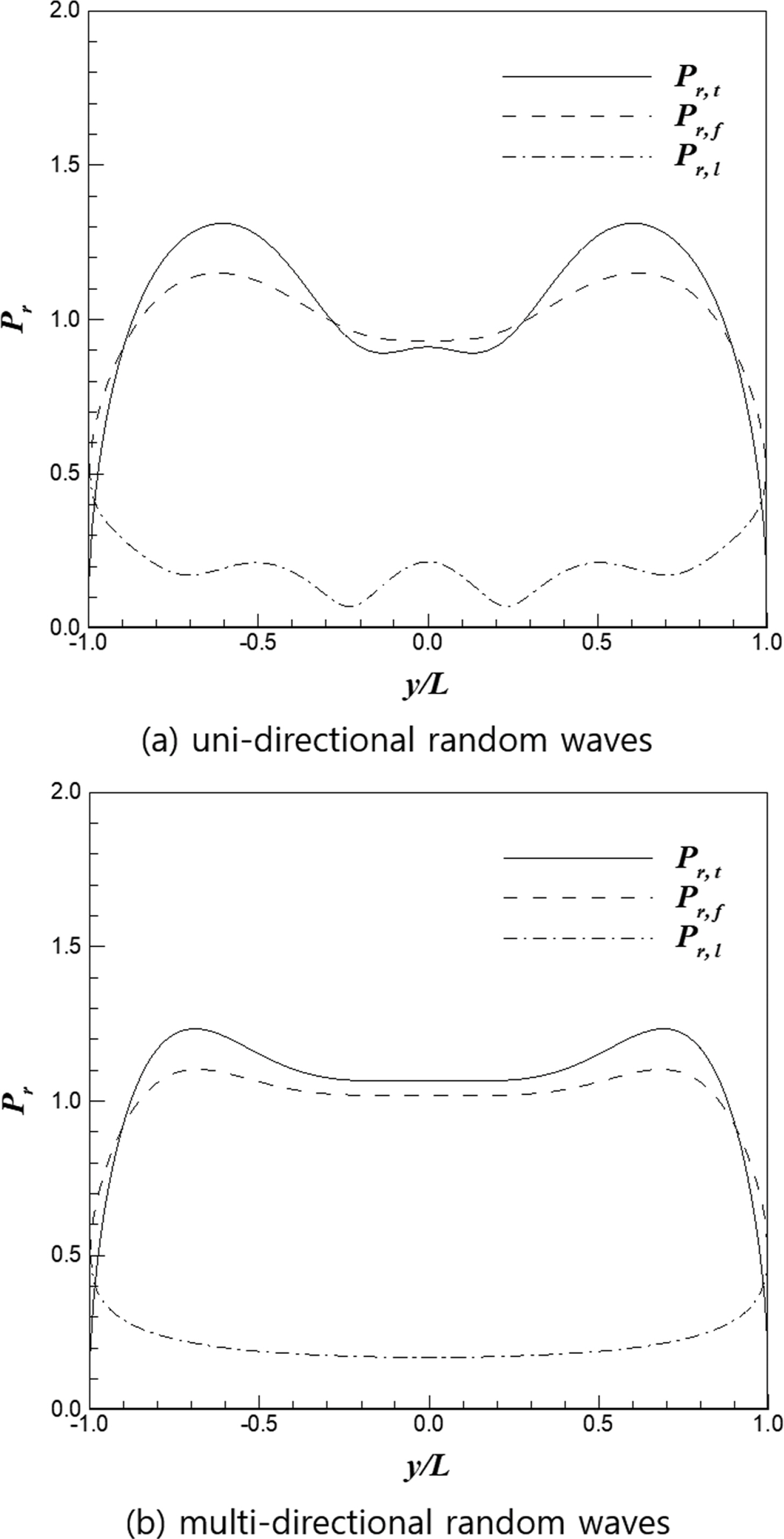
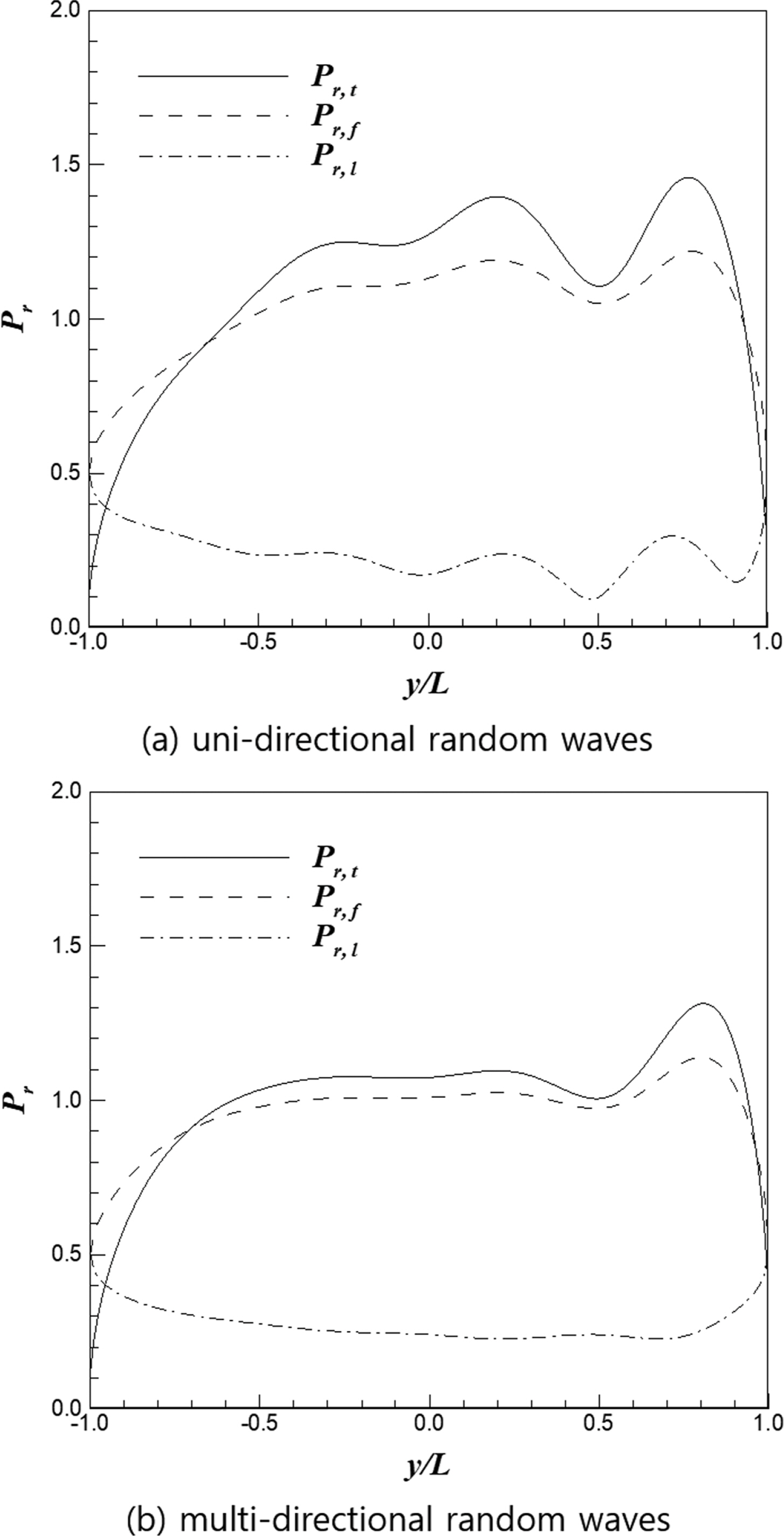
이안제에 작용하는 불규칙파의 파력에 대한 검토 조건으로 수심은 10 m, 입사파의 진폭은 1.0 m, 주기는 10초, 이안제의 상대길이(l/L)는 2.0, 첨두증진계수(γ)는 3.3이다. 수치계산을 위해 불규칙파의 주파수는 0.01 Hz에서 0.5 Hz까지 0.01 Hz 간격으로 분해하였으며, 파향(β)은 -90도에서 90도까지 1도 간격으로 분해하였다. 회절을 고려한 이안제에 작용하는 불규칙파의 상대 파력 분포는 Figs. 9~10에 나타내었다. 그림에서 실선은 이안제 전면 및 후면의 파력을 합성한 합성 파력, 파선은 이안제 전면에 작용하는 파력, 그리고 일점쇄선은 이안제 후면에 작용하는 파력을 각각 나타낸다. Fig. 9는 입사각이 0도인 경우이며, Fig. 9(a)는 일방향 불규칙파, Fig. 9(b)는 다방향 불규칙파의 결과이다. 일방향 불규칙파의 파력 분포는 규칙파의 파력 분포와 유사하게 나타났다(Fig. 7(a)). 일방향 불규칙파의 최대 합성 파력은 1.3, 다방향 불규칙파는 1.25로 각각 계산되었다. Fig. 10은 입사각이 45도인 경우의 결과로 일방향 불규칙파의 최대 합성 파력은 1.4, 다방향 불규칙파는 1.3으로 각각 계산되었다.
최대 합성파력이 이안제 전면에 작용하는 최대파력보다 크게 나타났다. 이는 Jung et al.(2021)이 반무한 방파제를 대상으로 검토한 결과와 같이 이안제 전면의 회절파와 후면의 회절파 사이에 180도 위상차가 있기 때문이다. 즉, 이안제 전면의 회절파의 파봉이 올 때 후면에서는 반드시 파곡이 위치하게 되며, 이는 이안제에 작용하는 파력이 더욱 증폭되는 현상을 야기한다.
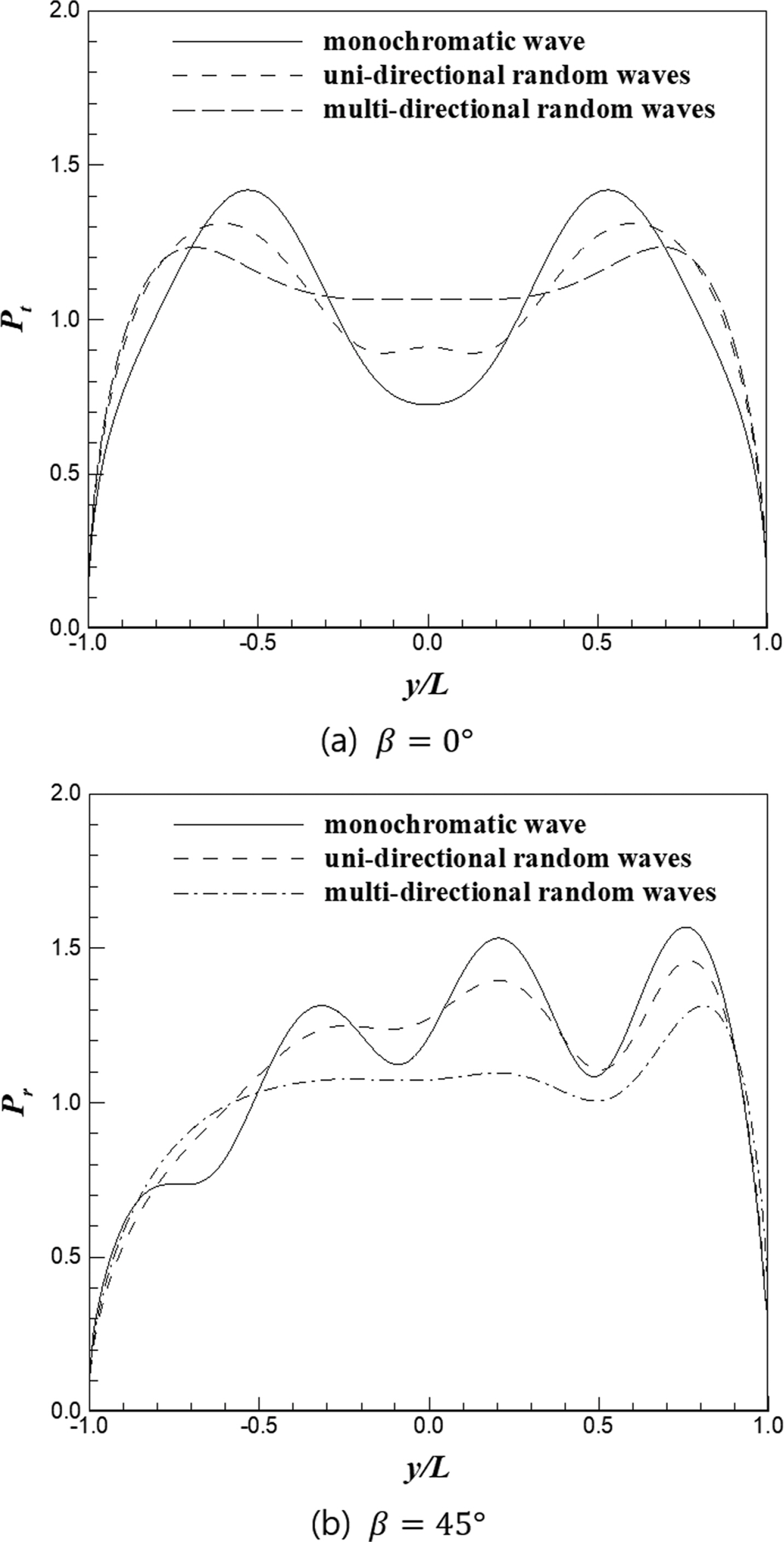
규칙파, 일방향 불규칙파 및 다방향 불규칙파의 합성 파력 분포는 Fig. 11에 나타내었다. 비교 결과 규칙파의 최대 합성 파력이 가장 크고, 일방향 불규칙파, 다방향 불규칙파 순으로 최대 합성 파력이 크게 계산되었다. 일방향 불규칙파의 경우 첨두 주기 이외의 다른 주파수 성분들 사이의 간섭, 다방향 불규칙파는 다양한 주파수 및 방향 성분들 사이의 간섭에 의해 파력이 상쇄되기 때문인 것으로 검토되었다.
파랑의 방향 비대칭성을 고려한 결과는 Fig. 12에 나타내 었다. 파랑이 수직으로 입사하는 경우에는 대칭인 경우보다 비대칭인 경우 파력이 더욱 크게 나타났다. 이안제는 y = 0인축을 기준으로 대칭이기 때문에 비대칭 계수가 0.3 및 -0.3 인 경우 결과가 y = 0인 축을 기준으로 거울 반전인 것으로 나타났다. 입사각이 45도인 경우에는 이안제에 수직인 방향의 성분이 우세한 μ = - 0.3인 경우 전반적으로 파력이 크게 계산되었다.
이안제에 주변에서 규칙파, 일방향 불규칙파 및 다방향 불규칙파 내습시 파력의 공간적인 분포에 대해 검토한 결과 회절파를 고려한 경우가 회절을 고려하지 않은 경우보다 50% 이상 파력이 큰 경우가 공통적으로 발생하였다. 그리고, 입사각에 따라 파력의 공간적인 분포가 크게 변화함을 확인하였다.
5. 결론
본 연구에서는 선형파 이론과 Penney and Price(1952)에 의해 제시된 반무한방파제 주변의 회절에 대한 해를 중첩하여 이안제 주변에 발생하는 회절에 관한 해를 제시하였다. 그리고, 이를 이용하여 이안제 전면과 후면, 그리고 전·후면에 작용하는 합성파력에 대한 해를 유도하였다. 규칙파, 일방향 불규칙파 및 다방향 불규칙파를 입사파랑으로 하여 이안제에 작용하는 파력에 대해 검토하였다.
이안제 주변의 파랑 변화에 대해 수치해석을 통해 검토하였다. 이안제 전면과 후면에서는 회절파와 중복파, 이안제 양쪽에서 회절한 회절파와 회절파 사이의 간섭에 의해 상대진 폭이 공간상에서 주기적으로 변하는 양상을 보였다. 회절을 고려하고 이안제의 상대길이가 5L 일 때, 이안제 전면에서 최대 진폭이 입사파랑 대비 2.48배에 이르는 것으로 나타났다.
이안제에 작용하는 파력에 대해서도 수치해석을 통해 검토하였다. 검토 결과 규칙파 내습시 이안제 전·후면의 파력을 모두 고려한 합성파력의 경우 회절을 고려하지 않았을 경우에 비해 최대 1.6배까지 파력이 증가하는 것으로 나타났다. 이는 Jung et al.(2021)이 반무한 방파제에 대해 회절효과를 고려하여 검토한 결과인 1.34배보다 큰 수치이다. 파랑이 비스듬히 입사하는 경우 이안제에 수직으로 입사하는 경우보다 최대파력이 크게 나타나는 경우가 나타났다. 이는 이안제를 설계할 때, 회절효과, 이안제 전·후면에 작용하는 파력, 파랑의 입사각을 반드시 고려해야 함을 의미한다.