요약선행연구에서는 3차원규칙파에 대해 olaFlow 수치모델을 적용하여 혼성방파제의 선단 주변에서 파랑특성 및 케이슨에 작용하는 파압특성을 검토하였다. 본 연구에서는 동일한 수치모델과 혼성방파제의 배치 및 형상을 적용하여 일방향불규칙파의 작용 하에 고천단의 마운드 상에 놓인 케이슨의 선단 주변에서 회절파의 발생과 배후역으로의 영향 및 케이슨에 작용하는 충격쇄파압을 포함한 파압의 공간적인 변동 등을 2차원 및 3차원적으로 검토한다. 또한, 수치해석으로부터 혼성방파제 주변에서 주파수스펙트럼, 평균유의파고, 평균수평유속 및 평균난류운동에너지의 변동특성도 면밀히 분석·검토한다. 이로부터 2차원수치해석에서는 발생되지 않았던 충격쇄파압이 3차원수치해석에서는 발생되는 경우가 나타나고, 충격쇄파압의 발생 시 경우에 따라 기존의 설계조건보다 매우 큰 파압이 정수면 근방의 케이슨의 전면 벽체에 작용되는 등의 중요한 결과를 얻을 수 있었다. 또한, 동일한 입사유의파랑에 대해 케이슨에 작용하는 파압분포가 방파제의 길이에 따라 변동하는 것을 확인할 수 있었으며, 이러한 변동은 크기에서 차이를 나타내지만, 3차원규칙파에 대한 선행연구의 경우와 유사한 특성을 갖는다.
AbstractIn the previous study, both the wave characteristics at the tip of composite breakwater and on caisson were investigated by applying olaFlow numerical model of three-dimensional regular waves. In this paper, the same numerical model and layout/shape of composite breakwater as applied the previous study under the action of one directional irregular waves were used to analyze two and three-dimensional spatial change of wave force including the impulsive breaking wave pressure applied to trunk of breakwater, the effect of rear region, and the occurrence of diffracted waves at the tip of caisson located on the high crested rubble mound. In addition, the frequency spectrum, mean significant wave height, mean horizontal velocity, and mean turbulent kinetic energy through the numerical analysis were studied. In conclusion, the larger wave pressure occurs at the front wall of caisson around the still water level than the original design conditions when it generates the shock-crushing wave pressure in three-dimensional analysis condition. Which was not occurred by two-dimensional analysis. Furthermore, it was confirmed that the wave pressure distribution at the caisson changes along the length of breakwater when the same significant incident wave was applied to the caisson. Although there is difference in magnitude, but its variation shows the similar tendency with the case of previous study.
1. 서 론혼성방파제의 케이슨 전면에 중복파가 형성되고, 직립부를 따른 중복파고에서 공간변동은 방파제에 작용하는 파압의 공간변동을 야기하고, 이러한 작용파압으로 혼성방파제의 케이슨에서 활동파괴가 발생되는 경우 케이슨의 항 내측 활동거리에서 차이를 나타낸다(Ito and Tanimoto, 1971). 이러한 현상을 Ito and Tanimoto(1971)는 방파제 선단으로부터 회절파의 영향으로 설명하였고, 이로 인한 피해를 사행피해(meandering damage)로 칭하였다. 해외에서 이러한 사행피해가 다수 보고되어 있고(Takahashi et al., 1993), 3차원규칙파에 관한 선행연구(Choi et al., 2020)에서도 지적한 바와 같이 최근 국내에서도 설계 내구년의 초과에 따른 노후화와 더불어 설계 당시에 예측하지 못한 이상파랑과 큰 충격파압의 작용으로 유사한 피해사례가 빈번히 발생되고 있는 것도 현실이다.
최근에는 혼성방파제를 포함한 구조물에 작용하는 파력과 구조물 주변에서 파동장의 변동특성을 수치적으로 접근하려는 연구들이 시도되고 있다. 이를 위하여 주로 혼상류에 대한 Navier-Stokes 운동방정식, VOF(Volume Of Fluid) 법에 의한 쇄파 및 난류 등을 고려할 수 있는 고정도의 3차원수치해석법이 개발되어 왔으며, 이를 적용한 수치연구로부터 직립부에 작용하는 충격력과 충격력에 의한 케이슨의 활동거리 등을 예측하고 있지만, 해석은 대부분 단면검토에 머물고 있고, 방파제 선단에서 회절파와 작용파력의 공간변동 등과 같은 3차원적인 접근은 거의 수행되지 않고 있다.
여기서, 3차원규칙파동장에서 회절파와 작용파력에 대한 수치연구로는 본 연구의 선행연구(Choi et al., 2020)를 들 수 있고, 선행연구에서는 혼성방파제의 케이슨에 충격쇄파력의 작용을 유도하기 위하여 고천단의 사석마운드 상에 케이슨이 설치된 혼성방파제를 고려하고, 3차원규칙파동장에 혼상류해석, 난류해석 및 쇄파해석이 가능한 olaFlow(Higuera et al., 2018) 모델을 적용하여 방파제 선단부 주변에서 회절파, 충격쇄파압을 포함한 파압의 변동, 평균수평유속 및 평균난류운동에너지의 변동특성을 면밀히 분석·검토하였다. 한편, 3차원불규칙파동장을 대상으로 한 수치연구로 Higuera et al. (2014)을 들 수 있지만, 이들은 3차원해석에서 소요되는 막대한 계산시간과 컴퓨터 용량을 줄이기 위하여 2차원과 3차원의 해석을 결합한 Hybrid 기법을 적용하였으며, 따라서 준 3차원해석법이라고도 할 수 있다. 이상과 같이 회절파와 작용파력에 대한 3차원파동장해석의 수치적인 연구사례는 매우 미미한 것으로 판단되며, 이의 이유로는 전술한 바와 같이 막대한 계산 시간과 경비 및 과대한 컴퓨터 용량 때문인 것으로 여겨진다.
본 연구에서는 선행연구(Choi et al., 2020)에서와 동일한 혼성방파제의 배치와 형상, 그리고 olaFlow(Higuera et al., 2018) 수치모델을 적용하고, 이로부터 일방향불규칙파동장에서 방파제 선단부 주변에서 회절파의 발생과 배후역으로의 영향 및 공간위치에 따른 케이슨의 항 내·외측에 작용하는 충격쇄파압을 포함한 파압의 변동특성 등을 2차원 및 3차원의 수치기법으로 해석하며, 동시에 기존의 설계공식(Goda, 2010; Takahashi et al., 1994)에 의한 결과와도 비교·검토한다. 또한, 구조물 주변에서의 스펙트럼의 변동특성과 혼성방파제 선단 주변에서 평균유의파고, 평균수평유속 및 평균난류운동에너지의 변동특성도 함께 면밀히 분석·검토한다.
2. 이론적인 배경본 연구에서 적용한 olaFlow(Higuera et al., 2018) 모델에 대한 이론적인 배경은 선행연구(Choi et al., 2020)에서 기술되었기 때문에 지면관계상 생략하며, 여기서는 불규칙파의 조파에 대해 기술한다. 불규칙파는 선형파이론으로부터 얻어진 각 성분파의 주파수에 순번을 붙인 무한급수의 합으로 고려된다. 조파에서는 조파지점에서 수면파형 η, 수평 및 연직유속 u 및 w의 시간변동이 필요하며, 이들은 각각 식(1)~(3)과 같이 주어진다.
여기서, εm은 Random 위상각, fm은 주파수, am은 진폭, km은 파수, M은 성분파의 수, h는 수심이다. 그리고, 연직좌표 z는 정수면에서 연직상방을 (+)로 취하며, 진폭 am은 다음의 식(4)로 정의된다.
여기서, ∆f는 주파수폭, S(f)는 파랑에너지밀도이며, 본 연구에서는 불규칙파의 스펙트럼으로 불규칙파를 모의하는 데에 널리 사용되는 다음 식(5)의 Modified Bretshneider-Mitsuyasu 스펙트럼(Goda, 1988)을 적용하였다.
여기서, H1/3은 입사유의파고, T1/3은 입사유의주기를 각각 나타낸다. 또한, 주파수 fm의 선택방법에는 주파수스펙트럼을 등구간으로 분할하는 방법과 각각의 성분파의 진폭이 같도록 등에너지로 분할하는 방법 등이 있다. 본 연구에서는 Modified Bretshneider-Mitsuyasu 스펙트럼(Goda, 1988)에 대해 등에너지로 스펙트럼을 분할할 수 있는 Goda(2000)에 의해 제안된 다음의 식(6)을 이용하여 주파수 fm을 선택하였다.
3. 혼성방파제의 수치해석결과3.1 불규칙파의 조파검증본 연구에서는 olaFlow(Higuera et al., 2018) 모델에 의한 불규칙파의 조파성능을 검증하기 위하여 후술하는 본 수치해석의 3차원수조의 제원과 각 케이스의 파제원을 사용하고, 구조물이 설치되지 않은 일정수심 h = 20 m의 수치파동수조에서 유의주기 T1/3 = 10 s, 15 s에 대해 유의파고 H1/3 = 2 m, 3 m를 목표로 각각 불규칙파를 600 s 동안 수치조파하였다. 적용한 스펙트럼은 전술한 Modified Bretschneider-Mitsuyasu 스펙트럼(Goda, 1988)이며, 150개의 성분파를 선형중첩하여 조파하였다. 그리고, 파랑의 반사 및 재반사가 해석영역의 파동장에 미치는 영향을 제거하기 위하여 수조 끝단에는 감쇠경계를 적용하였고, 조파판에는 조파와 감쇠가 동시에 작용하는 Pure active wave absorption 경계를 적용하였다. 이러한 조건 하에 조파판으로 부터 171 m 이격된 위치에서 계산된 각 케이스 별 조파개시 150 s 이후 정상상태의 불규칙파형과 주파수스펙트럼을 Fig. 1에 제시하며, 입력치인 표준스펙트럼(standard)도 병기되어있다. 여기서, 171 m 이격된 위치는 본 수치해석에서 혼성방파제의 케이슨 전면이 놓이는 위치이다. 표준스펙트럼과 측정스펙트럼을 비교하면 피크주파수에서 측정스펙트럼의 값이 약간 적은 결과를 나타내는 것을 볼 수 있다. 이러한 결과는 조파판에서 이격거리 171 m 거리에 걸쳐 전파되는 동안 발생되는 파에너지소산에 따른 결과이며, 이를 감안하면 전체적으로 타당한 결과를 나타내는 것으로 판단된다.
3.2 혼성방파제의 배치와 단면형상 및 수치해석 조건본 연구의 혼성방파제에 대한 3차원적인 배치 및 2차원의 단면형상을 Fig. 2에 나타내며, 이는 선행연구(Choi et al., 2020)에서도 기술한 바와 같이 쇄파충격파압을 유도하기 위하여 고천단의 사석마운드부를 적용한 Higuera et al.(2014)의 경우를 참조하였다. 그림에 나타내는 바와 같이 일정수심 h = 20 m에 x 방향으로 260 m, y 방향으로 170 m, 그리고 연직방향으로 35m의 크기를 갖는 3차원수치파동수조에 케이슨 길이 Lc = 90 m와 사석마운드 길이 Ls = 137 m의 혼성방파제가 설치되었으며, 이 때 개구폭 Lo = 33 m을 가진다. 단면은 사석마운드층, 중간피복층과 피복층(TTP)의 3개 층 및 케이슨으로 각각 구성되었으며, 피복층은 일반적인 경우보다 고천단이 적용되었고, 구조물의 수중부는 모두 1:2의 비탈경사를 가진다. 사석마운드는 높이 13 m, 공극률 ϕ = 0.45과 중앙 입경 D50 = 0.3 m로 구성되었고, 이의 다공성매질에 대한 저항계수는 Jensen et al.(2014)의 실험으로부터 α = 500과 β = 2.0가 적용되었다. 중간피복석은 두께 1.6 m, 공극률 ϕ = 0.5 과 중앙입경 D50 = 0.8 m로 구성되었고, 저항계수는 사석마운드와 동일하게 α = 500과 β = 2.0가 적용되었다. 또한, 피복층은 TTP의 난적으로 구성되었고, 두께 3.4 m, 공극률 ϕ = 0.55와 중앙입경 D50 = 1.7 m로 가정되었으며, Kondo and Takeda(1983)로부터 α = 1200, β = 1.7을 적용하였다. 그리고, 케이슨은 13 m의 높이를 가지며 불투과구조물로 고려되었다. 이상의 혼성방파제의 배치, 단면형상, 구성재료 및 물성치들은 연구에서 일관성을 유지하기 위하여 선행연구(Choi et al., 2020)에서와 동일하게 적용되었다.
격자크기는 수치해석의 계산효율을 위하여 수조의 조파지점에서 구조물이 설치되는 지점 앞 30 m까지는 ∆x = 1~0.5 m의 가변격자를, 그리고 ∆y = 0.5 m와 ∆z = 0.5 m의 격자크기를 적용하였으며, 이후 수조 끝단까지는 동일한 ∆x = ∆y = ∆z = 0.5 m의 정방격자를 적용하여 총 10,472,000개의 격자를 사용하였다. 그리고, 시간간격은 충격파압의 작용과 계산시간을 고려하여 ∆t = 0.05 s로 적용되었다. 수조의 저면과 양측 벽면 및 혼성방파제의 케이슨에는 불투과경계조건 및 Slip 조건이 적용되었고, 또한 수조의 조파위치와 끝단에는 감쇠경계가 적용되었다. 그리고, 난류는 LES 모델(Ghosal et al., 1995)로 해석되었다. 이러한 격자구성, 경계조건 및 적용난류 모델은 해석결과의 일관성을 유지하기 위하여 3차원규칙파에 대한 선행연구(Choi et al., 2020)에서와 동일하게 취해졌다.
Table 1은 본 수치해석에 적용한 불규칙파랑의 제원과 월파여부를 나타내며, 총 4 케이스에 대해 수치해석이 수행되었다. 규칙파를 적용한 선행연구(Choi et al., 2020)의 경우 월파가 발생하는 경우와 월파가 발생하지 않은 경우가 발생되었지만, 본 불규칙파의 연구에서는 모든 케이스에서 월파가 확인되었다. 이는 후술하는 수면변동에서 확인할 수 있다.
3.4 무차원평균유의파고
Fig. 4는 유의파고와 유의주기의 차이에 따른 무차원평균 유의파고
먼저, 동일한 유의주기에 대해 유의파고의 변화에 따른 결과를 살펴보면 구조물의 항 외측에서는 무차원평균유의파고의 변화가 대체적으로 크게 나타나지 않지만, 파가 집중되는 케이슨 전면과 파가 회절되어 항 내측으로 유입되는 선단부 근방에서는 등파고선의 변화가 다소 발생된다. 특히, 케이슨 전면에서 무차원평균유의파고가 중복파에 의해 1보다 큰 값이 나타나며, 최대 1.6까지 형성된다. 이러한 현상에 대해 유의파고의 차이에 따라서는 눈에 띄게 나타나지 않으며, 더불어 항 외측의 해역에서는 중복파의 마디와 배가 뚜렷이 형성되지 않는다. 이러한 결과는 불규칙파동장이므로 여러 주기 성분이 포함되어 배와 마디가 공간적으로 변동되기 때문이다. 반면, 선행연구(Choi et al., 2020)의 3차원규칙파에서는 하나의 주기성분으로 구성되기 때문에 배와 마디가 특정된 위치에 명확하게 나타나는 것을 확인할 수 있었다.
다음에, 동일한 유의파고에 대해 유의주기의 변화에 따른 결과를 살펴보면 유의주기가 길수록 선단부 근방에서 회절의 정도가 상대적으로 강하며, 파의 직진성이 상대적으로 약하게 나타나는 것을 확인할 수 있다. 또한, 회절된 파가 항 내측 케이슨 벽체를 따라 진행하면서 좌측 벽체 부근에서 중복 파동장이 약하게 형성되고, 유의주기가 긴 경우에 좌측 벽체로 회절되는 성분의 파가 상대적으로 크게 발생되는 것을 알 수 있다. 그리고, 케이슨 전면에서 중복파고는 유의주기가 긴 경우에 상대적으로 큰 무차원평균유의파고가 발생되는 반면, 케이슨 전면에서 케이슨을 따른 공간변화는 긴 유의주기의 경우가 상대적으로 작게 나타난다. 이러한 결과로부터 유의주기가 짧은 경우가 케이슨 벽체를 따른 작용파압의 공간변동이 크게 나타날 것으로 예상된다.
여기서, 반무한직립방파제의 전면에서 규칙파의 경우와 불규칙파의 경우를 대상으로 파고분포를 산정한 Ito and Tanimoto (1971)의 결과에 따르면 선단에서부터 방파제를 따라 파고가 사행변동을 나타내며, 내측으로 갈수록 그의 변동진폭이 감소되지만, 규칙파의 경우보다 불규칙파의 경우가 사행변동진폭이 작고, 동시에 내측으로 갈수록 그의 변동진폭이 급속이 감소되는 경향을 나타낸다. 이러한 Ito and Tanimoto(1971)의 결과와 3차원규칙파의 선행연구 및 일방향불규칙파의 현 연구결과와를 서로 비교하면 중복파고의 공간적인 사행변동을 나타내는 것은 동일하지만, Ito and Tanimoto(1971)의 결과보다 변동폭이 작다. 그리고, 케이슨을 따른 변동폭의 감소 경향은 동일하게 불규칙파가 규칙파의 경우보다 크게 나타나지만, 본 연구의 불규칙파에서는 상대적으로 변동이 매우 작게 나타나는 것을 알 수 있다. 이러한 결과는 고천단의 피복층에 의한 작은 반사율과 혼성방파제의 유한길이 때문인 것으로 판단된다.
3.5 각 지점에서의 스펙트럼의 변화
Fig. 5는 수면변동의 주파수스펙트럼 해석을 위한 파고계의 설치지점을 나타내며, Table 2는 해당지점의 좌표를 나타낸다. 조파지점으로부터 다소 이격된 Point 01, 피복층이 시작되는 Point 02와 Point 03, 케이슨 전면인 Point 04와 Point 05, 회절된 파가 통과하는 Point 06와 Point 07, 반사파와 회절파의 영향을 거의 받지 않는 Point 08, 항 내측의 Point 09~Point 12까지 총 12곳에서 주파수스펙트럼을 산출한 결과가 Fig. 6에 제시되었으며, 그림 중에는 입력치의 표준스펙트럼인 modified Bretschneider-Mitsuyasu spectrum (Goda, 1988)을 병기하였다. 여기서, 동일한 유의주기에 대해 유의파고가 변화된 경우에는 스펙트럼에서 값의 차이만 나타나고, 주파수에 따른 변동특성은 거의 동일하게 나타나는 것을 확인할 수 있다. 따라서, 여기서는 동일한 유의파고 H1/3 = 3 m에 대해 유의주기의 변동에 따른 스펙트럼의 변동특성을 서술한다.
먼저, 유의주기가 T1/3 = 10 s인 Fig. 6(a)의 경우 Point 01에서는 반사파의 영향이 거의 미치지 않아 측정스펙트럼은 표준스펙트럼과 거의 동일한 형상과 값을 나타내며, 피복층이 시작되는 Point 02에서는 피크주파수에서 표준스펙트럼보다 큰 값을 나타내지만, Point 03에서는 표준스펙트럼과 거의 동일한 주파수변동을 나타낸다. 이로부터 Point 02는 반사파의 영향을 크게 받고, 반면 Point 03는 회절파의 영향을 상대적으로 크게 받는다는 것을 알 수 있으며, 또한 표준치보다 측정치에서 피크주파수가 약간 고주파수대로 이동되는 것을 알 수 있다. 케이슨으로부터 반사파의 영향을 크게 받는 Point 04와 Point 05는 표준스펙트럼의 피크값보다 4배에 가까운 큰 스펙트럼의 피크값이 나타나며, 이는 전술한 무차원평균유의 파고에서 제시된 바와 같이 케이슨 전면에서 큰 중복파가 형성되기 때문이며, Point 04보다 Point 05에서 더 큰 스펙트럼값을 나타내는 것은 선단부 근방에서 더 큰 중복파고가 형성되기 때문이다. Point 06과 Point 07은 반사파와 회절파의 직접적인 영향을 받는 지점으로 표준스펙트럼보다는 약간 큰 값이 얻어지고, 케이슨 측벽에 가까운 Point 06이 Point 07 보다 피크값이 약간 크게 나타난다. Point 08에서는 반사파와 회절의 영향을 거의 받지 않기 때문에 스펙트럼이 표준보다 약간 적게 나타난다. 이는 입사파랑에너지의 해저마찰에 의한 감쇠결과로 판단된다. 구조물 배후영역 Point 09~Point 12에서는 매우 적은 측정스펙트럼값을 나타내며, 특히 Point 10과 Point 12에서는 쌍봉형의 스펙트럼을 나타내는 것을 확인할 수 있으며, 이러한 쌍봉형스펙트럼은 회절파와 월파에 의해 생성된 파가 중첩된 결과로 판단되며, 일반적으로 월파에 의해 생성된 파의 주기가 회절파보다 짧기 때문에 고주파수영역의 피크치는 월파에 의한 성분으로 판단된다.
다음으로, 유의주기가 T1/3 = 15 s인 Fig. 6(b)의 경우 Point 01에서는 케이슨에 다소 이격된 관계로 구조물에 의한 약한 반사파의 영향으로 스펙트럼피크값이 표준스펙트럼보다 약간 크게 나며, Point 02와 Point 03에서는 대략적으로 중복파의 마디에 위치하므로 측정피크값이 표준값보다 작게 나타남과 동시에, Point 02에서는 쌍봉형의 스펙트럼을 확인할 수 있다. Point 04와 Point 05에서는 대략적으로 중복파의 배에 위치하므로 측정값이 표준값보다 7배 정도 크게 나타나며, 유의주기 T1/3 = 10 s의 경우와는 달리 방파제 전면에서 케이슨을 따른 공간변화가 크게 없이 거의 동일한 크기의 높은 파봉이 나타나므로 Point 04와 Point 05에서 피크값이 거의 동일하게 나타난다. Point 06과 Point 07은 동일하게 회절파의 직접적인 영향을 받는 지점으로 유의주기 T1/3 = 10 s일 때와 동일한 형상을 나타낸다. 한편, 구조물의 배후영역인 Point 09~Point 12는 유의주기 T1/3 = 10 s일 때와 거의 유사한 스펙트럼값과 변동경향을 나타내며, 또한 Point 12에서 쌍봉형 스펙트럼을 나타내는 것을 알 수 있다.
3.6 평균수평유속해저 혹은 피복층의 표면에서부터 정수면까지 연직방향으로 3개 층으로 분할하고, 최저층에서 수평유속을 연직방향으로 시간평균한 평균수평유속의 공간분포를 나타낸 것이 Fig. 7이다. 여기서, 각 층의 연직높이는 동일하다.
Fig. 7을 살펴보면 케이슨 선단부에서 케이슨으로 향하는 수평유속의 수직성분이 크게 나타나며, 유의파고 및 유의주기에 관계없이 피복층 상에서 평균수평유속이 빨라지고, 동시에 항 내측에서 가장 빨라진다. 또한, 유의파고가 클수록, 그리고 유의주기가 길수록 피복층 상에서 평균수평유속이 빨라지는 경향을 나타낸다. 여기서, 전자의 유의파고에 대한 경향은 3차원규칙파동장에 대한 선행연구(Choi et al.,2020)의 경우와 동일하지만, 전체적으로 선단부의 피복층 상에서 평균수평유속은 불규칙파의 경우가 선행연구(Choi et al., 2020)의 규칙파보다 작은 값을 나타낸다.
한편, Fig. 8은 전술한 연직 3개 층의 전체를 연직방향으로 시간평균한 평균수평유속을 나타낸 것이다. 그림을 살펴보면 우측 방파제 선단부 근방에서는 전술한 최저층의 경우와 거의 동일한 경향을 나타내지만, 큰 유속이 분포하는 공간이 약간 확대되며, 항 내측에서 가장 빨라지는 Figs. 7(b)와 (d)와는 다르게 케이슨 측벽에서 빠른 유속분포가 고르게 나타나고, 유의파고가 크고, 유의주기가 길수록 집중도가 크게 나타난다. 또한, 전체적으로 선단부의 피복층 상에서 평균 수평유속은 불규칙파의 경우가 선행연구(Choi et al., 2020)의 규칙파보다 작은 값을 나타내는 것은 전술한 최저층에서의 경우와 동일하다.
3.7 평균난류운동에너지
Fig. 9는 전술한 Fig. 7의 평균수평유속에서와 같이 동일한 높이로 분할된 3개 층에서 최저층의 경우에 난류운동에너지를 연직방향으로 시간평균한 평균난류운동에너지의 공간분포를 나타낸 것이다. 이는
다음으로, Fig. 10은 3개 층 전체를 연직방향으로 시간평균한 평균난류운동에너지의 공간분포를 나타낸 것이다. 전술한 최저층에서 평균난류운동에너지의 공간분포와 같이 동일한 유의주기에 대해 유의파고가 증가하는 경우 혼성방파제 케이슨 전면과 선단부의 피복층 상에서 평균난류운동에너지가 상대적으로 증가하는 것은 동일하지만, 동일한 유의파고에 대해서는 유의주기가 증가하는 경우에 상대적으로 약간 감소하는 경향을 나타내며, 이는 선행연구(Choi et al., 2020)의 규칙파 결과와 동일한 경향이다. 또한, 값의 크기는 전체 층에 대한 경우가 전술한 최저층보다 다소 작은 값을 나타낸다. 그리고, 규칙파를 적용한 선행연구(Choi et al., 2020)와 비교하면 유의파고 및 유의주기의 변화에 따른 변동양상은 동일하지만, 선단부 피복층 상에서는 본 연구의 불규칙파의 경우가 규칙파보다는 훨씬 적은 값을 나타내는 것을 확인할 수 있다.
한편, 해저지반과 혼성방파제를 통합적으로 수치해석한 Ye et al.(2014)은 평균난류운동에너지가 이상과 같이 크게 집중되는 곳에서 구조물이 파괴되거나 사석이 이동될 가능이 높고, 결과적으로 쇄굴이 진행될 가능성이 높은 것으로 지적하고 있다. 또한, Kim and Lee(2017)은 선단부 우측의 피복석이 상대적으로 배후로 잘 이동되며, 파에 매우 취약하다는 것을 수리실험결과로부터 제시하고 있다. Fig. 11은 Kim and Lee(2017)에 의한 모식적으로 도시된 제두부 구간에 거치된 TTP의 파괴범위이다. 이러한 결과는 Figs. 9와 10의 평균난류운동에너지분포와 매우 유사하게 나타나며, 따라서 구조물의 파괴와 난류운동에너지는 매우 밀접한 관계가 있음을 확인할 수 있다. 여기서, 난류운동에너지의 공간분포로부터 해안·항만구조물에서 파괴위험성이 높은 공간위치를 판단할 수 있으므로 구조물의 설계 시에 검토될 수 있는 중요한 요소로 고려될 수 있다. 이러한 난류운동에너지의 시·공간변화를 평가하는 것은 실험실에서 계측으로는 어렵기 때문에 본 연구와 같은 고정도의 수치해석으로부터 구조물의 취약성을 규명하는 것도 하나의 유용한 방법인 것으로 판단된다.
3.8 케이슨에 작용하는 무차원최대파압
Fig. 12는 혼성방파제의 케이슨에 작용하는 최대수평파압과 양압의 공간분포를 검토하기 위하여 나타낸 구간별 단면의 위치이며, 총 5개의 단면위치에서 무차원최대수평파압 및 양압을 각각 추정하였다.
3.8.1 2차원해석(1) 무차원최대수평파압2차원 및 3차원해석에 의한 최대수평파압의 결과를 각각 비교·분석하기 위하여 2차원수치해석도 함께 수행하였다. 이 때, 모든 파랑조건과 구조물의 제원은 3차원의 경우와 동일하다. Fig. 13은 Fig. 2(b)에 제시된 2차원단면의 각 지점에서 유의파고와 유의주기의 변화에 따라 t = 0~600 s 사이에서 작용한 파압 중 가장 큰 최대파압 pmax를 ρgH1/3로 나눈 무차원최대 수평파압 pmax/ρgH1/3의 연직분포와 무차원최대양압 pu, max/ρgH1/3의 수평분포를 나타낸 것이며, 여기서 단면의 각 위치에서 작용파압의 위상차를 고려하지 않고 최대파압만을 고려한 것이다. 그림 중에는 olaFlow(Higuera et al., 2018) 모델에 의한 2차원수치해석결과뿐만 아니라 Goda(2010)의 파압 공식에 의한 결과와 Takahashi et al.(1994)에 의한 충격파압의 결과도 함께 제시되었다. 케이슨 전면에서 수평파압을 살펴보면 모든 케이스에서 Takahashi 등에 의한 충격파압이 Goda의 파압보다 큰 값을 나타내고, 유의주기가 짧은 Figs. 13(a)와 (b)의 경우를 제외하면 olaFlow 모델에 의해 수행된 2차원수치해석결과는 상대적으로 Goda의 파압에 근접한 결과를 나타내지만, 정수면 하에서는 Goda(2010) 및 Takahashi et al.(1994)의 결과가 olaFlow 모델에 의한 결과보다 매우 큰 값을 나타낸다. 이러한 결과는 Goda(2010) 및 Takahashi et al.(1994)에 의한 공식이 적용되는 혼성방파제의 경우 기초마운드 내 케이슨의 근입깊이가 얕기 때문에 케이슨 전면에 피복된 기초마운드의 영향이 고려되지 않았기 때문으로 판단되며, 따라서 본 연구와 같이 고천단의 기초마운드 내 케이슨의 근입깊이가 깊은 경우에는 그의 적용성을 신중히 검토할 필요가 있는 것으로 판단된다.
한편, 선행해석(Choi et al., 2020)에서도 기술한 바와 같이 수치해석결과가 실험치를 합리적으로 재현한다는 보편적인 가정에 근거하면 전술한 Figs. 13(c)와 (d)의 경우 Goda의 파압이 수치해석결과를 보다 타당하게 재현한다는 사실로부터 충격쇄파력계수 αI (Takahashi et al., 1994)와 파압계수 α2 (Goda, 2010)가 거의 동등한 값으로 추정되어 충격파압이 발생되지 않아야 한다. 그러나, 선행해석(Choi et al., 2020)의 규칙파랑에서와 같이 Goda의 파압보다 큰 충격파압이 발생되는 결과로부터 추론하면 충격압의 명확한 발생여부와 그 값의 정확한 예측에 불확실성이 크게 포함된다는 것을 본 연구의 불규칙파랑의 조건 하에서도 인지할 수 있다.
다음에, Figs. 13(a), (c), (d)에서는 2차원수치해석의 연직 분포에서 정수면 근방에서의 큰 파압(p1으로 칭한다)과 동등한 크기의 큰 파압(ps로 칭한다)이 정수면 하 피복층 상 약간 위에서 발생된다는 것을 확인할 수 있다. 또한, 수치해석 결과가 Fig. 13(a)의 경우 Goda파압보다 크고, Takahash충격파압보다는 작게 나타나는 반면, Fig. 13(b)의 경우 최대파압이 정수면보다 위에서 발생된다. 이러한 경향의 연직분포가 나타나는 것을 고찰하기 위하여 Fig. 14에 각 케이스 별 특정파압이 나타나는 시간대에서 수면형의 Snapshot과 특정파압의 발생지점을 함께 나타내었다. 그리고, 최대수평파압은 전술한 p1 혹은 ps가 선택적으로 주어진다.
먼저, Fig. 13(a)의 경우에 해당하는 케이슨 전면에서 파형의 전파과정을 나타낸 Fig. 14(a)를 살펴보면 시간의 경과와 케이슨의 직립부를 강타하면서 직립부 전면 상으로 처오름이 발생되는 과정을 가시적으로 확인할 수 있다. 이러한 과정에서 정수면 근방에서의 p1은 t = 147.75 s일 때 20 m 지점(그림에서 연직위치는 수로바닥을 0으로 규정되었으며, 따라서 정수면은 20 m로 주어진다)에서 나타나며, 그림으로부터 충격압의 작용에 의한 파압이 아니라는 것을 알 수 있다. 또한, 처오름에 의한 동압으로 정수면 하에서 t = 150 s일 때 18.8 m 지점에서 ps가 나타난다.
다음으로, Fig. 13(b)의 경우에 해당하는 Fig. 14(b)를 살펴보면 물입자의 수평속도가 위상속도보다 빨라 권파형의 쇄파가 나타나고, t = 147.5 s와 147.75 s 사이에서 수괴가 케이슨 직립부를 강타하며, 이에 따라 충격압이 발생됨과 동시에 파의 처오름이 일어나고, t = 147.75 s일 때 정수면보다 위인 20.9 m 지점에서 최대수평파압이 나타난다.
그리고, Fig. 13(c)의 경우에 해당하는 Fig. 14(c)에서는 파가 진행하면서 직립부 전면 상에서 처오름이 발생되고, 이어서 직립부 전면에서 파의 반사가 발생되어 반대방향으로 전파되는 과정을 확인할 수 있다. 이 과정에서 동압에 의한 p1이 t = 215.25 s일 때 20 m 지점에서 발생하고, 정수면 하에서 발생하는 ps는 t = 215.5 s일 때 18.7 m 지점에서 나타난다.
마지막으로, Fig. 13(d)의 경우에 해당하는 Fig. 14(d)를 살펴보면 Fig. 14(a)의 경우와 같이 파가 직립부를 강타한 후 파가 처오르고, 이어서 월파되는 상황을 볼 수 있다. 정수면에서의 p1은 파의 처오름 중인 t = 213.5 s일 때 20 m 지점에서 발생하고, 정수면 하에서 ps는 t = 215.5 s일 때 18.4 m 지점에서 발생되고 있다.
여기서, 케이슨 배후에서 제시된 수평파압은 2차원수치결과이며, 이는 월파된 파와 사석마운드부의 내부를 통한 전달파의 성분에 의한 결과이다. 이러한 파압은 케이슨 전면에서의 값에 비해 매우 적은 값을 나타내는 것을 알 수 있다.
(2) 무차원최대양압양압의 경우 항 내측에서 파가 존재하지 않는 것으로 고려되는 삼각형분포에 대한 Goda(2010)의 양압과 Takahashi et al.(1994)의 양압은 동일한 결과를 나타낸다. 이와 수치해석 결과와 비교하면 매우 큰 차이를 나타낸다. 이러한 차이는 Goda(2010)와 Takahashi et al.(1994)의 공식에서는 기초마운드부를 통한 전달파를 고려하지 않기 때문이다. 여기서, 수치 해석결과는 케이슨의 전면과 배면의 바닥에서 수평파압이 동시에 고려된 경향을 나타내며, 대략적으로 케이슨의 전면과 배면에서 큰 수평파압을 나타내는 경우가 큰 양압을 나타낸다. 케이슨 저면을 따른 수평분포는 비선형적으로 변화되며, 또한 유의주기가 길고, 유의파고가 큰 경우가 전반적으로 큰 양압을 나타내는 것을 알 수 있다. 이상의 결과는 선행연구(Choi et al., 2020)의 규칙파에 의한 결과와 동일한 경향을 나타낸다.
3.8.2 3차원해석(1) 무차원최대수평파압
Fig. 15는 Fig. 12에 제시된 케이슨 직립부의 전면 5곳의 단면위치(S.01~S.05)에서 유의파고와 유의주기의 변화에 따른 무차원최대수평파압 pmax/ρgH1/3의 연직분포와 무차원최대양압 pu, max/ρgH1/3의 수평분포를 나타낸 것으로, olaFlow (Higuera et al., 2018) 모델에 의한 3차원해석결과이다. 그림 중에는 전술한 2차원수치해석결과 및 Goda(2010)와 Takahashi et al.(1994)의 공식에 의한 결과도 병기한다.
먼저, 상대적으로 유의주기가 짧고, 유의파고가 작은 Fig. 15(a)의 경우를 살펴보면 전체적으로 Goda(2010)의 파압보다 크고, Takahashi et al.(1994)의 충격파압에 가까운 결과를 보이며, S.05에서 큰 최대수평파압을, 단면위치 S.01에서 가장 작은 값을 각각 나타낸다. 이러한 결과는 전술한 Figs. 4(a)와 (b)에 나타낸 것처럼 유의주기가 짧은 T1/3 = 10 s의 경우 선단부에서 발생하는 큰 파봉에 의해 S.05에서 큰 수평파압이 나타난다. 또한, Fig. 13(a)에 제시된 2차원의 경우보다 3차원이 케이슨의 단면위치에 따라 큰 파압 혹은 작은 파압의 분포를 나타나내만, 전체적으로 2차원의 경우가 3차원보다 상대적으로 작은 측의 값을 나타낸다. 여기서, S.05에서 3차원 수치결과가 전술한 Fig. 13(a)의 2차원수치결과보다 큰 수평파압이 작용되는 이유를 Fig. 16(a)에 나타낸 S.05에서 수위의 시간변동으로부터 고찰한다. Fig. 16(a)의 경우 파가 진행하면서 케이슨 전면에서 붕괴파형의 쇄파가 발생하고, 동시에 케이슨 전면을 강타한다. 이후에 파가 처오르는 과정에서 2차원수치결과보다 더 큰 최대수평파압이 t = 147.75 s일 때 정수면보다 약간 위인 20.3 m 지점에서 발생하게 된다. 이 파압은 Goda(2010)의 파압과 Takahashi et al.(1994)의 충격파압보다 더 큰 값을 나타낸다. 2차원해석에서 쇄파압이 발생되지 않은 반면, 3차원에서 쇄파와 동시에 충격파압이 발생되는 이유는 3차원의 경우에 선단부에 유의파고가 증폭되었기 때문이며, 유의파고의 크기가 충격파압에 미치는 영향에 대해서는 유의파고와 피복층 상 천단수심과의 비가 파라미터로 적용되는 Takahashi et al.(1994)의 충격파압산정식으로부터 알 수 있다. 이러한 3차원현상으로 파가 증폭되는 단면위치에서 파압을 정확히 평가하기 위해서는 3차원실험 혹은 본 연구와 같은 정밀한 3차원수치해석법으로 접근될 필요가 있다.
이어서, Fig. 15(b)의 경우를 살펴보면 전체적으로 Goda (2010)의 파압 및 Takahashi et al.(1994)의 충격파압보다 큰 파압분포를 나타내며, 정수면 근방에서는 S.05에서 큰 최대 수평파압을, 단면위치 S.01에서 가장 작은 값을 각각 나타낸다. 여기서, 정수면 근방에서 발생하는 최대파압은 전부 정수면보다 위에서 발생되는 것을 확인할 수 있다. Fig. 16(b)에 나타낸 S.05에서 수위의 시간변동으로부터 큰 최대수평파압의 발생에 대해 고찰한다. Fig. 16(b)로부터 직립부에 권파형의 쇄파가 충돌되고, t = 147.50 s일 때 정수면보다 약간 위인 20.2 m에 최대파압이 작용되는 것을 알 수 있다. 이후, 높은 처오름고를 나타낸다. 다음에, Fig. 16(c)에 나타낸 S.04에서 수위의 시간변동으로부터 최대수평파압이 정수면상 상대적으로 높은 위치에서 발생되는 현상을 고찰한다. Fig. 16(c)를 보면 Fig. 16(b)에서와 유사하게 권파형의 쇄파가 직립부를 강타하면서 직립부 상으로 약간의 처오름이 발생하는 순간 정수면보다 위인 21.4 m에서 최대수평파압이 작용한다.
다음에, Fig. 15(c)의 경우는 전체적으로 Goda(2010)의 파압에 근접한 값의 분포를 나타내고, 단면별 큰 차이가 없으며, 2차원수치해석과 유사한 파압분포를 나타낸다. 여기서, S.04에서 큰 최대수평파압을, 단면위치 S.01에서 가장 작은 값을 각각 나타낸다. Fig. 16(d)에 나타낸 S.04에서 수위의 시간변동으로부터 최대수평파압이 정수면(p1)과 정수면하(p3)에서 발생되는 현상을 검토한다. 이의 경우는 쇄파는 발생되지 않고, 직립부 상에 최대처오름이 발생하는 순간에 p1이 발생되고, 이후 반사파가 반대방향으로 전파되는 시각에 p3가 발생되는 것을 알 수 있다.
유의파고와 유의주기가 가장 큰 Fig. 15(d)의 경우는 Fig. 15(a)의 경우와 유사한 연직분포를 나타내지만, 정수면에서는 S.03의 경우에 최대치를 나타낸다. 이에 대해 Fig. 16(e)에 나타낸 S.03에서 수위의 시간변동으로부터 정수면(p1)과 정수면 하(p3)에서 발생되는 파압을 검토한다. 이의 경우는 전술한 바와 같이 쇄파는 발생되지 않고, 직립부 상에 최대처오름이 발생하는 순간에 정수면 상에서 p1이 발생되고, 이후 반사파가 반대방향으로 전파되는 시각에 정수면 하 18.7 m에서 p3가 발생되는 것을 알 수 있다.
4. 결 론본 연구에서는 3차원규칙파에 대한 선행연구(Choi et al., 2020)와 연구결과의 일관성을 유지하기 위하여 동일한 혼성 방파제의 배치, 단면형상, 수심, 구성재료, 물성치, 수조의 크기 및 수치모델을 적용하였으며, 동일한 olaFlow(Higuera et al., 2018) 수치모델을 이용하여 3차원수치파동수조에서 불규칙파를 조파하였다. 이로부터 유의파고와 유의주기 변화에 따라 구조물 주변에서 평균유의파고, 평균유속, 평균난류운동에너지의 각 공간분포 및 케이슨의 항 내·외측에 작용하는 2차원 및 3차원의 무차원최대수평파압 및 양압의 분포를 수치적으로 도출하여 공간위치에 따른 그의 변동특성 등을 기존의 2차원적인 파압추정공식(Goda, 2010)의 파압공식과 Takahashi et al.(1994)의 충격파압공식과 비교·분석하였다. 이로부터 다음과 같은 결론을 얻을 수 있었다.
(1) 무차원평균유의파고: 케이슨의 전면에서 무차원중복파고는 주기가 길수록, 동시에 파고가 작을수록 약간 높게 나타난다. 또한, 중복파고가 케이슨의 길이방향으로 위치에 따라 변동하며, 곳에 따라 파가 집중되는 현상이 나타나지만, 주기에 따라 상이하다. 방파제의 배후면에서는 유의주기가 긴 경우가 회절이 잘 발생되는 현상을 확인할 수 있다. 여기서, 3차원규칙파의 선행연구(Choi et al., 2020)와 비교하면 케이슨 전면에서 중복파고의 공간적인 사행분포는 불규칙파의 경우가 상대적으로 명확하지 않으며, 방파제 항 외측에서 중복파의 파고변화도 명확하지 않다.
(2) 평균수평유속: 선단부의 피복층 상 최저층 및 피복층 상 전체높이에 대한 각각의 평균수평유속은 굴절·회절의 영향으로 대부분이 케이슨에 수직에 가까운 방향으로 향하며, 유의파고 및 유의주기에 관계없이 피복층 상에서 평균수평유속이 빨라진다. 유의파고가 크고, 유의주기가 길수록 강하게 나타나지만, 유의주기의 변화에 따른 경향은 선행연구(Choi et al., 2020)와는 반대되는 경향을 나타낸다. 그리고, 케이슨 전면의 피복층 상에서 평균수평유속은 케이슨을 따른 흐름성분이 탁월하고, 내측으로 갈수록 케이슨에 수직한 성분이 탁월하게 나타난다. 3차원규칙파의 선행연구(Choi et al., 2020)와 비교하면 전체적으로 작은 평균수평유속을 나타낸다.
(3) 평균난류운동에너지: 선단부의 피복층 상 최저층 및 피복층 상 전체높이에 대한 각각의 평균난류운동에너지는 유의파고 및 유의주기에 관계없이 선단부의 피복층 상에서 강하게 집중되고, 또한 케이슨 전면의 피복층 상에서도 큰 값을 나타낸다. 이러한 결과는 선단부 근방에서 구조물의 파괴 및 피복재의 이동과 밀접한 연관을 가지는 것으로 판단된다. 선행연구(Choi et al., 2020)와 비교하면 유사한 경향을 나타내지만, 전체적으로 매우 작은 값의 평균난류운동에너지를 나타낸다.
(4) 무차원최대수평파압과 양압: 무차원최대수평파압은 케이슨의 공간위치에 따라 3차원의 경우가 2차원보다 큰 값을 나타내는 경우가 많고, 또한 케이슨의 공간위치에 따라 크게 변동한다. 2차원해석에서는 발생하지 않는 충격파압이 3차원 해석에서는 파의 공간집중에 의한 파고증폭현상으로 발생되는 경우가 있고, 이에 상대적으로 매우 큰 수평파압이 발생되는 단면위치도 있으며, 반면 Goda의 파압보다 작은 파압이 작용되는 단면위치도 있었다. 이러한 결과로부터 활동피해 시에 케이슨의 이동거리가 상이한 사행피해가 예상되며, 2차원의 단면적인 평가가 위험 측으로 될 소지가 존재한다. 무차원최대양압은 전체적으로 항 내측에서 회절파, 좌측 벽체로부터 반사파, 월류로 인한 파 및 기초마운드부를 통한 파에너지의 전달이 존재하기 때문에 케이슨의 배면에서 0의 값을 나타내지 않는다. 선행연구(Choi et al., 2020)와 비교하면 최대파의 값이 상이한 관계로 수평파압과 양압에 대해 상이한 분포와 경향을 나타내며, 직접적인 비교는 어렵다.
Fig. 1.Calculated wave profiles at wave source position and comparison of standard and calculated wave frequency spectra. 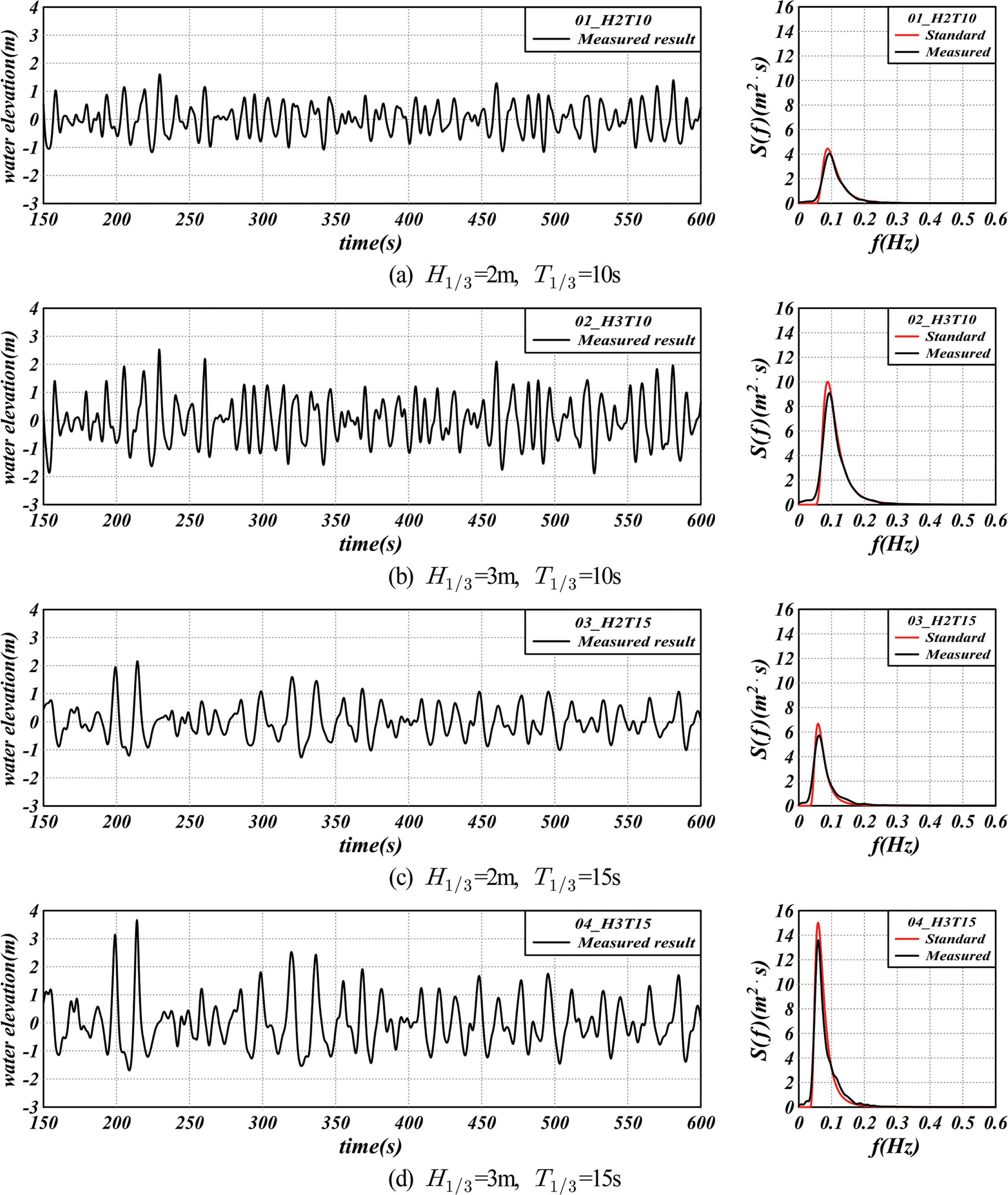
Fig. 4.Spatial distribution of simulated non-dimensional mean wave heights according to changes of wave height and period. 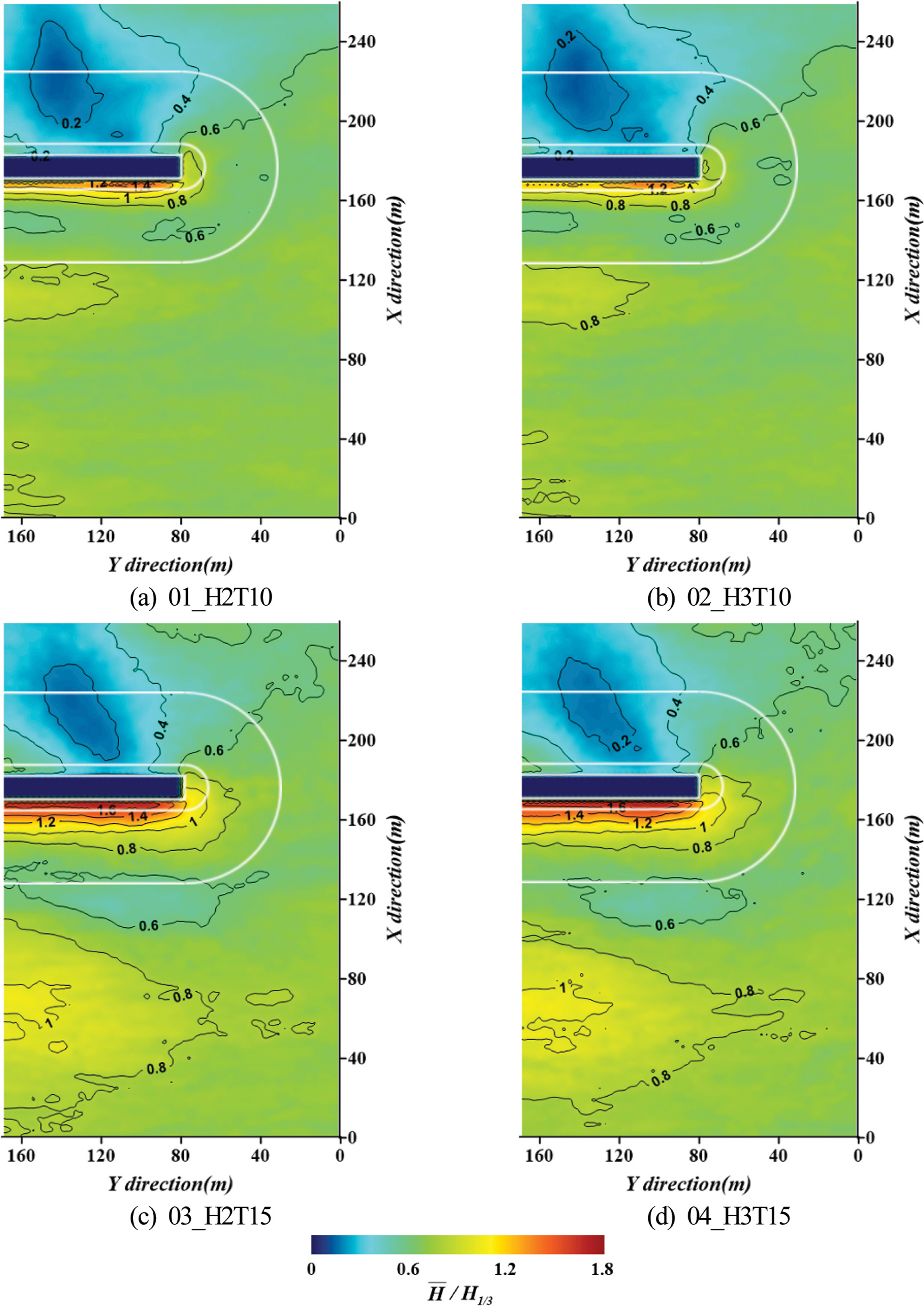
Fig. 7.Spatial distribution of mean horizontal velocities over the lowest layer according to changes of wave height and period. 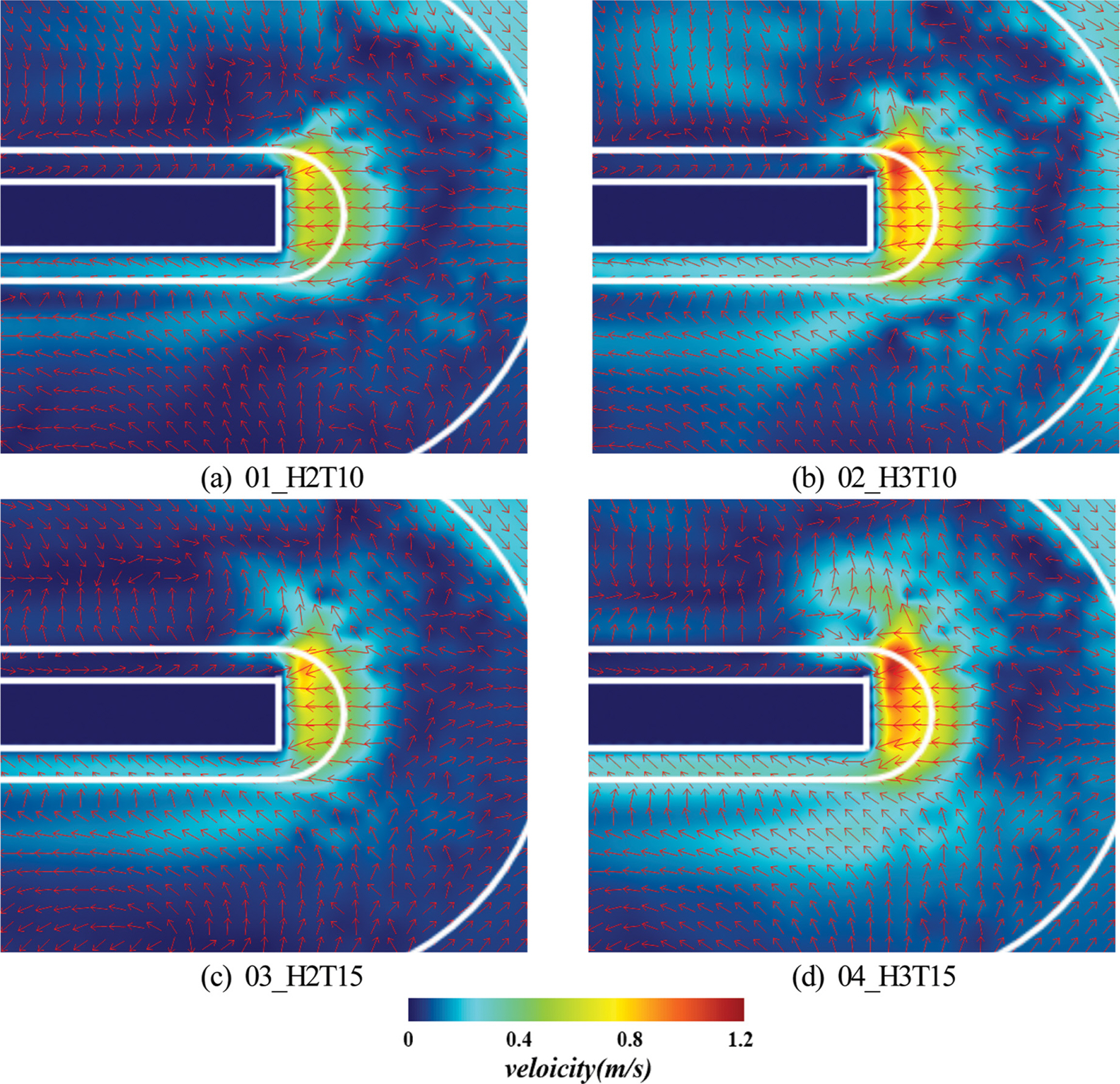
Fig. 8.Spatial distribution of mean horizontal velocities over the total layers according to changes of wave height and period. 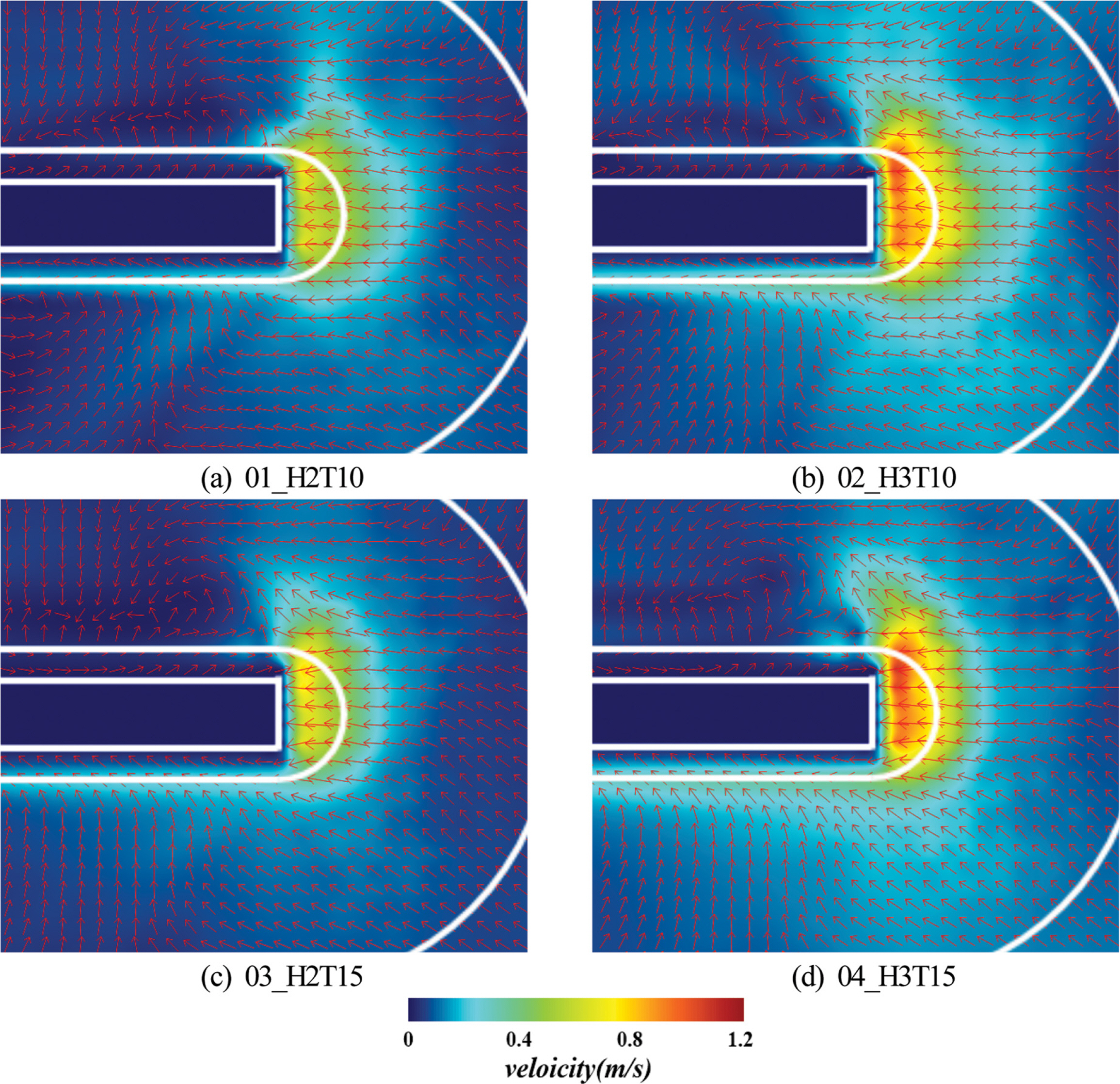
Fig. 9.Spatial distribution of mean turbulent kinetic energies over the lowest layer according to changes of wave height and period. 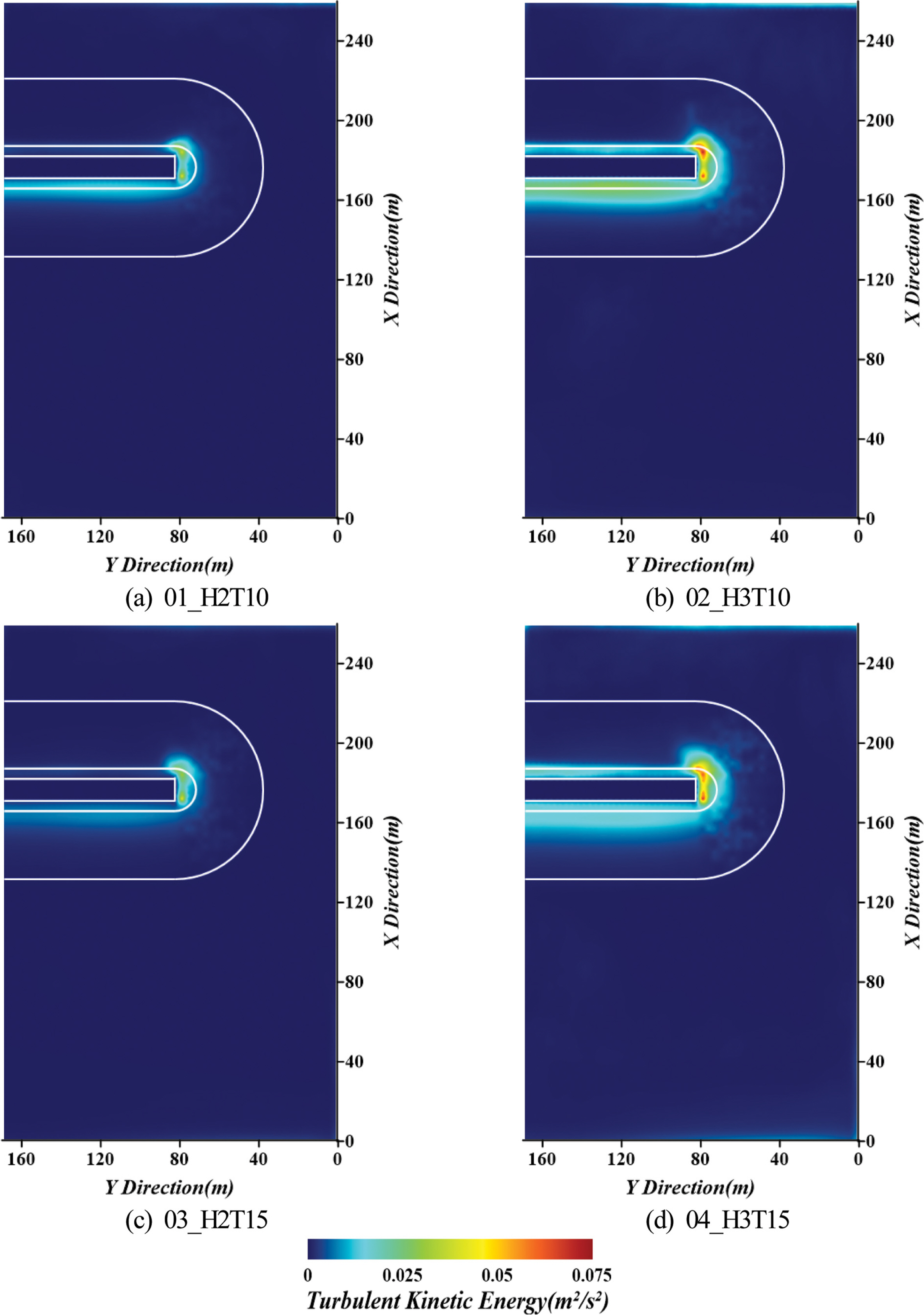
Fig. 10.Spatial distribution of mean turbulent kinetic energies over the total layers according to changes of wave height and period. 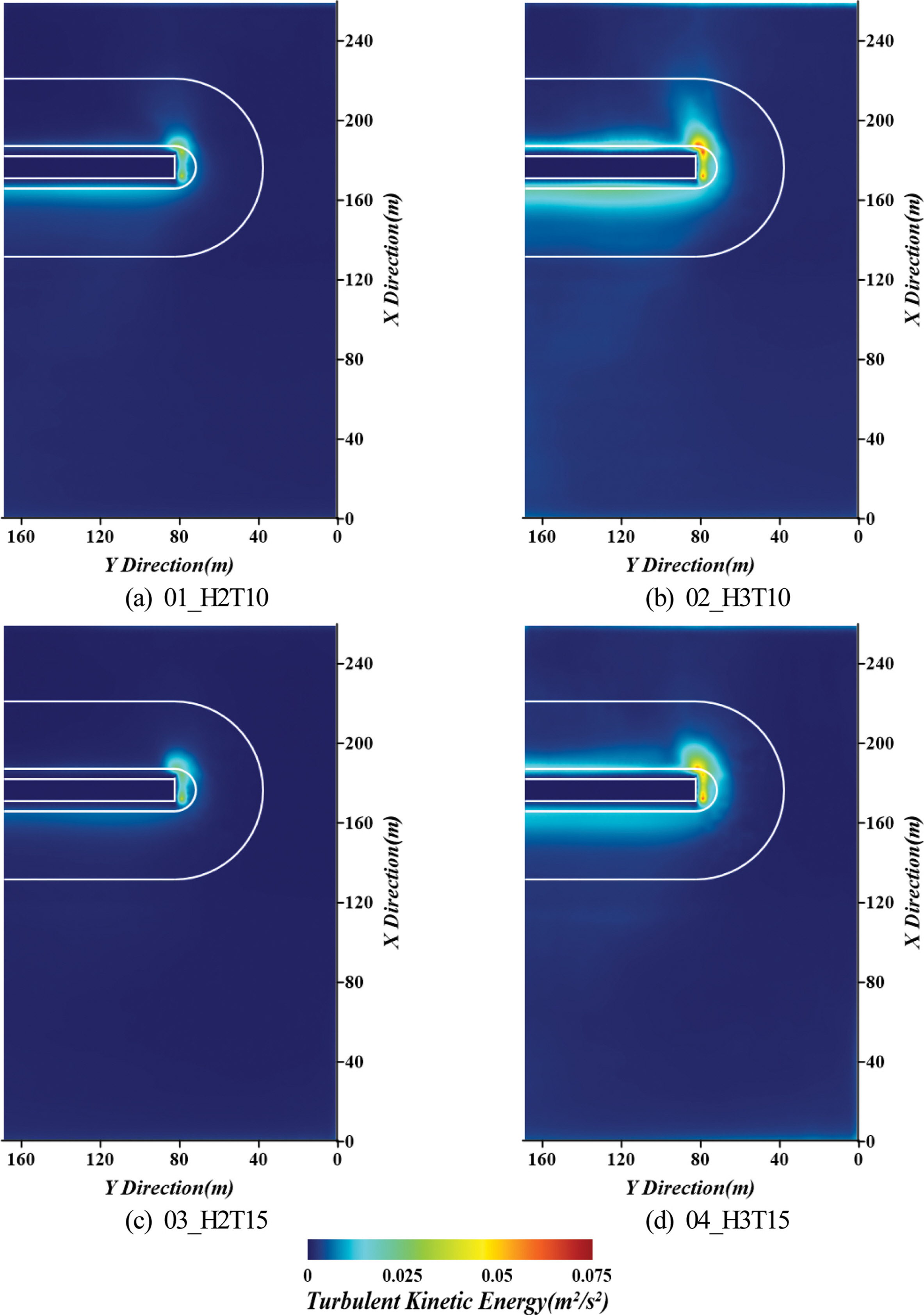
Fig. 12.Measuring points for maximum horizontal and uplift wave pressures acting on vertical caisson. 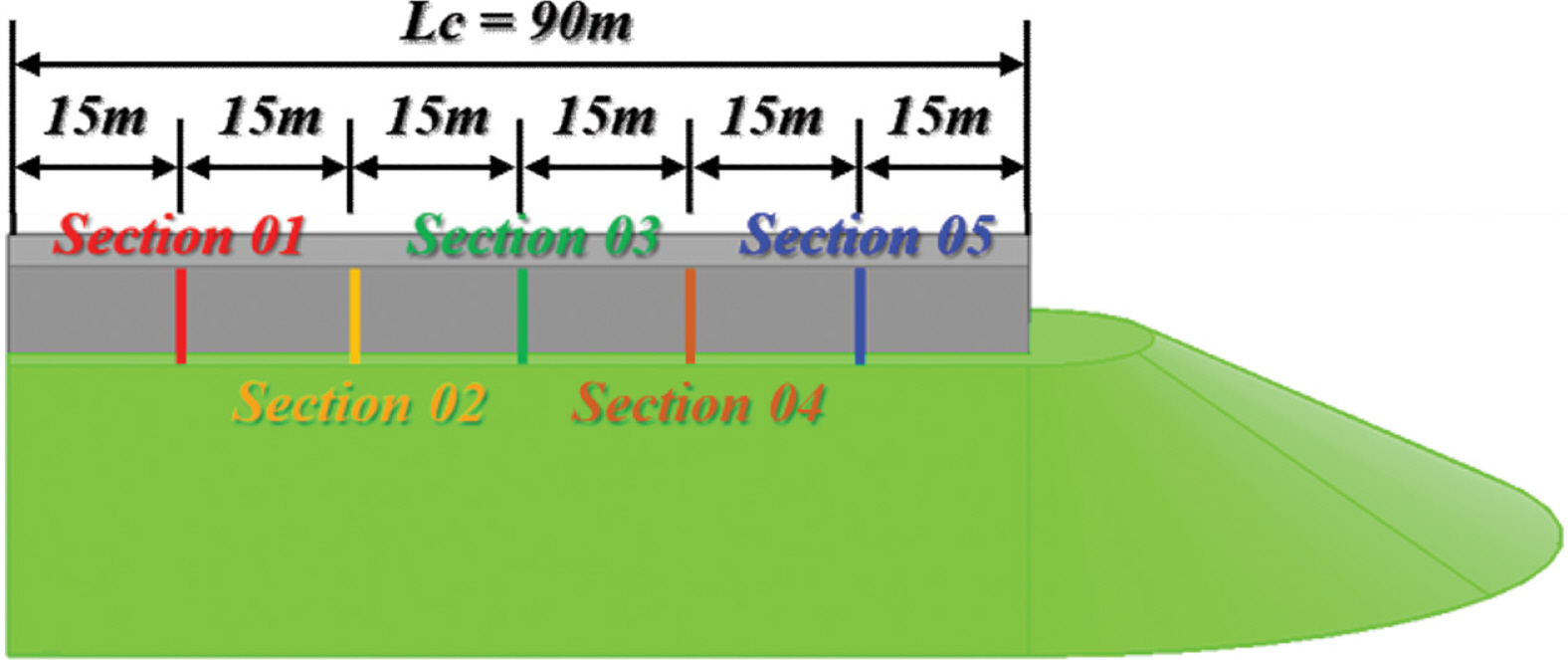
Fig. 13.Spatial distribution of non-dimensional maximum horizontal and uplift pressures acting on the caisson in case of two dimensional analysis. 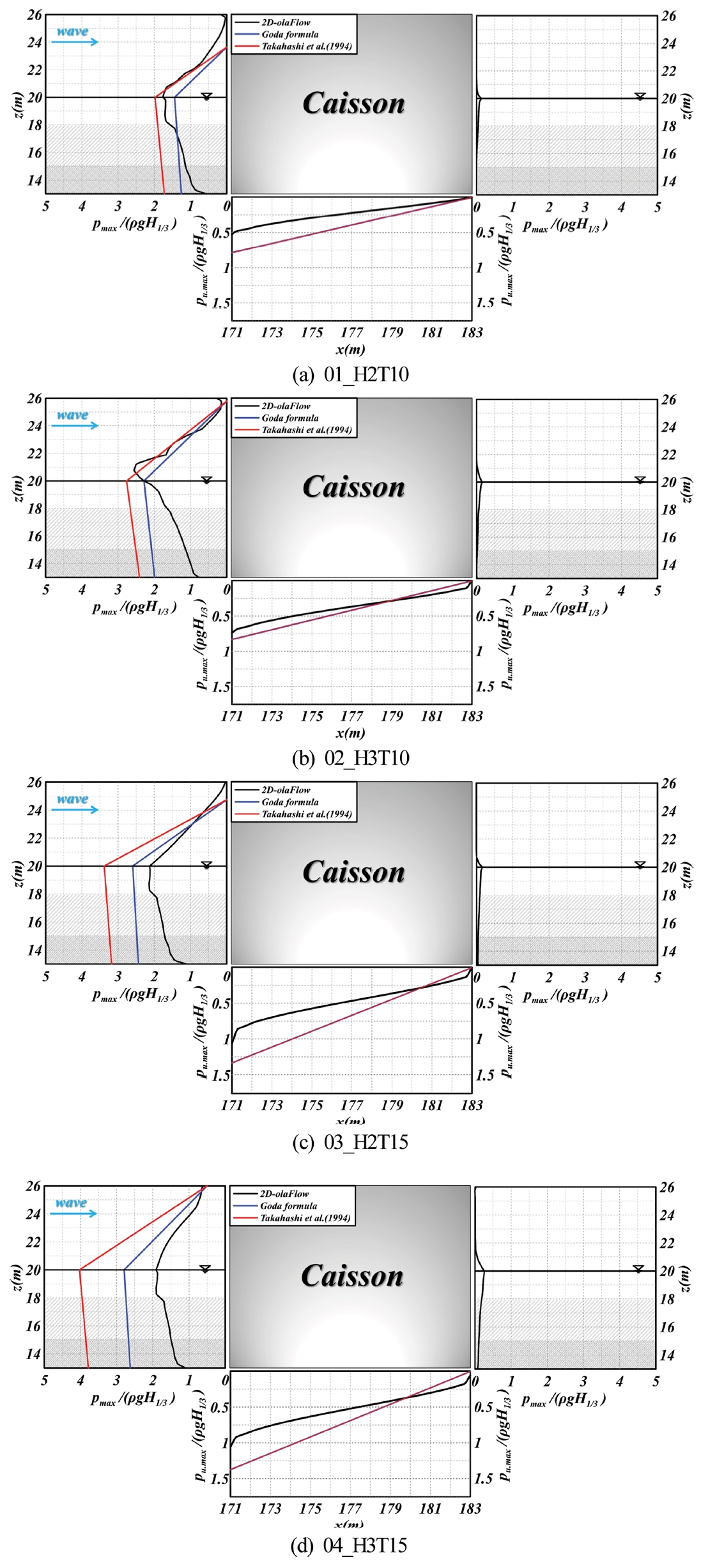
Fig. 15.Spatial distribution of non-dimensional maximum horizontal and uplift pressures on the caisson according to the changes of incident wave height and period. 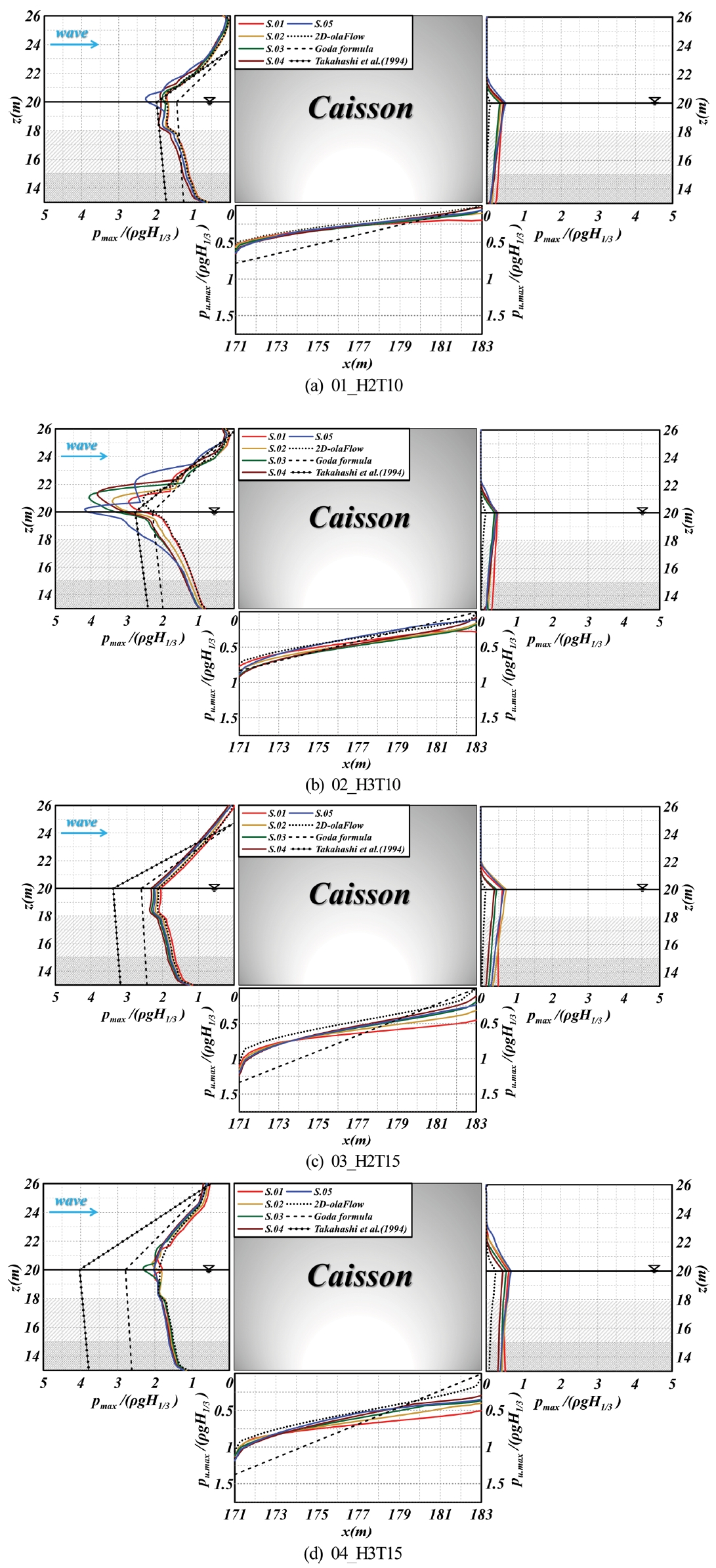
ReferencesChoi, G.H., Jun, J.H., Lee, K.H., Kim, D.S (2020). 3D-numerical simulation of wave pressure acting on caisson and wave characteristics near tip of composite breakwater, Journal of Korean Society of Coastal and Ocean Engineers, 32(3):180-201.
Ghosal, S., Lund, T., Moin, P., Akselvoll, K (1995). A dynamic localization model for large-eddy simulation of turbulent flows. J, Fluid Mechanics, 286, 229-255.
Goda, Y (1988). Statistical variability of sea state parameters as a function of wave spectrum, Coastal Engineering in Japan.
Goda, Y. (2000). Random seas and design of maritime structures. World Scientific Publishing, Singapore.
Goda, Y. (2010). Random seas and design of maritime structures. 3rd Edition. World Scientific Publishing, Co. Ltd, Singapore.
Higuera, P., Lara, J.L., Losada, I.J (2014). Three-dimensional interaction of waves and porous coastal structures using Open-FOAM. Part I: Formulation and validation, Coastal Engineering, 83, 243-258.
Higuera, P., Liu, P.F., Lin, C., Wong, W.Y., Kao, M.J (2018). Laboratory-scale swash flows generated by a non-breaking solitary wave on a steep slope, Journal of Fluid Mechanics, 847, 186-227.
Ito, Y, Tanimoto, K (1971). Meandering damage of composite type breakwater. Tech. Note of Port and Harbour Res, Inst, 112 (in Japanese)..
Jensen, B., Jacobsen, N.G., Christensen, E.D (2014). Investigations on the porous media equations and resistance coefficients for coastal structures, Coastal Engineering, 84, 56-72.
Kim, Y.T., Lee, J.I (2017). Hydraulic experiments on stable armor weight and covering range of round head of rubble-mound breakwater armored with tetrapods: Non-breaking conditions, Journal of Korean Society of Coastal and Ocean Engineers, 29(6):389-398 (in Korean)..
Kondo, S, Takeda, H. (1983). Wave dissipating structures. Morikita Publishing Co. Ltd, (in Japanese)..
Shimosako, K, Takahashi, T, Tanimoto, K (1994). Estimating the sliding distance of composite breakwaters due to wave forces inclusive of impulsive forces, ICCE, 1580-1594.
Takahashi, S., Tanimoto, K., Shimosako, K (1993). Experimental study of impulsive pressure on composite breakwaters-Fundamental feature of impulsive pressure and the impulsive pressure coefficient-, Rept. Port and Harbour Res. Inst, 31(5):33-72 (in Japanese)..
Takahashi, S, Tanimoto, K, Shimosako, K (1994). A proposal of impulsive pressure coefficient for design of composite breakwaters, Proceedings of the International Conference on Hydro-technical Engineering for Port and Harbour Construction, 489-504.
|
|