1. 서 론
해안의 특정 지점에 대한 지진해일 재해도 평가에는 결정론적(deterministic) 평가와 확률론적(probabilistic) 평가의 2가지가 있다. 결정론적 평가는 원자력발전소와 같이 극도의 안전을 요하는 시설물의 설계를 위해 물리적으로 발생 가능한 최대치, 즉 가능최대 지진해일(Probable Maximum Tsunami, PMT)을 가정하여 정한다. 가능최대 지진해일을 정하기 위해서도 주변 해역의 가능최대 지진을 가정하고, 이에 의한 지진해일고를 수치 계산하여 구한다. 따라서 결정론적 평가에서는 물리적으로 가능한 최대치 하나만을 구하므로 지진 자체의 물리 특성, 즉 발생위치, 지진규모, 단층 거동 특성 및 지진해일 전파와 처오름의 수치오차 등에 따르는 불확실성을 고려하지 못한다. 이러한 지진 자체 및 전파 수치모의에 따르는 불확실성을 고려하기 위해 확률론적 지진해일 분석을 수행한다. 확률론적 지진해일 평가는 확률론적 지진 재해도 평가(Probabilistic Seismic Hazard Analysis, PSHA)의 개념을 지진해일 분석에 도입한 것으로 대부분 지진 재해도 평가와 기법이 동일하나 지진파의 전파 과정 대신 지진에 의해 발생하는 지진해일 전파 수치모의를 수행하는 점만 다르다.
확률론적 지진해일 평가를 위해서는 비교적 자료가 풍부한 지진 기록을 분석하여 평균적인 지진원 위치와 규모, 발생빈도 및 단층 거동 특성 등을 정하고, 각 변수의 불확실성을 고려하여 평균치로부터의 편차를 가감하여 변동 범위의 상한과 하한을 설정한다. 이 변동 범위를 적당한 등급으로 세분하여 각각의 등급에 대한 가중치를 부여함으로써 주어진 변수의 불확실성을 고려하게 된다. 각 변수들에 대한 경우의 수가 많아지고 여러 변수들이 관련되면 검토해야 할 경우의 수는 기하급수적으로 증가하게 된다. 이러한 복잡한 과정을 체계적으로 관리하기 위해서는 로직트리의 작성이 필수적이다. 지진해일 재해도 평가를 위한 로직트리에 대한 연구 동향은 Jho et al.(2019)에 제시된 바 있다. Jho et al.(2019)은 로직트리 작성과 재해도 곡선 도출 방법에 대한 기초 연구로 동해 동연부의 대표 단층대 2곳에 국한하여 로직트리를 작성하였으나, 우리나라 남동해안에 영향을 주는 단층대는 동해 동연부에 6개 단층대가 존재하며, 류큐 트렌치에도 2개의 섭입대가 존재한다. 더구나 류큐 트렌치 섭입대에 대한 로직트리는 일본토목학회(Japan Society of Civil Engineers; JSCE) 보고서(2016)에서도 찾을 수 없어 독자적으로 작성해야 할 필요가 있다. 또한 파원역에서 멀리 떨어진 우리나라 동해안의 경우 단층 주향각의 작은 변화에도 관심 지역에서의 지진해일고가 크게 변할 수 있으므로 주향각에 대한 불확실성을 고려할 필요가 있다. 단층 주향각의 불확실성에 대한 로직트리 분기는 JSCE(2016)에서는 제시하고 있지 않으나 Sugino et al. (2015)의 연구 등에서 자주 채택되는 불확실성이며, 실제 단층파괴 전파과정을 시간의존형으로 복잡하게 해석하지 않고서도 종래의 동시파괴 모델을 이용하여 이를 쉽게 고려할 수 있는 방법의 개발이 필요하다.
본 연구에서는 한국 남동해안 중요 시설물 주변 해역에 대해 확률론적 지진해일 재해도 평가를 수행하기 위한 준비과정으로 이 해역에서 지진해일을 유발하는 모든 단층대 즉 동해 동연부 및 류큐 트렌치 단층대에서 발생하는 해저 지진 발생 특성과 이들 지진원으로부터 고리 부지 해역으로의 지진 해일 전파 과정을 파악하고, 이로부터 지진발생 및 전파 과정에 내재하는 불확실성을 도출하여 로직트리를 작성한다.
2. 로직트리 구성요소
확률론적 지진해일 평가를 위한 로직트리 구성요소에는 초기파형 결정을 위한 지진 및 단층 관련 정보(우연적 불확실성)와 수치모의로부터 결정된 최대 해일고의 확률분포 관련 정보(인식론적 불확실성)로 대별된다. 지진 및 단층관련 정보에는 지진원 위치, 지진 규모, 지진 발생 빈도, 단층 길이, 단층 폭, 주향각, 경사각, 활동각, 단층변위, 단층변위 분포(asperity) 등이 있고, 지진해일고 확률분포 관련 정보에는 표준편차와 타절범위 등이 있다
2.1 지진원 위치
우리나라 남동해안에 위치하는 고리 원자력발전소를 예로 들면 동해 동연부와 일본의 류큐 트렌치에서 발생하는 지진 해일의 영향을 주로 받게 된다.
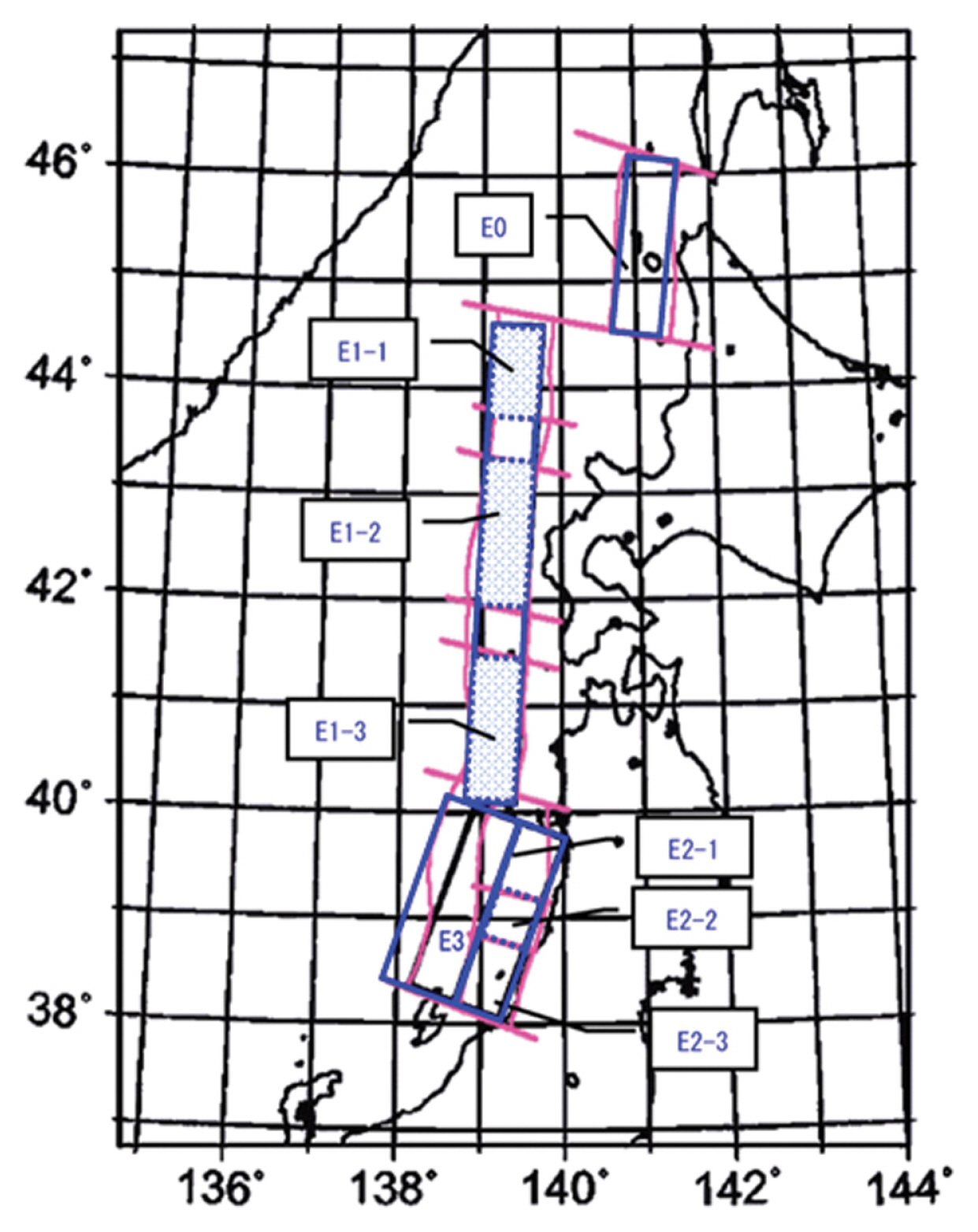
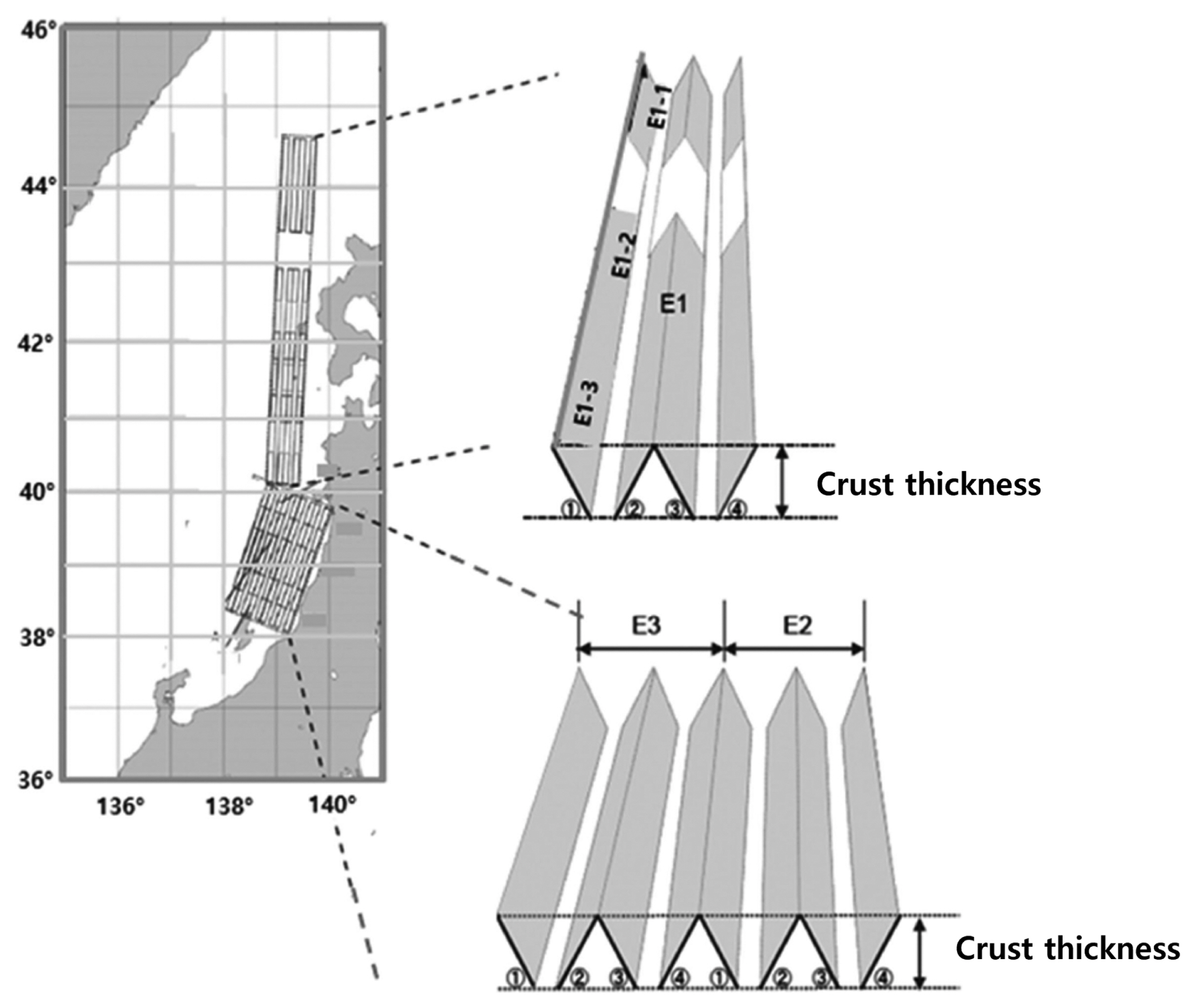
동해 동연부의 해저 활단층 조사 결과에 의하면 유라시아판과 북아메리카 판의 경계를 따라 남북으로 길게 발달된 단층대가 존재한다. 동해 동연부 단층대는 일본토목학회(JSCE, 2016)에 의하면 8개의 세그먼트(Fig. 1의 E0, E1-1, E1-2, E1-3, E2-1, E2-2, E2-3, E3)로 분할되어 있으며, 각 세그먼트에서 발생하는 지진은 서로 독립적으로 발생하는 것으로 판단되고 있다. 이들 중 E0, E1, E2와 E3 세그먼트는 독립적으로 거동하는 것을 원칙으로 하나 지진발생의 불확실성 고려 차원에서 여러 세그먼트가 분리되어 있지 않고 일체로 거동할 가능성도 로직트리에 반영한다. JSCE(2016)에 의하면 E2 세그먼트는 E2-1, E2-2, E2-3의 3개 세그먼트로 분류 가능하다. 그러나 E2의 전체 세그먼트 길이가 다른 단층대의 세그먼트 길이와 비슷하여 하나의 세그먼트로서 일체로 거동하는 것으로 평가할 수 있다.
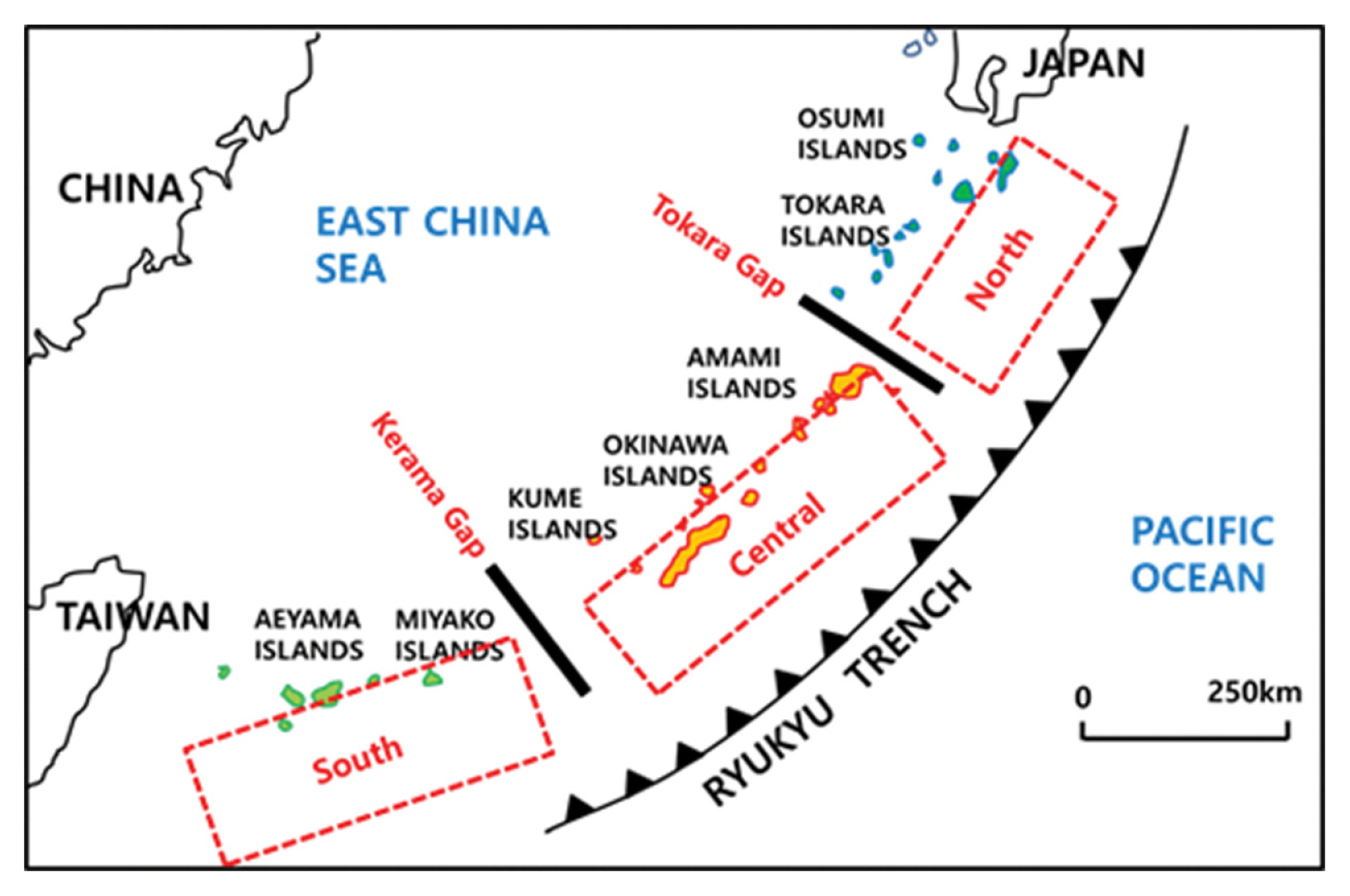
한편 류큐 트렌치는 필리핀해 판이 유라시아 판의 하부로 섭입되는 곳으로 Fig. 2에 보인 바와 같이 토카라 불연속 구간(Tokara Gap)과 케라마 불연속 구간(Kerama Gap) 등 2개의 불연속 구간에 의해 북부, 중부 및 남부의 3개 세그먼트로 분할된다.
이중 남부의 세그먼트에서 발생한 지진해일은 주 에너지가 동중국해의 해저지형의 영향으로 굴절되어 중국의 남부 해안으로 집중되므로 우리나라 남해안에 영향을 거의 미치지 않아 분석에서 제외하고, 중부 세그먼트와 북부 세그먼트 2개만을 고려한다. 이 2개 세그먼트도 동해 동연부 세그먼트와 같이 각각 독립적으로 지진이 발생하는 것으로 간주하나, 2개의 세그먼트가 일체로 거동하는 경우도 고려한다. 따라서 우리나라 남동해역인 고리 및 새울 원자력발전소 부지 해역에 영향을 주는 지진원은 동해 동연부의 E0, E1-1, E1-2, E1-3, E2 및 E3의 6개 세그먼트이며, 류큐 트렌치에 속한 지진원은 북부와 중부의 2개 세그먼트이다.
2.2 지진규모 및 발생빈도
지진원이 정해지면 지진원에서 발생가능한 지진의 규모와 발생빈도를 정한다. 지진의 규모와 발생빈도는 역사적 및 계기지진의 기록을 분석하고 전문가들의 의견을 종합하여 결정하며, 불확실성을 고려할 수 있도록 한다.
2.2.1 동해 동연부
과거 동해 동연부, 즉 일본 서안 영역에서 발생한 지진들에 대한 분석을 수행한다. 현재 기록으로 남겨진 동해 동연 부과거 지진 자료들은 길게는 1,000년 이상의 자료가 존재한다. 이 자료 중 1900년 이후의 지진기록은 계기지진이며, 그 이전 자료는 모두 역사기록이나 지층탐사에 의한 추정치로서 중소 규모의 지진기록이 누락되어 있다. 1900년 이후의 계기지진 기록도 1960년 이전 자료는 소규모의 지진이 결측되어 있는 경우가 많다.
이러한 지진규모에 대한 불확실성은 확률론적 지진해일 평가에서 로직트리 분기로 고려된다. Table 1은 동해 동연부의 6개 세그먼트에서 발생했거나 발생 가능성이 있는 지진 단층의 특성을 보여준다.
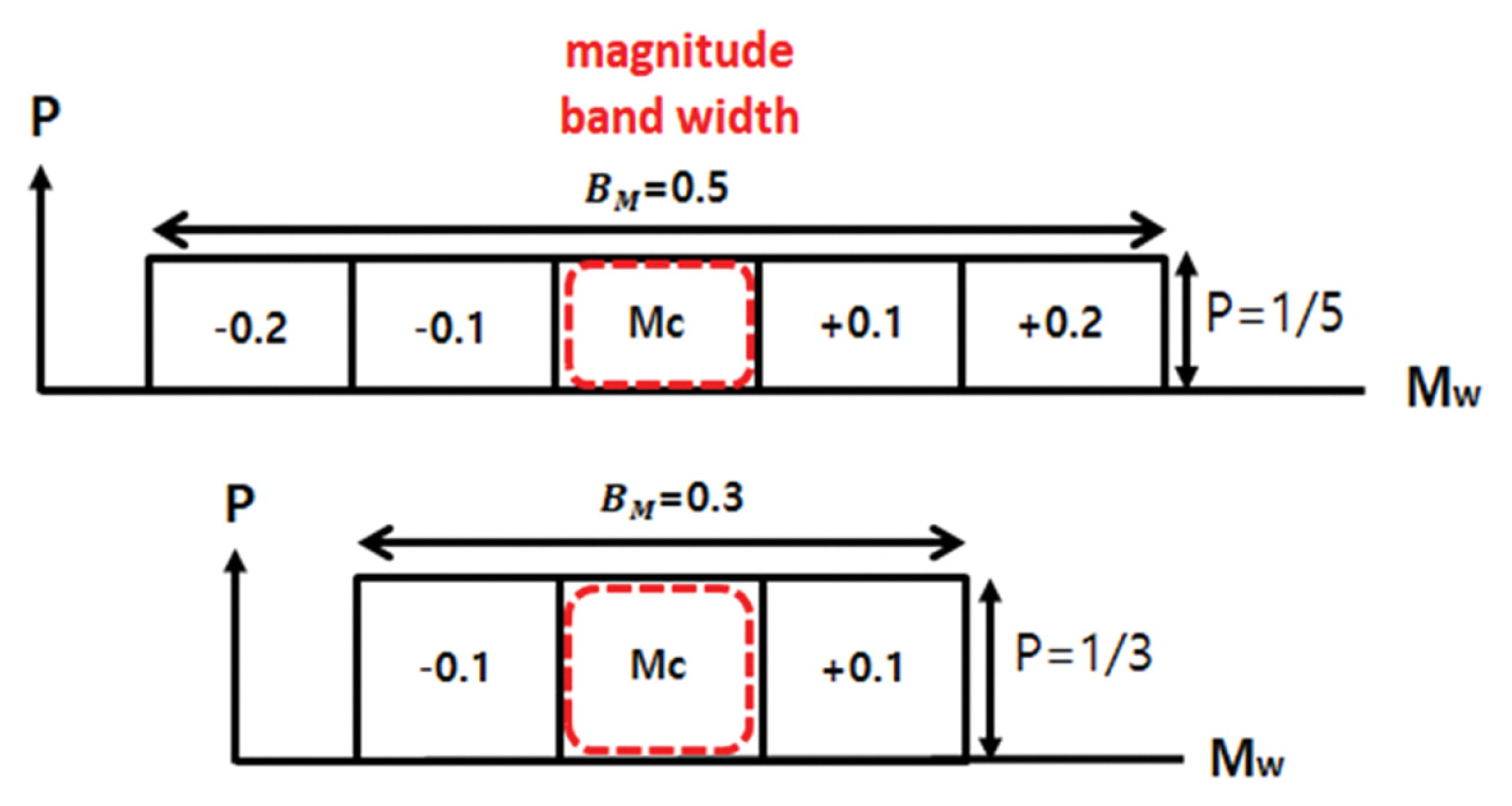
지진규모에 대한 로직트리는 주어진 지진규모에 불확실성을 고려하기 위한 규모변화폭 BM을 부여한다. Fig. 3에 보인 바와 같이 어떤 지진원의 지진규모가 Mw로 주어진 경우 주어진 지진규모 Mw보다 크거나 작은 규모를 고려하기 위해 주어진 Mw를 중앙치 Mc로 놓고 다양한 규모변화폭에 대해 검토하는 바, BM은 0.5와 0.3이 주로 이용된다. 실제 계산은 각각의 규모에 대해 지진해일고 추정 분기들을 고려하여 초과 확률분포를 계산한 다음 각각의 규모에 부여된 발생확률을 곱하여 합산함으로써 단일 초과확률분포를 구한다. 이상과 같은 과거 지진 발생 현황에 근거하여 각각의 지진 단층대에 대한 지진규모 및 재현기간에 대한 로직트리 분기를 설정하였으며, Table 1에 제시된 각 단층대의 지진 최대규모, 재현기간을 근거로 구성하였다. 또한, JSCE(2016)에서 제안된 바와 같이 각 단층대의 지진규모는 5개의 분기로 나누었으며, 재현기간은 JSCE(2011)에서 제시한 바와 같이 3개의 분기로 나누어 고려하였다.
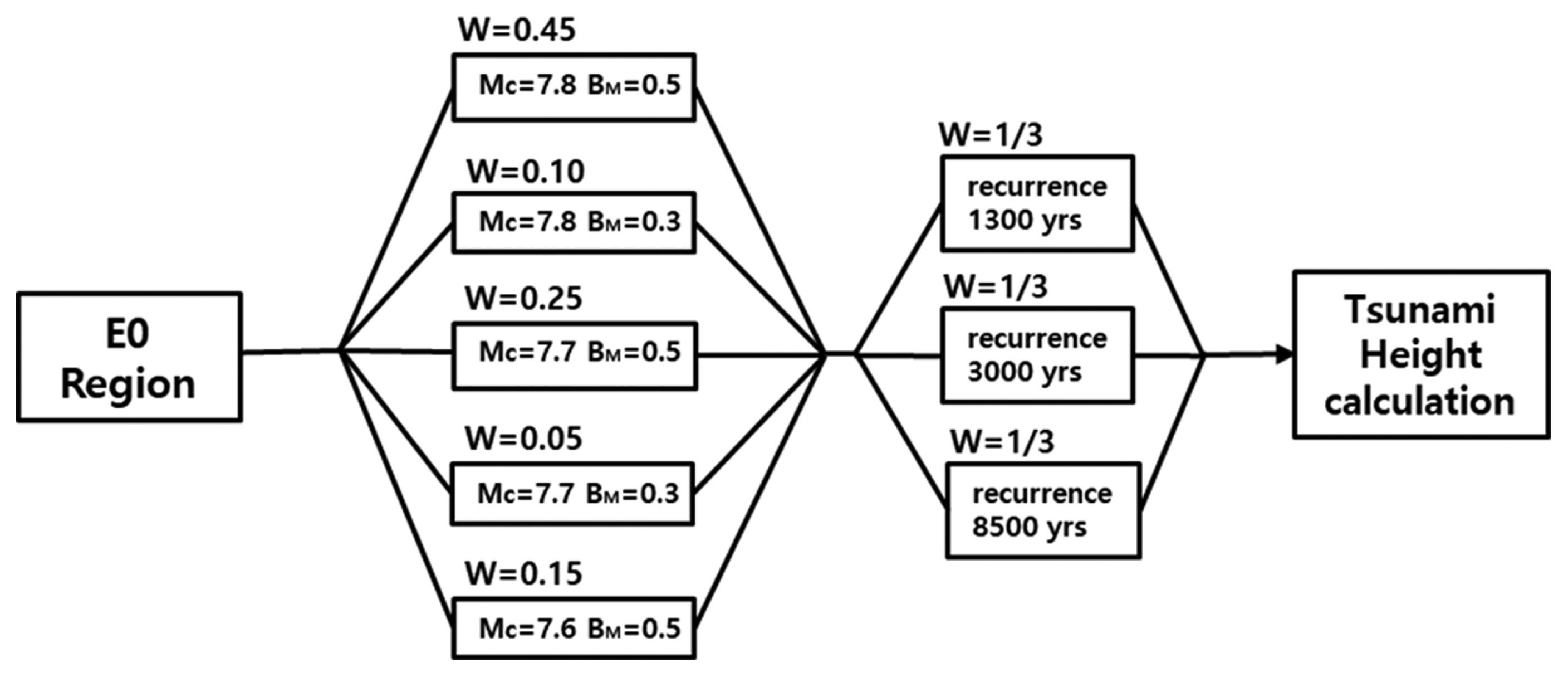
Fig. 4는 동해 동연부의 최북단인 E0 세그먼트에 대해 JSCE(2011)가 추천하는 로직트리이다. 그림에서 w는 각 로직트리 분기에 부여된 가중치(weight)이며, 지진규모 5개 분기의 가중치는 JSCE(2008)에서 많은 전문가 인터뷰를 통해 얻어진 것이다. 동일한 분기에서 가중치의 합은 항상 1이다. 발생빈도, 즉 지진의 재현기간은 E0 세그먼트에 대해서는 Table 1에 보인 바와 같이 범위가 최소 1,300년에서 최대 8,500년이다. 이 범위를 3가지 재현기간(1,300년, 3,000년 및 8,500년)을 명시적으로 제공하고 있다. E0 세그먼트의 재현기간 분기의 가중치는 각각 1/3을 추천하고 있다.
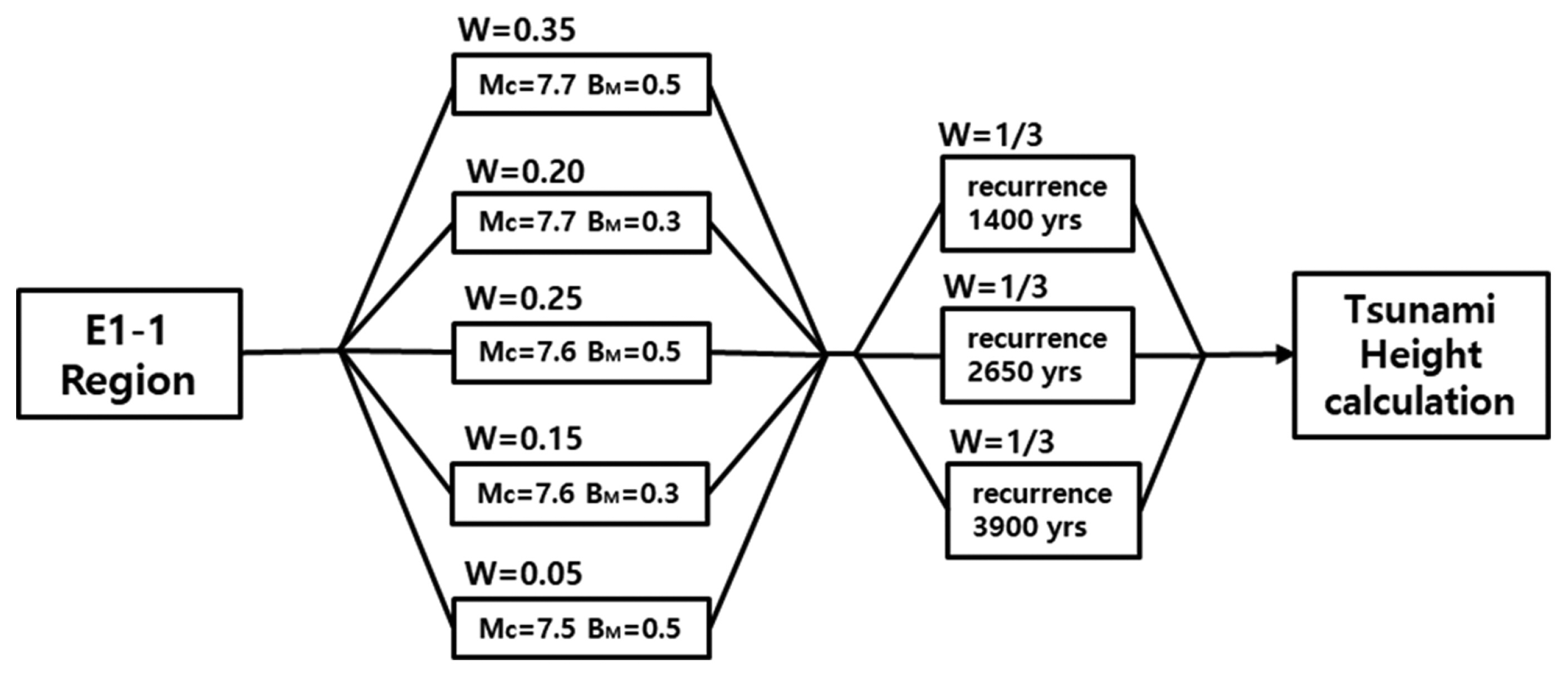
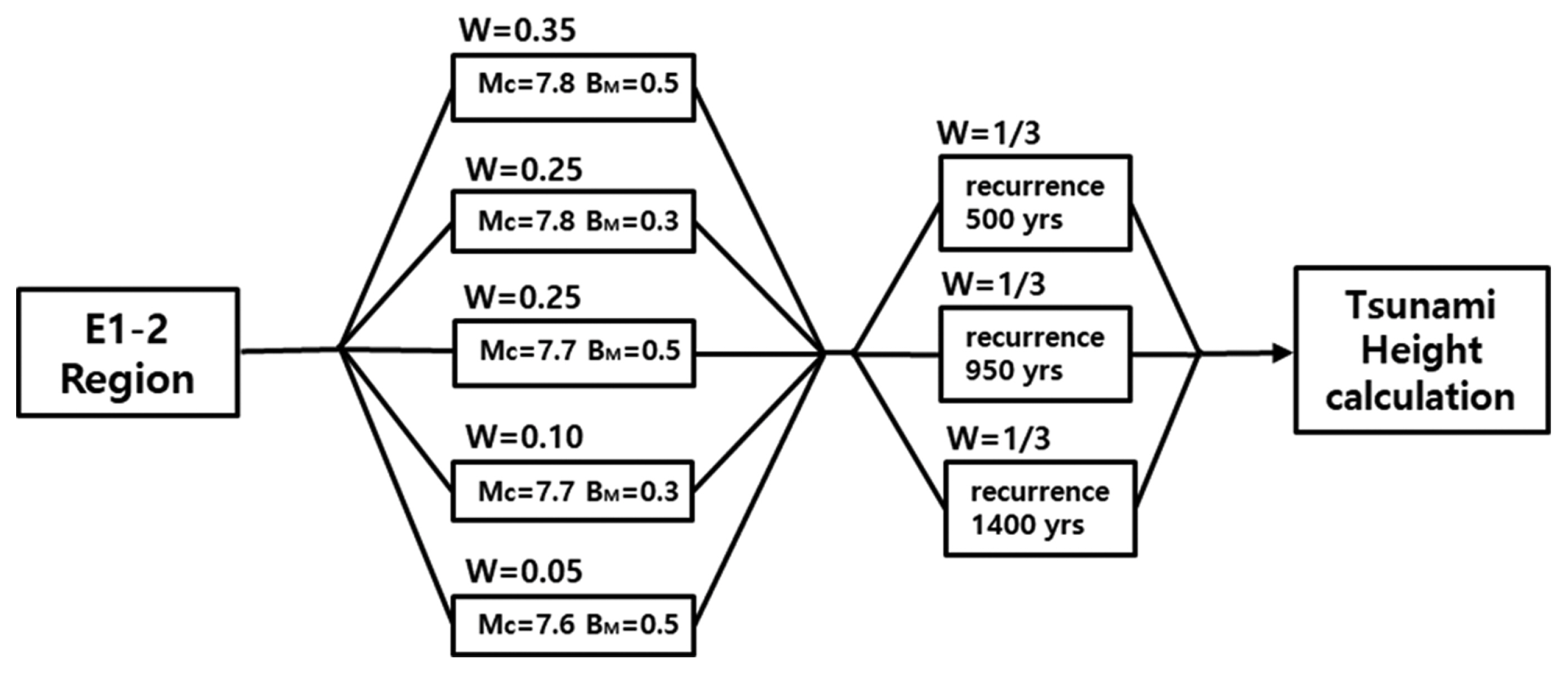
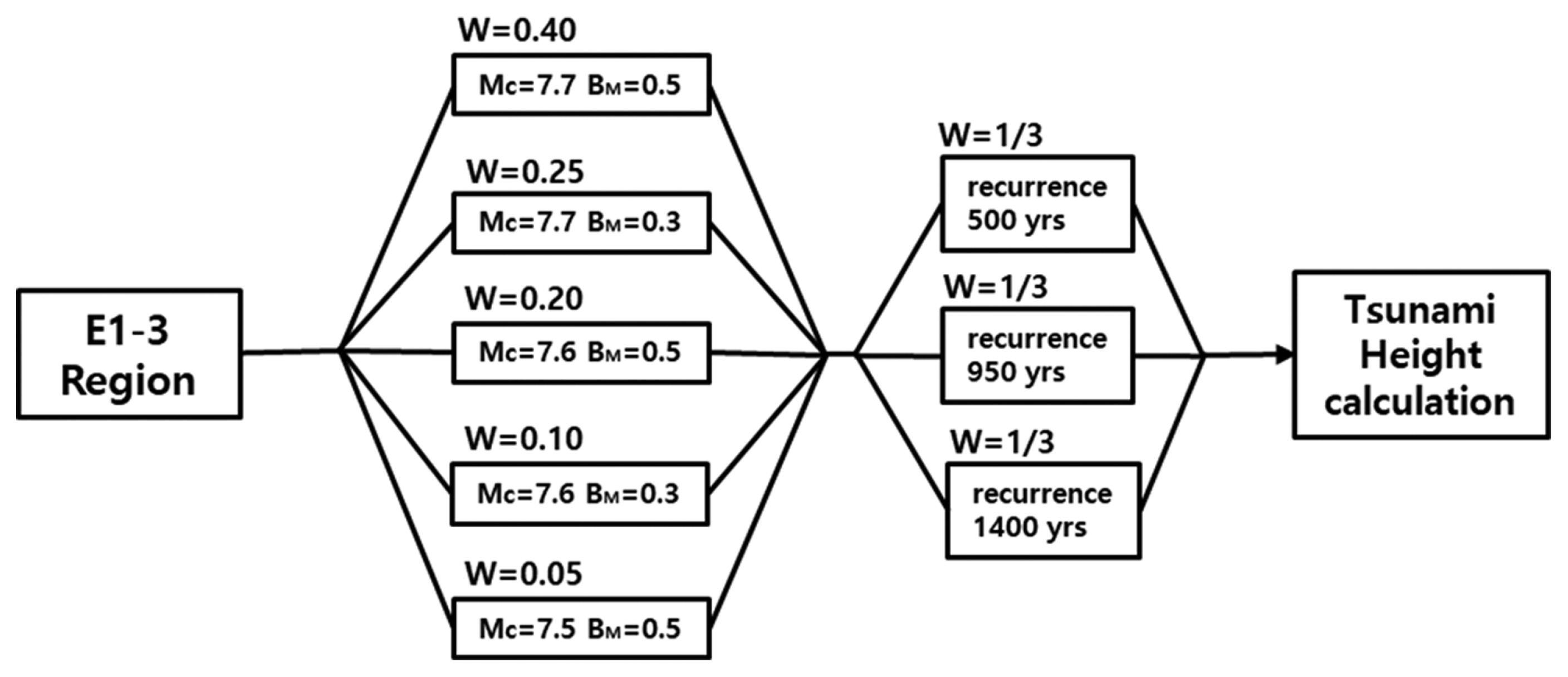
Figs. 5~7은 각각 E1-1, E1-2 및 E1-3 세그먼트에 대한 로직트리이다. E0 세그먼트를 제외한 나머지 세그먼트들의 재현기간에 대해서는 각 세그먼트에 대해 양극단 사이의 범위로 주어진다. 예를 들어 E1-1 세그먼트에 대해 Fig. 5에 보인 바와 같이 1,400년에서 3,900년 사이의 양극 값이 제시되어 있고, 이 양극단 사이에서 특정 재현기간의 중요성은 균일하다고 되어 있다(JSCE, 2016). 따라서 양극단 사이의 중앙치는 2,650년이므로 로직트리 분기를 양극단과 중앙치의 3가지로 정하였으며, 각 로직트리 분기의 가중치 w를 1/3로 부여하였다.
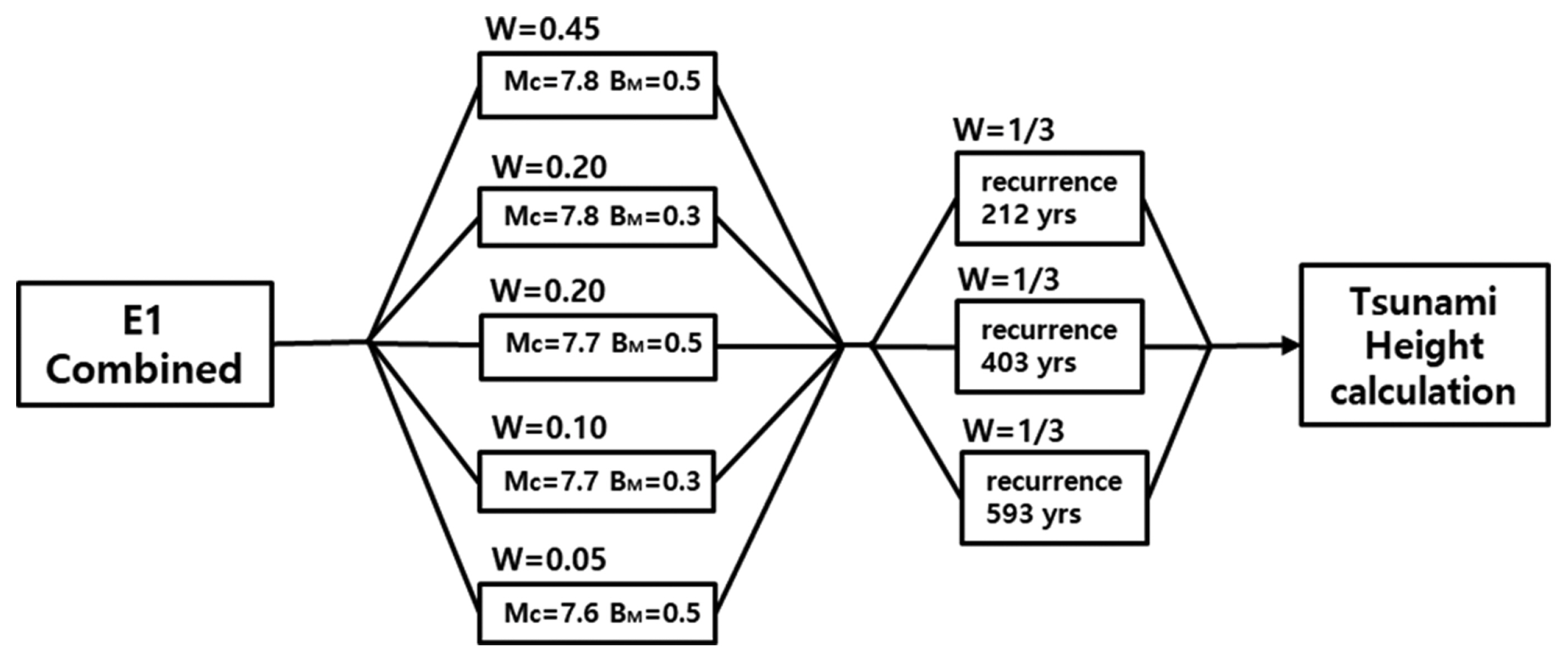
Fig. 8은 E1-1, E1-2 및 E1-3 세그먼트가 서로 구분되어 있지 않고 1개의 세그먼트로서 일체로 거동할 가능성에 대한 로직트리이다. E1-1, E1-2 및 E1-3 세그먼트와 같이 각 세그먼트가 독립적으로 거동하는 경우에는 단층활동이 주어진 1개의 세그먼트 내에서만 발생하므로 인접하는 2개의 세그먼트에 걸쳐 발생하는 지진은 없다고 가정한다. 반면에 일체로 거동하는 경우에는 E1에 속한 전체 세그먼트의 어디에서도 지진이 발생할 수 있다고 가정한다. E1 일체 영역에서의 지진규모 분기는 Table 1의 E1-1, E1-2, E1-3에서 발생한 지진 중 가장 큰 규모를 근거로 설정하였다. 주어진 진원위치에서 의 지진 발생빈도는 재현기간의 역수로 주어지며 과거 지진 발생 실적으로부터 추론하여 구한다. E1-1 세그먼트에서의 재현기간은 평균적으로 2,650년에 1회 발생하며, 재현기간의 불확실성을 고려하기 위해 1,250년의 편차를 주어 하한치를 1,400년, 상한치를 3900년으로 정하였다(JSCE, 2015). E1-2와 E1-3의 경우에도 이러한 개념으로 하한치를 500년, 상한치를 1,400년으로 정하였다. E1-1, E1-2, E1-3의 3개 세그먼트를 일체로 고려하는 경우에는 각각의 발생빈도를 더하여 역수를 취하여 결정한다. 즉, 3개 세그먼트 각각의 발생빈도 하한치를 더하면 1/1,400 + 1/500 + 1/500 ≒ 1/212이므로 역수를 취하면 재현기간의 하한치는 212년이며, 발생빈도 상한치 합은 1/3,900 + 1/1,400 + 1/1,400 ≒ 1/593이므로 역수를 취하면 재현기간의 상한치는 593년이다. 중앙치는 같은 방법으로 재현기간이 403년이 된다.
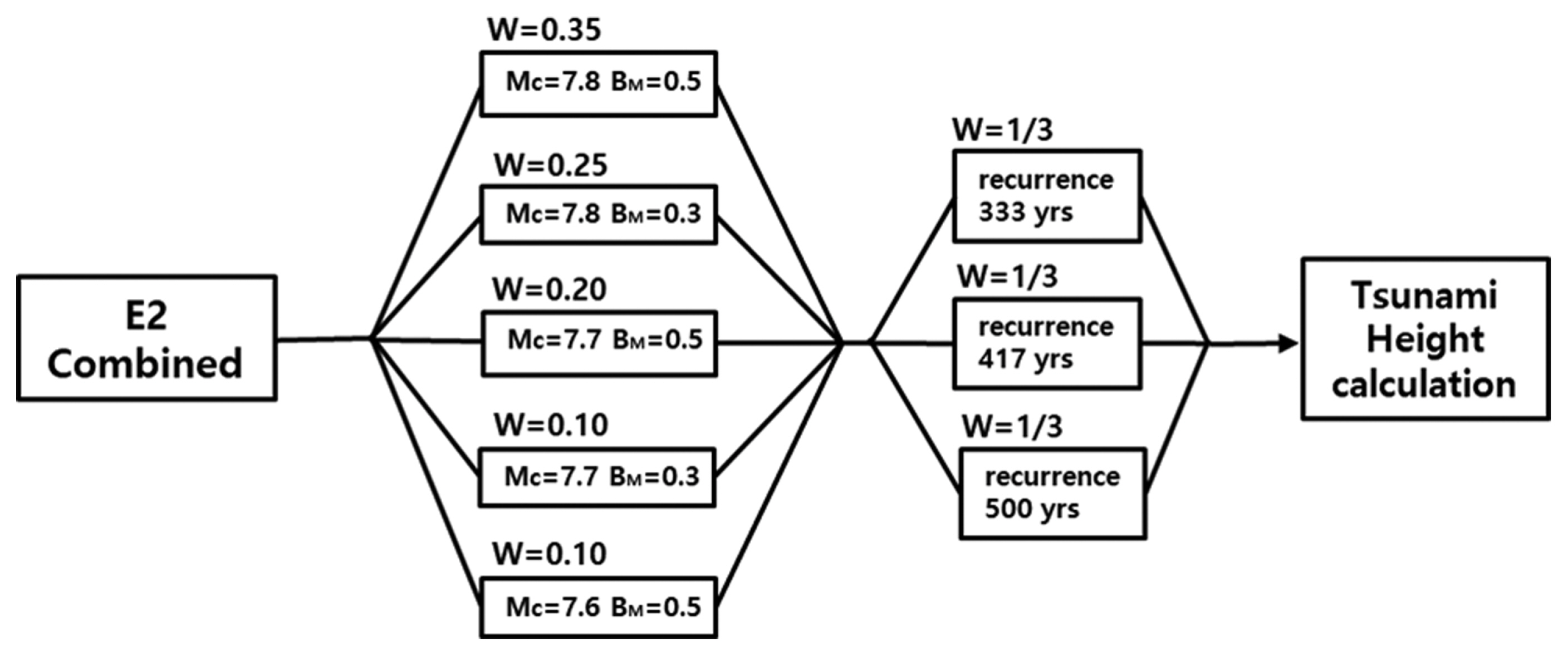
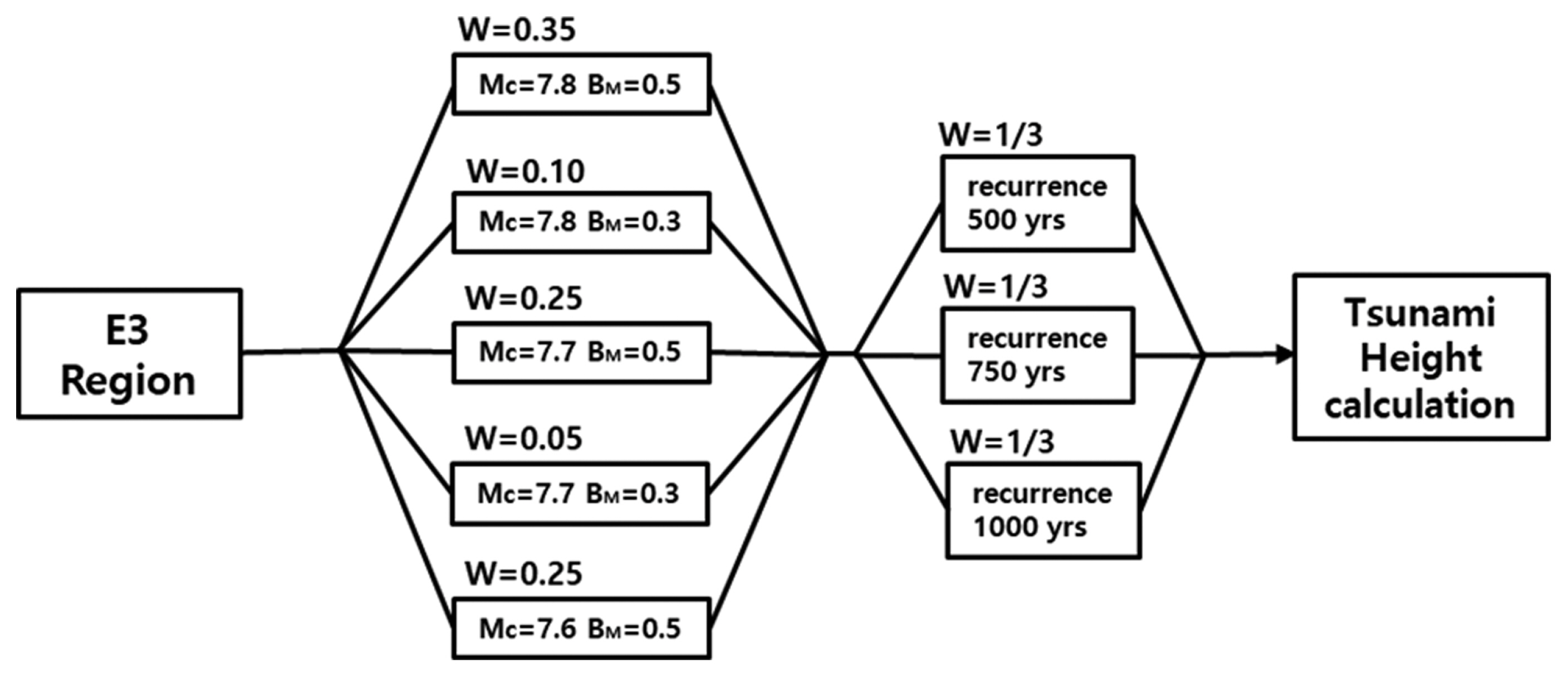
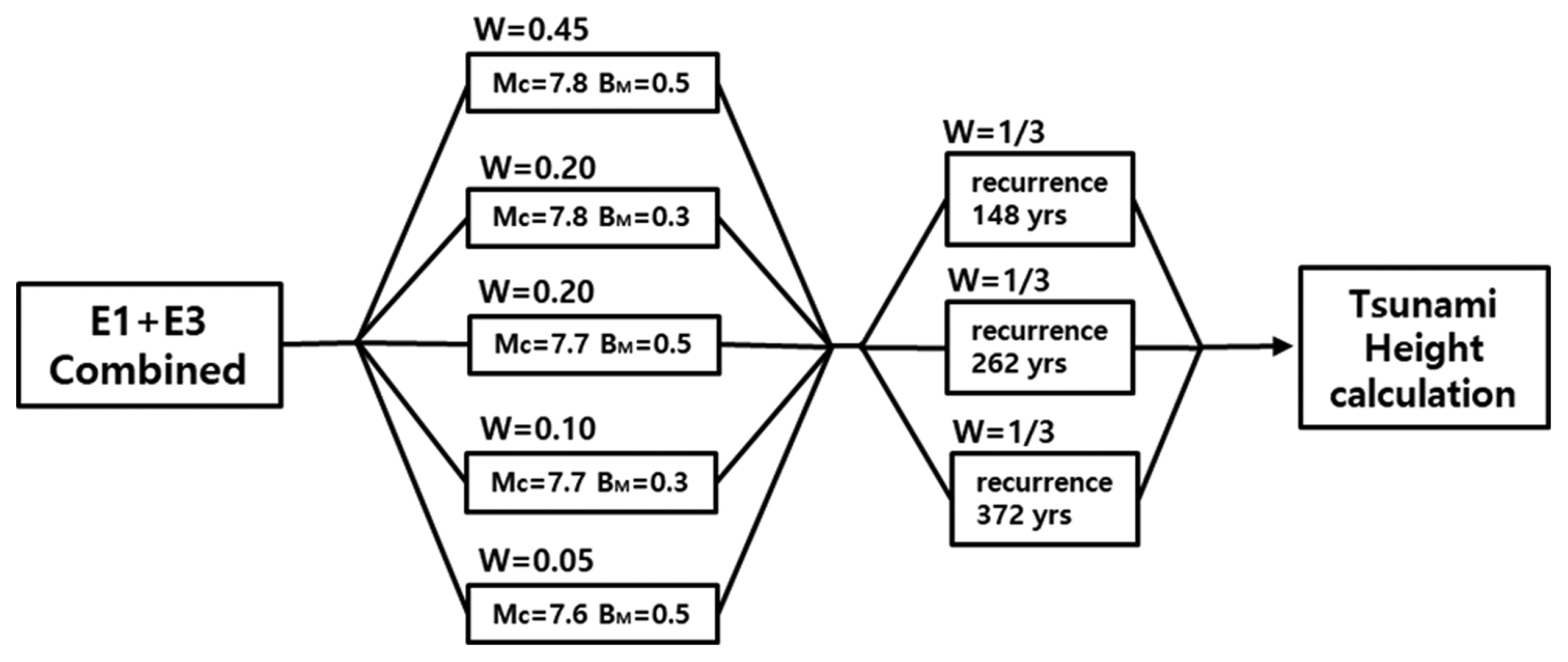
Fig. 9는 동해 동연부 E2 세그먼트에 대한 로직트리이다. 원래 JSCE(2016)에서는 E2 세그먼트를 E2-1, E2-2, E2-3의 3개 세그먼트로 구별하였으나, 이렇게 구분하면 각각의 세그먼트 길이가 다른 세그먼트들보다 훨씬 짧아 큰 규모의 지진 발생이 불가능하다. 3개의 E2 세그먼트가 일체로 작용할 경우에만 Mw 7.7 이상의 큰 지진 발생이 가능하므로 본 연구에서는 E2 세그먼트가 일체로 거동하는 경우만을 고려하였다. Fig. 10은 동해 동연부 E3 세그먼트에 대한 로직트리이다. Fig. 11은 E1과 E3 세그먼트가 일체로 거동하는 경우에 대한 로직트리로 규모와 재현기간은 E1 세그먼트의 일체화가 선행되어야 하며 E3는 E1 일체 조건의 하위개념에 속하므로. E1+E3 일체 조건에서는 E1 세그먼트의 일체 조건에 사용된 분기구성 방식을 적용하였다. 지진 최대규모와 재현 기간은 Table 1에 제시된 바에 근거한다.
2.2.2 류큐 트렌치
류큐 트렌치에 대한 지진 규모는 동해 동연부에 적용하는 방식과는 다르다. 동쪽의 북아메리카 판과 서쪽의 유라시아판이 충돌하는 동해 동연부의 단층대는 충돌하는 2개의 판이 압축을 받으며 역단층 거동을 한다. 이와는 달리 류큐 트렌치에서는 필리핀해 판이 유라시아 판 밑으로 섭입하면서 2개 판 사이의 마찰력에 의한 응력이 쌓여 한계치에 도달하면 지진이 발생하여 응력을 해소한다. 이러한 섭입대에서의 지진 규모와 재현기간은 응력강하량 모델을 사용한다. 먼저 단층의 면적 S(m2)와 지진발생으로 인한 평균응력강하량 ∆σ(MPa)가 주어지면 이로부터 식(1)을 이용하여 지진모멘트 M0(N·m)가 결정되며(Eshelby, 1957), 식(2)를 이용하면 M0로부터 지진규모 Mw를 구할 수 있다.
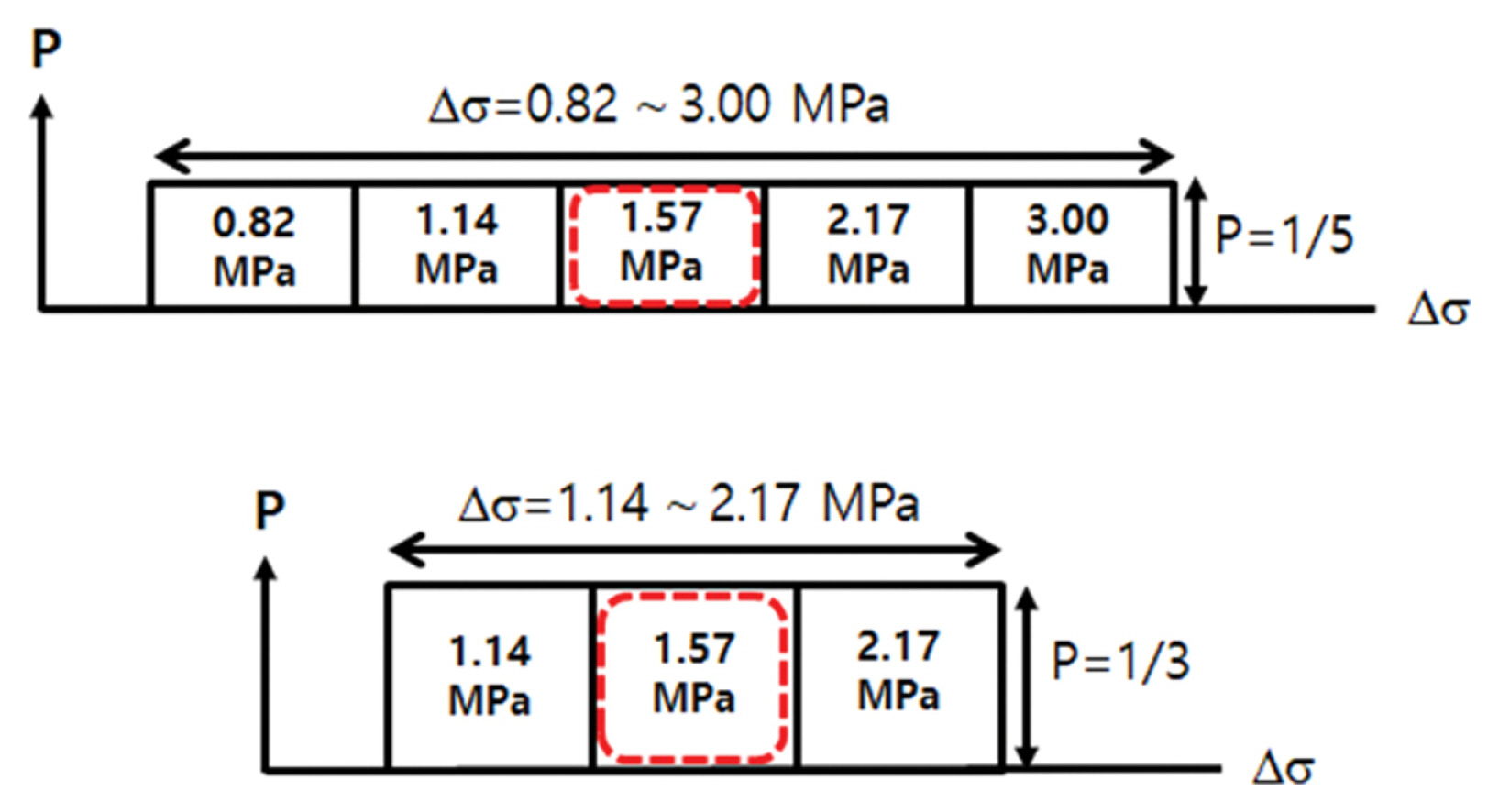
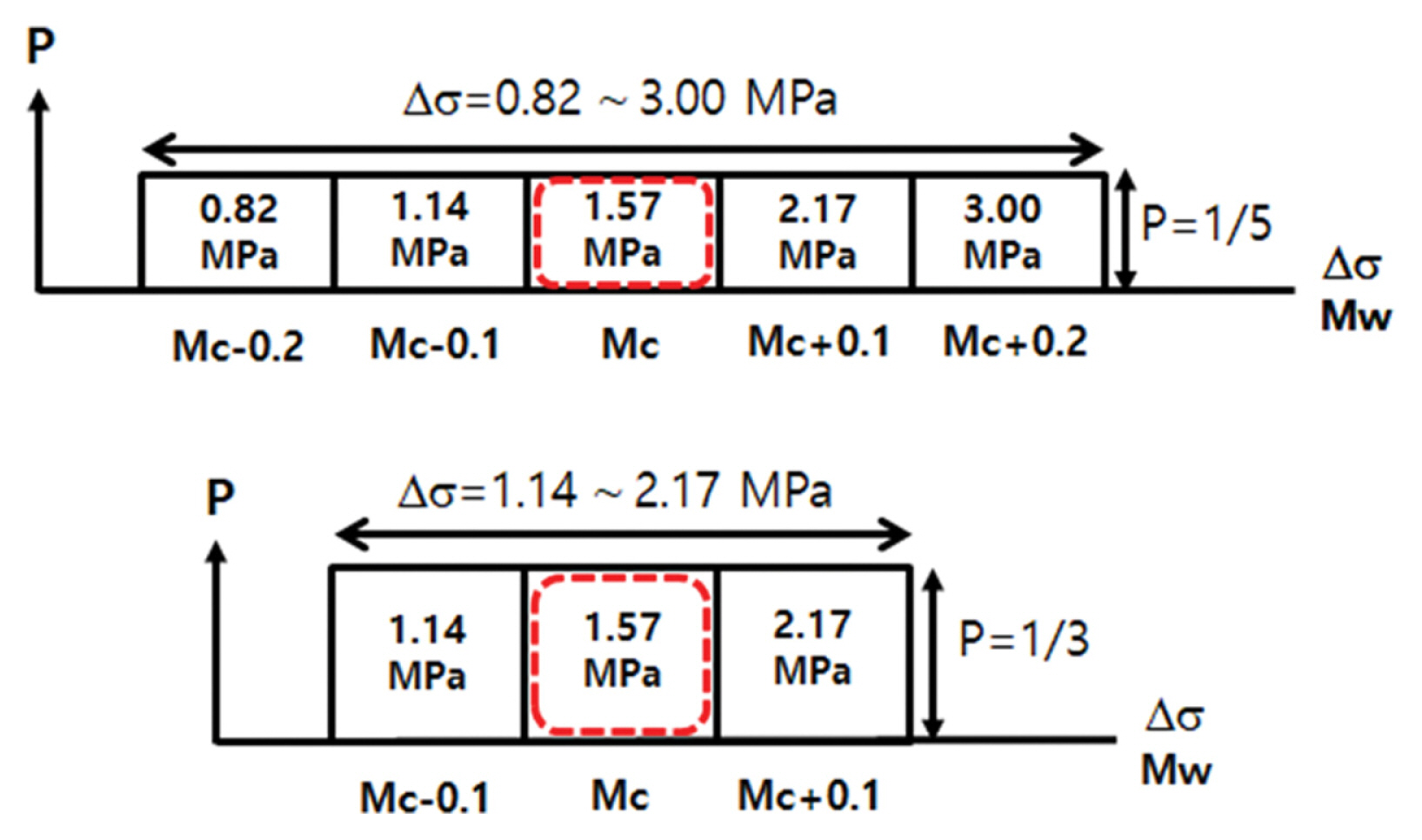
응력강하량 모델은 지진이 발생하면서 축적되었던 단층면 사이의 응력이 ∆σ만큼 해소된다는 개념이다. 섭입대에서 응력강하량의 평균치는 1.57 MPa로 알려져 있으며(Murotani et al., 2013), 이에 대한 불확실성을 고려하기 위해 응력강하량의 범위를 준다. 가장 보편적으로 검토되는 범위는 Fig. 12에 보인 바와 같이 평균치인 1.57 MPa을 중심으로 0.82 MPa < ∆σ < 3.00 MPa과 1.14 MPa < ∆σ < 2.17 MPa의 2가지 범위이다. 첫 번째 범위는 Fig. 12에 보인 바와 같이 0.82 MPa < ∆σ < 3.00 MPa를 5개 구간으로 나누어 각 구간에 대한 응력강하량을 차등 부여한다. 양 끝 값은 Murotani et al.(2013)이 제안한 응력강하량의 ±1 표준편차에 해당하는 구간이다. 두 번째 범위는 ±0.5 표준편차에 해당하며 3개 구간으로 나누는 방식이다(JSCE, 2016). 각 구간별 응력강하량에 대한 지진규모를 식(1)에 의해 구해보면 구간 별 Mw 차이가 대략 0.1이 되도록 정해져 있다. 따라서 Fig. 13에 보인 바와 같이 0.82 MPa < ∆σ < 3.00 MPa의 응력 강하량 범위는 지진규모의 범위인 Mc ± 0.2, 즉 BM = 0.5에 해당한다. 같은 방법으로 1.14 MPa < ∆σ < 2.17 MPa 범위는 Mc ± 0.1, 즉 BM = 0.3에 해당한다.
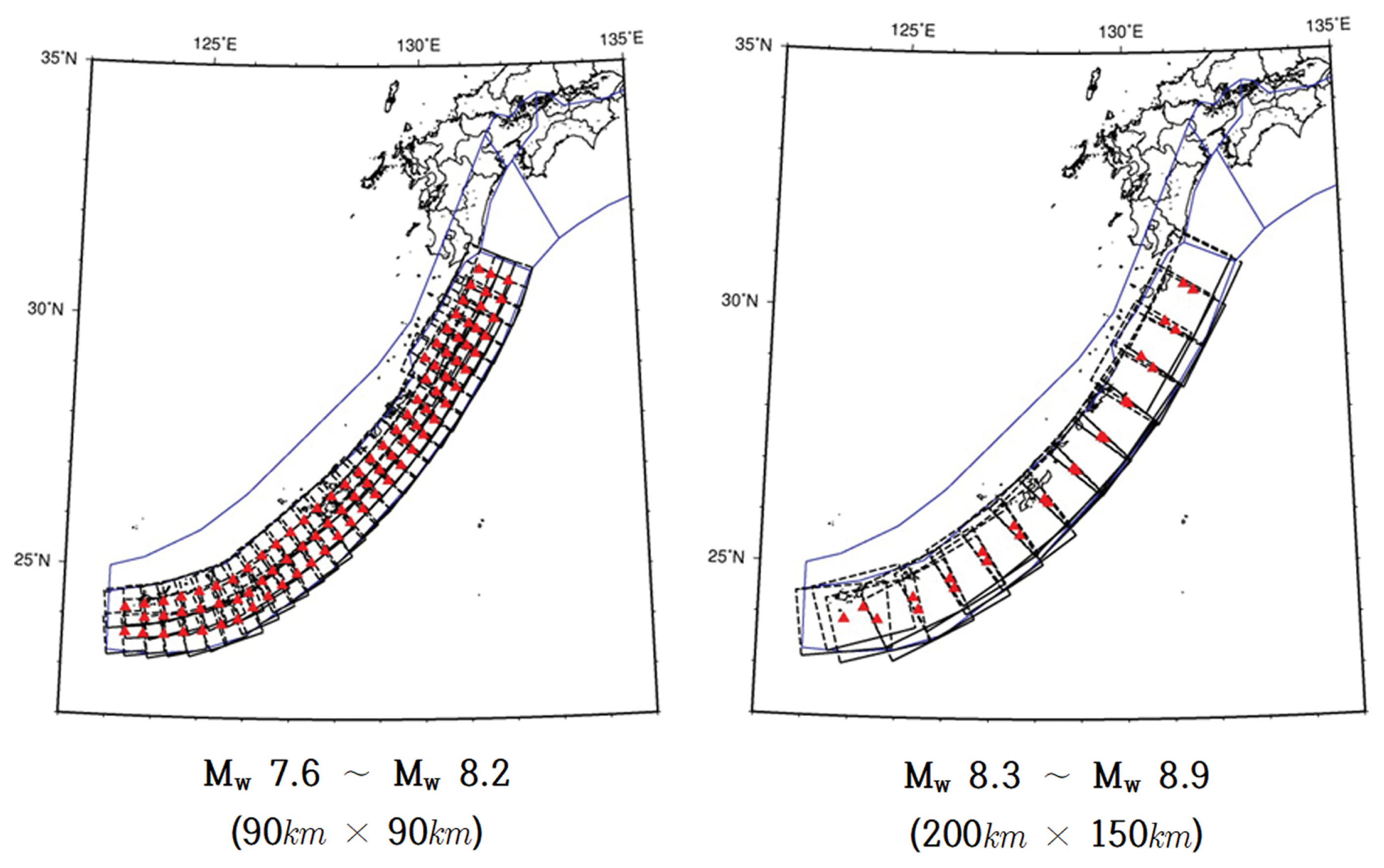
일본 주변의 다른 지진대에 비해 류큐 트렌치는 지진발생 과거 기록이 드물고, 지진단층 특성에 대한 연구도 상대적으로 빈약하여 이곳에서의 지진 규모에 대한 불확실성이 상대적으로 높다. 따라서 류큐 트렌치에 대한 지진의 최대 규모는 기왕 최대치(역사지진)인 Mw 8.0에 대해 검토하는 것 이외에도 지진규모에 대한 불확실성을 고려하고 또한 보수적인 평가를 위해 기왕 최대치인 Mw 8.0의 4배 규모인 Mw 8.4 정도의 대규모 지진을 추가로 상정하는 것이 합리적이다. 일본 지진조사연구추진본부 지진조사위원회(Headquarters for Earthquake Research Promotion of Japan: HERP, 2013)에서는 Mw 8.3~Mw 8.9의 지진에 대해서 단층면적 30,000 km2를 상정하였다. 그러나 본 연구에서 적용한 응력강하량 모델에 따르면 해당 단층면적 30,000 km2에서 발생하는 지진의 규모는 불확실성을 고려하면 Mw 8.1~Mw 8.5로 평가된다. 따라서 대규모 상정지진의 중심규모는 Mw 8.3으로 설정된다. HERP(2013)는 Mw 7.6~Mw 8.2의 지진에 대해서는 8,100 km2의 단층면적으로 제시하였으며, Fig. 13에 보인 응력강하량의 중앙치인 1.57 MPa를 적용할 경우 중심규모가 Mw 7.7로 산정됨에 따라 Mw 7.5부터 Mw 7.9까지의 지진규모를 고려하게 된다. 이 경우 기왕최대규모인 Mw 8.0에 해당하는 규모를 고려할 수 없으므로 중심규모를 0.1만큼 증가시켜 Mw 7.8이 되도록 하여 불확실성을 고려한 규모가 Mw 7.6~Mw 8.0이 되도록 면적을 9,900 km2로 조정하였다. Mw 7.8과 Mw 8.3을 규모 중앙치로 선정하면, Mw 7.6~Mw 8.5의 규모를 0.1 간격으로 검토하게 되며, 기왕최대규모와 이를 초과하는 대규모 지진 규모 모든 경우를 다룰 수 있다. 여기에 Mw 7.6~Mw 8.2 범위의 규모로 설정된 선단부 지진의 연동 가능성의 유무를 적용하여 연동을 고려하지 않으면 Mw 7.6~Mw 8.5, 연동을 고려하면 Mw 7.8~Mw 8.6의 지진규모를 고려하게 된다. 따라서 최소 Mw 7.6부터 최대 Mw 8.6의 광범위한 경우를 검토하게 된다.
응력강하량 모델에서 지진의 발생 재현기간 Y는 다음 식으로 구하며, 재현기간에 대한 로직트리는 별도로 존재하지 않는다.
여기서 Y는 재현기간(년), c는 고착도(coupling)로서 0 < c < 1의 범위이며, S(km2)는 단층면적이다. 따라서 류큐 트렌치에서의 지진 재현기간은 동해 동연부 지진대와는 달리 단층면 , 응력강하량과 고착도에 따라 달라진다. 이상과 같은 분석에 근거하여 류큐 트렌치의 각 지진원에 대한 지진규모 및 재현기간에 대한 로직트리 분기를 설정하였다. 우선 Mw 8.3 정도의 대규모 상정 지진 발생 여부에 따른 분기와 응력강하량 범위에 따른 분기, 고착도에 따른 분기, 그리고 섭입대 선단부에서 발생하는 선단부 지진(tsunami earthquake)과의 연동 빈도 분기와 선단부 지진 규모 분기의 복잡한 로직트리 분기가 고려된다. 류큐 트렌치에 대한 고착도는 기존 연구자료(Scholz and Campos, 2012)에 의하면 일본 해구나 난카이 트러프에 비해 상대적으로 작은 것으로 알려져 있어 c = 0.1분기에 90%의 높은 가중치가 부여되었다. 이는 류큐 트렌치에서의 지진 발생 빈도가 다른 섭입대에 비해 매우 낮은 현 상과도 부합된다. 섭입대 선단부 지진은 섭입대 상판(upper plate)의 선단에서 매우 좁고 긴 단층 파괴 현상을 고려하기 위한 것으로 류큐 트렌치에서 선단부 지진에 대한 조사나 연구 실적이 없다. 따라서 섭입대 선단부 지진에 대해서는 JSCE(2016)에 제시되어 있는, 일본 해구에 적용되는 방법을 차용하여 연동빈도 분기와 지진규모 분기를 구성하였다. Fig. 14는 류큐 트렌치의 북부 세그먼트에 대한 로직트리이며, 이는 중부 세그먼트에도 적용된다.
2.3 단층의 거동 특성
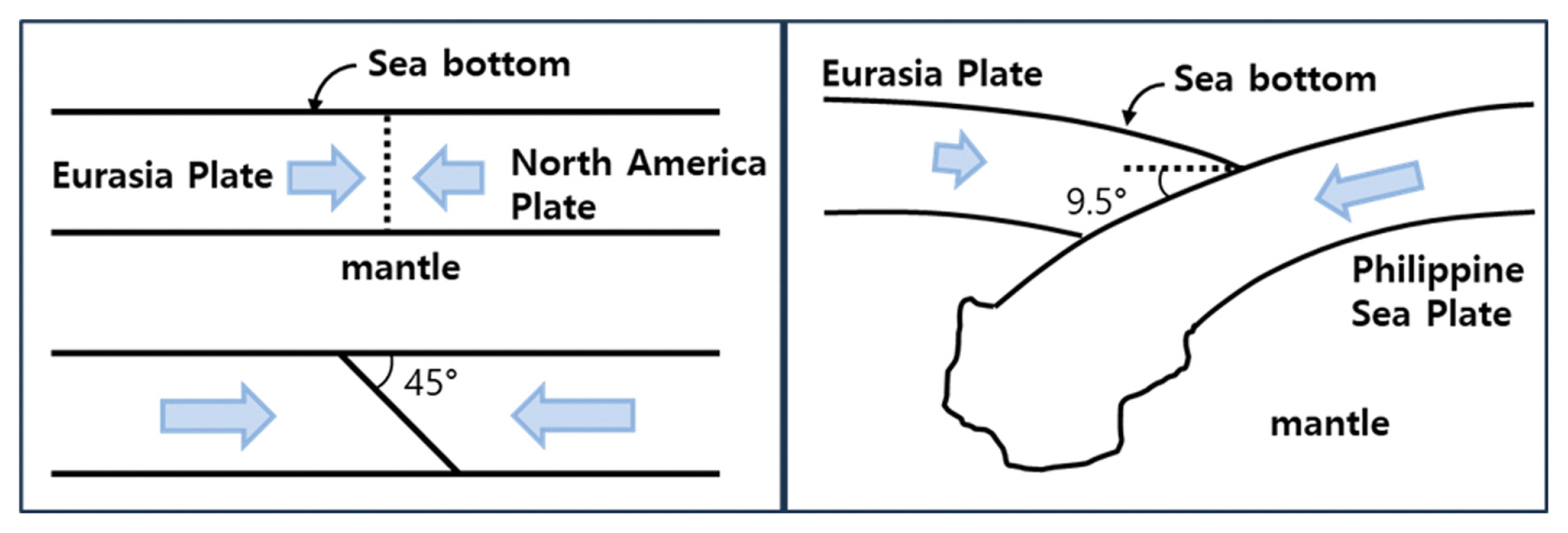
지진해일을 발생시키는 해저 지진의 위치, 지진규모 및 재현기간 등이 정해지면 해일고 추정모델의 기본 입력자료인 지진해일의 초기 파형을 결정하는 단층의 거동 특성을 파악해야 한다. 동해 동연부에서 발생하는 지진의 거동은 류큐 트렌치와 같은 섭입대에서 발생하는 지진과 매우 다르다. Fig. 15에 보인 바와 같이 동해 동연부 지진은 태평양 판이 북아메리카 판을 밀어 상대적으로 정지되어 있는 유라시아판과 동해 동연부 단층대에서 만나 강한 압축력을 받아 발생한다. 두개의 판은 수평을 유지하며 충돌하므로 어느 판이 다른 판 아래로 섭입하는 현상은 발생하지 않는다. 강한 압축력을 받는 균일 두께의 고체 부재에서 압축력과 45o의 경사진 사면을 따라 전단파괴가 쉽게 발생함은 고체역학에서 잘 알려진 현상이다. 지각판 지질 특성에 따라 단층 파괴면의 경사각은 약간씩 변하며 45o를 중심으로 30o에서 60o 사이의 범위에 존재한다. 반면 류큐 트렌치의 단층면 경사각은 필리핀해판이 유라시아판 밑으로 섭입하면서 발생하여 9.5o의 일정한 경사각을 이룬다. 경사각 이외에도 동해 동연부 지진과 류큐 트렌치 지진의 특성은 매우 다르다.
2.3.1 동해 동연부
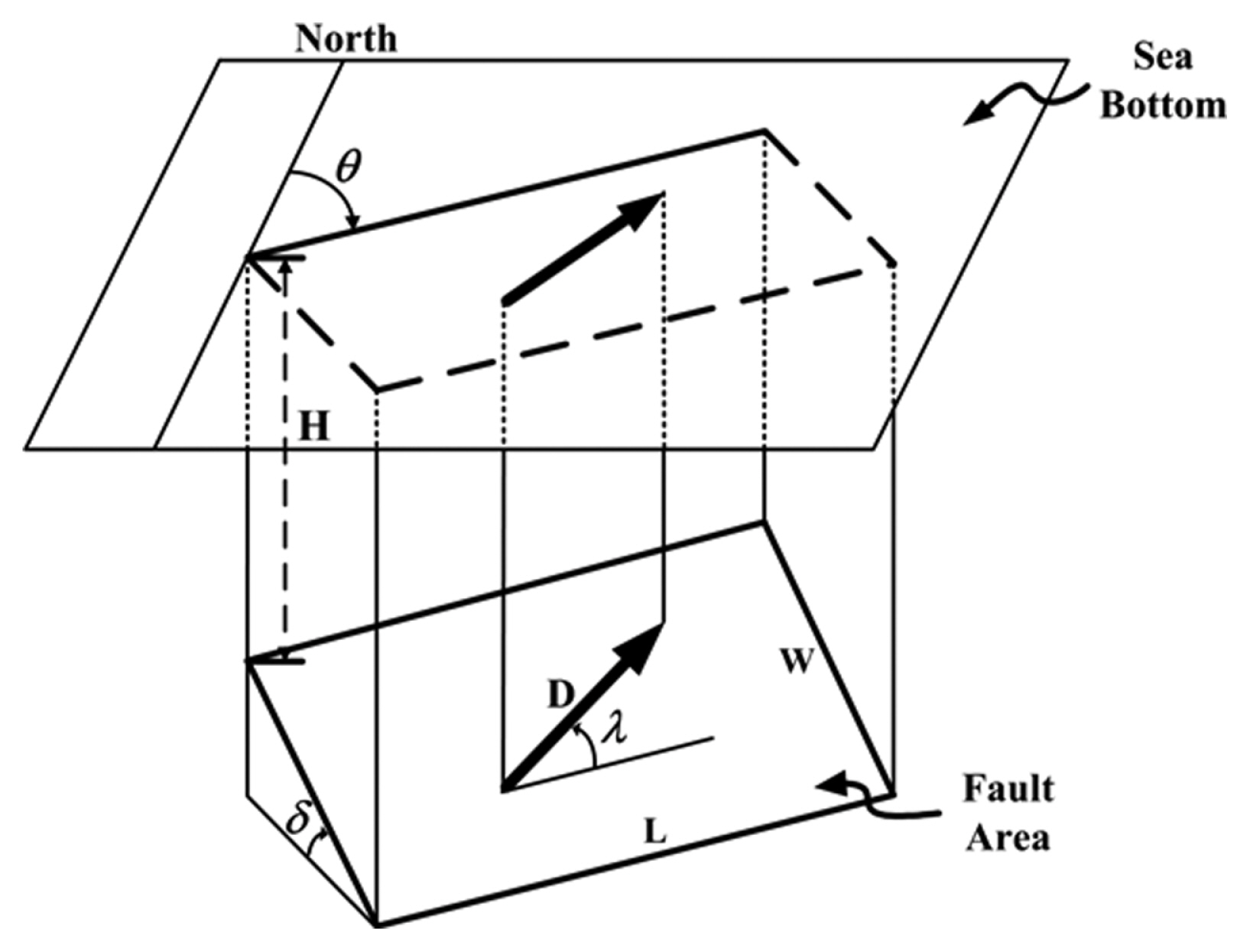
지진해일의 초기 파형을 결정하는 단층의 거동 특성, 즉 단층 파라미터에는 Fig. 16에 보인 바와 같이 단층 길이 L, 단층 폭 W, 주향각 θ, 경사각 δ, 활동각 λ, 단층변위량, 즉 활동량 D, 단층면 상연의 깊이 H, 단층변위 분포(asperity) 등이 있다. 이들 중 상연의 깊이 H는 일반적으로 1 km를, 활동각 λ는 90o를 사용하면 동해 동연부의 지진에 대해 보수적인 결과를 얻을 수 있다.
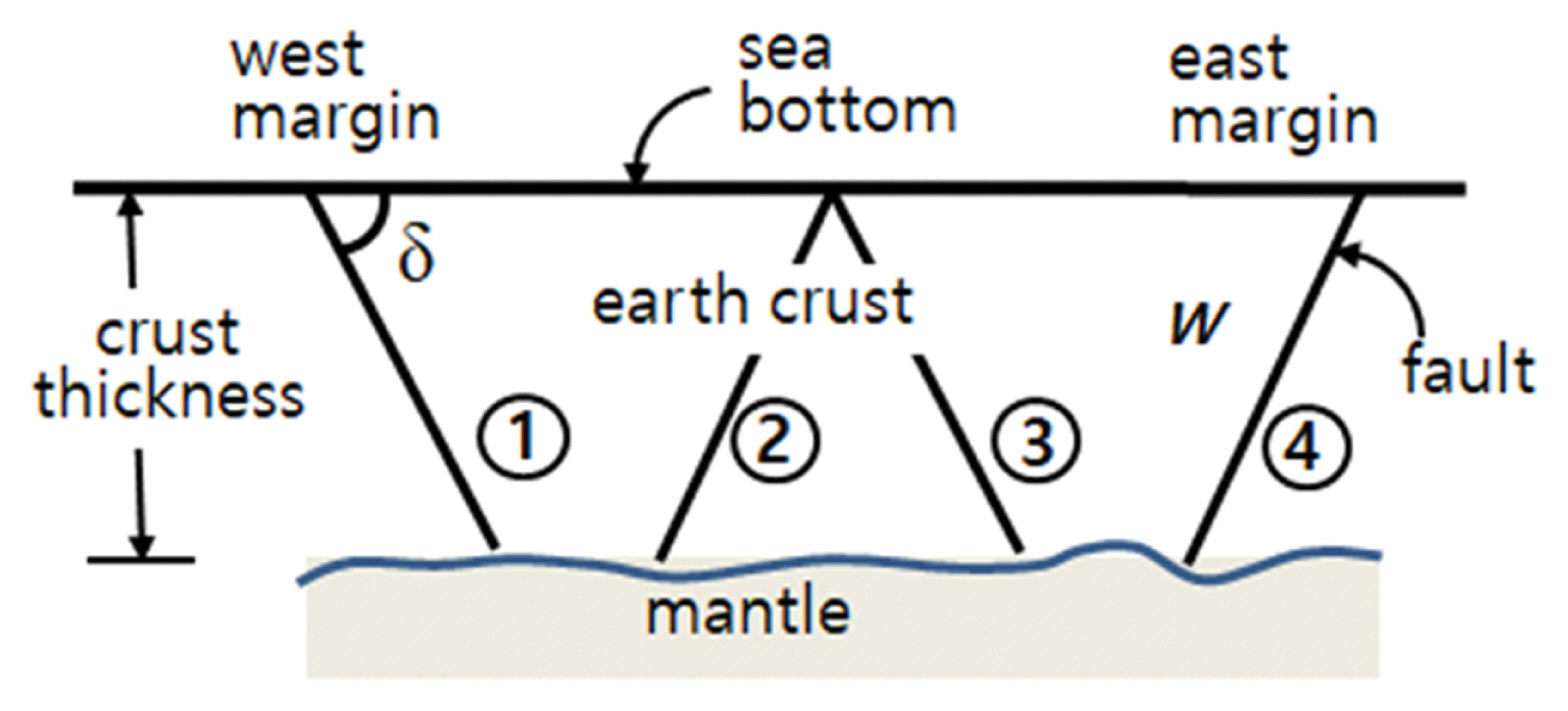
단층의 폭(W)은 지진이 발생하는 지각의 두께에 따라 최대 한계치가 존재하며 식(4)는 최대 단층의 폭을 계산하기 위한 관계식을 보여준다. 예를 들면 JSCE(2016)에서는 동해 동연부, 즉 일본 서안 지역의 경우 지진이 발생하는 지각의 두께가 최대 20 km라고 제시한 바 있다. 따라서 동해 동연부 지각의 두께 20 km와 단층면 경사각 δ(dip angle)와의 관계를 통해 물리적으로 최대 발생할 수 있는 단층의 폭 W(km)가 결정된다.
일본 국토교통성(Ministry of Land, Infrastructure, Transport and Tourism, 2014)의 연구결과에 따르면 동해 동연부에서의 경사각 δ(dip angle)은 대부분 45o의 값을 가지며 통상 30o ~ 60o의 값을 가진다. 따라서 불확실성을 고려하기 위해 15o 간격으로 나누어 총 3개 분기로 구성하였다. JSCE(2016)에서 경사각 자체 및 발생위치에 대한 불확실성을 고려하여 권장하는 로직트리 분기는 다음 Fig. 17과 Fig. 18에 보인 바와 같이 δ를 단층대의 폭방향으로, 즉 동서방향으로 이동시켜 각각 4가지 분기(slip location ①~④)를 고려한다.
지진규모 Mw와 단층 폭 W(m)가 주어지면 스케일링 법칙(scaling law)에 의해 단층면적 S(m2)와 단층 길이 L(m) 및 평균 단층변위량 D(m)를 결정한다. 스케일링 법칙에는 일본의 ‘확률론적 지진해일 해저드 해석 방법’(JSCE, 2011)과 ‘원자력발전소의 지진해일 평가기술 2016’(JSCE, 2016)에서 제안하는 2가지가 있다. JSCE(2011)에서 제안하는 방법은 단층변위량에 제한을 두지 않는 반면, JSCE(2016)에서는 단층 변위량에 최대치(Dmax = 4.5 m)가 존재한다는 개념으로 이 최대치를 포화 변위량이라 한다. 첫 번째 2011년의 스케일링 법칙(scaling law 1)은 주어진 지진규모 Mw와 단층폭 W(m)에 대응하는 지진모멘트 M0(N·m)와 단층길이 L(m), 단층 변위량 D(m)를 다음과 같이 결정한다.
여기서 μ는 지각의 강성률로서 μ = 3.5 × 1010 N/m2이다.
한편 두 번째 2016년의 스케일링 법칙(scaling law 2)은 주어진 지진규모 Mw와 단층폭 W(m)에 대응하는 지진모멘트 M0(N·m)를 다음과 같이 결정한다.
이 지진모멘트 M0(N·m)로부터 단층면적 S(m2)을 다음 식에 의해 구한다.
단층길이 L(m)은 단층면적 S(m2)와 단층폭 W(m)를 이용하여 다음과 같이 구한다.
또한 평균 활동량, 즉 단층변위량 D(m)는 다음과 같이 구한다.
두 번째 스케일링 법칙은 지진규모 Mw 7.7 이상의 지진에 대해 단층변위량이 포화치인 D = 4.5 m로 일정해진다. 따라서 큰 지진규모에 대해서는 단층길이가 지나치게 길어져 세그먼트 길이를 초과하는 경우가 발생한다. 본 연구에서는 이러한 불합리한 점을 고려하여 2011년의 스케일링 법칙을 추가로 고려하는 로직트리 분기를 설정하였다.
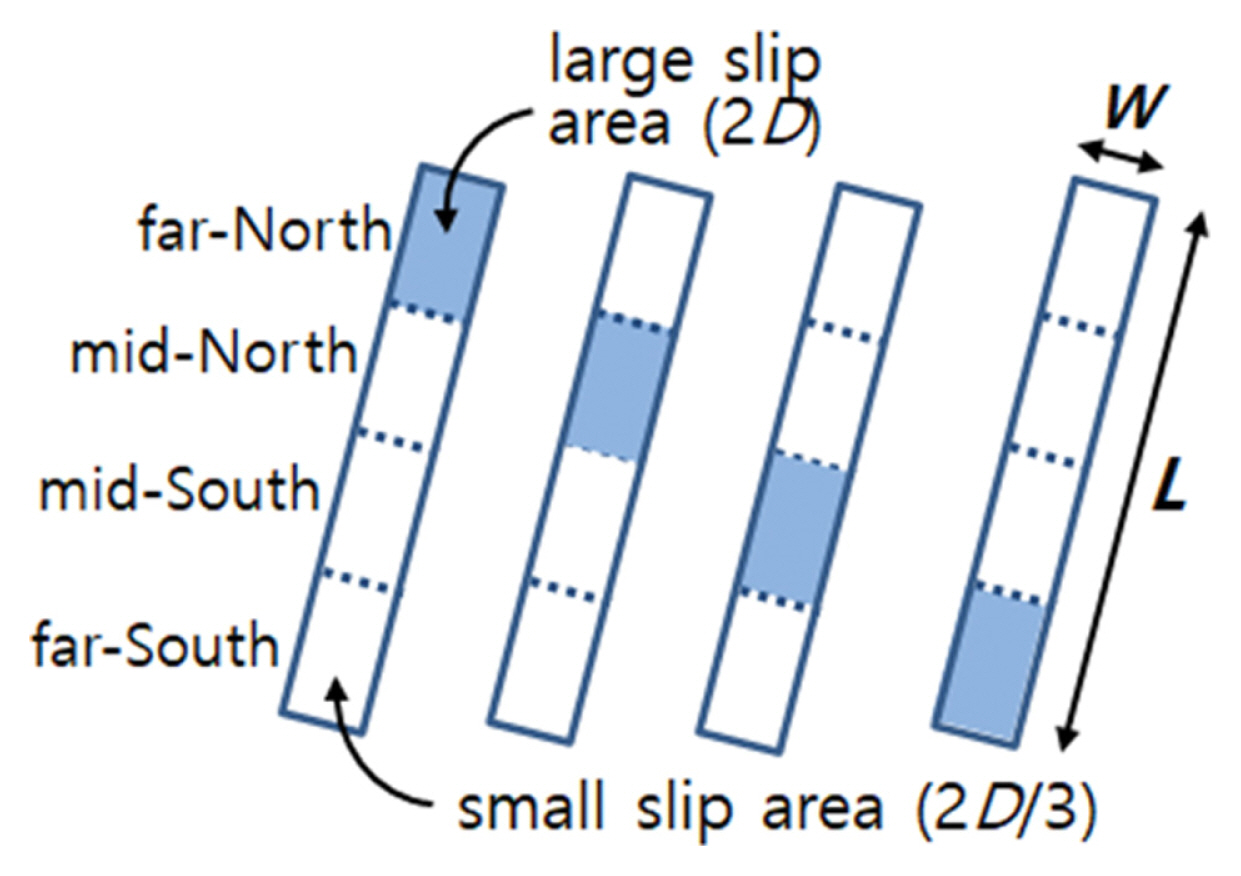
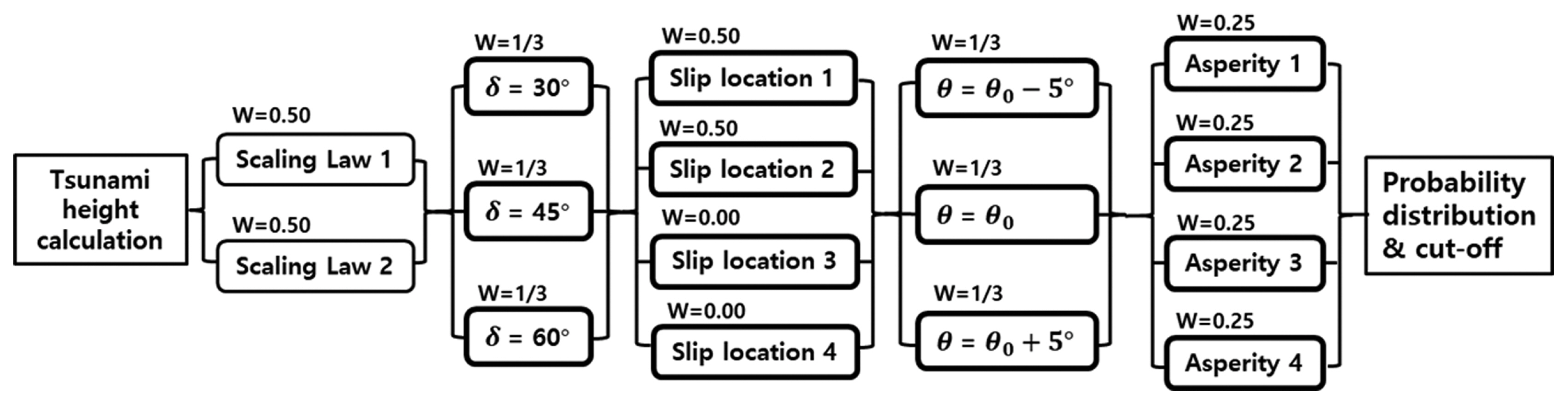
지진규모가 큰 장단층의 활동량에 대한 불균일성(asperity)을 고려하기 위해서는 전체 단층 길이를 4등분하여 그 중 1/4면적에 대해 평균활동량 D의 2배를, 나머지 3/4 면적에 대해 D의 2/3배를 적용하고, 큰 활동량 영역은 Fig. 19에 보인 바와 같이 4가지 경우로 고려한다.
지진규모가 작은 지진은 단층길이도 짧아 주어진 세그먼트 내에서 남북으로 걸쳐 여러 곳에서 발생할 수 있다. 이 경우 1개 세그먼트에서 k개의 위치 변동을 고려한다고 가정하면 각각의 위치에 대한 지진해일고를 구하고 대수정규분포와 타절을 고려한 다음, 각각의 확률분포 곡선의 발생확률을 1/k로 한 다음 이들을 합산하여 하나의 확률분포 곡선을 구한다. 이는 지진규모의 불확실성을 고려하기 위해 Mc와 BM으로 주어진 분기의 처리 방법과 동일하다.
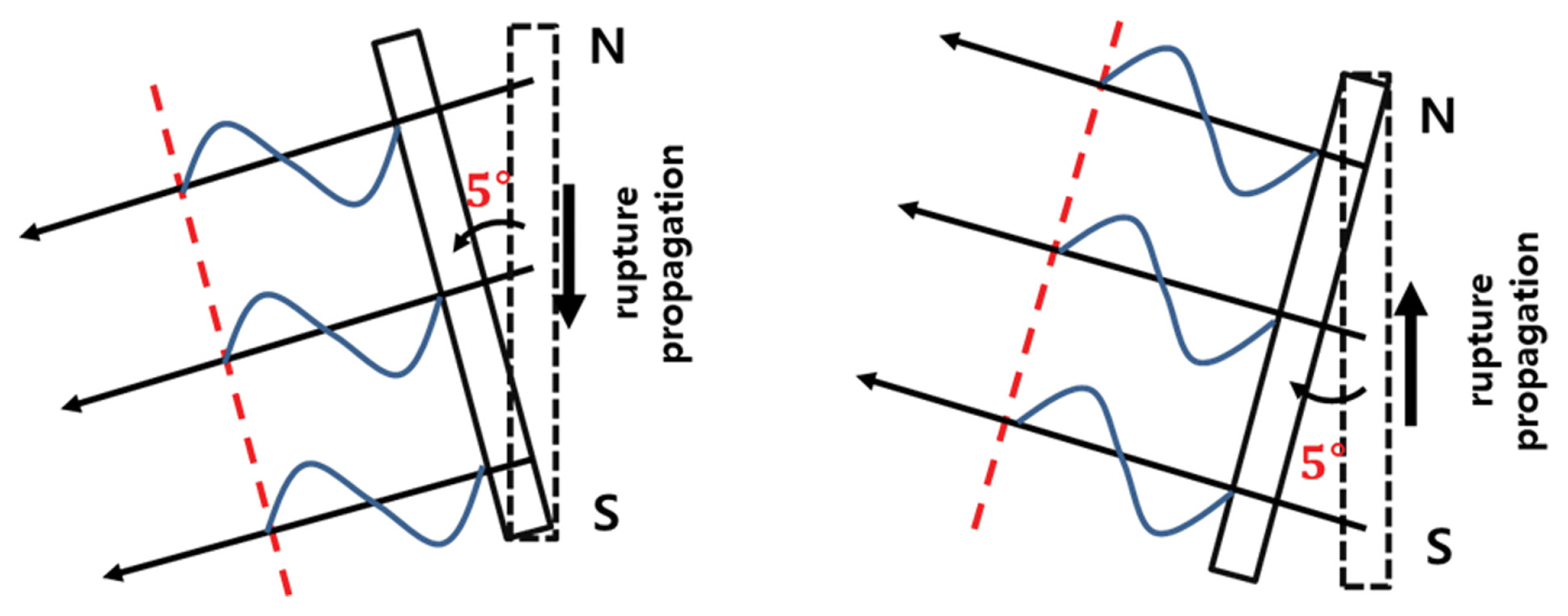
주향각 θ는 E1 단층에서 동경사(Fig. 18의 ①과 ③)의 경우 북쪽으로부터 시계방향으로 3o 기울어진 방향을 기준방향으로 하고, 서경사(Fig. 18의 ②와 ④)인 경우 183o를 기준방향으로 사용한다. E3 단층의 경우 동경사에 대해 20o , 서경사에 대해 200o이다. 이는 JSCE(2016)에서 추천하는 값으로서 지진원이 가까운 일본 해안에 대해 적용할 수 있다. 그러나 파원역에서 멀리 떨어진 우리나라 동해안의 경우 작은 주향각 변화에도 관심 지역에서의 지진해일고가 크게 변할 수 있으므로 주향각에 대한 불확실성을 고려할 필요가 있다. 따라서 일본에서 추천하는 기준방향으로부터 시계방향과 반시계방향으로 각각 5o씩 기울여 주향각의 불확실성을 고려할 수 있다. 주향각에 대한 불확실성은 물리적으로 단층의 주향각 자체가 구간마다 약간씩 달라지는 면도 있으나, 단층파괴가 전체 단층길이에서 동시에 발생하지 않고 어느 한쪽 끝에서 시작하여 다른 쪽으로 전파해 나가는 현실적인 시간의존형 단층 파괴를 고려하기 위한 목적으로도 사용된다. 이 경우 지진해일의 전파방향은 단층폭 방향과 달라지며 Fig. 20에 보인 바와 같이 주향각의 변화로 이를 대체할 수 있다. 이 주향각 변화에 대한 로직트리 분기는 JSCE(2016)에서는 제시하고 있지 않으나 Sugino et al.(2015)의 연구 등에서 자주 채택되는 불확실성이며, 실제 단층파괴 전파과정을 시간의존형으로 복잡하게 해석하지 않고서도 종래의 동시파괴 모델을 이용하여 이를 쉽게 고려할 수 있는 장점이 있다.
2.3.2 류큐 트렌치
류큐 트렌치는 필리핀해판이 유라시아판 밑으로 섭입되면서 형성되었다. 따라서 지진발생 특성도 동해 동연부에서 발생하는 지진과는 매우 다르다. 전술한 바와 같이 섭입대에서 발생하는 지진은 응력강하량 모델을 적용하며, 스케일링 법칙은 지진규모 및 재현기간 분석에서 제시한 바와 같이 다음 식(1)과 식(2)를 적용한다.
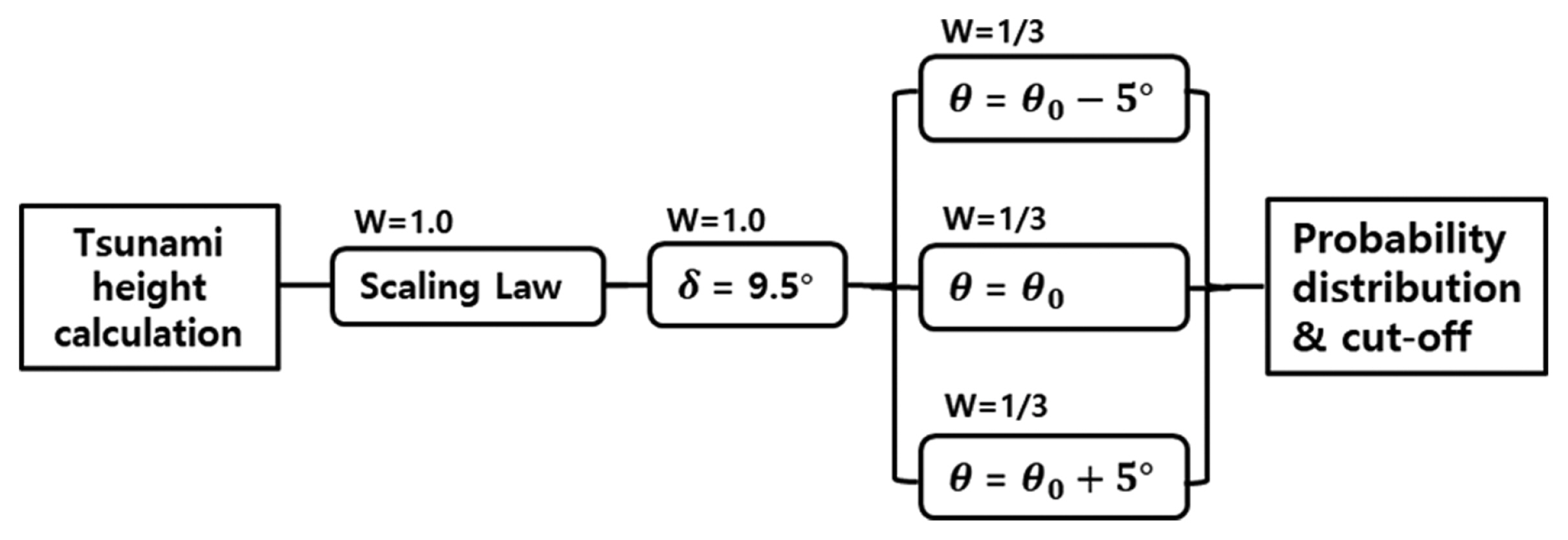
섭입대는 압축력을 받아 발생하는 역단층과 달리 단층 파괴면이 상부 판과 하부 판 사이의 섭입면에 위치하여 경사각이 일정하며, 류큐 트렌치의 경우 δ = 9.5o로 알려져 있다. 단층면의 주향각 θ는 트렌치의 방향과 일치하나, 단층 파괴의 전파 과정을 고려하기 위해 동해 동연부에서와 같이 ±5o의 분기를 고려하였다.
류큐 트렌치 지진의 규모는 역사지진 분기에 대해 Mw 7.8 ± 0.2(단층면적 S = 9,900 km2)과 대규모 상정지진 분기에 대해 Mw 8.3 ± 0.2(단층면적 S = 30,000 km2)로 정한 바 있다. 응력강하량 모델에 적용하는 스케일링 법칙인 식(1)에서는 지진규모에 따른 단층면적 S만 주어지고, 단층면의 폭과 길이는 주어지지 않으므로 이를 별도로 정해야 한다. 일본의 지진조사연구추진본부(HERP, 2013)에 따르면 류큐 트렌치에서 발생하는 지진에 대해 Fig. 22에 보인 바와 같이 규모별 단층면 형상이 제시되어 있다. Fig. 22에 제시된 L = 90 km, W = 90 km의 면적에 응력강하량 모델을 적용할 경우 전술한 바와 같이 기왕최대규모 Mw 8.0이 고려되지 않으므로 면적을 증가시켰으며, 역사지진의 단층면적(S = 9,900 km2)에 대해 L = 110 km, W = 90 km를 설정하였다. 대규모 상정지진의 단층면적(S = 30,000 km2)은 L = 200 km, W = 150 km로 설정하였다.
류큐 트렌치 지진파라미터는 Fig. 14에 주어진 류큐 트렌치 로직트리의 경로에 따라 선택된 단층의 면적과 응력강하량을 식(1)을 사용하여 결정한다. 예를 들어 3.0 MPa의 응력강하량과 단층활동면적 30,000 km2에 대하여 M0는 6.399 × 1021 (= 16/7 × 3 × 106 × 30,000 × 106 /π)1.5이고, 이에 대한 규모는 8.47이다. 단층의 활동변위량은 동해 동연부 지진파라미터 산정과정의 식(7)을 이용하여 결정된다. 류큐 트렌치의 지진발생부는 20km 미만의 얕은 곳에서 위치하므로(Arai et al., 2016) 류큐 해구의 강성률은 μ = 3.5 × 1010 N/m2를 적용하였다.
선단부 지진에 대해서는 JSCE(2016)에서 제시한 방법에 근거하여 응력강하량 모델이 아닌 스케일링 규칙을 통해 단층 파라미터를 결정하였으며, 스케일링 규칙 2가 단층길이를 과도하게 길게 평가하는 점을 착안하여 스케일링 규칙 1(JSCE, 2011)을 사용하였다. 단층의 폭 W는 일본토목학회(JSCE, 2016)에서 제시한 바와 같이 50 km로 고정하였다. 단층 파라미터의 결정과정은 동해 동연부 지진 파라미터 결정과정과 동일하다. Fig. 23은 류큐 트렌치에서 발생하는 지진에 대한 해일고 추정모델 로직트리 분기를 보여준다.
2.4 지진해일고 확률분포의 표준편차 및 타절범위
주어진 지진에 의한 초기 수면변위를 이용하여 지진해일 전파 수치모의를 수행하고 관심 지점에 대한 수위의 시계열을 구한 다음, 시계열 상의 최대치를 취하여 해일고의 확률 분포를 구한다. 이는 해일 전파 수치모의 과정에서 발생하는 다양한 오차를 고려하기 위함이다. 확률분포의 확률밀도 함수는 해일고 최대치 H0를 중앙치로 하는 정규대수분포로 가정하고 확률분포의 불확실성 고려를 위한 표준편차와 타절범위를 정한다. 대수정규분포의 확률밀도함수는 다음 식 (12)와 같다.
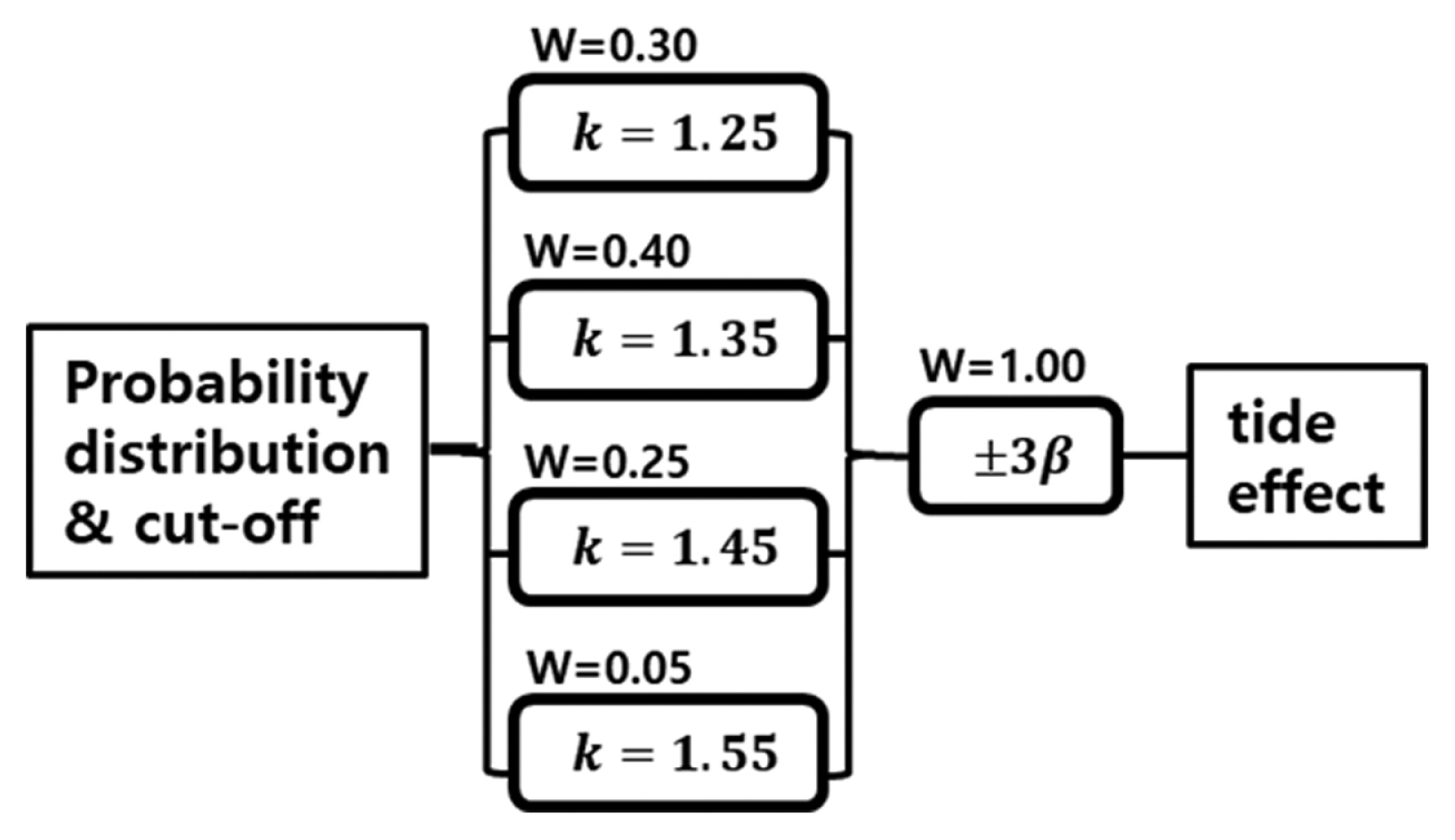
여기서 μ는 해일고 최대치 H0의 자연대수치, 즉 μ = lnH0이다. 또한 β = lnκ로서 κ는 표준편차이다. 중앙치 H0로부터 차이가 매우 크거나 작은 해일고에 대해 식(12)로 확률을 구하면 매우 작은 값을 가지는 바, 현실적으로 발생할 가능성이 없다고 간주하여 타절(cut-off)한다. JSCE(2016)에서는 중앙치로부터 ± 3β를 타절범위로 추천하고 있다. Fig. 24는 최대해일고의 확률분포와 타절을 고려하기 위한 로직 분기와 그 가중치를 보여준다.
3. 로직트리의 작성
전술한 로직트리의 구성 요소들을 조합하여 로직트리를 작성한다. 로직트리의 분기는 단일 사상의 불확실성을 분기로 고려하는 것이므로 어느 1가지 분기가 발생하면 다른 분기는 발생할 수 없다. 따라서 각 분기의 가중치 합은 1이다. 반면 지진원의 위치는 각각의 진원이 독립적으로 거동하므로 여러 지진원에서 지진이 동시에 발생할 수도 있다. 그러므로 분기로 처리하지 않고 각각의 확률분포의 합으로 처리한다.
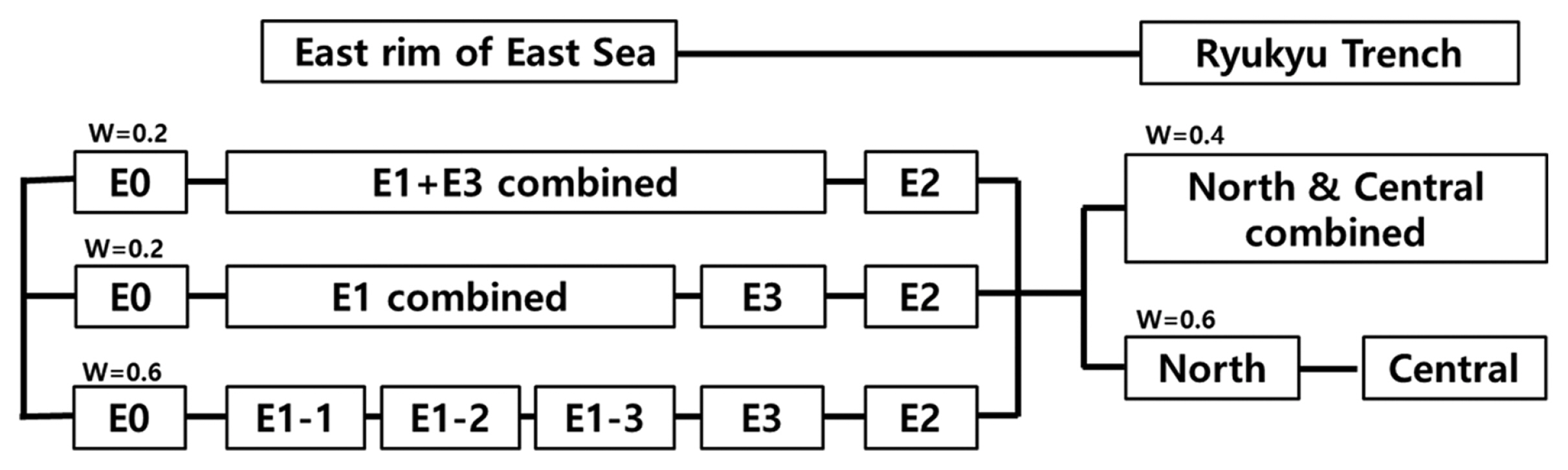
Fig. 25는 동해 동연부 지진원과 류큐 트렌치 지진원에 대한 전체 로직트리를 보여주며, Fig. 25에 제시된 지진원별 일체 및 단독 거동에 관한 분기에 부여된 가중치는 공식적으로 연구된 사례가 없다. 일본토목학회(JSCE, 2016)에서는 일본 해구나 난카이 트러프에 대한 로직트리에서 세그먼트가 서로 연동하여 거동하는 경우에 비하여 단독으로 거동하는 경우에 상대적으로 높은 가중치를 부여하였다. 따라서, 본 연구에서는 단독 거동 분기에 절반 이상인 0.6의 가중치를 부여하였으며 잔여 가중치를 남은 분기에 균등하게 부여하였다.
각 지진원의 개별적인 로직트리는 대표적으로 동해 동연부의 E1-1 세그먼트에 대해서만 상세한 종합 로직트리 분기를 Fig. 26에 제시하였다. 동해 동연부의 E1-1 세그먼트에 대한 로직트리를 살펴보면 지진규모 분기가 5가지이며, 모든 지진 규모 분기 각각에 대해 재현기간이 3가지 경우로 분기하고, 각각의 재현기간에 대해 스케일링 법칙이 2가지로 분기한다. 각각의 스케일링 법칙 분기에서 경사각이 3가지로 분기한다. 다른 구성요소에 대한 분기도 같은 방법으로 연결된다. 따라서 E1-1 세그먼트의 총 분기 수는 지진규모 5가지, 재현기간 3가지, 스케일링 법칙 2가지, 경사각 3가지, 경사각 위치 4가지, 주향각 3가지, 단층변위분포(asperity) 4가지, 해일고 추정치 편차 4가지, 타절범위 1가지의 조합을 고려하면 5 × 3 × 2 × 3 × 4 × 3 × 4 × 4 × 1 = 17,280개의 분기가 고려된다.
E1-1 영역의 17,280개의 각 분기마다 다음 영역인 E1-2 세그먼트의 17,280개 분기가 연결되므로 E1-1영역과 E1-2영역 2개만을 고려할 경우 17,280 × 17,280 = 298,598,400개의 분기가 형성된다. 만약 동해 동연부 지진발생 영역 모두를 고려하면(즉, Fig. 25의 동해 동연부 3가지 주요 분기 중 각각의 세그먼트를 따로 고려하는 맨 아래 줄의 분기만을 고려하면) E0, E1-1, E1-2, E1-3, E2, E3의 총 6개 영역으로 분할되어 있고, 각 영역이 E1-1처럼 17,280개의 로직트리 분기를 가지므로 총 로직트리의 분기는 17,280 × 17,280 × 17,280 × 17,280 × 17,280 × 17,280 = 2.66×1025개의 분기가 형성된다. 각 분기마다 1개의 재해도 곡선이 산출되므로 2.66 × 1025개의 재해도 곡선을 계산하고, 이들을 조합하기 위해서는 고속의 대용량 슈퍼컴퓨터로도 계산이 불가능할 정도로 분기의 수가 많다. 따라서 로직트리의 단순화가 필요하다. 가장 손쉬운 단순화 방법은 관심 해역에 미치는 지진해일 영향이 상대적으로 작은 지진원 분기를 제외하거나 가중치가 작은 불확실성 분기를 생략할 수 있다. 그러나 이 경우 연초과확률이 높은(다시 말해 재현기간이 짧은) 해일고가 과소 평가될 수 있다. 다른 방법으로는 이미 생성된 원래의 로직 분기에서 Monte Carlo 난수에 의해 무작위로 계산 가능한 범위의 분기 수만큼을 추출하여 분석하는 방법이다. Jho et al.(2019)는 JSCE(2016)가 제시한 Monte Carlo 무작위 추출법을 적용하고 그 효용성을 확인한 바 있다.
4. 결 론
본 연구에서는 우리나라 남동 해역에 위치하는 중요 시설물에 대한 확률론적 지진해일 재해도 분석에서 자연현상의 불확실성을 고려하기 위해 로직트리를 작성하였다. 우리나라 남동 해역에서 피해를 유발하는 지진해일의 지진원으로 동해 동연부 단층대와 류큐 트렌치의 섭입대 단층 특성을 파악하여 로직트리에 반영하였다. 동해 동연부 단층대에 대한 로직트리는 일본 토목학회 보고서 등에 자세히 제시되어 있다. 그러나 지진원이 매우 가까운 근지 지진해일에 주안점을 둔 일본의 로직트리에는 원거리 전파 시 문제가 될 수 있는 몇 가지 단층 거동 특성에 대한 고려가 미비되어 있다. 본 연구에서는 Jho et al.(2019)에서 제안한 바와 같이 우리나라 해역에서 문제를 일으키는 지진해일의 대부분이 원거리 전파 지진해일이므로 단층의 주향각에 대한 불확실성을 추가하였다. 또한 일본의 최근 보고서에서 채택한 스케일링 법칙은 지진규모 Mw 7.7 이상의 지진에 대해 단층변위량이 포화치로 일정해진다. 따라서 큰 지진규모에 대해서는 단층길이가 지나치게 길어져 세그먼 트 길이를 초과하는 경우가 발생한다. 본 연구에서는 이러한 불합리한 점을 고려하여 이전 일본 보고서에서 채택된 변위 최대치 제한이 없는 스케일링 법칙을 추가로 고려하는 로직트리 분기를 설정하였다. 류큐 트렌치 섭입대 단층에 대해서는 일본에서도 중요 지역에서 제외되어 로직트리가 제시된 바 없다. 본 연구에서는 류큐 트렌치와 인접한 난카이 트러프와 일본해구의 섭입대 지진해일 재해도 평가를 위한 로직트리를 참고하여 수립하였다. 본 연구에서 수립된 로직트리는 우리나라 남동해안 지형과 지진원의 특성 및 불확실성 등을 고려하여 이 해역에 위치하는 중요 시설물에 대한 지진해일 재해도 평가의 기본 틀을 제시하였다는 점에서 가치가 있으며, 후속 연구자들의 이해를 돕기 위해 불확실성을 고려하기 위한 분기 방법 및 각 분기에 부여되는 가중치 설정 방법 등에 대해 자세한 과학적 설명을 제시하였다는 점에서도 의미가 있다.