요약본 연구는 제주도 남서부 해역의 표류체 이동 예측을 위해 2020년 8월 제주도 남서부 5개 지점에서 투하된 표층 뜰개 위치자료와 수치모델 예측자료를 학습자료로 이용한 인공지능 기반 입자추적 모델 5개를 구축하였다. 구축된 AI 기법은 기계학습 3종(Extra Trees, LightGBM, Support Vector Machine)과 딥러닝 2종(DNN, RBFN)이다. 또한 해수유동 수치모델 입자추적 예측자료 1종 및 AI 기법 입자추적 예측자료 5종을 표층 뜰개 관측자료와 비교하여 각 예측모델별 예측 정확도를 평가하였다. 6종 모델의 예측 정확도를 평가하기 위해, 5개 정점에 대한 3개 스킬량(MAE, RMSE, NCLS)의 평균값을 비교 검토하였다. 최종적인 결과로서 딥러닝 DNN 모델이 MAE, RMSE, NCLS에서 다른 모델보다 가장 우수하게 나타났다.
AbstractPositions of five drifting buoys deployed on August 2020 near southwestern area of Jeju Island and numerically predicted velocities were used to develop five Artificial Intelligence-based models (AI models) for the prediction of particle tracks. Five AI models consisted of three machine learning models (Extra Trees, LightGBM, and Support Vector Machine) and two deep learning models (DNN and RBFN). To evaluate the prediction accuracy for six models, the predicted positions from five AI models and one numerical model were compared with the observed positions from five drifting buoys. Three skills (MAE, RMSE, and NCLS) for the five buoys and their averaged values were calculated. DNN model showed the best prediction accuracy in MAE, RMSE, and NCLS.
1. 서 론현재 우리나라에서는 유동방정식에 기반을 둔 해양수치모델을 이용하여 해류, 표류체 이동 예측, 유류확산과 같은 오염물질 방재 및 해난 사고에 따른 수색구조 등에 활용하고 있으나, 이 같은 고전적인 수치모델 기반 해수유동 예측은 고성능 서버에서도 수 시간이 소요되는 단점이 있다. 반면, 인공지능 기법은 한번 학습이 되면 새로운 예측 결과를 수 분만에 도출할 수 있는 장점이 있기 때문에 최근 인공지능 기반 예측 모델이 빠르게 출현하고 있다(Ha et al., 2022).
최근 2020년 전후로 인공지능(기계학습 및 딥러닝) 기법을 이용한 표류체 이동 경로 예측에 대한 연구가 본격적으로 이루지고 있다. Lee et al.(2017)은 관측된 바람자료와 표층 뜰개의 이동경로를 5개 기계학습 기법으로 학습 후 뜰개 이동 경로 예측 모델을 제안하였다. Kim and Kim(2018)은 표층 뜰개 자료를 수집할 때 발생하는 오측 및 결측을 보정하기 위한 방법으로 순환신경망 기법을 제시하였다. Seo(2021)는 위성 뜰개가 관측한 바람 및 해류 데이터에 파생 변수로 바람 및 해류 방향을 생성하여 성능 개선을 연구하였다. Ha et al. (2022)는 연안에서 관측한 조위와 바람 자료를 이용한 기계 학습 기반 표류 예측모델을 제안하고 관측 자료와 표류 예측 모델 이동경로를 비교·분석 후 개선방안을 제시하였다.
하지만 관측된 자료의 수집영역의 한계, 수집기간 등을 고려하면 연안에서 멀어 질수록 학습할 수 있는 자료의 수가 줄어들어 입자추적 예측이 어렵다. 또한 실제 표류 위치와 수치모델의 오차, 예측영역이 육지와 가까운 경우 모의가 불가능한 문제 등의 당면과제를 가지고 있다. 특히 수치모델의 해상도를 향상시키거나 표층 뜰개 관측결과를 이용해 모델을 개선하는 방법이 진행되고 있으나 완전한 모의는 아직 불가능하기에 지속적인 관측 및 연구가 필요한 실정이다(Ha, 2021).
본 연구는 제주도 남서부 해역의 표류체 이동 예측을 위해 수치모델 예측자료를 학습자료로 이용한 인공지능 기반 입자 추적 모델 5개를 구축하였다. 구축된 AI 기법은 기계학습 3종(Extra Trees, LightGBM, Support Vector Machine)과 딥러닝 2종(DNN, RBFN)이다. 또한 해수유동 수치모델 입자추적 예측결과 1종과 해수유동 수치모델 결과를 학습한 AI 기법 입자추적 예측자료 5종을 현장 표층 뜰개 관측 자료와 비교하여 모델의 예측 정확도를 평가하였다. 현장 표층 뜰개 관측 자료는 제주도 남서해역 5개 지점(Fig. 1)에서 최근 2년(2020년~2021년) 동안 투하된 총 10개 표층 뜰개의 경로 관측 자료이다. 모델 예측 정확도 평가 방법은 5개 정점에 대한 3가지 스킬량(MAE, RMSE, NCLS)의 평균값을 기반으로 비교 검토하였다.
2. 재료 및 방법2.1 표층 뜰개 현장 관측자료본 연구에 사용된 표층 뜰개 관측 자료는 Fig. 1에 제시된 제주도와 이어도 해양과학기지 사이의 5개 정점이며, 2020년 7월 31일부터 10월 28일까지, 2021년 8월 19일부터 8월 23일까지 자료를 수집하였다. Table 1은 5개 정점별 표층 뜰개의 초기 투하 위치, 관측기간 및 획득된 자료의 수를 나타내고 있다. 수집된 자료의 좌표 간 속도와 거리를 고려하여 2-필터 기반 노이즈 제거 방식을 사용하였다(Kim and Park, 2012). 최종적으로 2020년에 수집한 표층 뜰개 자료(I-1~5)는 인공지능 기법의 학습자료(training set)로, 2021년에 수집한 자료(IE-1~5)는 입자추적 모델의 스킬 평가를 위한 검증자료(test set)로 활용하였다.
2.2 해수유동 기반 입자추적 모델2.2.1 수치모델 예측자료입자추적 모델의 입력자료와 인공지능 학습 자료를 생산할 수치모델은 국립해양조사원에서 운용 중인 ROMS 기반 3 km 해상도의 해수유동 수치모델(이하 ROMS)과 WRF 기반 4 km 해상도의 기상예측 수치모델이다. 수치모델에 관한 내용은 참고문헌(Byun et al., 2017)에 기술되어 있다. ROMS 모델에서는 해수유동 유속(U, V) 자료를, WRF 기반 기상예측 모델은 바람(U, V) 예측 자료를 활용하였다(Table 2).
2.2.2 자료의 해상도 차이 보정본 연구에서 사용한 수치모델의 경우 표층 뜰개 관측자료와 비교하였을 때 해상도에서 그 차이가 크다. 따라서 좀 더 세밀한 해수유동 및 바람 예측값을 얻기 위해 Shepard(1968)가 제안한 역거리 가중법(Inverse Distance Weighting, IDW)를 사용하였다. 이 기법은 관측 지점의 위치가 가까울수록 유사하다는 기본 가정을 요구하며 다른 공간보간기법에 비해 적용 방법이 단순하고 연산시간이 짧다는 장점이 있다. 자료의 시간 및 공간 해상도를 일치시키기 위한 선형보간과 역거리 가중법은 다음 식에 따른다.
여기서, yo는 알고자 하는 위치의 예측값을, yoi는 i번째 관측지점에 대한 관측값을 의미한다. di는 yo의 위치와 yoi 관측 지점 간의 거리를 의미한다. k는 값에 따라 거리에 대한 영향력을 조절할 수 있으며, 본 연구에서는 William and James (1978)이 제시한 k = 2를 사용하였다.
2.2.3 입자추적 예측모델입자추적 예측모델은 초기장으로 주어지는 임의의 위치에서 가장 가까운 격자 위치를 찾은 후 해수유동성분을 계산하여 경과시간 δt에 의해 다음 식과 같이 새로 놓이게 될 위치를 계산한다.
여기서, U0와 V0은 위치 X0, Y0와 가장 가까운 격자이며, 바람의 영향이 고려된 해수유동 예측 수치모델의 유속이다. 위 식을 이용하여 초기 입력위치, 수치모델의 모의 간격, 입자추적 모의 시간을 입력하면 초기 위치로부터 입력한 모의 시간까지의 유속과 위치를 계산할 수 있다(Kämpf, 2009; Ha et al., 2022).
2.3 인공지능(AI) 기반 입자추적 모델2.3.1 기계학습 알고리즘① Extra Trees(ET)ET는 여러 개의 Decision Tree(DT)로 이루어진 앙상블 알고리즘이며, Random Forest(RF)가 변형된 알고리즘이다. DT는 일련의 예/아니오 질문을 통해 자료의 분류 혹은 회귀 결정에 이르는 모형이다. DT는 비교적 이해하기 쉽고 시각화가 용이한 방법이지만, 훈련단계에서 과적합(overfitting)되는 경향이 있어 일반화 성능이 좋지 않다(Hahm et al., 2019). 따라서 DT의 과적합을 줄이기 위해 RF는 복원추출한 학습 자료를 사용하여 여러 개의 서로 다른 DT를 만들고, DT의 결과를 평균한다. ET는 이러한 RF가 변형된 알고리즘으로 트리가 분지할 때 변수(feature)를 무작위로 선정하여 폭넓은 시각으로 변수들을 평가할 수 있게 해준다. ET는 RF보다 무작위성이 증가하여 과적합의 위험이 적고, 연산량이 적어 속도가 훨씬 빠르다는 장점이 있다(Geurts et al., 2006).
② LightGBMLightGBM은 여러 개의 DT로 이루어진 앙상블 알고리즘이며, 그래디언트 부스팅(Gradient Boost Machine, GBM) 알고리즘의 일종이다. 트리가 서로 독립적으로 생성된 ET와는 달리, LightGBM은 순차적으로 생성되면서 이전 트리가 틀리게 예측한 자료에 대해 가중치를 부여하여 학습한다. 이렇게 순차적인 학습을 통해 오차를 보완해가는 알고리즘을 부스팅(Boosting)이라고 하며, 가중치 업데이트에 경사하강법(Gradient descent)을 이용하는 것이 GBM 알고리즘이다. GBM 기반 트리 앙상블 모델인 XGBoost, LightGBM, CatBoost는 캐글(kaggle) 대회에서 상위권 참가자들이 자주 사용하는 알고리즘으로 알려져 있다. LightGBM은 트리 성장 방식으로 수평적 성장(Leaf-wise growth) 방식을 이용하는 것이 특징이며, 이로 인해 트리가 불필요하게 커지지 않아 모델이 가볍고 학습시간이 매우 빠르다. 그러나 과적합이 발생하기 쉬우므로 적정한 하이퍼파라미터(Hyperparameter) 튜닝을 통해 과적합을 방지해야 한다(Ke et al., 2017).
③ Support Vector Machine(SVM)SVM은 다차원 공간에 초평면(hyperplane) 또는 초평면들의 집합을 형성하여 분류 혹은 회귀를 수행한다. 분류 모델의 경우 초평면이 자료를 분류하는 경계선이 되어, 초평면과 자료 사이의 최소 거리인 마진(margin)이 최대가 되는 초평면을 찾으며, 회귀 문제의 경우 분류와 반대로 일정 마진 내에 가능한 많은 자료를 포함하도록 하는 초평면을 구한다. SVM은 입력 공간에서 자료가 선형적으로 분류 및 회귀가 어려울 때 커널함수(kernel function)를 사용하여 입력공간의 자료를 고차원의 특징 공간으로 재배치함으로써 선형적인 분류 및 회귀가 가능하도록 한다(Vapnik, 2000; Sim et al., 2009). SVM은 중소규모의 다양한 자료 해석에 좋은 성능을 보여주지만, 세심한 자료의 사전 준비와 변수 조율이 필요한 단점이 있다(Hahm et al., 2019).
2.3.2 딥러닝 기법 알고리즘① Deep Neural Network(DNN)DNN은 입력층과 출력층 사이에 두 개 이상(deep)의 은닉층이 존재하는 인공신경망 기법을 의미한다. 인공신경망은 수 많은 뉴런(neuron)으로 구성된 인간의 뇌가 뉴런의 자극에 의해 정보를 전달하며 자료를 학습하고 분석하는 방법을 모방하였다. 인공신경망의 은닉층에는 뉴런의 역할을 담당하는 다수의 노드(node)가 존재하며, 학습을 통해서 각각의 노드에 적절한 가중치를 부여한다(Chun et al., 2020). 가중치 업데이트는 경사하강법을 사용하여 최적화되며, 오차를 출력층에서 입력층으로 역방향으로 가중치를 조정하는 역전파(back-propagation) 방식을 사용한다(Sze et al., 2017).
② Radial Basis Function Network(RBFN)
RBFN은 여러 학습자료를 군집화하여 군집중심을 방사형 기반 함수를 통해 고차원의 공간으로 변환하고 최적 가중치를 구하여 신경망 모델링을 구축하는 방법이다(Kim and Kim, 2017). RBFN은 한 개의 은닉층을 가지며, 입력층과 은닉층, 출력층의 구조로 이루어진다. 입력층과 은닉층 사이에는 가중치가 없고, 은닉층에서는 방사형 기반 함수를 사용하며, 출력층은 선형 출력층(Linear output layer) 구조를 갖는다. MLP (Multi-Layer Perceptron)가 스칼라곱(Dot product)을 기반으로 유사도를 측정하는 반면에, RBFN은 유클리드 거리(Euclidean distance)를 기반으로 유사도를 측정한다. 또한 비선형함수로 시그모이드함수(Sigmoid function, S자형 함수)나 하이퍼볼릭 탄젠트 함수 대신 가우시안 함수(Gaussian function)를 사용한다. 이로 인해 RBFN은 MLP보다 모델의 수렴속도가 빠르며 간단한 구조를 가진다.
2.3.3 인공지능 예측 모델 구축앞서 언급한 기계학습 3종(ET, LightGBM, SVM), 딥러닝 2종(DNN, RBFN)의 알고리즘을 사용하여 5개의 인공지능 기반 입자추적 예측모델을 구축하였다. 인공지능 모델은 경위도 좌표를 변환시킨 X, Y 좌표, 역거리 가중법을 적용한 수치모델 ROMS 및 WRF의 해수유동 예측 자료(U, V), 바람 자료(U, V)를 입력변수로 사용하여 X, Y의 변화량을 예측한다. 학습데이터의 기간과 모델 입력 및 출력 변수는 Table 3에 제시된 바와 같다. 인공지능 예측 모델은 30분 뒤 위치를 예측하여 출력하고, 그 위치는 다시 모델의 입력변수로 사용된다. 이 과정은 예측하고자 하는 시간만큼 반복하여 최종적인 입자의 이동경로를 도출한다.
본 연구에서는 전술한 바와 같이 2020년에 관측한 표층 뜰개 자료를 학습자료로, 2021년 자료를 비교·검증자료로 활용하였다. 스킬 평가를 위한 검증데이터의 초기 위치는 Table 4와 같이 선정하였으며, 구축한 5개의 인공지능 모델의 성능을 비교하였다.
기계학습과 딥러닝 모델을 구현하기 위해서 각각 사이킷런(scikit-learn) 1.0.1과 텐서플로우(tensorflow) 2.3.0 버전을 포함하는 케라스(keras) 2.4.0 라이브러리를 사용하였고 개발언어는 Python 3.7을 이용하였다. 5개 모델의 하이퍼파라미터(Hyperparameter)는 Table 5와 같이 설정하였다.
2.4 관측 결과를 이용한 스킬 평가본 연구에서는 현장 표층 뜰개 관측 자료와 입자추적 예측모델의 결과를 비교하기 위해 각 자료들의 시간간격을 1시간으로 재추출한 뒤 3가지 스킬 평가(MAE, RMSE, NCLS)를 수행하였다. 먼저 식(7)의 MAE(Mean Absolute Error)은 예측값 Pi와 관측값 Oi의 차를 절대값으로 표시하고 그 값들을 합하여 관측된 수만큼 나누는 방법이다.
다음으로 식(8)의 RMSE(Root Mean Squared Error)은 정량적으로 예측값 Pi와 관측값 Oi 사이의 차이를 표시하는데, 제곱근 방식을 사용함에 따라 편차가 심할수록 그 값이 커진다.
마지막으로 식(9)와 식(10)의 NCLS(Normalized Cumulative Lagrangian Separation)은 Liu and Wiesberg(2011)이 제안한 표층 뜰개 이동 예측평가 방법이다.
여기서, di는 관측지점과 모델의 거리차를 나타내며 loi는 관측치 이동거리의 누적합, N은 자료의 수, n은 임계치를 나타낸다. NCLS에 사용되는 임계치 n은 모델을 평가하는 영역과 수준에 따라 임의로 조절할 수 있으며, SS 값이 1에 가까울수록 모의를 완벽하게 한 것으로 판단할 수 있다(Table 6). 본 연구에서는 참고문헌(Lee et al., 2017)에서 제시한 n 값을 1로 설정하여 적용하였다(Ha et al., 2022).
3. 결과 및 고찰3.1 입자추적 모델의 스킬 평가본 연구에서의 입자추적 모델의 스킬 평가의 최종 결과는 Table 7에 제시하였다. 계산 결과에서 평균값은 소숫점 3자리에서 반올림하였다.
먼저, ROMS 수치모델의 스킬 평가 결과는 MAE 17.0 km, RMSE 14.44 km, NCLS 0.75이었다. 본 연구에서 구축된 기계학습 3종(ET, LightGBM, SVM) 중에서 Extra Trees(ET) 모델의 경우는 MAE 12.77 km, RMSE 10.40 km, NCLS 0.80이었으며, LightGBM 모델의 경우 MAE 12.92 km, RMSE 10.69 km, NCLS 0.79이었고 SVM 모델의 경우는 MAE 13.74 km, RMSE 11.43 km NCLS 0.80이었다. 또한 딥러닝 2종(DNN, RBFN) 중에서 DNN 모델의 스킬 평가 결과는 MAE 10.02 km, RMSE 8.43 km NCLS 0.84이었으며 RBFN 모델의 경우에는 MAE 18.29 km, RMSE 14.79 km NCLS 0.74로 나타났다(Table 7, Fig. 2).
RBFN을 제외한 나머지 모델의 MAE, RMSE가 X 변화량 보다 Y 변화량의 오차가 더 크게 나타났는데 이는 학습했던 ROMS 모델의 Y 방향 오차가 상대적으로 더 큰 영향을 따라간 것으로 볼 수 있다. 이는 본 연구에 사용된 ROMS 모델 한계를 보여줌으로써 향후 ROMS 모델 개선을 통한 정확도 향상이 필요할 것으로 사료된다.
최종적으로 6종류의 입자추적 모델 스킬 평과 결과에 따르면 Fig. 3에 제시된 바와 같이 인공지능 기반의 딥러닝 해석 모델인 DNN 결과가 NCLS가 0.84로서 가장 우수한 결과를 도출한 것으로 나타났다.
3.2 제주도 남서부 해역의 입자추적 예측 결과본 연구에서는 Table 7에 제시된 스킬 평가 가운데 가장 높은 예측 정확도를 나타낸 DNN 기반 입자추적 모델결과와 수치모델 ROMS 입자추적 모델결과 및 표층 뜰개 입자 추적 경로를 Fig. 4에 나타내었다. 정점 별 이동경로를 살펴보면 IE-1에서는 전체적인 이동경로가 비슷하게 나타난 것으로 보인다. IE-2에서는 관측자료는 제주도 서쪽 해안에 갇힌 모습을 보이나 DNN 기반 예측자료는 관측자료보다 북향하여 제주 북측으로 이동하였다. IE-3의 경우 이동경향과 거리가 과대 모의가 되는 경우가 나타났고, IE-4, IE-5에선 관측치에 비해 Tidal Jumping 경향이 과대하게 나타난 것으로 보인다.
전체적으로 볼 때 해수유동 수치모델에 비해 DNN 모델이 실제 표층 뜰개 이동 경로와 유사한 경향을 보이고 있음을 알 수 있다. 하지만 일부 정점에서 Tidal Jumping 현상 모의가 다소 부정확한 모습을 보인다. 이는 입자추적 모델이 조석 잔차 또는 항류 성분을 제대로 모의하지 못하고 있는 것으로 생각된다. 따라서 이를 개선할 방법으로는 학습자료 중 해수유동과 바람뿐만 아니라 풍파에 의한 Stokes drift 등 추가적인 인자를 고려해 볼 필요가 있을 것으로 사료된다.
4. 요약 및 결론본 연구는 제주도 남서부 해역의 표류체 이동 예측을 위해 2020년 8월 제주도 남서부 5개 지점에서 투하된 표층 뜰개 위치자료와 해수유동 수치모델 예측자료를 학습시킨 인공지능 기반 입자추적 모델을 구축하고 해수유동 수치모델 기반 입자추적 모델과 비교, 분석하였다. 본 연구 결과를 요약하면 다음과 같다.
1) 표층 뜰개 위치자료와 해수유동 수치모델 예측자료를 학습자료로 이용한 AI 기반 입자추적 모델 5개를 구축하였다. 구축된 AI 기법은 기계학습 3종(Extra Trees, LightGBM, Support Vector Machine)과 딥러닝 2종(DNN, RBFN)이다.
2) 해수유동 수치모델을 이용한 입자추적 예측 자료 1종과 AI 기법 입자추적 예측자료 5종을 현장 표층 뜰개 관측 자료와 비교하여 입자추적 모델의 스킬 평가를 수행하였다. 스킬 평가 방법은 5개 정점에 대한 3가지 스킬량(MAE, RMSE, NCLS)의 평균값을 비교 검토하였다. 최종적인 결과로서 딥러닝 DNN 모델이 3가지 스킬량에서 다른 모델보다 가장 우수하게 나타났다.
3) AI 기반 입자추적 모델에 의한 경로를 보면 수치모델 기반 입자추적모델이 경로를 과대 예측하는 현상을 크게 개선하였다. 반면, Tidal Jumping 현상에 대해서는 다소 부정확한 모습을 보인다. 이는 조석 잔차 또는 항류 성분을 제대로 모의하지 못하고 있는 것으로 보이며 이를 개선할 방법으로는 학습자료 중 해수유동과 바람뿐만 아니라 풍파에 의한 Stokes drift 등 추가적인 인자를 고려해 볼 필요가 있을 것으로 사료된다.
Fig. 4.Trajectories plotted by drifting buoys (black dot line), predicted by DNN particle tracking model (red dot line), and predicted by ROMS particle tracking model (blue dot line) for (a) IE-1, (b) IE-2, (c) IE-3, (d) IE-4, and (e) IE-5, respectively. 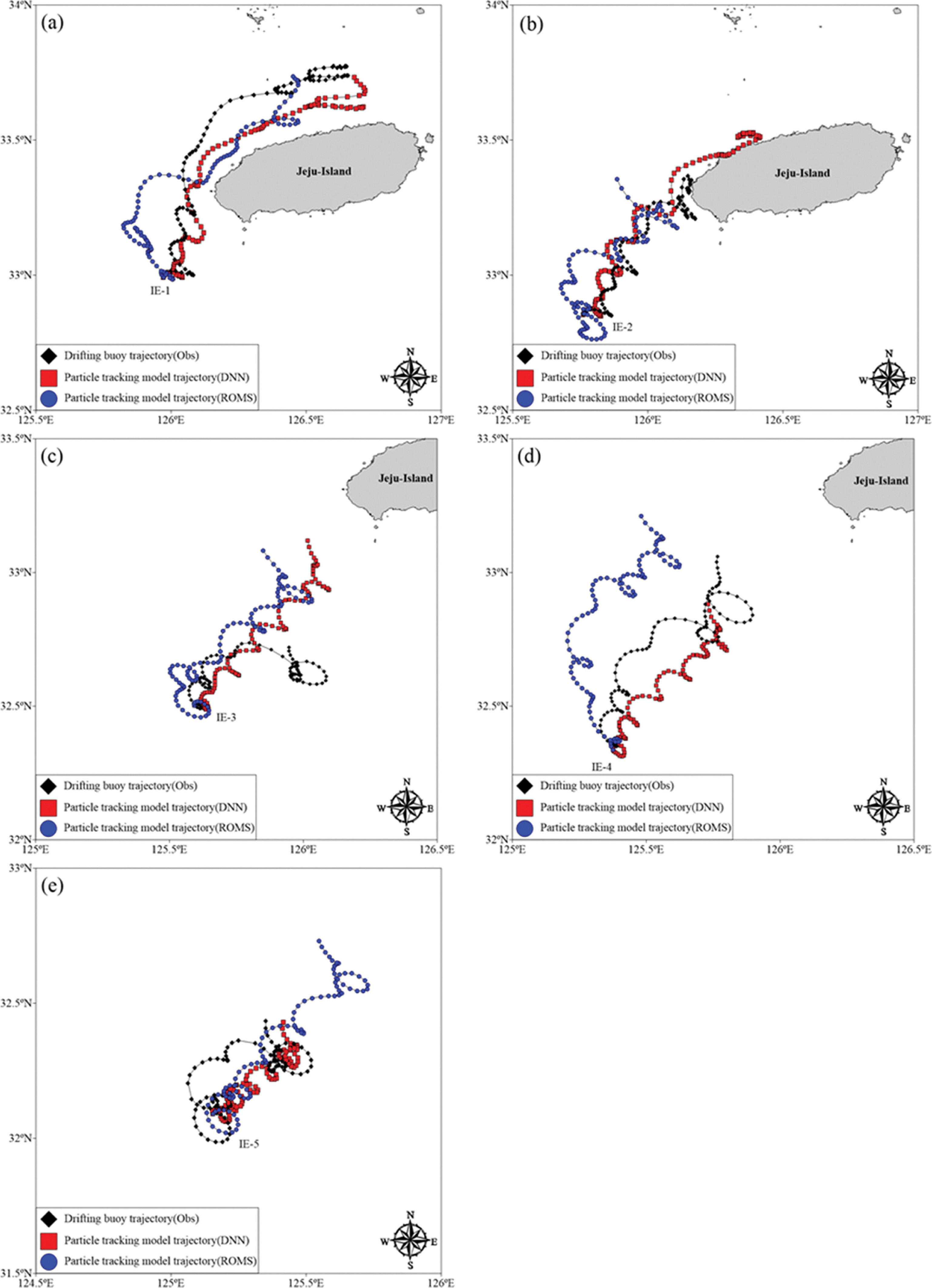
Table 1.Overview of collected drifting buoy data Table 2.Overview of two numerical models for producing input data of particle tracking model Table 3.Training data for particle tracking model
Table 4.Test data for skill evaluation Table 5.Hyperparameters for five AI models Table 6.Explanation of skill assessments Table 7.Skill evaluaion for six particle tracking models in the test set ReferencesByun, D.S., Seo, G.H., Park, S.Y., Jeong, K.Y., Lee., J.Y., Choi, Y.J., Shin, J.A., Choi, B.Y (2017). A Technical Guide to Operational Regional Ocean Forecasting Systems in the Korea Hydrographic and Oceanographic Agency(I): Continuous Operation Strategy, Downloading External Data, and Error Notification, Journal of Korean Society of Oceanography, 22(3):91-105 (in Korean)..
Chun, B., Lee, T., Kim, S., Kim, J., Jang, K., Chun, J., Jang, W., Shin, Y (2020). Estimation of DNN-based Soil Moisture at Mountainous Regions, Journal of The Korean Society of Agricultural Engineers, 62(5):93-103 (in Korean)..
Geurts, P., Ernst, D., Wehenkel, L (2006). Extremely randomized trees, Machine Learning, 63(1):3-42.
Ha, SY. (2021). A study on the trajectory prediction of drifting buoys considering machine learning methods in the Korea Strait, Pukyong National Univ.. Master’s thesis (in Korean)..
Ha, S.Y., Yoon, H.S., Kim, Y.T (2022). A Study on the Prediction of the Surface Drifter Trajectories in the Korean Strait, Journal of Korean Society of Coastal and Ocean Engineers, 34(1):11-18 (in Korean)..
Hahm, D., Park, S., Choi, S.H., Kang, D.J., Rho, T., Lee, T (2019). Estimation of Surface fCO 2 in the Southwest East Sea using Machine Learning Techniques, The Sea: Journal of the Korean Society of Oceanography, 24(3):375-388 (in Korean)..
Ke, G, Meng, Q, Finley, T, Wang, T, Chen, W, Ma, W, Liu, TY (2017). Lightgbm: A highly efficient gradient boosting decision tree, Advances in neural information processing systems, 30.
Kim, G.D., Kim, Y.H (2017). A survey on oil spill and weather forecast using machine learning based on neural networks and statistical methods, Journal of the Korea Convergence Society, 8(10):1-8 (in Korean)..
Kim, G.D., Kim, Y.H (2018). Correction of drifter data using recurrent neural networks, Journal of the Korea Convergence Society, 9(3):15-21 (in Korean)..
Kim, J.M., Park, Y.T (2012). GPS-based Noise Reduction Approach for Trajectory Recognition, J KIISE, 39(4):328-337 (in Korean)..
Kämpf, J. (2009). Ocean Modelling for Beginners (using open-source software). Springer, p 109.
Lee, C.J., Kim, G.D., Kim, Y.H (2017). Performance comparison of machine learning based on neural networks and statistical methods for prediction of drifter movement, Journal of the Korea Convergence Society, 8(10):45-52 (in Korean)..
Liu, Y, Weisberg, RH (2011). Evaluation of trajectory modeling in different dynamic regions using Normalized Cumulative Lagrangian Separation, Journal of Geophysical Research: Oceans, 116(C9).
Seo, J.H (2021). Prediction of Surface Drifter Trajectory Based On Feature Generation, Journal Title: Journal of The Korean Institute of Intelligent Systems, 31(4):299-304 (in Korean)..
Shepard, D. (1968). A two-dimensional interpolation function for irregularly-spaced data, In Proceedings of the 1968 23rd ACM National Conference. 517-524.
Sim, WS, Sung, SY, Cheng, CK. (2009). Performance analysis of Kernel function for support vector machine, In Proceedings of the IEEK Conference. The Institute of Electronics and Information Engineers, p 405-407 (in Korean)..
Sze, V., Chen, Y.H., Yang, T.J., Emer, J.S (2017). Efficient processing of deep neural networks: A tutorial and survey, Proceedings of the IEEE, 105(12):2295-2329.
Vapnik, V. (2000). The nature of statistical learning theory. Springer science & business media.
|
|
|||||||||||||||||||||||||||||||||||||||||||