1. 서론
현재 우리나라에서는 해양수치모델을 이용하여 해류 예측 및 표류체의 이동을 예측하여 유류 등 오염물질 확산, 해난 사고 인명구조 활동 등에 이용하고 있으나, 실제 표류 위치와 수치모델의 오차, 예측영역이 육지와 가까운 경우 모의가 불가능한 문제 등의 당면과제를 가지고 있다(Ha, 2021).
이런 문제점을 해결하기 위해 수치모델의 해상도를 높이거나 자료동화 기법을 적용하여 유동모델 자체의 정확도를 개선한 후 위성 뜰개 관측결과를 이용하여 표류예측 모델을 검증하는 등 표류예측 정확도를 개선시키려는 다양한 연구가 진행되고 있다. Ryu et al.(2002)은 2001년 12월~2002년 6월동안 사고로 표류한 파랑관측 부이에 대해 이동경로 해당 지역의 PODAAC(Physical Oceanography Distributed Active Archive Center) 바람 자료와 부이 이동경로에 대한 비교 연구를 수행한 바 있다.
수치모델 기반 해수유동 예측은 고성능 서버에서도 수 시간이 소요되는 반면, 인공지능 기법은 한번 학습이 되면 새로운 예측 결과를 수 분만에 도출 할 수 있는 장점이 있기 때문에 최근 인공지능 기법이 출현하고 있다. Lee et al.(2017)은 관측된 바람자료와 표층 뜰개의 이동경로를 5개 기계학습 (서포트벡터 회귀, 방사기저함수 네트워크, 가우시안 프로세스, 다층 퍼셉트론, 순환신경망) 기법으로 학습시킨 후 뜰개의 이동 경로 예측 모델을 제안하였다. 또한 Kim and Kim (2018)은 표층 뜰개 자료를 수집할 때 발생하는 오측 및 결측을 보정하기 위한 방법으로 순환신경망을 제시하고 15개 위성 뜰개(2015년 7개, 2016년 8개) 자료에 적용하여 13.9%의 자료를 보정하고 표류예측 모델의 성능을 1.4% 향상시켰다.
또한 현재 국립해양조사원에서는 2011년부터 해운 물류와 어업활동에 활용할 목적으로 인공위성 고도계 자료(Archiving, Validation and Interpretation of Satellite Oceanographic data, AVISO)를 사용하여 정밀도 높은 평균 표층 해류도를 제작하고 있는 중이며 최근 기계학습을 기반으로 한 자료학습 및 예측 분야의 과학기술이 발달함에 따라 해양 분야에서도 이를 접목하여 표층 뜰개의 이동경향을 모의하는 기초 연구가 진행되고 있다(Ha, 2021).
본 연구에서는 대한해협 연안에서 관측한 조위 및 바람 자료를 이용하여 기계학습기반 표류예측모델의 이동경로와 유동예측 수치모델기반 표류예측모델의 이동경로를 표층 뜰개 관측자료와 비교·분석하였다. 이동경로 예측 정확도를 3가지 방법(CC, RMSE, NCLS)으로 평가한 후 향후 개선방안을 제시하고자 하였다.
2. 재료 및 방법
2.1 자료 수집
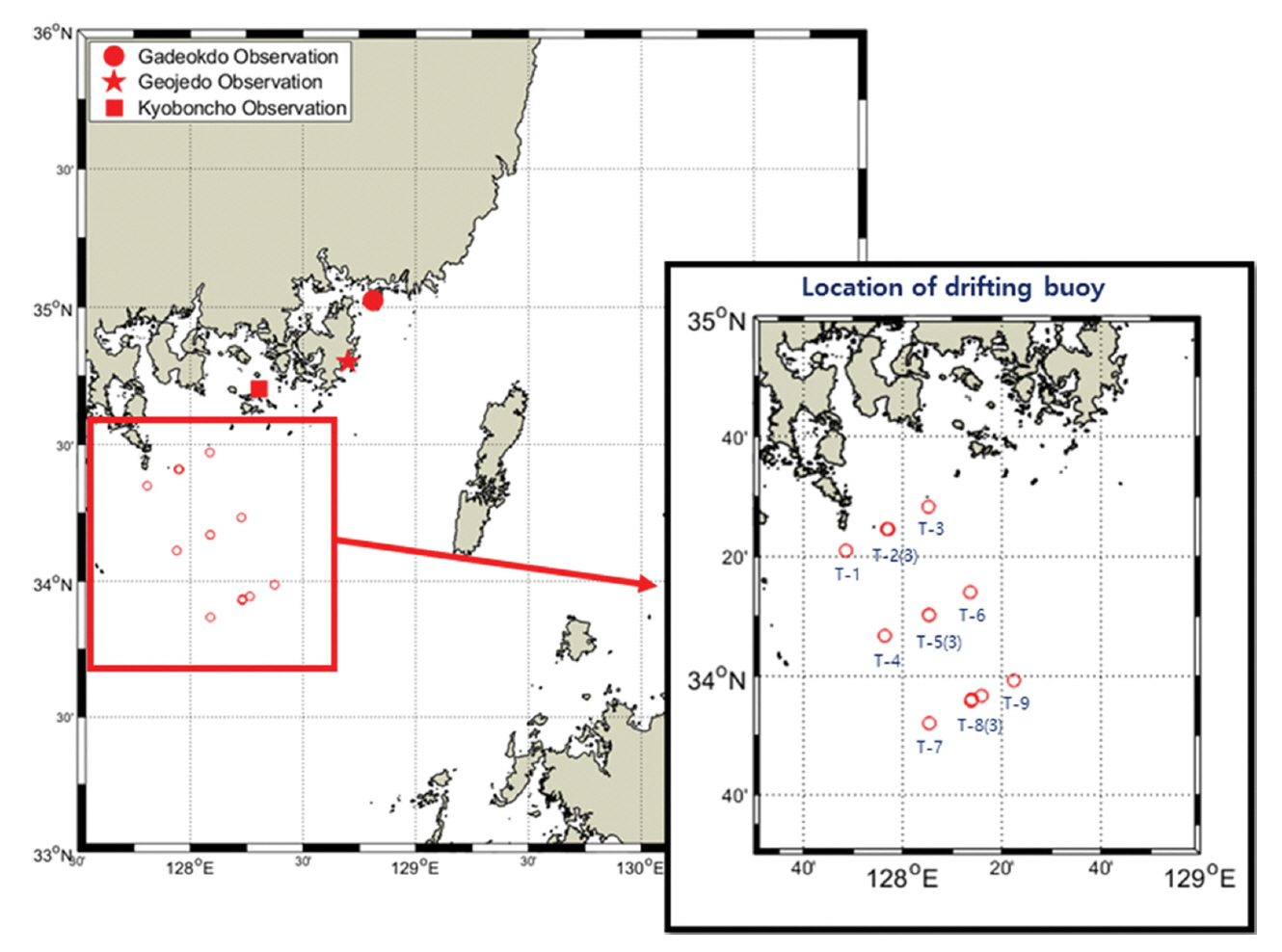
본 연구에서는 라그랑지 관측 방법인 표층 뜰개와 부이 추적 시스템을 이용하여 연안측에서의 해류장을 파악하고 단기 및 중·장기 관측을 통한 대한해협 및 동해의 전체적인 해류 공간 분포를 살펴보고자 하였다. 단기 관측으로 2020년 7월 21일부터 28일까지 총 9개 정점(T-1~T-9)에 15개의 표층 뜰개를 Fig. 1과 같이 투하하여 30분 간격으로 자료를 수집하였다. 특히 이 중 정점 T-2, T-5, T-8은 정점 내 약 200 m 간격으로 3개씩 연속 투하하였다. 표층 뜰개의 제원 및 투하 정점의 위치 자료, 현장실험 조건 및 전체 표층 뜰개의 이동 경로에 대한 보다 상세한 내용은 Ha(2021)의 문헌에 상세히 제시되어 있음을 밝힌다.
본 연구의 기계학습 훈련에 사용된 자료는 본 연구대상 해역인 대한해협과 인접한 국립해양조사원 관측소 중 조위와 바람(풍속, 풍향) 자료가 같이 수집되고 있는 교본초, 거제도, 가덕도 관측소 자료를 선정하였고 1시간 단위 자료로 변환 후 학습 자료로 사용하였다(Table 1, Fig. 1). 표층 뜰개 이동 경로는 자료 수신이 가장 양호했던 정점 T-5 이동경로를 학습 자료로 사용하였다(Table 2 및 Fig. 2). 자료수집기간은 2020년 7월 22일부터 27일까지, 관측간격은 표층 뜰개의 관측 간격을 고려하여 1시간 단위 자료로 선별하였다.
2.2 기계학습 기법
기계학습(머신러닝, Machine learning)은 학습방법에 따라 지도학습과 비지도학습으로 나눌 수 있는데 본 연구에 사용된 기법은 지도학습을 통한 기계학습 방법을 바탕으로 연구를 진행하였다. 지도학습은 정답이 주어진 데이터를 이용하여 학습 후 테스트 데이터에 대한 미래 결과를 예측하는 방법을 말하며 이러한 방법은 예측방법에 따라 회귀와 분류로 나눌 수 있다. 본 연구에 사용된 상세 알고리즘은 다음과 같다.
선형 회귀(Linear Regression) 기법은 학습 자료의 특성과 분포를 가장 잘 나타낼 수 있는 임의의 직선 y = Wx + b에서 가중치 W와 바이어스 b를 구하는 방법이다. 경사하강법을 이용하여 가설과 실제 데이터의 차가 최소값을 갖도록 하는 가중치 W와 바이어스 b를 구한다. 기계학습에서는 손실 함수 값을 최소로 하는 것이 가장 중요하다. 이는 y = Wx + b 함수의 계산 값 y의 평균 오차가 가장 작다는 의미이며, 평균 오차가 작다는 것은 가중치 W와 바이어스 b가 학습자료의 특성과 상관관계를 가장 잘 나타낸다고 볼 수 있다(Park, 2020).
의사결정나무(Decision Tree) 기법은 스무고개의 알고리즘과 상당히 비슷하다. 주어진 입력값에 대해 여러 번의 질문을 통해 답을 찾는 방법이기 때문이다. 의사결정나무에서 사용한 앙상블 기법인 배깅(Bagging)은 Bootstrap Aggregation을 줄여 표현한 말이다. 이는 주어진 데이터를 동일한 크기로 랜덤 복원 추출하여 생성한 후 데이터 별로 최대나무를 생성하고, 편향된 최대 나무들의 예측을 투표 방식으로 결합하여 최종 예측하는 방식이다(Heo, 2020).
2.3 수치예측모델
본 연구에 사용한 해수유동 수치모델은 MOHID 기반 300 m 격자 수치모델(이하 MOHID)과 ROMS 기반 3 km 격자 수치모델(이하 ROMS)이다. 본 모델은 현재 국립해양조사원에서 운용 중으로 매일 72시간의 해수면 높이/수온·염분/해수유 동을 예측하는데 사용된다. 대한해협에서 수행한 표층 뜰개 관측 자료와 수치모델 결과를 비교하기 위해 2020년 7월 22일부터 27일까지 표층 해수유동(동방성분(U) 및 북방성분(V) 성분) 자료를 추출하여 사용하였다(Table 5).
또한 본 연구에 사용된 표류예측 모델은 MATLAB®기반으로 작성된 입자추적 모델이다. 적용 모델의 입자추적 기법은 식(1)~식(4)와 같이 초기장으로 주어지는 임의의 위치(X0, Y0)에서 가장 가까운 수치모델 격자 위치를 찾은 후 해수유동 성분(U0, V0)을 계산하여 경과시간 δt에 의해 새로 놓이게될 위치(XN, YN)를 계산한다.
여기서, U0와 V0는 위치 X0, Y0)와 가장 가까운 격자이며, 바람의 영향이 고려된 해수유동 예측 수치모델의 유속이다. 위의 식을 이용하여 초기 입력 위치, 수치모델의 모의 간격, 입자추적 모의 시간을 입력하면 초기 위치로부터 입력한 모의시간까지의 시간별 유속과 위치를 계산할 수 있다.
2.4 표층 뜰개 관측 결과와의 비교 방법
본 연구에서는 표층 뜰개 관측 자료와 입자추적 수치모델의 예측 결과를 비교하기 위해 3가지 오차평가방법을 적용하였다. 3가지 오차평가방법은 CC(Correlation Coefficient, 상관계수), RMSE(Root Mean Square Error, 평균제곱근오차), NCLS(Normalized Cumulative Lagrangian Separation)이다 (Kim and Yoon, 2011).
상관계수(Correlation Coefficient, CC)는 식(5)와 같다.
여기서, Si는 i번째 예측값, Oi는 i번째 관측값, n은 모의자료의 개수다. 식(5)는 예측값과 관측값의 상관관계를 나타내주는 방법으로 CC 값이 1일 때 예측치와 관측치가 완벽하게 일치함을 나타낸다. 그리고 그 값이 0 이하일 경우 예측값과 관측값이 서로 상관관계가 없음을 나타낸다(Table 6).
식(6)은 정량적으로 관측값과 예측값 사이의 차이를 표시하는데, 특히 제곱근방식을 사용함에 따라 오차의 편차가 심할수록 그 값들이 커진다(Table 6).
마지막으로 NCLS(Normalized Cumulative Lagrangian Separation)는 다음과 같다.
식(7)과 식(8)은 Liu and Wiesberg(2011)가 표층 뜰개의 이동예측평가 방법으로 제시한 NCLS(Normalized Cumulative Lagrangian Separation)이다.
여기서, di는 관측지점과 모델의 거리차를 나타내며 loi는 관측치 이동거리의 누적합, N은 자료의 수, n은 임계치를 나타낸다. NLCS에 사용되는 임계치 n은 모델을 평가하는 영역과 수준에 따라 임의로 조절할 수 있으며, SS 값이 1에 가까울수록 모의를 완벽하게 한 것으로 판단 할 수 있다(Table 6). 본 연구에서는 참고문헌(Lee et al., 2017)에서 제시한 n = 1을 선택하여 적용하였다.
3. 결과 및 고찰
3.1 대한해협에서의 표층 뜰개 이동 경로
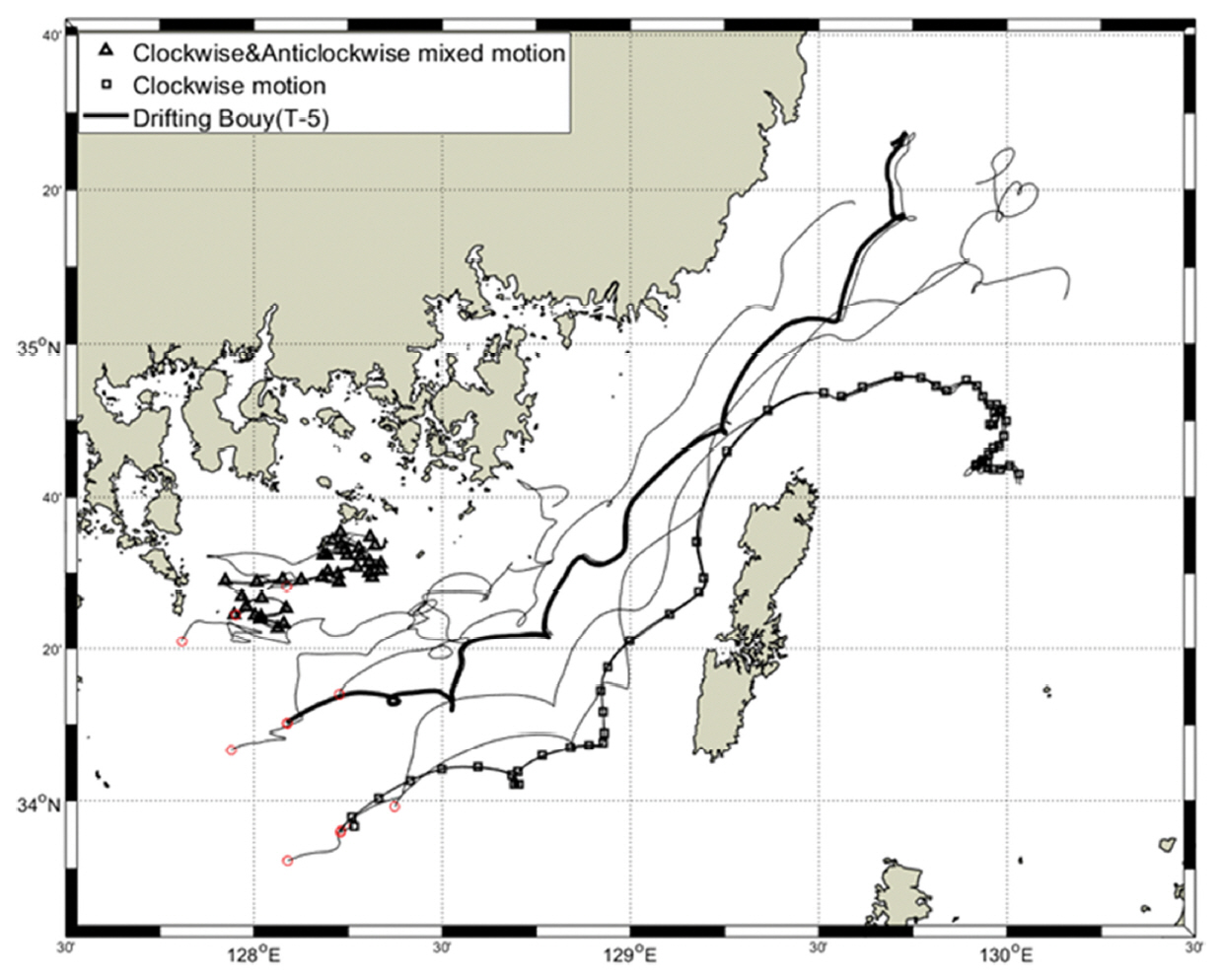
본 연구에서는 Fig. 1의 총 9개 정점(T-1~T-9)에 15개의 표층 뜰개를 투하하여 이동 경로를 관측하였다. 2020년 7월 21일부터 7월 28일까지 투하된 15개 표층 뜰개의 대한해협에서의 이동 경로 관측 결과는 Table 7 및 Fig. 2에 제시하였다.
결과적으로 Fig. 2에서 알 수 있듯이 전남 여수시 연도 전면 해역과 인접한 정점 T-1~T-3에 투하한 표층 뜰개는 시계 또는 반시계 방향의 회전 운동이 혼합되어 나타났으며, 일부는 연안에 갇혀있는 모습을 보였다. 이에 반해 정점 T-4~T-9에 투하한 표층 뜰개는 시계방향 운동을 하며 북동향으로 이동하였다. 또한 투하된 표층 뜰개 중에서 총 직선 이동거리가 가장 작은 것은 정점 T-3으로 약 20.20 km이었으며 가장 멀리 이동한 것은 정점 T-7로 약 233.31 km이었다(Table 7). 그리고 투하된 표층 뜰개의 평균 직선 이동 거리를 산정해 보면 연안과 인접한 내측에 투하된 정점 T-1~T-3의 표층 뜰개의 경우 약 38.64 km, 중앙부에 해당하는 정점 T-4~T-6의 표층 뜰개의 경우 약 175.63 km, 연안과 가장 먼 외측에 투하된 정점 T-7~T-9의 표층 뜰개의 경우 약 199.11 km를 이동하였다.
이상의 결과는 지형류 및 계절풍의 영향에 의해서 연안에 인접한 표층 수괴는 상대적으로 외해측 수괴와 다른 흐름 패턴을 가진다고 생각할 수 있다. 또한 수심이 낮은 해안 쪽에서는 해저 마찰의 영향으로 해류 성분보다는 천해 조류의 영향이 더 크게 작용하기 때문에 일어나는 현상이라고 판단된다.
3.2 표류예측 모델의 정확도 평가
본 연구는 표층뜰개 관측 결과와 해수유동 예측 수치모델 기반 표류예측모델 2종(MOHID, ROMS), 기계학습 기반 표류예측모델 2종(선형 회귀, 의사결정나무)에 대해서 예측 정확도를 평가하기 위해 상술한 3가지 오차평가방법을 적용하고 그 결과를 Table 8에 제시하였다.
표층 뜰개와 입자추적 수치예측모델 2종(MOHID, ROMS)과의 성능 평가결과를 살펴보면 표층 뜰개와 MOHID 예측 자료의 CC는 U성분 0.3021, V성분 0.2707이었으며, RMSE 는 U성분 0.4017 m/s, V성분 0.4069 m/s로 나타났다. 또한 표층 뜰개와 ROMS 예측자료의 CC는 U성분 -0.1468, V성분 0.1704이었으며, RMSE는 U성분 0.5618 m/s, V성분 0.4429 m/s로 나타났다.
표층 뜰개 관측 결과와 기계학습 2종(선형 회귀, 의사결정 나무)과의 성능 평가결과를 보면 표층 뜰개와 선형회귀 예측 자료의 CC는 U성분 0.5310, V성분 0.2379이었으며, RMSE는 U성분 0.3069 m/s, V성분 0.3669 m/s로 나타났다. 또한 표층 뜰개와 의사결정나무 예측자료의 CC는 U성분 0.9215, V성분 0.9123이었으며, RMSE는 U성분 0.1696 m/s, V성분 0.1880 m/s로 나타났다. NCLS 계산결과는 MOHID(0.8885) > 의사결정나무(0.8768) > 선형 회귀(0.7536) > ROMS(0.2168) 순으로 나타났다. 연안역에서 관측된 자료를 학습하여 이동 예측을 하는 방법은 100시간 이후 표층 뜰개의 이동경로에 활용할 수 있는 관측소 위치가 제한적인 것과 표층 뜰개 및 관측소 자료들의 시간간격(60분)의 한계로 자료수가 적었다. 이로 인해 정확도가 과적합되어 나타난 부분이 있는 것으로 사료되며, 이는 향후 연안에서 예측 정확도를 높이기 위해 표층 뜰개와 관측소의 자료수집 간격을 줄이는 방법을 통해 개선이 가능할 것으로 보인다. 그리고 기계학습에 있어 학습자료의 품질과 하이퍼파라미터 설정에 따라 정확도 차이가 나타날 수 있기 때문에 입력자료에 사용되는 관측자료의 품질개선 및 하이퍼파라미터별 실험을 통해 개선될 수 있을 것으로 판단된다.
3.3 표층 뜰개 관측자료와 표류 예측자료 결과
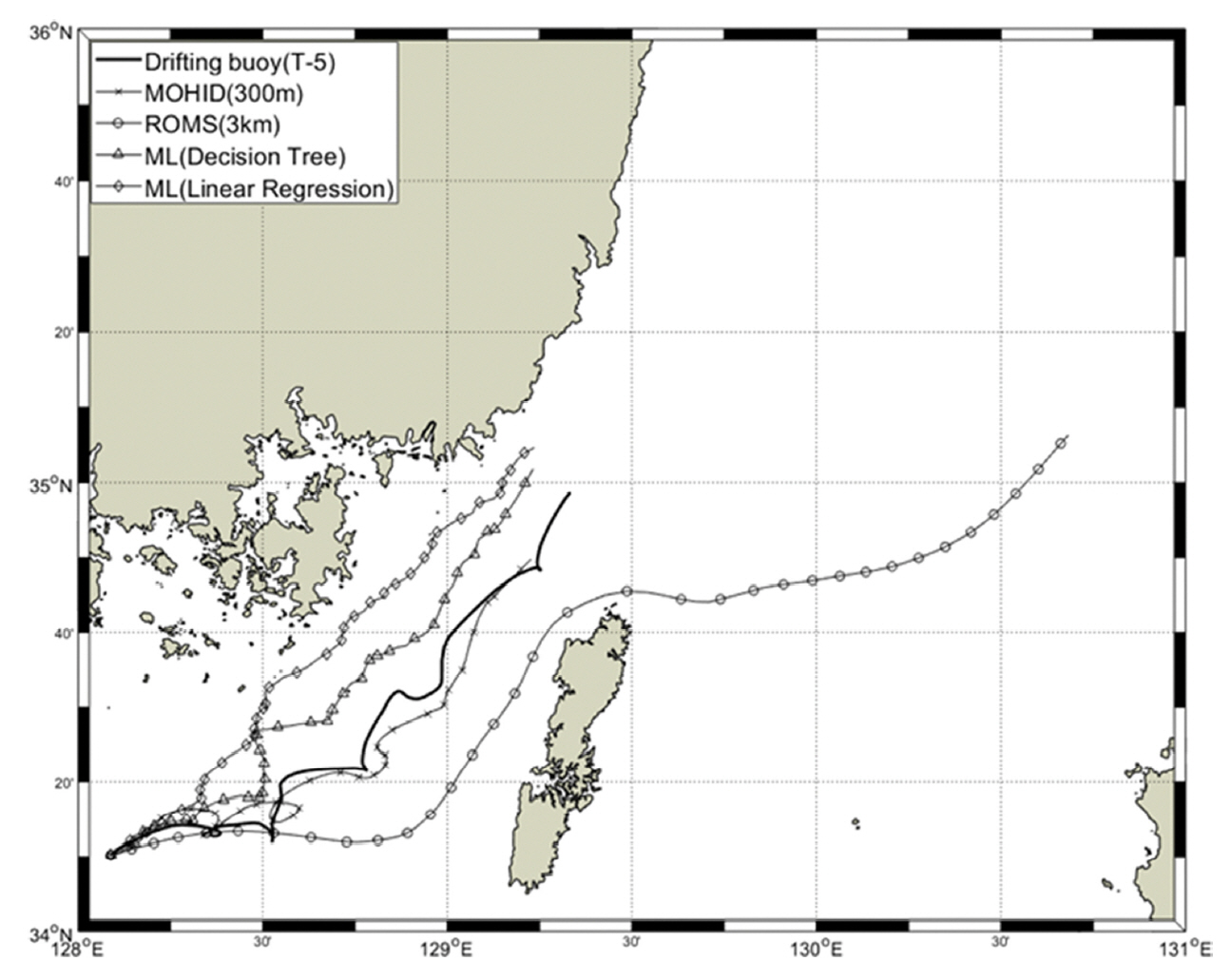
결과적으로 그림에서 표층 뜰개의 이동 경로와 가깝게 이동한 예측모델은 MOHID로 나타났으며, 의사결정나무의 전체적인 이동 경향성이 매우 유사하게 나타났다.
하지만 ROMS의 경우 다른 입자추적 모델에 비해 이동거리가 과대 모의되는 경우가 나타났는데 이는 수치모델 해상도에 의한 한계로 사료된다. Nyquist Theorem에 따르면 특정 해양현상을 관측, 모의하는데 필요한 시·공간적 해상도는 2배를 권장하고 있고, 실제로는 약 4배의 주기로 관측, 모의를 해야 한다. 본 연구에서는 수치모델의 예측기간을 1시간 단위로 했으나, MOHID의 경우 공간적인 해상도(300 m)에 비해 시간적인 해상도가 작았다. 이를 반영하여 실험할 경우 이전보다 높은 예측 정확도가 기대된다. 또한 선형회귀의 경우 이동거리로만 봤을 때는 MOHID, 의사결정나무와 큰 차이가없으나 100시간까지의 이동 경향은 유사하지 않았다. 이는 자료의 패턴을 일차식으로만 가정했기 때문인 것으로 추론된다. 따라서 이는 향후 2차 이상의 다항식 선형회귀 학습법을 이용한 추가 연구가 필요한 것으로 생각된다.
4. 결론
본 연구는 대한해협 인근 입자추적 예측 기법의 정확도 개선을 위해서 해수유동 수치모델 결과를 이용하여 만든 입자 추적 모델과 현장 관측 자료를 이용한 기계학습 기반 입자 추적 모델을 비교 및 분석하였다. 본 연구를 통해서 얻어진 요약하면 다음과 같다.
첫째, 대한해협에서 실시한 표층 뜰개 이동경로 실험에서 연안 해역과 인접한 정점에 투하한 표층 뜰개는 시계 또는 반시계 방향의 회전 운동이 혼합되어 나타났으며, 일부는 연안에 갇혀있는 모습을 보였다. 이에 반해 연안과 가장 먼 외측에 투하된 정점에 투하한 표층 뜰개는 시계방향 운동을 하며 북동향으로 이동하였다. 이는 지형류 및 계절풍의 영향에 의해서 연안에 인접한 표층 수괴는 상대적으로 외해측 수괴와 다른 흐름 패턴을 가진다고 생각할 수 있다. 또한 수심이 낮은 해안 쪽에서는 해저 마찰의 영향으로 해류 성분보다는 천해 조류의 영향이 더 크게 작용하기 때문에 일어나는 현상이 라고 판단된다.
둘째, 관측된 표층 뜰개 중 1개(정점 T-5) 자료와 수치모델 예측자료(ROMS, MOHID), 가거도, 거제도, 교본초 조위관측소의 조위, 바람자료를 학습시켜 만든 기계학습(선형 회귀, 의사결정나무) 기반 예측자료를 이용하여 3가지 오차평가방법 (상관계수, 평균제곱근오차, NCLS)을 적용하여 비교하였다. 그 결과로서 CC와 RMSE에서는 의사결정나무 모델의 예측 정확도가 가장 우수하였고 NCLS에서는 MOHID 모델이 예측 결과가 가장 우수하였다.