Long-gap Filling Method for the Coastal Monitoring Data

Hong-Yeon Cho; Gi-Seop Lee; Uk-Jae Lee

doi:10.9765/KSCOE.2021.33.6.333

Journal of Korean Society of Coastal and Ocean Engineers > Volume 33(6); 2021 > Article

해양모니터링 자료의 장기결측 보충 기법

Article

J Korean Soc Coast Ocean Eng 2021; 33(6): 333-344.

Published online: December 31, 2021

DOI: https://doi.org/10.9765/KSCOE.2021.33.6.333

해양모니터링 자료의 장기결측 보충 기법

조홍연^*, 이기섭^**, 이욱재^***

^*한국해양과학기술원 해양빅데이터센터 책임연구원, UST 교수

^**한국해양과학기술원 해양빅데이터센터 UST 학생연구원(박사과정)

^***한국해양과학기술원 해양빅데이터센터 연수생

Long-gap Filling Method for the Coastal Monitoring Data

Hong-Yeon Cho^*, Gi-Seop Lee^**, Uk-Jae Lee^***

^*Principal Research Scientist, Marine Big-data Center, Korea Institute of Ocean Science and Technology; Professor, University of Science and Technology, Haeyangro 385, Youngdo, Busan 49111, Korea

^**Student Researcher, Marine Big-data Center, Korea Institute of Ocean Science and Technology

^***Student Apprentice, Marine Big-data Center, Korea Institute of Ocean Science and Technology

Corresponding author: Hong-Yeon Cho, Principal Research Scientist, Marine Big-data Center, Korea Institute of Ocean Science and Technology; Professor, University of Science and Technology, Haeyangro 385, Youngdo, Busan 49111, Korea, Tel: +82-51-664-3786, hycho@kiost.ac.kr

Received November 15, 2021 Revised December 3, 2021 Accepted December 20, 2021

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted noncommercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

요약

해양모니터링 자료에서 빈번하게 발생하는 장기결측구간의 자료 보충기법을 제안한다. 제안하는 방법은 결측구간의 장기변동 추세 성분과 단기변동 잔차성분을 추정하여 조합하는 방식으로 결측구간의 미지 정보를 추정한다. 이 방법을 이용하여 울릉도 해상부이 자료의 수온 항목, 약 1개월 정도의 장기결측 구간의 자료를 보충하였으며, 부이에서 관측하는 자료 항목에 대해서도 결측 보충을 수행하였다. 보충된 자료는 항목에 따라 차이를 보이지만 변동양상이 적절하게 재현되는 것으로 파악되었다. 이 방법은 추세추정과 잔차 반영에 따른 편향오차와 분산오차가 발생하지만, 장기결측으로 인한 통계적인 측도 추정의 편향오차는 크게 절감하는 것으로 파악되었다. 결측보충 모형의 추정 RMS 오차의 평균과 90% 신뢰구간은 각각 0.93, 0.35~1.95 범위이다.

핵심용어: 해양모니터링 자료, 결측자료 보충, 장기추세, 단기 변동잔차, 울릉도 부이

Abstract

Technique for the long-gap filling that occur frequently in ocean monitoring data is developed. The method estimates the unknown values of the long-gap by the summation of the estimated trend and selected residual components of the given missing intervals. The method was used to impute the data of the long-term missing interval of about 1 month, such as temperature and water temperature of the Ulleungdo ocean buoy data. The imputed data showed differences depending on the monitoring parameters, but it was found that the variation pattern was appropriately reproduced. Although this method causes bias and variance errors due to trend and residual components estimation, it was found that the bias error of statistical measure estimation due to long-term missing is greatly reduced. The mean, and the 90% confidence intervals of the gap-filling model’s RMS errors are 0.93 and 0.35~1.95, respectively.

Keywords: coastal monitoring data, gap-filling, trend, residuals, Ulleungdo buoy

1. 서론

해양환경 모니터링은 고립되고 열악한 환경에서 관측이 수행되고 있기 때문에, 어떤 예상할 수 없는 또는 극한적인 환경의 영향으로 관측장비가 작동이 중지되거나 오작동되는 경우가 빈번하게 발생한다. 또한 이러한 상황이 인지되었다 할지라도 신속한 복구 대응이 곤란하고 복구에 긴 시간과 비용이 소요되기 때문에 장기결측 발생이 불가피하다. 일시적인 환경조건에서 이상이 발생하였다가 바로 자동 복구되는 단기 결측 자료는 연속적으로 관측되는 다량의 자료에서 차지하는 비중이 크기 않기 때문에 기본적인 내삽 추정 정도로도 결측을 채우고 다양한 통계적인 분석을 수행하여도 무방하다. 그러나 관측장비의 복구로만 관측이 재개되는 경우에는 해양모니터링의 경우 장기간의 결측발생이 불가피하며, 결측구간이 포함되어있는 자료(incomplete data)를 이용하는 경우 전체적인 해양환경 변화의 통계적인 추정·분석을 저해한다. 센서를 이용하는 현장관측 자료는 Time-Series(TS) 자료이기 때문에 결측이 발생하면 실질적으로 그 자료의 복구·재생이 불가능하고, 그 결측구간을 포함하여 자료의 다양한 통계적인 추정을 수행하는 경우, 편향(bias)이 크게 발생하고, 다양한 통계 측도 추정의 신뢰수준을 크게 저하시키고, 추정 결과로 인한 자료의 변동 구조 해석에 오류를 유발할 수 있다. 결측이 없는 완전한 모니터링 자료(complete data)가 장기간 구축되어 있는 경우에는 결측이 있는 해당 연도의 자료를 모두 제외하고 분석할 수 도 있다. 그러나 일반적으로 현장 관측자료는 단기간으로 제한되어 있거나, 장기간이라 할지라도 어느 정도의 결측은 포함하고 있는 경우가 대부분이다. 따라서 결측 구간의 크기와 자료의 변동특성을 반영하는 적절하고 실용적인 결측구간의 자료 보충이 요구된다. 결측자료 보충기법은 다양한 분야, 다양한 항목, 다양한 조건, 다양한 유형의 방법이 개발·적용되고 있다(Golyandina and Korobeynikov, 2014; Kang et al., 2019; Hair Jr. et al., 2010; Sim et al., 2015). 보다 구체적인 결측 보충 연구는 다양한 분야에서 특정 항목에 국한되어 수행되어 왔다. 표층 해류자료(Fredj et al., 2016), Climate Change Initiative(CCI) 토양습윤 자료(Almendra-Martin, 2021), 해양센서자료의 Real-Time 보충(Velasco-Gallego and Lazakis, 2020), 강우 자료(Sattari et al., 2020; Bellido-Jimenez et al., 2021), 위성 정보를 이용한 LAI(leaf area index) 산출정보(Kandasamy et al., 2013), 수량자료 (Baddoo et al., 2021), Eddy Covariance Carbon 플럭스 자료(Zhao and Huang, 2015), 다양한 기후(기온, 습도, 바람 항목) Time-Series 자료(Afrifa-Yamoah et al., 2020), PM10 농도자료(Rumaling et al., 2020), SAR(Search and Rescue) 자료(Wang et al., 2021), VIIRS/NOAA-20 해색산출 정보 (Liu and Wang, 2019), 지표온도 및 NDVI 자료(Sarafanov et al., 2020), 연안해역의 수온 자료(Cho et al., 2013) 등의 결측정보 추정에 다양한 방법을 개발·적용하고 있다. 그러나 대부분의 경우, 특정한 항목, 특정한 자료조건에서 적용하는 특화된 추정이기 때문에 예측성능은 우수하다고 할지라도 다른 영역에서의 적용에는 큰 제한이 따른다. 따라서 최소한의 조건에서도 장기간의 결측정보 추정이 가능한 굳건한(robust) 기법 개발이 필요하다.

결측구간의 자료보충은 보충하고자 하는 자료 항목을 허용 가능한 정도로 제한할 수 있는 수치모형이 가용한 경우에는 모델을 이용하여 해당 기간, 지점의 항목을 보충하는 방법이 이론적으로 타당한 방법이다. 그러나 수치모형도 어느 정도의 재현한계 및 해상도의 한계, 모형 수행을 위한 입력자료의 불확실성 등의 영향으로 그 활용에 한계가 따른다. 따라서, 본 연구에서는 결측구간 자료 보충을 위한 가용 자원이 지금까지의 관측자료로 제한되는 최악의 조건에서, 그러나 일반적인 상황에서 적용할 수 있는 새로운 장기간의 결측구간 자료 보충 기법을 제안하고, 그 기법의 성능평가를 목적으로 한다. 이 방법은 결측 보충 대상 항목의 자료만을 사용하기 때문에 결측이 발생하는 다양한 여건에 적용가능한 방법이며, 결측보충을 장기적인 관점의 smoothing 성분추정과 관측자료에서 분리한 잔차(residuals)를 이용하여 단기변동 성분(shortterm)의 특성을 유지하는 추정을 구분하여 수행한다는 측면에서, 본 연구에서 제안하는 새로운 기법이다.

2. 재료 및 방법

2.1 해양모니터링 자료

본 연구는 기상청(KMA) 울릉도 해양부이(131.1144 E, 37.4554 N) 자료를 대상으로 이용하여 수행하였다. KMA 해상부이에서는 2011년 11월 28일부터 1시간 간격으로 자료를 생산하고 있으며, 2020년 12월 31일까지의 자료를 이용하였다. 관측항목은 풍속, 풍향, 순간풍속(gust wind-speed), 기압, (상대)습도, 기온, 수온, 최대파고, 유의파고, 평균파고, 평균 주기, 파향 등의 총 12개 항목이다. 풍속과 순간풍속, 최대파고, 유의파고, 평균파고는 상관관계가 매우 높은 관측 항목이다. 이 부이자료의 최대 결측구간은 관측항목에 따라 약간 차이를 보이고 있으나, 2013년 4월 7일~5월 9일(약 780시간) 기간으로, 대략 1개월 정도의 장기결측으로 간주된다.

2.2 장기결측구간의 자료보충 기법

장기결측과 단기결측에 대한 개념적인 구분이 필요하다. 명확한 정량적인 정의가 있는 것은 아니지만, 실용적인 측면에서 본 연구에서는 장기결측과 단기결측을 다음과 같이 정의한다. 단기 결측은 전체자료(또는 일반적인 특성기간 = 1년)에서 하나의 연속적인 결측구간이 차지하는 비율이 10% 이하(Hair Jr. et al., 2010), 또는 관측간격을 기준으로 하는 경우, 관측간격의 10배 이하 정도로 무작위하게 발생하는 결측으로 정의한다. 반면, 장기결측은 관측장비(센서) 기준으로 시간 상관거리(temporal correlation length) 규모의 정도(order) 를 크게 넘어서는 크기로, 대략 100~1,000배 정도로 정의한다. 이 정의를 적용하는 경우, 본 연구에서 사용하는 해상부이 자료의 경우, 관측 간격이 1시간이고, 결측구간이 780시간 정도이기 때문에 장기결측으로 간주할 수 있으며, 대략 100시간(약 4일) 정도 이상되는 결측구간은 장기결측으로 간주한다. 장기결측과 단기결측의 정량적인 기준은 관측항목과 변화 양상에 따라 다른 적절한 기준을 수립할 필요가 있을 것으로 판단한다. 절대적인 기준으로는 파악하고자 하는 변화 양상의 기간규모 수준을 기준으로 할 수 있다. 예를 들면, 계절변화를 파악하고자하는 경우, 한달 정도 또는 그에 버금가는 시간규모가 기준이 될 수 있다.

이런 기준에 근거하여 장기결측이 존재하는 경우, 본 연구에서는 다음과 같은 새로운 결측보충 기법을 제안한다. 이 기법은 다음과 같은 개념적인 작업 단계로 구성된다.

제1단계: 장기간의 결측구간 시간규모를 기준으로 결측이 있는 관측자료를 long-term(추세성분 또는 장기적인 변동 성분), short-term(잔차성분 또는 단기변동 성분)으로 관측자료를 성분 분리하는 단계,

제2단계: 장기 결측구간의 변동양상을 long-term 성분의 변동양상 관점에서 추정하는 단계, 제3단계: 그리고 결측구간의 long-term 추정성분과 추정성분의 조건과 통계적으로 유사한 잔차성분(short-term, fluctuation, residuals)을 추출하여 결측 구간의 자료를 보충하는 단계로 구성된다.

자료의 구성단계에서 발생할 수 있는 불연속적인 변동 특성은 가용한 단기간의 결측보충 기법으로 채우는 것이 가능하다. 본 연구에서는 기상청 울릉도 해양부이 자료(최대 연속 결측기간 780시간, 약 1개월)를 이용하여 수행하였으며, 통계적으로 어느 정도 그럴듯한(more likely, not most likely) 변동 양상을 재한하는 것으로 파악되었다. 그러나 이 방법은 결측 기간동안에 평상적인 조건과는 다른 이벤트 영향을 고려할 수 없기 때문에 결측기간 동안에 이벤트가 발생한 경우에는 적용에 제한이 따른다.

보다 구체적이고 세분화된 계산과정은 다음과 같다. 전체 자료처리 및 결측구간 자료보충 추정 작업은 R 프로그램을 이용 하여 수행하였으며, 관측 자료에 포함되는 관측시간 정보는 R ‘lubridate’ 패키지(Grolemund and Wickham, 2011)를 이용하여 처리하였으며, 이상자료 진단은 ‘EnvStats’ 패키지(Millard, 2013)를 이용하였다. 결측보충 단계에서 사용한 구체적인 함수는 세부 단계에서 설명과 개념을 포함하여 기술하였다.

Step-1: 결측이 포함되어 있는 time-series data 입력(시간정 보와 항목 관측정보로 구성.) + 기본 정보(관측 간격)(자료의 입력 단계, 결측보충이 필요한 자료 입력)

Step-2: 입력 TS 자료의 관측간격 평가 및 complete data 크기의 자료 변수 구성. 관측 항목의 물리적이고 실질적인 범위를 벗어나는 자료를 진단(상한, 하한 경계를 항목에 따라 지정)하는 range-test 기법을 이용하여 명백한 이상자료는 제거하고, 결측구간으로 처리한다. 참고로 완전한 자료(complete data)라는 단어는 관측 시점-종점, 관측 간격 기준으로 결측이 없는 경우, 구성되어야 하는 개수를 가진 자료를 의미한다. 이 단계에서 구성되는 자료는 시간자료는 완전하지만, 관측항목의 결측이 포함된 incomplete 자료이다. 결측 자료 구간은 특정한 기호(NA)로 표시-처리한다(시간자료는 “lubridate” 패키지의 “ymd_hms()” 함수를 이용하여 처리).

Step-3: Incomplete data 관측항목에 대하여 결측구간(gap) 정보를 추출한다. 결측정보는 전체 기간에서 모든 결측시점, 결측종점의 정보와 연속되는 결측구간의 크기 정보를 포함한다. 이 단계에서는 “imputeTS” 패키지(Moritz and BartzBeielstein, 2017)에서 지원하는 함수를 사용하고, 추가적으로 필요한 결측구간의 크기 정보는 별도로 코딩하여 추출한다. 이 과정은 입력한 자료의 결측구간 기본정보를 추출하는 단계로, 장기 결측보충이 필요한 자료 여부인지를 판단하는 단계이다.

Step-4: 자료의 관측간격(Δt)을 기준으로 결측구간을 양분(short-gap, long-gap)한다. 양분된 결측구간에서 단기결측은 ARIMA-based Kalman smoothing 기법(na_kalman() 함수 ‘imputeTS’ 패키지, Moritz and Bartz-Beielstein, 2017)을 이용하여 우선 추정한다.

Step-5: 남은 장기결측 구간의 추정은 시간 순서대로 추정한다. 그 추정과정은 다음과 같다. 추정대상이 되는 장기 결측구간 규모의 조금 작은 규모의 smoothing curve 추정을 수행하여 장기 결측구간의 평균적인 시간 변동을 반영하는 수치를 추정한다. 이 추정은 R ‘KernSmooth’ 패키지에서 제공하는 locpoly() 함수(Wand, 2021; Wand and Jones, 1995)를 이용하여 수행하였으며, 핵심적인 매개변수에 해당하는 bandwidth 입력정보는 결측구간의 크기 정도를 사용하였다. 이 단계는 과측자료의 smoothing 성분을 bandwidth 규모의 영역에서 다항함수로 추정하는 과정이다.

Step-6: Step-5 단계에서 추정한 smoothing curve 대비 추정되는 일정 간격(추정하고자 하는 장기 결측구간의 크기 또는 그 이하)의 잔차 정보(분산)와 관측항목의 평균(+평균 경사) 정보를 추정하고 그 변수의 상관관계를 도출한다. 이 단계는 선택(option) 단계로 잔차의 통계적인 측도와 평균과 상관관계를 가지는 경우, 이 상관관계를 이용하여 단기 변동 성분을 추정하는 방법으로, 평균성분과 잔차성분의 통계적인 상관관계 정보를 이용한다는 관점에서 자료기반 추정으로 간주할 수 있다.

Step-7: 장기 결측구간의 평균 정보에 가장 근접한 잔차의 분산 구간 자료를 추출하여 장기결측구간의 smoothig curve 수치정보에 추가한다. 결측구간의 변동양상을 반영하기 위하여 추가되는 잔차 변동자료는 인접한 구간의 자료, 동일 시점의 자료 등 다양한 선택이 가능하다. 기본적인 개념은 평균과 더불어 실질적인 변동양상을 결측구간에 추가하여 보다 그럴듯한(more likely) 추정 성능을 도모하는 것이다.

Step-8: 결측구간의 시작구간, 종료구간의 자료 연결부분의 급격한 변동 구간으로 일정구간(대략 단기결측구간의 평균 또는 최대크기 정도로 설정)을 지정하여 결측자료로 대체하고, 그 결측구간은 단기결측구간으로 step-4 단계의 기법을 이용하여 결측구간을 추정한다. 이 구간의 결측 보충은 na_kalman() 함수를 이용하였으며, 전체 결측구간에서 일부 구간을 차지하고 있으나, 결측이 시작되고, 종료되는 지점에서 자연스러운 연결을 수행하는 단계이다. 단기간의 결측 보충이지만, 통계적으로 또는 ARIMA 기반 시계열 모형을 이용한 단기 예측 단계에 해당한다.

Step-9: 이러한 장기결측구간 추정과정을 모든 장기결측 구간에 대하여 시간 순서대로 반복한다. 반복이 완료되면, 결측보충이 완료된 자료의 결측여부 검토를 점검하고, 결측이 없는 경우, 보충을 종료한다. 결측보충을 가장 큰 구간부터 단계적으로 수행하면, 장기 결측구간의 자료보충이 모두 완료되고, complete 자료 세트가 구성된다.

Step-10: 결측자료 보충 전·후의 기본 통계정보를 추정-제시 한다. 이 자료는 자료의 결측보충여부에 따른 통계정보 변화 정도로 결측추정의 정량적인 영향 파악을 위한 참고자료로 사용한다(이 단계도 option, 결측구간의 자료보충을 그림으로 제시하는 경우, 자료의 변동양상이 어느 정도 반영 되었는지를 시각적으로/개략적으로 판단하는 단계이다).

2.3 제안된 장기결측자료 보충 모형의 오차평가

본 연구에서 제안한 장기 결측자료보충 모형(long-gap filling model, LGF model)은 다음과 같은 과정을 거쳐 RMS(root mean squared) 오차 기반 성능평가를 수행하였다. 오차기반 성능평가 과정은 결측이 없는 자료를 이용하여, 가상의 결측 구간을 생성하고, 그 구간을 추정하여 오차를 비교한다.

Step-1: [준비단계] “complete” 자료 준비: 결측이 없는 완전한 자료를 준비한다. 본 연구의 경우, 본 연구에서 제안한 기법을 이용하여 결측을 모두 보완한 울릉도 부이(수온) 자료를 사용한다. 다른 항목으로 대체하여 수행도 가능하다 (다른 “complete data” 입력하면 가능.)

Step-2: [검증단계] (세부 제1단계): 임의로 결측구간을 생성 (R 프로그램 sample.int() 함수를 사용하여 결측구간의 시점-종점 index – random 추출)하고, 생성된 구간의 자료를 비운(NA 처리, Not Available), 결측이 있는 자료를 구성한다. 생성된 결측구간의 자료는 결측자료 보충 기법의 검증을 위하여 별도 변수로 저장한다. 결측구간의 크기는 본 연구에서의 수행한 자료의 최대 결측구간 크기이다. (세부 제2단계): 본 연구에서 제안한 기법을 적용하여 결측구간의 자료를 보충한다. (세부 제3단계): 보충된 자료와 검증을 위하여 별도로 저장한 자료를 비교하여 오차(root mean squared error)를 계산한다. (세부 제4단계): 검증단계(제1단계-제3단계)를 다수(본 연구의 경우, 1,000번) 시행한다.

Step-3: [오차분석, 평가단계] 검증단계(Step-2)에서 계산된 다수의 오차자료를 이용하여, 오차의 통계정보(평균, 상한, 하한 정도 + 그림)를 계산한다.

본 연구에서 제안된 기법의 오차는 편향오차(bias), 분산오차(variance)로 구분할 수 있으나, 모형 성능평가를 위한 이 오차는 전체 추정 RMS 오차에 해당한다.

3. 결과 및 토의

3.1 관측자료의 결측 양상 및 규모

본 연구에서 제안한 장기결측구간의 자료보충 기법은 모든 항목에 적용하여 수행하였으며, 결측구간의 자료 추정 성능 분석 등은 수온 항목에 중점을 두고 수행한다. 울릉도 해상 부이 수온 관측자료의 Time-Series 도시와 결측 정보는 다음과 같다(Figs. 1~2 참고). 결측정보는 항목에 따라 차이를 보이고 있으나, 장기결측 구간은 관측장비의 전체적인 결함으로 발생하기 때문에 대부분의 항목이 전반적으로 동일하다. 단기간의 결측자료는 R ‘imputeTS’ 패키지 등을 이용하여 보충할 수 있으며, 장기결측자료 보충과정에서 발생하는 연결 구간(결측이 시작되거나 끝나는 부분으로 보충자료와 관측자료의 불연속적인 현상이 발생) 처리 등에 부분적으로 이용가능하다. 본 연구에서는 단기 결측구간 보충에 대한 내용은 생략한다.

수온 자료의 전체 개수는 79,008개이며, 결측구간의 자료 개수는 1,617개로 전체자료에서 차지하는 비율은 2.0% 정도이다. 이 비율은 전체적으로는 매우 작은 수치이지만, 2013 년 4월 7일~5월 9일(약 780시간) 기간에 780개가 집중되어 장기 결측구간을 형성하고 있음을 알 수 있다. 더불어 24시간, 91시간, 1~8시간 정도의 단기 결측도 매우 빈번하게 발생하고 있음을 알 수 있다.

수온 자료의 한 달 정도의 장기결측은 결측구간의 위치에 따라 다르지만, 동계나 하계의 고온, 저온 영역에 위치하는 경우, 평균 수온을 추정하는 과정에서 과소추정, 과대추정 등의 편향이 발생하기 때문에 정확한 추정보다는 적절한 수준에서의 추정으로 상당한 정도의 편항 저감이 가능하다. 결측구간의 자료 보충은 편향저감(bias reduction, un-biased) 목적이 가장 중요한 목적이며, 결측구간의 정확한 추정은 물리적인, 이론적인 방정식을 기반으로 하는 수치모형을 이용하여 추정하는 방법이 요구된다.

3.2 수온 자료 결측구간의 자료 보충

자료보충은 세부적인 다수의 단계로 구성되며, 대표적인 첫번째 단계는 결측구간의 장기적인 추세 추정 단계이다. 이 추세 추정은 결측구간 정도의 시간규모에서 전반적인 추세를 기반으로 결측구간의 추세성분을 추정한다. 이 과정은 자료의 평활(smoothing) 매개변수를 기반으로하는 추정이다. 자료의 평활기반 추정은 자료의 변동 상관정도가 높기 때문에 기법 측면에서는 내삽(interpolation) 문제로 변환된다고도 할 수 있다. 수온 자료의 결측구간 추세추정 결과는 다음과 같다(Fig. 3). 상단그림은 평활 매개변수(smoothing parameter) = (결측 구간의 크기), 하단 그림은 평활 매개변수 = (결측구간의 크기)/4 조건을 부여한 경우로, 상단의 경우, 과도한 평활로 판단되며, DPI 기법으로 추정한 최적 평활 매개변수 111.2 보다 매우 큰 수치로 판단된다. 하단 그림의 경우, 전반적인 변동양상을 적절한 수준으로 반영하고 있는 것으로 판단된다. 더불어 결측구간의 추세 추정도 “보다 그럴듯한(more likely)” 수준으로 판단된다.

전체 자료의 추세성분을 추정하는 경우, 잔차는 관측자료에서 추세성분을 제거한 성분으로 간단하게 계산된다. 추세 성분 추정만으로도 편향성분은 제거되지만, 실질적으로 단기 변동성분이 사라지기 때문에 추정 구간에서의 분산성분은 감소하는 비현실적인 추정으로 귀결된다. 보다 실질적인 결측 구간 자료 추정을 위해서는 적절한 잔차 성분(잔차의 분산 = 0.36)을 반영하는 과정이 필요하다. 이 변동성분은 가용한 자료구간에서 선정하여야 하며, 간단한 방법으로는 결측구간 전 ·후의 잔차성분을 이용하는 것이다. 보다 적절한 방법으로는 잔차의 평균, 분산 관계로부터 추정한 추세 성분의 평균에 부합되는 분산 크기를 가지는 잔차성분을 선택하는 방법도 있다.

본 연구에서는 가장 간단한 방법으로 결측구간 전·후의 잔차크기에 해당하는 구간 자료를 이용하여 추정하는 방법을 선택하였다. 그러나 평균과 분산의 변화 양상이 뚜렷한 경우에는 추세성분의 평균에 대응되는 분산을 가지는 잔차성분을 선택하는 방법이 오차 저감 효과가 클 것으로 판단된다. 참고로 수온 자료의 경우, 평활 매개변수 크기조건에서 계산한 평균과 분산 자료의 관계는 다음과 같다(Fig. 4 참조). 그림에서 볼 수 있는 바와 같이 수온자료의 분산은 저온, 고온 영역에서 평균보다 크게 나타나고 있음을 알 수 있다.

추세성분을 추정하고, 그 구간크기에 해당하는 잔차성분을 선택하여 추가로 반영하면, 즉 추세 성분과 잔차성분을 더하여 결측구간의 최종 추정으로 제시한다. 그 결과는 다음과 같다(Fig. 5). 그림에서 볼 수 있는 바와 같이 추세 성분에 잔차성분을 추가하는 경우, 보다 실질적인 변동 양상이 재현되는 것을 알 수 있으며, 보다 적절한 잔차성분 반영에 관한 연구는 자료 특성을 반영하여 통계적으로 가장 그럴듯한(most likely) 성분을 선택하는 기준 제시에 초점을 맞출 필요가 있다. 인접한 지점에 가용한 자료가 존재하는 경우, 높은 수준의 추정 수준을 가지는 수치모형의 지원이 가능한 경우에는 본 연구에서 제시하는 방법을 보조적으로 사용할 수 있다. 본연구의 한계는 장기 결측구간의 그 시간구간에서 발생하는 어떤 특별한 사상(event), 사건의 영향을 고려할 수 없다는 점으로, 과거의 평균적인 자료 변동양상을 반영하는 편향 제거 기법 측면에서 가치를 가진다고 할 수 있다.

3.3 수온 자료의 결측보충 추정 오차

울릉도 부이 수온 관측자료를 본 연구에서 제안한 기법을 이용하여 완전한 자료를 구성하였다. 이 “complete” 자료를 이용하여 2.3절에서 제시한 과정으로 RMS 오차정보를 추정하였다. 추정한 RMS 오차자료는 모두 1,000개이며, 평균은 0.93(C), 5~95% 하한, 상한 오차는 각각 0.35, 1.95(C)로 파악되었다(Fig. 6 참조). 간혹 발생하는 큰 RMS 오차는 하계 고온 영역의 ‘smoothing’ 성분의 부정확한 추정으로 발생하는 한계로, 이 한계는 자료의 평균적인 변화 양상만을 반영하는 본 모형의 한계이기도 하다. 이 영역의 오차는 결측 구간에서 발생하는 어떤 특정 사상(event)의 영향으로, 이 구간의 자료는 수치모형을 이용하거나 인접한 지점의 유사 항목 자료를 이용하여 추정하는 것이 바람직하다.

3.4 울릉도 부이 모든 관측항목의 결측 보충

본 연구에서 제안하는 장기 결측 구간의 자료를 추정하는 방법은 어떤 항목의 자료를 추정하는가와 어떤 변환 과정을 거쳐서 추정하는 가에 따라 상당한 정도의 정성적인 성능차이를 보이고 있음을 알 수 있다. 아래 그림은 울릉도 해상부이에서 관측하는 다른 항목에 대하여 장기 결측구간의 자료를 추정한 결과이다(Fig. 7). 그림에서 볼 수 있는 바와 같이 정성적으로 적절한 수준의 추정과 다소 부적절한 수준의 추정으로 항목에 따라 차이를 보이고 있다. 보다 적절한 추정을 위해서는 추정항목의 특성을 반영하는 자료의 변환도 상당한 영향을 미치는 것으로 파악되었다. 바람, 유속과 같은 벡터 자료의 경우, 크기와 방향자료보다는 동서방향, 남북방향의 유사한 특성을 가지는 두 성분으로 변환하여 각각 추정하는 것이 보다 개선된 결과를 보이는 것으로 검토되었으며, 파고 자료의 경우에는 적절한 변환(root-transformation) 또는 대수변환 등이 요구되는 것으로 파악되었다. 더불어 구간추정에서 국지적으로 보여지는 이상자료의 제거도 결측구간 자료추정에 영향을 미칠 것으로 판단된다.

4. 결론 및 제언

해양 모니터링 자료의 경우, 장기 결측구간이 발생한 시점으로 가용한 자료나 모델, 공식 등의 가용한 추정자원 조건 등이 다르기 때문에 매우 다양한 추정 상황이 존재한다. 가장 최적의 추정 방법은 자료보충이 필요한 지점과 시기를 기준으로 가용한 보조자료의 유무, 결측 구간의 크기와 빈도, 결측 추정 자료의 결측구간 규모의 변동양상 등을 고려하여 추정하는 선택 가능한 또는 가용한 수치모형 등의 성능을 고려하여 선택하는 과정이 필요하다. 그러나 본 연구에서는 최악의 상황, 최소한의 자원 조건에서 추정에 사용할 수 있는, 즉 가용한 자료는 현재 결측이 발생하는 또는 발생한 항목의 과거 또는 그 이후의 자료만이 가용한 상황에서 적용가능한 방법을 제시하였다. 이 방법의 기본 목표는 통계적인 편향 (statistical bias) 제거 목적의 추정으로, 추세성분과 잔차성분의 조합으로 결측구간을 추정하는 방법이다. 이 방법은 일반적인 해상 모니터링 자료 형태를 대표하는 울릉도 해상부이 자료에 적용한 결과, 수온 자료를 포함하여 다양한 관측 항목에 적용한 결과, 추가적인 정보가 없는(대부분의) 경우에도 적용 가능한 방법으로 파악되었다. 한편, 본 연구에서 세세한 검토내용은 생략하였으나, 작은 구간의 결측자료 추정은 Kalman-filter 적용방법을 추천한다.

본 연구에서 제안하는 추정 방법은 이론적인 역학(mechanics) 또는 에너지나 물질 보전 개념을 도입하여 추정한 자료가 아니고, 통계적인 개념으로 추정한 자료이기 때문에 결측구간 추정정보를 이용하여 어떤 물리적인 해석을 수행하는 것은 한계가 있다. 다만, 통계적인 분석을 위한 다양한 또는 고급 도구의 사용을 가능하도록 자료를 구성하는 것이 장기결측구간 자료보충(filling-in)의 목적이며, 통계적인 편향(bias) 제거라는 중요한 목적도 포함된다. 결측구간의 물리적인 해석을 위해서는 해당 항목의 변화양상을 이론적으로 추정할 수 있는 수치모형의 도움을 받아 추정하는 과정이 요구된다.

감사의 글

본 연구는 독도연구사업(PG-52262)의 지원을 받아 수행되었으며, 연구비 지원에 감사드립니다. 또한 해상 모니터링 자료를 제공해주신 기상청에 감사드립니다.

Fig. 1.

Time-series plot of the buoy monitoring data (mean = 17.4^o C).

Fig. 2.

Missing information plot. (NA = missing data).

Fig. 3.

Trend-component estimation of the water temperature data (Long-gap, missing interval is between two red vertical lines).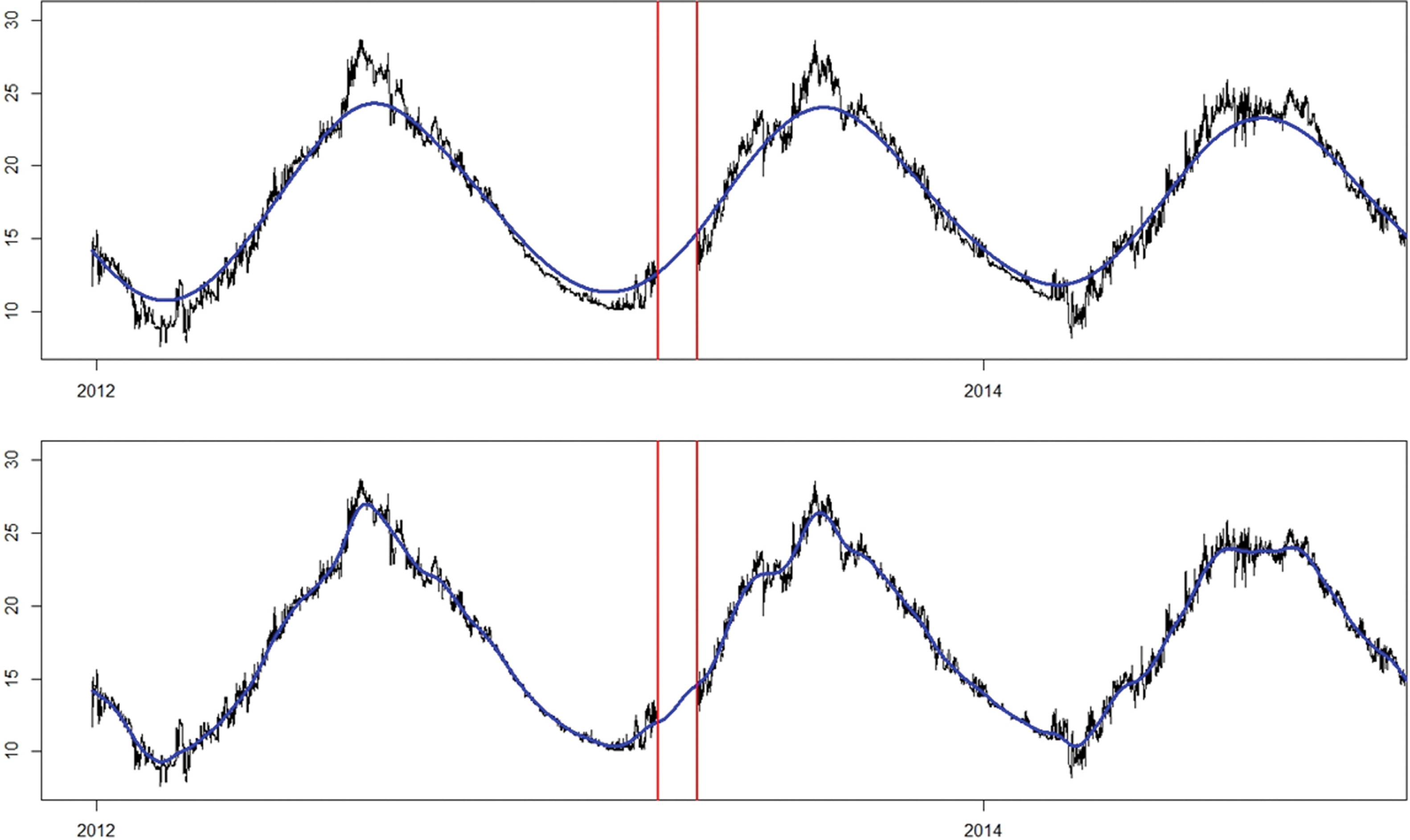

Fig. 4.

Correlation of the mean and variance of the water temperature data. (Variance of the residuals = 0.36, Mean of the variances = 0.24).

Fig. 5.

Gap-filling of the buoy monitoring data.

Fig. 6.

Histogram of the Gap-filling model RMSE.

Fig. 7.

Long-gap filling results of the diverse monitoring parameters.

References

Afrifa-Yamoah, E, Mueller, UA, Taylor, SM, Fisher, AJ. (2020). Missing data imputation of high-resolution temporal climate time series data, Meteorological Applications, https://doi.org/10.1002/met.1873.

Almendra-martin, L, Martinez-Fernandez, J, Piles, M, Gonzalez-Zamora, A. (2021). Comparison of gap-filling techniques applied to the CCI soil moisture database in Southern Europe, Remote Sensing of Environment. 258 https://doi.org/10.1016/j.rse.2021.112377.

Baddoo, TD, Li, Z, Odai, SN, Boni, K.R.C., Nooni, I.K., Andam-Akorful, S.A.. (2021). Comparison of missing data infilling mechanisms for recovering a real-world single station streamflow observation, International J. of Environmental research and Public Health. 18: https://doi.org/10.3390/ijerph18168375.

Bellido-Jimenez, J.A., Gualda, J.E., Garcia-Marin, A.P. (2021). Assessing machine learning models for gap-filling daily rainfall series in a semiarid region of Spain, Atmosphere, 12, 1158 https://doi.org/10.3390/atmos12091158.

Cho, HY, Oh, JH, Kom, KO, Shin, JS. (2013). Outlier detection and missing data filling methods for coastal water temperature data, J. of Coastal Research, (Special Issue No. 65):1898-1903.

Grolemund, G., Wickham, H. (2011). Dates and Times Made Easy with lubridate, Journal of Statistical Software, 40(3):1-25 https://www.jstatsoft.org/v40/i03/.

Hair, J.F. Jr, Black, W.C., Babin, B.J., Anderson, R.E.. (2010). Multivariate Data Analysis, A Global Perspective. Seventh Edition. Chapter 2. Pearson.

Kandasamy, S., Baret, F., Verger, A., Neveux, P., Weiss, M. (2013). A comparison of methods for smoothing and gap filling time series of remote sensing observations - application to MODIS LAI products, Biogeosciences, 10, 4055-4071 https://doi.org/10.5194/bg-10-4055-2013.

Kang, M., Ichii, K., Kim, J., Indrawati, Y.M., Park, J., Moon, M., Lim, J.-H., Chun, J.-H. (2019). New gap-filling strategies for long-period flux data gaps using a data-driven approach, Atmosphere, 10, 568 https://doi.org/10.3390/atmos10100568.

Liu, X, Wang, M. (2019). Filling the gaps of missing data in the merged VIIRS SNPP/NOAA-20 ocean color product using DINEOF method, Remote Sensing. 11 https://doi.org/10.3390/rs11020178.

Millard, SP. (2013). EnvStats: An R Package for Environmental Statistics. Springer, New York.

Moritz, S, Bartz-Beielstein, T. (2017). imputeTS: Time Series Missing Value Imputation in R, The R Journal, 9(1):207-218 https://doi.org/10.32614/RJ-2017-009.

Golyandina, N., Korobeynikov, A. (2014). Basic Singular Spectrum Analysis and Forecasting with R, Computational Statistics and Data Analysis, 71, 934-954.

Fredj, E., Roarty, H., Kohut, J., Smith, M., Glenn, S. (2016). Gap filling of the coastal ocean surface currents from HFR data: Application to the Mid-Atlantic Bight HFR Network, Journal of Atmospheric and Oceanic Technology, 33(6):1097-1111.

Rumaling, M.I., Chee, F.P., Dayou, J., Chang, J.H.W., Kong, S.S.K., Sentian, J. (2020). Missing value imputation for PM₁₀ concentration in Sabah using nearest neighbour method (NNM) and expectation-maximization (EM) algorithm, Asian Journal of Atmospheric Environment, 14(1):62-72 https://doi.org/10.5572/ajae.2020.14.1.062.

Sarafanov, M, Kazakov, E, Nikitin, NO, Kalyuzhnaya, AV. (2020). A machine learning approach for remote sensing data gap-filling with open-source implementation: An example regarding land surface temperature, surface albedo and NDVI, Remote Sensing. 12 https://doi.org/10.3390/rs12233865.

Sattari, M.T., Falsafian, K., Irvem, A., Shahav, S., Qasem, S.N. (2020). Potential of kernel and tree-based machine-learning models for estimating missing data of rainfall, Engineering Applications of Computational Fluid Mechanics, 14(1):1078-1094 https://doi.org/10.1080/19942060.2020.1803971.

Sim, J, Lee, JS, Kwon, B. (2015). Missing values and optimal selection of an imputation method and classfication algorothm to improve the accuracy of ubiquitous computing applications, Mathematical Problems in Engineering, 2015 http://dx.doi.org/10.1155/2015/538613.

Velasco-Gallego, C, Lazakis, I. (2020). Real-time data-driven missing data imputation for short-term sensor data of marine systems. A comparative study, Ocean Engineering. 218 https://doi.org/10.1016/j.oceaneng.2020.108261.

Wand, MP. (2021). KernSmooth: Functions for Kernel Smoothing Supporting Wand & Jones 1995, R package version 2.23-20. https://CRAN.R-project.org/package=KernSmooth.

Wand, MP, Jones, MC. (1995). Kernel Smoothing: Chapman and Hall, London.

Wang, G, Ma, M, Jinag, L, Chen, F, Xu, L. (2021). Multiple imputation of marine search and rescue data at multiple miss-ingpatterns, PLOS ONE. 16(6):https://doi.org/10.1371/journal.pone.0252129.

Zhao, X, Huang, Y. (2015). A comparison of the three gap filling techniques for eddy covariance net carbon fluxes in short vegetation ecosystems, 2015 http://dx.doi.org/10.1155/2015/260580.