요약경사식방파제 상치콘크리트에는 경제적인 이유와 월파의 효과적인 저감을 위해 파라펫이 설치되기도 하지만, 파라펫 설치로 인해 상치콘크리트에는 증가된 파압이 작용하게 된다. 일반적으로 상치콘크리트에 작용하는 파압은 수리실험을 통해 검토되며, 상치콘크리트 설계를 위해서는 파압이 산정되어야 하지만 여전히 불명확한 부분이 있다. 본 연구에서는 상치콘크리트에 작용하는 수평파압 산정을 위해 경사식구조물 형상과 다양한 파랑조건을 적용한 수리실험을 수행하였다. 실험결과를 이용하여 Goda(1974, 2010)의 파압산정식에 적용되는 파압저감계수를 제안하였으며, 테트라포드가 피복된 경사식방파제 상치콘크리트 설계에 실무적으로 적용 가능 할 것으로 기대된다.
AbstractThe crown wall with parapet on top of the rubble mound breakwater represents a relatively economic and efficient solution to reduce the wave overtopping discharge. However, the inclusion of parapet leads to increased wave pressure on the crown wall. The wave pressure on the crown wall is investigated by physical model test. To design the crown wall the wave loads should be available, and the horizontal wave pressure is still unclear. Regarding to the horizontal wave pressure on the crown wall, a series of experiments were conducted by changing the rubble mound type structure and the wave conditions. Based on these results, pressure modification factors of Goda’s (1974, 2010) formula have been suggested, which can be applicable for the practical design of the crown wall of the rubble-mound breakwater covered by tetrapods.
1. 서론항만구조물의 외곽시설 중 경사식구조물은 상대적으로 수심이 낮은 곳에 건설되는 것이 일반적이다. 경사식방파제 설계시 안정성 확보측면에서 항내외측 피복재 및 상치콘크리트 안정, 제체침하, 선단세굴, 제체활동 등을 검토하여야 한다. 국내 설계기준에는 항내측 피복재 안정에 대해 설계법이 확립되어 있지 않으나 현재 기초적인 연구가 이루어지고 있다. 또한 상치콘크리트 안정성에 영향을 미치는 파압산정 또한 부재하며 Goda 파압식(1974, 2010)을 이용하는 실정으로 체계적인 검토는 이루어지지 않았다. 경사식방파제 피해시 지반 측면을 제외하면, 크게 항내외측 피복재 유실과 상치콘크리트의 활동 및 전도 피해를 들 수 있다. 경사식방파제 피해발 생시 어느 항목(부분)에서부터 피해가 시작되었는지에 대한 확인이 필요하고 보완대책을 수립하는 것이 바람직하지만, 이에 대한 검토는 이루어지지 않고 있다고 판단된다. 경사식방 파제는 국내에서 가장 많이 적용되는 구조형식으로서 미흡한 설계기법에 대한 개선이 필요하다. Fig. 1은 경사식방파제 안정성 평가시 상치콘크리트의 활동 및 전도가 발생된 실험사례로서 상치콘크리트 노출부에 파력이 집중되어 피해가 발생하였다. 상치콘크리트는 국내에서 적용하고 있는 설계법에 따라 제원이 결정되었지만 피해가 발생된 사례이다.
경사식방파제 설계항목 중, 상치콘크리트 안정성 확보와 관련하여 상치콘크리트에 작용하는 수평파압에 대한 국내 연구는 미미하지만, 해외에서는 지속적으로 수행되고 있다. 대표 적인 연구로는 Pedersen(1996)의 연구를 들 수 있으며, 여러 후속 연구는 Pedersen의 연구성과를 기반으로 하고 있다. Nørgaard et al.(2013)은 Pedersen의 파압산정식이 천해조건 시와 노출부(파라펫 구간)의 파압을 과대평가함을 지적하고, Pedersen이 제안한 식을 수정하였다. 또한 Martin et al.(1999) 은 규칙파를 적용한 실험을 통해 상치콘크리트에 작용하는 파압에 대한 결과를 제시하였다. 이외에도 여러 연구자들에 의해 경사식구조물의 상치콘크리트에 작용하는 파압에 대한 연구가 수치해석 및 수리실험을 통해 수행되어 왔다(Guanche et al., 2009; Chen et al., 2015; Contestabile et al., 2017; Doorslaer et al., 2017; Jacobsen et al., 2018; Molines et al., 2018; Aniel-Quiroga et al., 2019; van Gent and van der Werf, 2019; Formentin et al., 2021). Aniel-Quiroga et al.(2019)은 고립파를 이용하여 지진해일시 상치콘크리트에 작용하는 파압에 대한 연구를 수행하였으며, van Gent and van der Werf(2019)는 경사식방파제 상치콘크리트에 작용하는 파랑의 입사각 영향을 검토하였다.
본 연구에서는 경사식방파제의 상치콘크리트에 작용하는 파압에 대한 2차원 수리실험을 수행하고 그 결과를 분석하였다. 비쇄파조건에서 불규칙파의 파고와 주기를 변경시키며 실험을 수행하였으며, 계측은 파력계를 이용하였다. 실험단면은 경사식방파제에서 피복재가 거치되지 않은 단면과 테트라포드가 거치된 단면을 대상으로 하였다. 실험결과는 Goda 파압 식에 의한 결과, Pedersen 및 Nørgaard et al.의 결과와 비교하였으며, 국내에서 상치콘크리트 설계시 적용하고 Goda 파압식의 파압보정계수를 제안하는 것을 목표한다.
2. 기존 연구2.1 국내 적용 방법경사식방파제 설계시 상치콘크리트의 안정을 확보하기 위해서는 상치콘크리트에 작용하는 수평파압을 산정하여야 한다. 국내에서는 이에 대한 파압산정법이 제시되어 있지 않아 Goda(1974, 2010) 파압산정식과 Takahashi et al.(1990)의 파압보정계수를 활용하여 산정하고 있는 실정이다. Goda 파압식에서 정수면에 작용하는 최대파압은 식(1)과 같다.
식(1)에서 β는 입사각, ρ는 유체의 밀도, g는 중력가속도, λ1과 λ2는 구조물의 형상에 따른 보정계수, α1과 α2는 각각 중복파압과 쇄파압계수, H는 파고이다. Goda 파압은 정수면에서 최대파압을 보이며, 구조물 상부로 올라갈수록 선형적으로 감소한다.
소파블록으로 충분히 피복된 단면에서 정수면에 작용하는 최대파압(p1)은 식(2)와 같다.
식(2)는 소파블록으로 충분히 피복된 경우에는 쇄파압이 현저히 감소하므로 Goda 파압산정식에서 쇄파압계수(α2)를 α2 = 0으로 하고, 구조물 형상에 따른 파압보정계수(λ1)를 λ로 대체한 것이다. Takahashi et al.(1990)은 전사면 피복 혼성제를 대상으로 소파블록 피복에 따른 파압보정계수 λ를 식 (3)과 같이 제안하였다.
그리고 식(3)에서 경사식방파제 상치콘크리트와 같이 직립벽이 정수면 부근에 있는 경우에는 입사파의 주기에 따라 파압 보정계수(λ)가 크게 변화하므로 주기가 긴 경우에는 λ = 1을 사용하도록 하고 있다.
2.2 해외 연구결과경사식방파제 상치콘크리트에 작용하는 파압 산정에 대한 체계적인 연구는 Pedersen(1996)에 의해 시작되었다고 할 수있다. Pedersen은 300 cases 이상의 많은 2차원 수리모형실 험을 수행하고 파압실험 결과와 처오름높이 등을 이용하여 상치콘크리트에 작용하는 파압산정식을 제안하였으며, 연구에 사용된 기본개념은 Fig. 2와 같다. Fig. 2에서 fC와 hprot는 각각 노출부와 보호부(피복부) 높이, RU는 처오름높이, RC 와 AC는 각각 상치콘크리트와 피복재 높이, GW는 피복재 어깨폭, V0는 처오름 속도, V1과 V2는 각각 정수면 상부 피복재와 처오름 수괴의 체적, y는 처오름수괴의 두께이다. Pedersen은 Fig. 2에 도시된 개념을 이용하여 노출부(unprotected part)와보호부(피복부, protected part)에 작용하는 파압산정식을 제안하였으며, 식(4)와 같다.
식(4)에서 L은 파장이며, pm과 V는 각각 식(5)로 산정된다.
식(5)에서 Ru, 0.1%는 0.1% 초과파에 대한 처오름높이이며, van der Meer and Stem(1992)의 연구성과를 이용하였다. 식(6)에서 ξ0는 쇄파매개변수(surf similarity parameter)로서 ξ0 =tanα/(H1/3/L)0.5이고, tanα는 경사식방파제 제체사면경사이다.
Nørgaard et al.(2013)은 Persersen(1996)의 제안식이 천해 조건과 노출부에서 파압이 과대산정됨을 지적하고, 추가적인 실험을 통해 상치콘크리트에 작용하는 파압산정식을 개선하 였다. Nørgaard et al.이 제안한 파압산정식은 식(4)와 동일하고, 식(5)의 pm 산정시 사용되는 Ru, 0.1% 산정식을 다음과 같이 개선하였다.
Persersen(1996)의 실험범위는 ξ0 = 1.1~5.2, AC/H1/3 = 0.67~ 2, RC/AC = 0.3~1.1, H1/3/d = 0.16~0.35, cotα = 1.5~3.5이며, Nørgaard et al.(2013)의 실험범위는 ξ0 = 3.31~4.64, AC/H1/3 = 0.88~1.92, RC/AC = 1~1.7, H1/3/d = 0.19~0.55이다.
3. 실험시설 및 실험조건3.1 실험시설본 실험은 전남대학교 해안항만실험센터 2차원 수로에서 수행되었으며, 사용된 단면수로의 제원은 폭 1.4 m, 길이 40 m, 높이 1.5 m이며, 전기서보피스톤식 조파기가 설치되어 있고, 규칙파 및 불규칙파를 조파할 수 있다. 수로내에서 구조물설치로 인한 반사와 조파판에서 발생하는 재반사를 효과적으로 제어하기 위해 수로가 분할(폭 0.8 m와 폭 0.6 m)되어 있으며, 분할된 폭 0.8 m에는 실험모형을 설치하여 제반 자료를 취득하고, 폭 0.6 m에서는 입사파의 설정 및 보정을 수행한다. 또한 조파판 전면에 부착된 파고계를 이용하여 독취한 자료를 바탕으로 반사파 흡수식 제어가 가능하고 수로 양쪽 끝부분에 소파시설이 설치되어 있다. 설치된 조파기의 성능은 최대 파고 0.75 m, 재현가능 주기는 0.5~7 sec이며, Fig. 3은 단면 수로의 개념도이다. 본 실험에서 자유수면계측에 활용된 파고계는 용량식 파고계로서 계측범위는 ±0.35 m, 독취율은 100 Hz이며, 파력계 독취율은 2 kHz이다.
3.2 실험파 조건실험에 적용된 실험파 및 실험수심은 Table 1에 제시되어 있다. 구조물 설치위치에서의 수심(d)은 0.5 m, 실험파의 목표 유의주기(significant wave period, (T1/3)t)는 (T1/3)t = 1.6, 2.0, 2.4, 2.8, 3.2 sec, 목표 유의파고(significant wave height, (H1/3)t)는 (H1/3)t = 0.12, 0.16, 0.20 m를 적용하였다. 실험은 축척 1/25 개념으로 계획함으로 인해 원형상 목표 유의주기는 (T1/3)t = 8, 10, 12, 14, 16 sec, 원형상 목표 유의파고는 (H1/3)t = 3, 4, 5 m이다. 그리고 실험파는 Bretschneider-Mitsuyasu 주파수 스펙트럼을 이용하여 설정하였다. 목표 유의파고와 유의주기를 대상으로 실험파를 설정하더라도 동일한 제원을 가지는 파랑을 재현하기는 어렵다. 본 실험에서 설정된 실험파 의 유의파고 및 유의주기는 목표 제원과 약간의 차이가 있지만 스펙트럼과 파랑제원을 최대한 목표값에 근사하도록 설정하였다. 실험파의 유의주기는 T1/3 = 1.62~3.39 sec, 유의파고는 H1/3 = 0.126~0.243 m 범위로 설정되었으며, 실험결과 분석에서는 목표 파랑제원이 아닌 실험파 설정시의 파랑제원을 이용하여 결과를 분석하였다. 본 실험은 경사식방파제 상치 콘크리트에 작용하는 수평파력을 계측하는 것으로서 유의주기 기준 1,100파를 조파하고, 전반부 100파를 제외한 후반부 1,000파가 작용하는 시간동안에 계측된 자료를 이용하여 파력을 분석한 후, 파압으로 환산하였다.
3.3 실험단면 및 제원본 실험에 적용된 단면은 Fig. 4와 같다. Fig. 4에서 type R0는 경사식방파제 단면에서 피복재가 거치되지 않고, 중간 피복층이 불투과(impermeable)인 단면이고, type R1은 제체 경사면에 테트라포드(tetrapod, TTP)가 피복된 단면으로서 중간피복층은 제체사석 상부에 트라이포드(tripod)가 설치된다. 실험단면에 대한 기하학적 제원을 정리한 것이 Table 2이다. 상치콘크리트 전면의 피복재 어깨폭은 테트라포드가 2열 거치되고, 피복층은 2층인 조건이다. 본 실험에서는 설정된 실험파 조건내에서 피복재의 움직임이 발생되지 않도록 개당 중량이 0.92 kg인 테트라포드를 사용하였다. Fig. 4에서 type R0 단면은 피복층에 의한 에너지감쇄가 없는 조건에서 상치 콘크리트에 작용하는 파력을 계측하기 위한 것이고, type R1 은피복층에 의해 상치콘크리트가 보호되는 보호부 또는 피복부(protected part)와 노출부(unprotected part)에 작용하는 수평파력을 계측하기 위한 것이다. 즉, type R0는 에너지감 쇄가 없는 조건에서 Goda 파압과 비교하기 위한 것이고, type R1은 Goda 파압식에서 파압보정계수를 적용한 파압과 비교하기 위한 것이다. 또한 실험에서 계측된 type R0와 type R1의 파압을 비교하여 피복에 의한 파압과 노출부에 작용하는 파압을 각각 비교하였다. Fig. 5는 Fig. 4에 도시된 실험 모형 설치장면이며, 각 사진의 좌측상단에 계측기가 설치된 장면을 포함하였다. 실험에 사용된 실험수로에서 실험체는 폭 0.8 m 수로구간에 설치되며, 파력계측은 폭 0.8 m의 중앙부 0.3 m 구간에서 계측하였다. 즉, 각각의 수로벽면으로부터 0.25 m 구간에서는 계측을 수행하지 않았다. 이는 수로벽면 효과로 인해 계측에 영향을 미치는 것을 배제하기 위함이다. Fig. 6은 각 단면별 실험장면이며, 실험모형은 조파기로부터약 30 m 거리에 위치한다.
Table 1에 제시된 파랑제원으로 생성된 실험파 제원과 Table 2에 제시된 모형제원으로부터 분석한 상대여유고(RC/H1/3)는 RC/H1/3= 0.99~1.90, 상대피복높이(AC/H1/3)는 AC/H1/3 = 0.74~1.43이다. 따라서 본 실험에 적용된 상대여유고 및 상대피복높이 제원은 일반적인 경사식방파제 설계조건 범위를 포함한다고 할 수 있다.
Fig. 7은 상치콘크리트 전면에 설치되는 파력계의 배치와 파력계측을 위한 패널(panel)을 도시한 것이다. 상치콘크리트 전면에 7개의 패널(PW = 0.3 m(폭), PH = 0.028 m(높이))을설치하였으며, 패널간 간격은 0.002 m를 두어 패널간의 접촉이 없도록 하였으며, 최하단 패널과 중간피복층 상단과도 접촉되지 않도록 하였다. 각 패널에 2개의 파력계(load cell)를 설치하였으며, 전체 14대의 파력계가 활용되었다. Pedersen (1996)과 Nørgaard et al.(2013)은 파압계(pressure gage)를 이용하여 파압을 계측하였다. 파압계를 활용할 경우에 파압계 설치위치별로 서로 다른 파압이 계측되게 된다. 즉, 파압계가 피복재 후면에 위치하는 경우와 공극에 위치하는 경우에 서로 다른 파압이 계측된다. 이를 보완하기 위해 Pedersen (1996)과 Nørgaard et al.(2013)은 상치콘크리트 기준선방향 (파봉선 방향)으로 동일 높이에 대해 노출부에는 2개, 피복부 (보호부)에는 2~3개의 파압계를 설치하여 계측된 각각의 파압을 평균하여 사용하였다. 2~3개의 파압계를 동일 높이에 설치하여 평균하더라도 계측 파압이 적정한가에 대한 의문은 여전히 남게되지만, Pedersen과 Nørgaard et al.은 피복재로 피복석을 이용하였기 때문에 상대적으로 잘 짜여지는 피복석의 특성상 전술한 문제점은 어느 정도 상쇄되었을 것으로 판단된다. 본 연구에서는 공극이 상대적으로 큰 테트라포드를 피복재로 사용하였기 때문에 파압계를 활용했을때의 문제점을 보완하기 위해 일정 면적을 가지는 패널을 설치하고, 패널에작용하는 파력을 계측한 후 파압으로 환산하여 결과를 분석 하였다. 실험단면 type R0의 경우에는 Fig. 7에 도시된 전체 패널(PN01~PN07)이 작용파랑에 직접 노출되며, type R1의 경우에는 PN01~PN05는 피복재로 보호되는 부분의 파력을 계측하고, PN06~PN07은 노출부의 파력을 계측하게 된다.
4. 실험 결과4.1 계측자료 분석본 연구에서는 계측된 파력 중 상위 0.4%에 해당하는 파력을 평균하고 파압(p)으로 환산한 후, 결과분석에 활용하였다. 분석된 파압(p)은 무차원파압(p* = p/ρgH1/3)으로 환산하였으며, 여기서 ρ는 유체의 밀도, g는 중력가속도이고 H1/3은 실험파 설정시의 유의파고이다. 분석된 결과를 도시할 때, 종축은 정수면으로부터 계측점까지의 높이(z)를 목표 유의파고[(H1/3)t]로 나눈 상대높이[z/(H1/3)t]로 나타내었다. 동일 목표 유의파고인 경우에도 주기별로 설정된 유의파고(H1/3)가 서로 다르기 때문에 z/H1/3로 도시하게 되면 상치콘크리트 전면 계측지점의 상대높이가 약간씩 달라지게 된다. 전술한 바와 같이 결과 분석시에는 설정된 유의파고를 사용하였지만, 결과를 도시할 때는 편의를 위해 목표 유의파고를 이용한 상대높이[z/(H1/3)t]를 활용하였다.
Fig. 8은 피복재가 거치되지 않고, 제체사석 상부가 불투과 사면인 type R0 단면에서 계측된 파압과 Goda(1974, 2010) 파압산정식의 결과를 비교한 것이다. Fig. 8(a)는 (H1/3)t = 0.12 m인 조건에 대해 유의주기별 결과를 비교한 것으로 상치콘크리트 전면 하부에서 상부쪽으로 갈수록(즉, z/(H1/3)t가 커질수록) 파압이 감소하는 경향은 동일하지만 계측결과(measured data)가 Goda 식에 의한 파압에 비해 약 2배 정도 크게 나타났다. Fig. 8(b)와 (c)는 각각 (H1/3)t = 0.16 m와 0.2 m의 결과로서 입사파고가 증가함으로 인해 상당히 큰 파압이 상치콘크리트에 작용하는 것으로 계측되었으나, Goda 파압산정식에 의한 결과는 계측결과와 큰 차이를 보이며 연직 분포 또한 뚜렷한 차이를 보인다. Goda 파압결과는 파고의 크기에 관계없이 상치콘크리트 상부로 갈수록 선형적으로 감소하는 반면, 계측결과에서는 (H1/3)t = 0.16 m인 경우에는 상치콘크리트 중앙부, (H1/3)t = 0.20 m에서는 상부에 큰 파압이 작용함을 알 수 있다. Goda 파압식은 직립벽에 대한 산정식인데 반해, 경사제의 경우에는 사면을 따라 처오르는 파랑으로 인해 상치콘크리트에 큰 파압이 작용하는 것으로 판단된다. 특히 입사파의 주기가 길어질수록 처오름높이가 증가함으로 인해 이러한 경향은 보다 뚜렷하게 나타났다.
Fig. 9는 제체사면 상부에 피복재가 피복된 조건인 type R1 단면에서 계측된 파압과 피복재 피복에 따른 Takahashi et al.(1990)의 파압보정계수를 적용한 Goda 파압산정 결과를 비교한 것이다. 피복재가 피복되지 않은 type R0 결과인 Fig. 8과 비교해볼 때 피복구간(보호부 구간)의 파압은 감소하지만, 노출부의 경우에는 상당히 큰 파압이 작용함을 알 수 있다. 보호부(피복부)에 대한 계측결과와 파압보정계수를 적용한 Goda 파압산정 결과는 입사파의 주기가 짧은 경우에는 비교적 근사하지만, 주기가 길어질수록 계측결과가 크게 나타난다. 노출부(미피복부)의 경우에는 상당히 큰 파압이 작용하고 있음을 확인할 수 있으며, 이 또한 주기가 길어질수록 그차이는 커진다. Fig. 9에서 보호부 구간 중 최상단 구간(Fig. 7의 PN05, 즉 노출부와 인접 구간)은 보호부 구간임에도 불구하고 타 보호부 구간에 비해 상당히 큰 파압이 작용함을 알수 있다. 본 연구에서 수행한 실험파의 유의주기 범위내에서 상대적으로 짧은 주기에서는 보호부와 인접한 노출부(Fig. 7 의 PN06, 즉 보호부와 인접 구간)보다 큰 파압이 작용하는 경우도 있으며, 주기가 길어지게 되면 노출부의 파압이 상대적으로 더 크게 계측되었다. 이는 내습파가 사면을 따라 처오른 후 상치콘크리트 전면에 피복된 피복재 어깨 상부에서 아랫방향으로 강한 파력이 작용하기 때문으로 판단되며, 주기가 길어지게 되면 파의 처오름높이가 상대적으로 더 높아지기 때문에 보호부보다는 노출부에 작용하는 파압이 더 큰것으로 생각된다. 전술한 바와 같이 Fig. 9는 국내에서 경사식방파제 상치콘크리트 설계시 사용하는 파압산정법(즉, Goda 파압식에 파압보정계수를 적용한 파압)의 결과와 본 연구에서 계측한 파압을 비교한 것으로 국내 설계법에 의한 파압이 상당히 과소하게 산정되고 있음을 알 수 있으며, 특히 노출부에 작용하는 파압의 차이는 보다 더 크게 나타나고 있다. 이러한 파압의 과소평가는 상치콘크리트의 활동, 전도 피해를 야기할 수 있으며, 상치콘크리트의 활동, 전도는 피복재의 유실로 이어지게 된다.
Fig. 10은 피복재가 피복된 단면(type R1)에서 계측된 파압을 미피복 단면(type R0)의 계측결과로 나누어 도시한 것이다. Fig. 10(a)는 (H1/3)t = 0.12 m의 결과로서 피복부의 상단과 노출부의 상단 구간에서 미피복시보다 더 큰 파압이 작용함을 알 수 있으며, 미피복시보다 2배 이상의 파압이 작용하는 조건도 나타난다. 이는 피복재가 피복됨에 따라 피복재 상부를 따라 처오름이 발생함으로 인해 미피복시보다 높은 위치의 상치콘크리트 구간에 파랑이 작용하기 때문으로 판단된다. 이러한 현상은 주기가 긴 경우에 뚜렷하게 나타나며, 이는 동일 파고조건이라 하더라도 주기가 길어짐에 따라 처오름이 증가하기 때문이다. Fig. 10(b)와 10(c)는 각각 (H1/3)t = 0.16 m와 0.20 m의 결과를 비교한 것으로서 파고가 증가할수록 (H1/3)t = 0.12 m에서 나타난 현상은 감소하게 된다. 일부 조건에서 미피복시(type R0)의 경우보다 큰 파압이 계측되었지만, 이는 주기가 상대적으로 짧은 조건으로서 피복층 설치 여부에 따른 처오름높이의 변화에 기인하는 것으로 판단된다.
4.2 파압보정계수 제안4.1절에서는 상치콘크리트에 작용하는 수평파압 산정시 Goda 파압식(1974, 2010)과 Takahashi et al.(1990)의 파압 보정계수를 이용하는 것은 파압이 과소 평가됨을 보였다. Goda 파압산정식을 이용하는 것보다는 상치콘크리트에 작용하는 파압을 직접 산정할 수 있는 경험식을 제안하는 것이 타당하지만, 제한된 실험조건의 결과만으로는 한계가 있어 향후 과제로 미루고 보완실험을 통한 자료확보 후 제안하는 것을 계획하고 있다. 따라서 본 연구에서는 Goda 파압산정식을 기본으로 하고, 전사면 피복 혼성제에 작용하는 파압산정 식에 적용하는 Takahashi et al.(1990)의 파압보정계수(λ)가아닌 새로운 파압보정계수를 제안하고자 한다. Takahashi et al.의 파압보정계수는 식(2)와 같이 H/d에 따라 주어지고 주기의 함수는 아니다. 본 연구에서는 입사파의 주기에 따라 파압의 크기가 달라지는 것을 확인하였으므로 H/d와 주기의 영향을 포함하는 파압보정계수를 제안하고자 한다.
Figs. 8~10은 보호부와 노출부에 설치된 각 패널에서 계측된 파압을 제시함으로서 연직방향의 파압분포를 알 수 있었다. 상치콘크리트 전면 연직방향의 파압분포는 유사한 경향을 보이지만 피복부(보호부)와 노출부 구간내의 높이(위치)별 파압조정계수를 산정하는 것은 상당히 어려운 문제라고 판단된다. 따라서 본 논문에서는 Fig. 7에 도시된 보호부(피복부)인 PN01~PN05와 노출부인 PN06~PN07에서 계측된 파압을 각각 평균하여 보호부와 노출부에 대한 파압보정계수를 구분하여 제시하는 것으로 계획하였다.
Fig. 11은 파압보정계수를 적용하지 않은 Goda 파압과 피복된 단면(type R1)에서 계측된 파압 자료를 이용하여 보호부(피복부)와 노출부의 평균파압을 도시한 것이다. 전체적으로 입사파의 주기가 길어질수록 파압이 증가하는 일반적인 경향을 보인다. 보호부 구간을 살펴보면, 주기가 상대적으로 짧은 조건에서는 파압보정계수를 적용하지 않은 Goda 파압과 피복된 단면에서 계측된 파압이 유사하게 나타나지만, 주기가 길어질수록 계측 파압이 크게 나타남을 알 수 있다. 노출부 구간의 경우에 Goda 파압식의 특성으로 인해 보호부 구간보다 작게 산정되지만, 계측자료는 보호부 구간의 평균 파압보다 크게 나타난다. 이러한 경향은 주기가 길어질수록 명확하다. 파고가 작고 주기가 짧은 조건에서 노출부 구간의 평균파압은 보호부 구간의 1.5배 이하로 나타나지만, 파고가 커 지거나 주기가 증가하게 되면 2배 내외에 달하는 것으로 분석되었다. 이러한 경향은 (H1/3)t = 0.20 m 조건의 결과인 Fig. 11(c)를 살펴보면 뚜렷하다.
Fig. 12는 본 연구의 구간별(노출부, 보호부) 평균파압과 Pedersen(1996) 및 Nørgaard et al.(2013)의 산정식에 의한 결과를 비교한 것이다. Fig. 12(a)는 노출부 구간으로서 본 연구에 비해 Pedersen의 결과는 상당히 크게 산정되며, Nørgaard et al.의 결과도 약간 크지만 그 차이는 크지 않다. Fig. 12(b) 는 보호부 구간으로서 Nørgaard et al.의 결과는 본 실험결과와 유사한 반면, Pedersen의 결과는 작게 산정된다. 따라서 전체적으로 본 연구결과와 Nørgaard et al.의 결과가 유사하게 나타났다. 그러나 Fig. 12에서 전체적으로 자료의 분산이 큰 것을 확인할 수 있다. 이는 본 연구에 적용된 파랑 및 단면의 기하학적 제원이 Pedersen(1996) 및 Nørgaard et al.(2013)의 적용범위를 벗어난 조건을 다수 포함하고 있기 때문이다.
Fig. 13은 Pedersen(1996) 및 Nørgaard et al.(2013)의 적용범위에 상당부분 부합되는 조건의 결과만을 비교한 것이다. Fig. 13(a)는 노출부 구간으로서 본 연구와 Nørgaard et al. 의 결과는 부합되는 반면, Pedersen의 결과는 상당히 큰 파압이 산정되었다. 이는 Nørgaard et al.이 지적한 바와 같이 Pedersen의 산정식은 노출부 파압을 과대평가하기 때문으로 판단된다. Fig. 13(b)는 보호부 구간으로서 Pedersen 및 Nørgaard et al.의 산정결과는 본 연구보다 파압을 작게 예측하고 있다. 이는 크게 두가지 차이점 때문으로 판단된다. 첫번째는 파력을 계측한 방법과 파압을 계측한 방법의 차이이며, 두 번째는 적용 피복재의 차이에 기인하는 것으로 생각된다. Pedersen 및 Nørgaard et al.은 피복석을 적용하였고, 본 연구는 테트라포드를 적용함으로서 두 피복재의 거치방법 및 공극의 차이가 존재하기 때문이다.
전체적으로 노출부 구간은 기존 연구결과와 유사하고, 보호부 구간은 다소 크게 파압이 산정되지만 차이가 발생하는 이유는 충분한 근거가 있다고 판단된다. 따라서 본 연구에서 수행한 결과는 신뢰할 수 있다고 판단되며, 본 연구의 실험 결과를 이용하여 파압보정계수를 분석하였다.
본 연구에서는 type R1 단면에 대해 계측된 파압을 파압 보정계수를 적용하지 않은 Goda 파압으로 나누어 실험조건별 파압비를 산정한 후, 노출부와 보호부(피복부) 구간의 파압보정계수를 회귀식을 이용하여 각각 도출하였다.
Fig. 14는 경사식방파제 상치콘크리트에 작용하는 수평파압을 산정하기 위한 Goda 파압산정식의 파압보정계수(λnew) 산정결과를 도시한 것이다. 그림에서
식(8)에서 0.2σ 만큼 상향된 파압보정계수 산정식은 식(9)와 같다. 여기서, σ는 실험자료의 표준편차이다.
본 연구에서는 상치콘크리트 안정성 확보측면에서 식(9)를 Goda 파압식의 파압보정계수로 제안하고자 한다.
Fig. 15는 실험결과와 식(8) 및 식(9)로부터 산정된 파압보 정계수를 이용하여 Goda 파압식으로부터 산정된 파압을 비교한 것으로 노출부 및 보호부 구간 모두 계측파압과 산정파압이 잘 일치함을 확인할 수 있다. 그리고 본 연구의 회귀식(regression formula, 식(8))을 적용한 결과와 제안식(proposed formula, 식(9))을 적용한 결과의 차이는 크지 않다.
5. 결론경사식방파제 설계시 상치콘크리트에 작용하는 수평파압을 산정한 후, 상치콘크리트의 활동 및 전도가 발생되지 않도록 설계하여야 한다. 국내에서는 이러한 수평파압 산정식이 부재함으로 인해 Goda 파압산정식에 전사면 피복 케이슨 혼성제에 적용하는 파압보정계수를 이용하여 수평파압을 산정하여 왔다. 본 연구에서는 현재 국내에서 적용하고 있는 문제점을 확인하고, 경사식방파제의 상치콘크리트에 작용하는 수평파압 산정을 위해 새로운 파압보정계수를 도출하기 위한 2차원 수리실험을 수행하였으며, 도출된 결과를 요약하면 다음과 같다.
(1) 국내에서는 경사식방파제 상치콘크리트 설계시, Goda 파압식(1974, 2010)을 이용하여 상치콘크리트에 작용하는 수평파압을 산정하고 있으나 노출부 구간에서의 파압을 상당히 과소평가함을 확인하였다.
(2) 보호부(피복부) 구간의 경우에도 Takahashi et al.(1990)의 파압보정계수를 이용한 Goda 파압도 과소하게 산정되는 것으로 나타났다.
(3) 상치콘크리트에 작용하는 수평파압 산정을 위한 Goda 파압식의 파압보정계수를 노출부와 보호부에 대해 쇄파매개변수와 상대파고의 함수로 각각 제안하였다.
본 연구에서는 실험결과를 이용하여 경사식방파제 상치콘크리트에 작용하는 파압산정시 적용할 수 있는 Goda 파압식의 파압보정계수를 제안하였다. 그러나 다양한 조건에 대한 지속적인 실험을 수행하여 Pedersen(1996) 및 Nørgaard et al.(2013)이 제안한 것과 같은 상치콘크리트에 작용하는 수평 파압을 직접 산정할 수 있는 제안식의 도출이 최종 목표이다. 이를 위해 현재 상치콘크리트 전면 피복재의 어깨폭 변화에 따른 파압특성에 대한 실험을 수행하고 있으며, 그 결과는 후속 논문으로 발표할 예정이다.
Fig. 12.Comparison of the measured data with the calculation by Pedersen (1996) and Nørgaard et al. (2013). 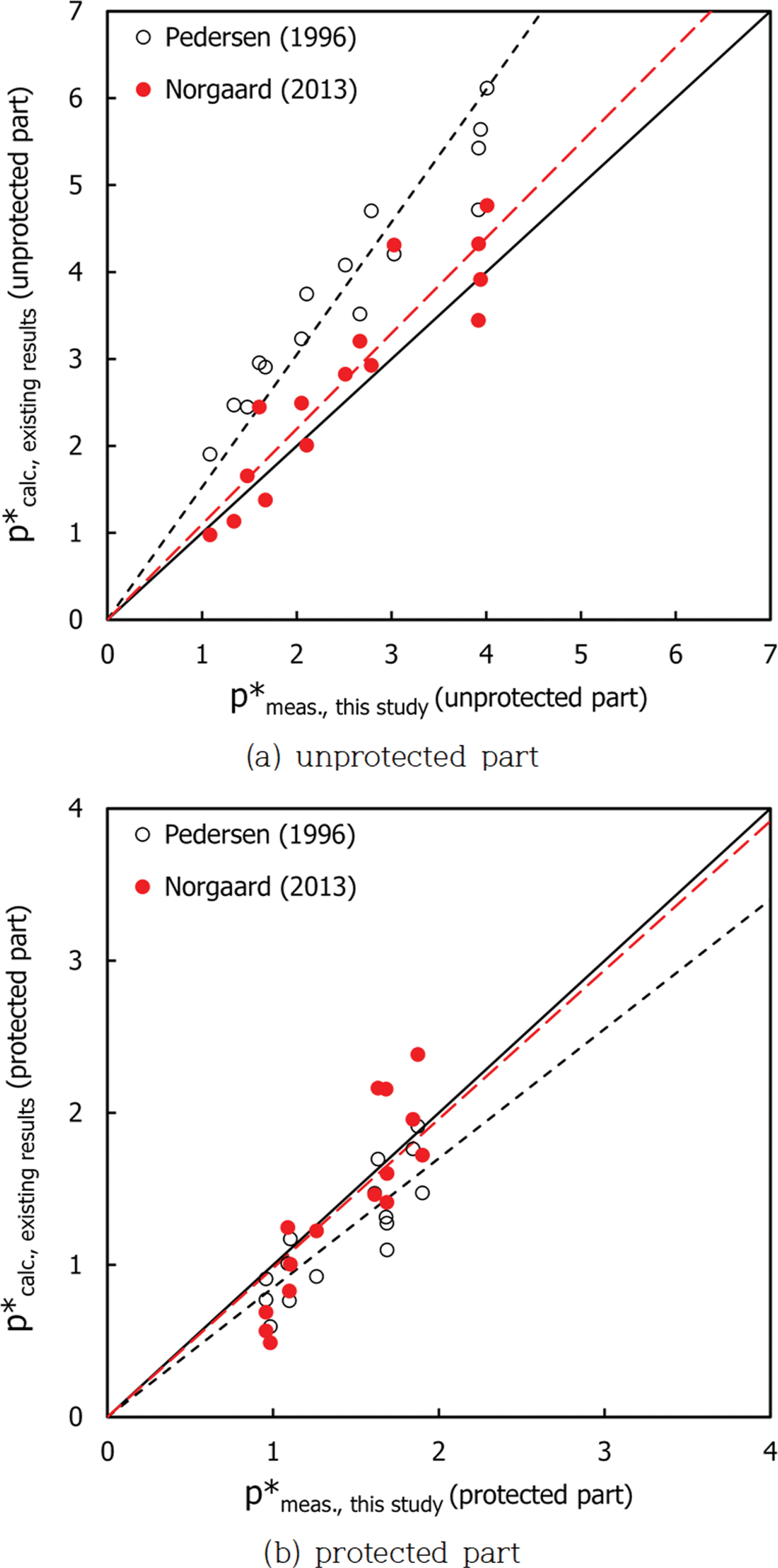
Fig. 13.Comparison of the measured data with the calculation by Pedersen (1996) and Nørgaard et al. (2013) within the parameter ranges of this experiments. 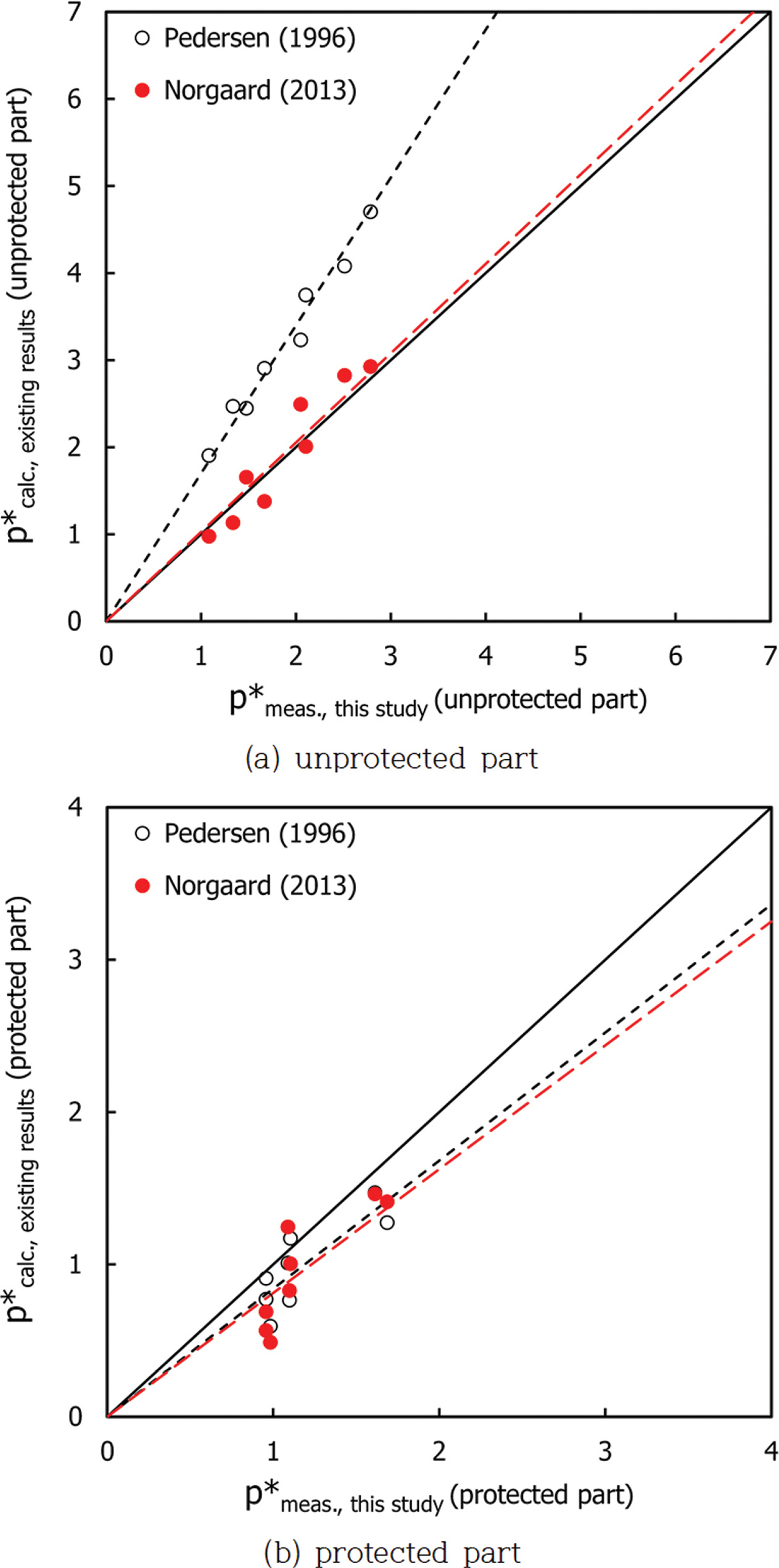
ReferencesAniel-Quiroga, í., Vidal, C., Lara, J.L., González, M (2019). Pressures on a rubble-mound breakwater crown-wall for tsunami impact, Coastal Engineering, 152, 543-558.
Chen, X., Hofland, B., Altomare, C., Suzuki, T., Uijttewaal, W (2015). Forces on a vertical wall on a dike crest due to over-topping flow, Coastal Engineering, 95, 103522.
Contestabile, P., Iuppa, C., Lauro, E.D., Cavallaro, L., Andersen, T.L., Vicinanza, D (2017). Wave loadings acting on innovative rubble mound breakwater for overtopping wave energy conversion, Coastal Engineering, 122, 60-74.
Doorslaer, K.V., Romano, A., Rouck, J.D., Kortemhaus, A (2017). Impacts on a storm wall caused by non-breaking waves overtopping a smooth dike slope, Coastal Engineering, 120, 93-111.
Formentin, S.M., Palma, G., Zanuttigh, B (2021). Integrated assessment of the hydraulic and structural performance of crown walls on top of smooth berms, Coastal Engineering, 168, 103951.
Goda, Y. (1974). New wave pressure formulae for composite breakwaters, Proceedings of the 14th Coastal Engineering Conference, ASCE. 1702-1720.
Goda, Y. (2010). Random seas and design of maritime structures. World Scientific, Singapore: ISBN 978-981-4282-39-0.
Guanche, R., Losada, I.J., Lara, J.L (2009). Numerical analysis of wave loads for coastal structure stability, Coastal Engineering, 56, 543-558.
Jacobsen, N.G., van Gent, M.R.A., Capel, A., Borsboom, M (2018). Numerical prediciton of integrated wave loads on crest walls on top of rubble mound structures, Coastal Engineering, 142, 110-124.
Martin, F.L., Losada, M.A., Medina, R (1999). Wave loads on rubble mound breakwater crown walls, Coastal Engineering, 37, 149-174.
Molines, J., Herrera, M.P., Medina, J.R (2018). Extimations of wave forces on crown walls based on wave overtopping rates, Coastal Engineering, 132, 50-62.
Nørgaard, J.Q.H., Andersen, T.L., Burcharth, H.F (2013). Wave loads on rubble mound breakwater crown walls in deep and shallow water wave conditions, Coastal Engineering, 80, 137-147.
Pedersen, J. (1996). Wave forces and overtopping pn crown walls of rubble mound breakwaters, Ph.D. thesis, Series paper 12, ISBN 0909-4296. Hydraulics & Coastal Engineering Lab., Dept. of Civil Engineering, Aalborg University; Denmark.
Takahashi, S, Tanimoto, K, Shimosako, K. (1990). Wave and block forces on a caisson covered with wave dissipating blocks. Report: Port and Harbour Research Institute, Yokosuka, Japan: p 3-34.
van der Meer, J.W., Stam, C.J.M (1992). Wave run-up on smooth and rock slopes, J of Waterways, Port, Coastal and Ocean Engineering, 188(5):534-550.
|
|