요약하중·저항계수 설계는 일관된 시스템적 설계해를 제공하는 효율적인 설계 방식이다. 이 연구는 확률론적 프레임워크 내에서 방파제의 지반기초(foundation) 설계에 필요한 하중계수 및 저항계수를 결정하는 것을 목표로 하여 한국형 방파제의 대표적인 4가지 유형인 경사식 방파제, 무공케이슨 혼성식방파제, 유공케이슨 혼성식방파제, 소파블록 피복제를 대상으로 조사하였다. 파랑하중조건에서 방파제 기초의 지지력을 면밀히 조사하였다. 100,000회 샘플에 의한 Monte Carlo 시뮬레이션을 사용하여, 목표신뢰도지수(RI) 2.5와 3.0의 두 가지 수준을 선택하여 하중·저항계수의 보정을 수행하였다. 예상대로 더 높은 RI에 대해 정규화된 저항계수는 더 낮은 값을 갖는 것으로 확인되었다. 그 범위는 목표 RI 2.5의 경우 0.668~0.687이며, 목표 RI 3.0의 경우 0.576~0.634이다.
AbstractLoad and resistance factor design is an efficient design approach that provides a system of consistent design solutions. This study aims to determine the load and resistance factors needed for the design of breakwater foundations within a probabilistic framework. In the study, four typical types of Korean breakwaters, namely, rubble mound breakwaters, vertical composite caisson breakwaters, perforated caisson breakwaters, and horizontal composite breakwaters, are investigated. The bearing capacity of breakwater foundations under wave loading conditions is thoroughly examined. Two levels of the target reliability index (RI) of 2.5 and 3.0 are selected to implement the load and resistance factors calibration using Monte Carlo simulations with 100,000 cycles. The normalized resistance factors are found to be lower for the higher target RI as expected. Their ranges are from 0.668 to 0.687 for the target RI of 2.5 and from 0.576 to 0.634 for the target RI of 3.0.
1. IntroductionIn load and resistance factor design (LRFD), load and resistance factors (LRFs) are calibrated based on acceptable safety levels (i.e., target reliability index (RI) or target probability of failure (PF)) for practical design. Historically, LRFs are commonly determined by the mean-value first-order second-moment (MVFOSM) method or the first-order reliability method (FORM) adopting a close form solution. The aforementioned methods provide efficient approaches for reliability analysis where the performance function is defined explicitly. However, they are inapplicable for limit state functions defined in an implicit fashion. In slope stability analysis, the finite element method or the limit equilibrium method (LEM) is commonly utilized. Thus, the safety factor is found in an implicit manner.
The breakwater (BRW) structures and their soil foundations must be designed such that the foundations are safe enough to carry the superstructures during their lifetime. The bearing capacity of the foundation under the wave loading condition is one of three common conditions that need to be verified during the design of the breakwater foundations (MLIT, 2009). Wave forces acting on the breakwaters include horizontal and vertical components. Due to the wave forces acting on the caisson blocks, the foundations are induced an eccentric and inclined loading. Hence, the failure modes are depicted by the bearing capacity of the soil foundations. In the practical design of breakwater foundations, the LEMs are frequently applied. Pertaining to LEM, Bishop’s simplified method (BSM) is recommended as a suitable method to evaluate the stability of the foundation under eccentric and inclined loading (MLIT, 2009). The factor of safety using BSM is not only defined implicitly but also exhibits non-linearity. This feature restricts the application of MVFOSM or FORM to reliability analysis.
Monte Carlo simulation (MCS) is a robust method to assess the system reliability of almost all engineering problems. It is the best choice for problems dealing with implicit limit state functions, for instance, determination of safety factor in the slope stability analysis. Thus, in this study, MCS is employed for both reliability analysis and calibration of LRFs. Before the calibration of LRFs, the target RI should be specified. Generally, the target RI is governed by the balance of acceptable investment cost, and the associate risk and it is not the scope of this study. In the present work, two target reliability indexes of 2.5 and 3.0 are chosen for the LRFs calibration. Based on the specified target RIs, the MCS-based LRFs calibration is performed.
Four different types of breakwaters (BRW), as shown in Fig. 1, including the rubble mound BRW (RBRW), the vertical composite BRW (VBRW), the perforated caisson BRW (PBRW), and the horizontal composite BRW (HBRW), are examined. Three sections for each type, making up twelve case studies, are considered in this study. Within the MCS-based LRFs calibration framework, the nominal values of input variables are adjusted. The system RI is then evaluated for the corresponding adjusted problem. This trial process is repeatedly conducted until the system RI is close enough to the target RI. Finally, the LRFs are determined based on the calibrated problem consisting of the searched nominal input variables.
2. Method2.1 Limit state function for the bearing capacity of breakwater foundation under wave loadingIn the conventional deterministic approach, either the finite element methods or the limit equilibrium methods can be conducted to assess the stability of the slope. MLIT (2009) recommends that Bishop’s simplified method, one of the well-known LEMs, can be adopted to evaluate the stability of slope foundation and to verify the bearing capacity of BRW’s foundation. It is worth noting that the excitation of wave forces causes an eccentric and inclined loading to the BRW’s foundation, and the safety factor must consider the wave forces. The safety factor of the foundation under the wave loading is presented in Eq. (1). In Eq. (1), w' and w are the effective weight and total weight of the comprising slice segment, respectively. qEx is the vertical surcharge load distributed on the slice. Fh and a correspond to the horizontal wave force and its lever arm about the failure center. R is the radius of the considered failure surface. c is the apparent cohesion of the soil (or undrained shear strength in the case of cohesive soil), and ϕ is the friction angle of the soil along the base surface of each slice. s is the width of each slice. Finally, θ is the inclination angle horizontal to the base surface.
The limit state function, g based on the safety factor is defined by Eq. (2). The limit state function divides the input variable space into the safety and failure zones. In this study, the safety zone is depicted by the zone that includes the non-negative values of g and the failure zone consists of the negative values of g. The limit state function is defined implicitly because the FS term is implicit, as presented in Eq. (1).
2.2 Reliability analysisThe statistical information of the random input variables is collected from the design documents and listed in Table 1. In the assessment of foundation bearing capacity, the uncertainties consist of three types of variables, namely, the variables governed by an upper structure such as weights of structural components; the variables related to the ocean condition (i.e., tide level, wave condition); and the uncertainties in the soil foundations (soil weight and shear strength parameters). The uncertainties are depicted by the bias factors, defined as the ratio of the mean values and the nominal values. All uncertain input variables are assumed to have normal distributions in this study.
As can be seen in Eqs. (1) and (2), the limit state function is evaluated based on an implicit fashion of the safety factor function. Thus, the application of MVFOSM or FORM becomes difficult because the derivatives are involved. Monte Carlo simulation is, however, can be straightforwardly performed (Doan et al., 2020). In the MCS, the input variables are sampled using their distributional information, and then the limit state functions are evaluated using the samples. After the simulation, the population of limit state function g is determined. The probability of failure PF is then calculated as the ratio of the number of failure events N Fails and the total size of MCS NMCS as shown in Eq. (3). A failure event locates in the failure zone and is counted whenever the value of its limit state function g is negative. The cycles of MCS is set as 100,000 in this study. The COV of the PF from MCS, COVPf, can be determined using Eq. (4) (Haldar and Mahadevan, 2000).
Based on the PF result from the MCS, the corresponding reliability index can be approximated using Eq. (5). The term Φ in Eq. (5) is the cumulative probability density of the standard normal distribution.
2.3 Calibration of load and resistance factorsUnder the same probabilistic condition, the different designs will obtain different results of PF and RI. Additionally, in the LRFs calibration, the systems need to be calibrated such that their system PF and RI meet the target values of PF and RI. The abovementioned concepts imply that in the calibration process, the input parameters of the system need to be adjusted to achieve a specified target PF or RI. For example, if the reliability index of the existing design is greater than the target value (i.e., over-designed structure), it means either the factors governing the resistance component can be reduced or the factor controlling the load terms can be increased. Fig. 2 presents the concept of LRFs calibration. From the figure, all of the realizations at the existing condition lie on the safety zone, implying a high value of RI. Then during the calibration condition, the realizations move upward, resulting from the adjustment of input variables.
The estimated RI is compared to the target RI to check the convergence for every trial step during the calibration process. If the estimated RI does not meet the target value, the input variables are amended and the system RI is then again evaluated (Salgado and Kim, 2014). This routine is repeated until the convergence condition is satisfied. In the present work, the tolerance of PF is set as 5% to be the convergence condition. In order to have a more effective adjustment of the input variables, the sensitivity analysis conducted in the authors’previous study (Doan et al., 2021) is employed in this work. After the sensitivity analysis, the dominant variables that have a significant contribution to the limit state function of the systems are selected as the adjusted variables. The minor effect variables resulting from the sensitivity analysis are kept the same as the existing condition. Once the appropriate nominal input values have been found, the load factor LF and resistance factor RF can respectively be determined using Eq. (6) (Salgado and Kim, 2014).
In Eq. (6), R and Q are resistance and load components. n stands for the nominal value, and the asterisk stands for the limit values. It should be noted that the nominal values and the limit values used in Eq. (6) are assessed from the successive calibration process for each safety level. The limit points are defined as those that lie close to the limit surface. In this study, the cases with the safety factors between 0.99 and 1.01 are counted as limit points. This definition of limit points was employed in our previous study (Doan et al., 2021). The load and resistance factors are determined as the average using all considered limit state points.
Uncertainties of the input variables are commonly simulated by bias factors. The bias factors are defined as the ratio of the measured and nominal values. The bias factor with a value lower than unity implies that the nominal parameter is over-predicted. Thus, a reduction needs to be applied. For instance, the wave forces are commonly overestimated using Goda’s formulations (Goda, 2000; MLIT, 2009); therefore, bias factors with a value lower than the unity of the wave forces need to be applied to precisely mimic the actual situation. In addition, the statistical properties of bias factors for wave forces are different for each superstructure type. The statistical properties of the considered uncertainties are presented in Table 1. Three sections of four different types of breakwaters located around South Korea are opted to be the case studies. Accordingly, 12 different case studies are listed in Table 2, including six BRWs located in the east; four BRWs in the south; two sections in the west, are considered. The tide variation is differently considered for different shorelines.
3. Results and Discussions3.1 Results of reliability analysis for the existing structuresThe reliability analysis is first performed for twelve cases using the MCS discussed in Section 2. The results of the reliability indexes of the existing structures are presented in Fig. 3. It can be seen that at the initial condition, the rubble mound breakwaters and the horizontal composite breakwaters are designed in safer situations than the perforated breakwaters and vertical composite breakwaters.
3.2 Results of the calibrated load and resistance factorsUsing the MCS-based calibration process of LRFs, the system reliability indexes of the twelve cases are shown in Fig. 4 for two levels of the target RIs. It can be seen that after the calibration, the system RIs of all considered cases are almost identical to the target values.
The calibrated load and resistance factors are determined using Eq. (6) and are illustrated in Fig. 5 and Fig. 6 for the target RI of 2.5 and 3.0, respectively. It is clearly seen that the calibrated resistance factors are generally lower than unity. However, the calibrated load factors are not always greater than unity.
The normalized resistance factors RFn determined by the ratio between RF and LF are shown in Fig. 7 for the two target RIs of 2.5 and 3.0.
By assuming load factors equal to unity, the normalized resistance factors provide consistent insight into both load and resistance factors for every considered case. The mean values of the normalized resistance factors are listed in Table 3 for the two levels of RIs. It can be seen that the RFn ranges from 0.668 to 0.687 for the target RI of 2.5, whereas RFn ranges from 0.576 to 0.634 for the target RI of 3.0. The normalized RF is known to be inversely related to the safety factors from the conventional design. Besides, the RI also exhibits a positive correlation with FS. Hence, as expected, the normalized resistance factor is lower for the higher level of RI and vice versa. Moreover, Fig. 7 illustrates that the rubble mound and the horizontal composite breakwaters exhibit a wider dispersion of RFn compared to the others.
In the conventional design approach, the safety factors reflect the safety level of the design solutions. Alternatively, the reliability index presents the safety level in the probabilistic method. Generally, the two mentioned terms are positively correlated. Though the reliability indexes of the existing designs are different for the twelve cases, as can be seen in Fig. 3, the normalized resistance factors, on the other hand, seem to converge for each target RI as presented in Table 3. This phenomenon implies that the limit state design approach might provide a more consistent design than the conventional design approach. Accordingly, the investment cost might be proportioned appropriately. Thus, it is expected that the calibrated load and resistance factors can be used in the design of the breakwater foundation.
4. ConclusionsIn this study, twelve BRWs of the four different superstructure types are investigated for the bearing capacity of the BRW foundation under the wave loading condition. The fully probabilistic approach of Monte Carlo simulation is applied for reliability analysis. First, the reliability indexes of the existing sections are assessed. Among the four types considered, the rubble mound breakwaters have the highest reliability index, and the perforated caisson breakwaters have the lowest reliability indexes. This result implies that the current design approach using the same specified safety factor of 1.30 does not ensure a consistent and uniform design. Then, all the cases are calibrated to have the RI of 2.5 and 3.0. Based on the successful calibration, the load and resistance factors are evaluated for each safety level. It is demonstrated that the normalized resistance factors are lower for higher target reliability indexes and vice versa. Moreover, compared to RIs of the existing BRWs, the normalized resistance factors exhibit more consistent values after being calibrated. This phenomenon illustrates that the LRFD approach is superior to the conventional design approach by providing consistent resistance factors that ensure construction cost-effectiveness. Finally, RFn ranges from 0.668 to 0.687 for the target RI of 2.5, whereas RFn ranges from 0.576 to 0.634 for the target RI of 3.0.
감사의 글This research was a part of the project titled ‘Development of Design Technology for Safe Harbor from Disasters’, funded by the Ministry of Oceans and Fisheries (20180323), Korea.
Fig. 1.Typical cross-sections of BRWs: (a) the rubble mound breakwater; (b) the vertical composite caisson breakwater; (c) the perforated caisson breakwater; (d) the horizontal composite breakwater. 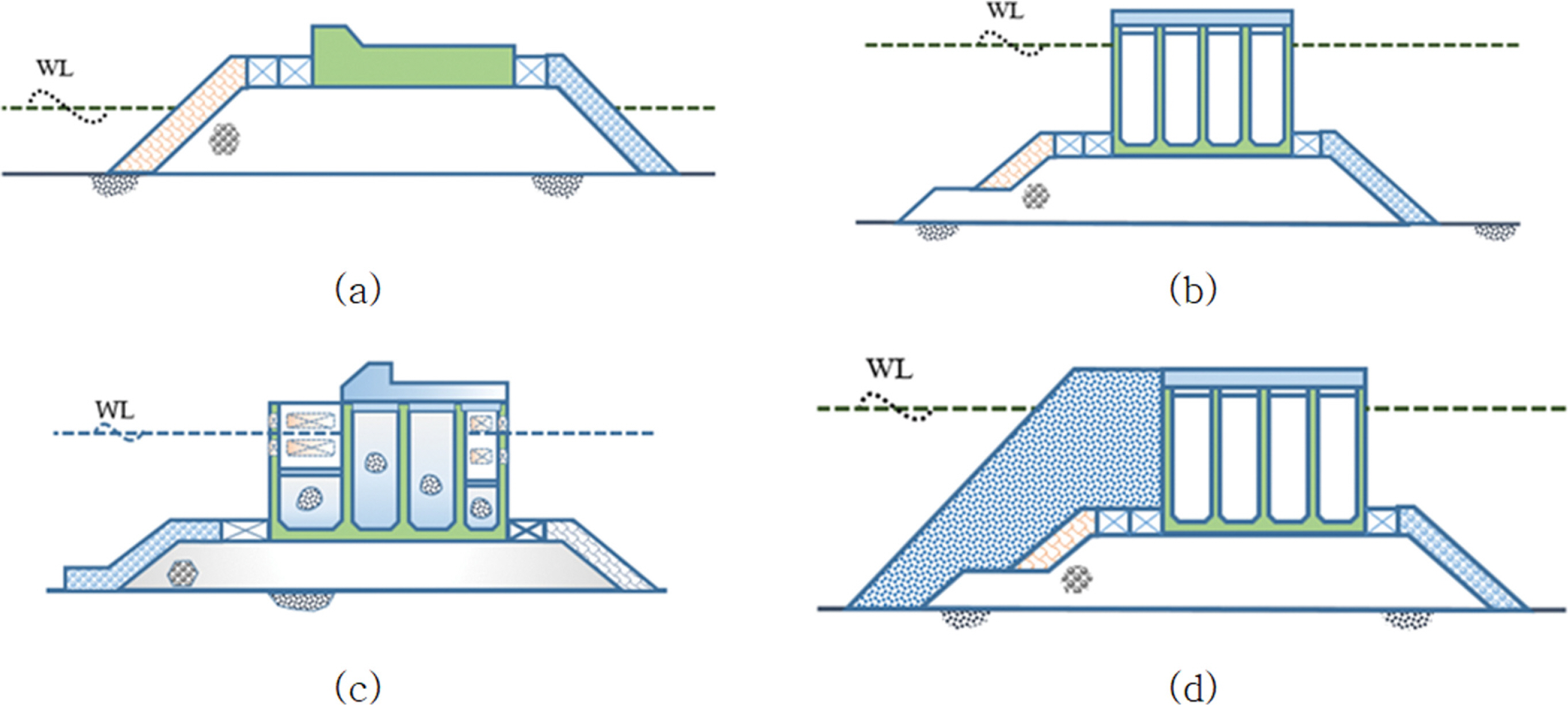
Table 1.Statistical properties Table 2.Case studies ReferencesDoan, NS, Huh, J, Mac, VH, Kim, D, Kwak, K (2020). Probabilistic risk evaluation for overall stability of composite caisson break waters in Korea, J Mar Sci Eng, 8, 1-19 https://doi.org/10.3390/jmse8030148.
Doan, N.S., Huh, J., Mac, V.H., Kim, D.H., Kwak, K (2021). Calibration of Load and Resistance Factors for Breakwater Foundations under the Earthquake Loading, Sustainability, 13, 1730 https://doi.org/10.3390/su13041730.
Goda, Y. (2000). Random seas and design of maritime structures. University of Tokyo Press.
Haldar, A, Mahadevan, S. (2000). Probability, Reliability and Statistical Methods in Engineering Design, Journal of Structural Engineering. John Wiley, Hoboken, NJ, USA.
MLIT. (2009). Technical standard and commentaries for port and harbor facilities in Japan, Ministry of Land, Infrastructure, Transport and Tourism (MLIT). Ports and Harbors Bureau, Tokyo, Japan.
Salgado, R, Kim, D (2014). Reliability analysis of load and resistance factor design of slopes, J Geotech Geoenvironmental Eng, 140, 57-73 https://doi.org/10.1061/(asce)gt.1943-5606.0000978.
|
|
|||||||||||||||||||||||||||||||||