요약해양 이상 자료 탐지의 연구는 이전부터 활발하게 이루어지고 있으며, 통계 및 거리 기반의 기계 학습 알고리즘을 활용하는 기법들이 개발되었다. 최근에는 AI 기반의 해양 자료 이상 탐지 기법이 많은 관심을 받고 있으며, AI를 활용한 해양 이상 자료 탐지 기법은 정답이 주어지는 지도학습 기법이 주를 이루고 있다. 이러한 방법은 학습에 필요한 모든 자료에 수작업으로 분류 정보(라벨)를 지정해야 한다는 점에서 많은 시간과 비용이 요구된다. 본 연구에서는 이러한 문제를 극복하기 위해 비지도학습 기반의 오토인코더를 이상 자료 탐지 기법에 사용하였다. 실험으로는 오토인코더의 평가를 위해 단변수·다변수학습 두가지 실험을 구성하였고, 단변수 학습은 기상청에서 제공하는 덕적도 부이 정점 관측 자료 중 수온만 사용하였으며, 다변수 학습은 수온과 기온, 풍향, 풍속, 기압, 습도 등을 사용하였다. 사용기간은 1996~2020년의 25년간이며 학습 자료에 해양-기상 자료의 특성을 고려한 전처리 기법을 적용하였다. 학습된 다변수와 단변수 오토인코더를 활용하여 실제 표층 수온에 대한 이상 탐지를 시도하였다. 모델 성능 비교를 위해 오차를 삽입한 합성 자료에 다변수와 단변수 오토인코더를 포함한 여러 이상 탐지 기법을 적용하여 정량적으로 평가하였으며, 다변수/단변수의 정확도가 각각 약 96%/91%로써 다변수 오토인코더가 더 나은 이상 자료 탐지 성능을 보였다. 오토인코더를 이용한 비지도학습 기반 이상 탐지 기법은 주관적 판단에 의한 오류와 자료 라벨링에 필요한 시간과 비용을 줄일 수 있다는 점에서 다양하게 활용될 것으로 판단된다.
AbstractOutlier detection research in ocean data has traditionally been performed using statistical and distance-based machine learning algorithms. Recently, AI-based methods have received a lot of attention and so-called supervised learning methods that require classification information for data are mainly used. This supervised learning method requires a lot of time and costs because classification information (label) must be manually designated for all data required for learning. In this study, an autoencoder based on unsupervised learning was applied as an outlier detection to overcome this problem. For the experiment, two experiments were designed: one is univariate learning, in which only SST data was used among the observation data of Deokjeok Island and the other is multivariate learning, in which SST, air temperature, wind direction, wind speed, air pressure, and humidity were used. Period of data is 25 years from 1996 to 2020, and a pre-processing considering the characteristics of ocean data was applied to the data. An outlier detection of actual SST data was tried with a learned univariate and multivariate autoencoder. We tried to detect outliers in real SST data using trained univariate and multivariate autoencoders. To compare model performance, various outlier detection methods were applied to synthetic data with artificially inserted errors. As a result of quantitatively evaluating the performance of these methods, the multivariate/univariate accuracy was about 96%/91%, respectively, indicating that the multivariate autoencoder had better outlier detection performance. Outlier detection using an unsupervised learning-based autoencoder is expected to be used in various ways in that it can reduce subjective classification errors and cost and time required for data labeling.
1. 서론해양 관측 자료는 해양 예측(Arribas et al., 2011; Smith et al., 2007), 해양의 변동성 이해(Palmer et al., 2007; Levitus et al., 2012; Boyer et al., 2005; Durack and Wiffels, 2010), 해양 재분석에 필요한 입력자료 생성(Balmaseda et al., 2008) 등 많은 연구에서 응용된다(Good et al., 2013). 최근 관측 기술의 발달로 다양한 해양 관측 자료가 수집되고 있지만 미흡한 장비 관리와 불안정한 전원 공급, 모니터링 센서의 오작동으로 인해 이상 자료가 자주 발생한다(Cho et al., 2013). 이상 자료를 사용하면 해양 분석/예측 시스템 전체에 영향을 미칠 가능성이 높다(Cummings, 2011). 따라서 이상 자료가 분석에 영향을 미치지 않도록 높은 수준의 이상 자료 탐지 기법을 거친 해양 자료의 사용이 필요하다(Good et al., 2013).
전통 통계 기법을 활용한 해양 이상 자료에 대한 탐지 연구는 이전부터 활발하게 이루어지고 있다. Ingleby and Huddleston (2007)은 베이지안 확률 이론을 사용하여 해양 수온의 이상 자료를 탐지하였다. Doong et al.(2007)은 연안 해역 관측 자료에 자동 회귀와 Markov 기법 등의 통계 기법을 이용하여 이상 자료를 탐지하였다. Cho et al.(2013)은 연안 수온 자료의 단기적 변동성에 z-scoring 기법을 이용하여 이상 자료를 탐지하였다. Array for Real-time Geostrophic Oceanography (ARGO) 프로그램은 과거 자료의 통계적 특성을 기반으로 하는 기법 등을 이용하여 엄격한 이상 자료 탐지를 시행하고 있다(Wong et al., 2003; Jingang et al., 2017). 그러나 이러한 전통 통계 방식의 이상 탐지 기법들은 비선형 고차원 자료에 부적절하다는 한계점이 있다(Giannoni et al., 2018; Yin et al., 2020). 이를 해결하기 위하여 최근에는 인공지능을 이용한 이상 탐지 방법에 대한 연구가 많은 관심을 받고 있다.
Rumelhart et al.(1986)에 의해 Artificial Neural Network (ANN)이 재발견된 이후로 최적화를 거쳐 Deep Belief Networks(DBN)와 Convolutional Neural Networks(CNN), Recurrent Neural Networks(RNN), Long Short-Term Memory(LSTM) 등의 여러가지 인공지능 기법이 개발되었으며 이를 이용한 이상 자료 탐지 연구도 활발하게 진행되고 있다(Williams and Gu, 2002; Kim and Cho, 2018; Charte et al., 2018). 이러한 인공지능 기반 이상 탐지 기법은 모든 학습자료에 이상 또는 정상으로 판별하는 분류(라벨) 정보가 필요한 지도학습이다. 라벨 정보의 생성은 해양 전문가의 주관적 판단에 의한 수작업으로 진행해야 한다는 점에서 시간적으로나 비용적으로 어려움이 있다. 따라서 라벨링 작업 없이 학습이 가능한 비지도학습 기반의 이상 자료 탐지 방법이 필요하다.
본 연구에서는 비지도학습을 위하여 오토인코더를 활용한 이상 탐지 기법 및 해양-기상 자료의 특성을 고려한 전처리 방법을 활용하여 기상청에서 제공하는 덕적도 부이의 연안 해양 표층 수온 시계열 자료의 이상 탐지를 시도하였다. 또한 오토인코더의 성능 및 단변수와 다변수 오토인코더의 성능을 비교하였다.
2. 자료본 연구에서 사용된 자료는 한국 기상청(Korea Meteorological Administration, KMA)의 기상 자료 개방 포털에서 제공하는 1996년부터 2020년까지 25년 기간에 대한 덕적도(36.58°N, 129.40°E) 해양 기상 부이의 표층 수온과 표층 기온, 풍향, 풍속, 습도, 기압 등의 자료이다(Fig. 1). 제공받은 모든 자료를 사용하여 표층 수온에 대한 이상 탐지를 수행하였으며, 표층 수온만을 사용한 단변수 이상 탐지 기법과 모든 자료를 사용한 다변수 이상 탐지 기법을 구현하였다. Fig. 1의 표층 수온 그림에서 붉은색 직사각형으로 표시된 기간을 확대하여 Fig. 2에 표시하였다. Fig. 2는 2000년도의 표층 수온 자료를 나타내며 이상 자료와 결측 자료가 존재한다. 이는 분석/예측 결과의 신뢰성에 영향을 미치므로 이상 자료와 결측 자료를 적절하게 처리하여야 한다(Cho et al., 2013).
본 연구에서는 이상 자료 탐지에 중점을 둔 연구를 진행하였으며 비교적 단기간의 시계열 자료에 대한 이상 자료 탐지를 하고자 하였다. 구체적으로는 해양 자료의 일주기를 고려 하여 24시간의 크기와 간격(stride)의 time window로 나누어 단기간 이상 탐지 모델을 학습시키고자 하였다. 학습에 결측 자료가 미치는 악영향을 고려하여 동시간대 6개 변수의 time window에서 결측 자료가 존재할 경우 해당 시간대의 자료를 제외하였다.
기상청에서는 기본적으로 풍향을 16방위로 측정하고 있으며, 0~360°로 환산된다. 시계방향으로 북쪽은 0° 또는 360°와 동쪽으로는 90°, 서쪽으로는 270°가 되며 이는 풍향 시계열 자료의 연속성을 해치게 되어(예, 360° ~1°) 인공지능 모델 학습에 악영향을 주기 때문에 풍향과 풍속 자료를 직교좌표계 상의 벡터로 변환하였다. 풍향과 풍속 자료를 직교 좌표계 상의 벡터로 변환하는 식은 다음과 같다.
여기서 s와 deg는 각각 풍속과 풍향을 나타낸다.
본 연구에서는 해양 기상부이에서 제공하는 6개의 변수(표층 수온과 표층 기온, 풍향, 풍속, 습도, 기압)를 이용하여 이상 탐지를 진행하고자 하였다. 인공지능 이상 탐지 기법의 효율적인 학습을 위해선 변수들 간의 평균과 표준편차가 비슷한 수준이어야 하므로 전체 학습 자료에 최대·최소 정규화를 하였으며 공식은 다음과 같다.
전처리 과정의 마지막 단계로, 이상 탐지 기법의 학습과 검사를 위해 전체 자료를 3구간으로 나누었다. 오토인코더를 활용한 이상 탐지 기법의 높은 학습 성능을 위하여 이상 자료 및 결측 자료가 비교적 적은 2015~2020년을 학습을 위한 자료로 선정하였으며 이상 자료 및 결측 자료가 많은 1995~2003년을 평가를 위한 구간으로 선정하였고 나머지 구간을 학습유효성 검증을 위하여 사용하였다.
3. 연구 방법3.1 이상 탐지를 위한 비지도 학습 방법본 연구에서는 오토인코더 인공지능 기법을 사용하였다. 오토인코더는 입력 자료를 압축하여 특징을 추출하는 인코더 부분과 추출한 특징을 바탕으로 입력 자료를 재구성하는 디코더 부분이 연결된 형태이다(Fig. 3). 또한 오토인코더는 입력 자료와 재구성 자료(출력 자료)의 차이 최소화를 목표로 학습한다. 오토인코더의 입력층과 출력층의 크기는 입력 자료의 크기인 24이며 특징을 추출하는 잠재 공간(latent space) 의 크기는 2로 설정하였다.
학습이 완료된 오토인코더의 입력 자료 벡터와 재구성 자료 벡터의 차이를 이용하여 이상 자료를 탐지하고자 하였다. 이상 자료의 판단 기준은 다음과 같은 방식으로 산정한다.
A(x)는 입력 자료 벡터 x와 오토인코더의 출력 값인 재구성 자료 벡터 D(E(x))의 차이를 제곱하여 산정한 이상 점수이다 . 학습이 완료된 오토인코더는 이상 자료를 입력 받았을 때이상 점수가 크게 나타난다. 식(3)에서 산정된 이상 점수를 이용하여 정상 자료와 이상 자료를 판별할 수 있는 적절한 임계치를 정하여 이상 자료를 탐지하고자 하였다.
3.2 단변수 오토인코더본 연구에서는 먼저 표층 수온만을 학습하여 표층 수온에 대하여 이상 탐지를 하는 단변수 오토인코더를 구현하였으며그 식은 다음과 같다.
인코더 E(x)를 활용하여 24 크기의 입력 자료 벡터 xt(t = 1, ..., T)를 2크기의 벡터로 압축시킨 뒤 활성화 함수(activation function) F(x)를 거쳐 잠재 벡터(latent vector) zt(x)로 표현 한다(식(4a)와 식(4b)). 인코더의 Winp는 24-2의 가중치 행렬이며, binp는 편향 벡터이다. 잠재 벡터 zt(x)는 디코더 D(x)와 활성화함수 F(x)를 거쳐 24 크기의 재생성 벡터 Rt(x)로 매핑된다(식(4c)와 식(4d)). 디코더의 Wout는 2-24의 가중치 행렬이며, bout은 편향 벡터이다. 위의 과정을 T번째 학습 자료까지 거친다.
식(4b)와 식(4d)에서 사용된 활성화 함수 F(x)는 시그모이드(Sigmoid) 함수이며 S자와 유사한 완만한 시그모이드 곡선의 형태를 가진다. 시그모이드 함수는 모든 실수 입력값을 0 보다 크고 1보다 작은 미분 가능한 수로 변환하는 특징을 가지므로 이상 탐지 기법의 학습과정에서 의미 있는 자료를 강조하기 위하여 사용된다. 식은 다음과 같다.
위의 과정에서 사용된 인코더와 디코더의 매개변수 θinp = {Winp, binp}와 θout = {Wout, bout}는 오토인코더의 입력 자료와 재구성 자료의 차이를 최소화하도록 최적화한다. 본 연구에서는 아담 최적화 알고리즘(Adam optimizer)을 반복 사용하여 오토인코더의 최적의 가중치를 구하였으며, 식은 다음과 같다.
여기서 L(x, R(x))은 Mean Squared Error 손실함수이며 식은 다음과 같다.
오토인코더는 입력 자료와 잠재 자료, 재구성 자료 등을 한정된 컴퓨터 메모리 자원에 옮겨 학습을 진행한다. 입력 자료의 크기가 너무 커질 경우 한번 학습하는데 오랜 시간이 걸리며 입력 자료의 크기가 너무 작아질 경우 학습 과정에서 자료 전체의 경향을 반영하기가 힘들다. 본 연구에서는 오토인코더 학습에 미니배치(mini batch) 최적화를 적용하여 학습의 효율 성을 향상시켰으며 미니배치의 크기는 256으로 설정하였다.
3.3 다변수 오토인코더표층 기온과 풍향, 풍속, 습도, 기압의 입력 변수와 출력 변수인 표층 수온 간의 상관관계를 학습하여 단변수 오토인코더의 표층 수온에 대한 이상 탐지 성능을 향상시킨 다변수 오토인코더를 구현하였다. 구체적으로 기존 24-2-24의 단변수 오토인코더의 앞부분에 다변수와 단변수간의 상관관계를 추출하는 144-24의 인코더 층을 추가하여 144-24-2-24 크기의 다변수 오토인코더를 구현하였다.
본 연구에서 사용한 다변수 오토인코더의 공식은 다음과 같다.
[Section 3.2]의 단층으로 설계한 단변수 인코더와는 다르게 다변수 인코더는 두개의 층으로 설계하였다. 다변수 오토인 코더에서 추가된 인코더 층의 매개변수
4. 연구 결과4.1 학습 유효성 평가단변수와 다변수 오토인코더를 1e-4의 학습률(learning rate) 으로 8000 Epoch 동안 학습하여 오토인코더의 재구성 자료와 학습자료 간의 MSE 손실 함수 값을 최소화하고자 하였다. 학습이 완료된 오토인코더의 손실 함수의 값이 최소화되면 오토인코더의 학습이 유효하다고 판단된다. 오토인코더의 학습의 유효성을 판단하기 위하여 Epoch 당 학습 자료의 재구성 오차와 유효 자료의 재구성 오차와의 MSE 손실 값을 구하여 그림으로 나타내었다.
Fig. 4는 단변수(Fig. 4a)와 다변수(Fig. 4b)로 학습한 오토 인코더의 학습자료와 재구성자료 간의 MSE 손실 함수의 곡선을 나타낸다. 검은색 선은 학습 자료(2015~2020)의 손실 값을 나타내며 붉은색 선은 유효성 검사를 위한 자료(2003~ 2010)의 손실 값을 나타낸다. 그림의 x축은 Epoch를 나타내며 y축은 Epoch에서의 손실 값의 평균을 나타낸다. 단변수와 다변수의 손실 곡선 둘 다 Epoch가 진행될수록 손실 값이 0에 가까워지는 모습을 보인다. 대부분의 Epoch에서 학습 자료의 손실 값이 유효 자료의 손실 값 보다 작은 모습을 보인다. 단변수 오토인코더와는 달리 다변수 오토인코더는 손실 곡선의 학습 초반 구간에서 곡선의 기울기가 급격하게 변하는 모습을 보인다.
Fig. 4에서 Epoch가 진행될수록 손실 값의 감소 폭이 줄어드는 모습을 보인다. 단변수에서는 3000 Epoch에서 다변수에서는 2000 Epoch에서 손실 값이 거의 줄어들지 않는 모습을 보여서 충분한 학습이 되었음을 확인할 수 있다. 유효성 손실 값이 학습 손실 값을 따라가며 0에 가까워지는 모습을 보여 학습 도중 과적합 현상이 일어나지 않았음을 확인하였다. 이러한 분석을 통해 단변수와 다변수 오토인코더의 학습 과정이 유효하였다고 판단된다.
4.2 학습 결과단변수와 다변수 오토인코더의 학습 결과를 확인 및 비교하기 위해 학습 자료에 대하여 재구성 및 이상 탐지를 시도하였다. 학습이 정상적으로 된 오토인코더는 입력 자료의 특징을 유의미하게 재구성하므로 입력 자료와 재구성 자료의 차이를 제곱하여 산정한 이상 점수는 이상 자료 구간에서 높은 값을 가져야 한다. 본 실험에서는 단변수와 다변수 오토인코더의 재구성 자료와 이상 점수를 그림으로 나타내어 단변수와 다변수 오토인코더의 학습 결과를 비교하고자 하였다.
Fig. 5와 Fig. 6에서는 학습 자료 중 2000년도의 자료를 통하여 단변수와 다변수 오토인코더의 출력 자료의 재구성 학습 결과를 확인 및 비교하고자 하였다. x축은 시간을 나타내며 y축은 전처리가 끝난 표층 수온 자료를 나타낸다. Fig. 5a 와 Fig. 6a에서 검은색 선은 자료 전처리가 끝난 입력 자료 (SST)를 나타내며 붉은색 선은 학습이 완료된 오토인코더가 입력 자료를 받아 출력한 재구성한 자료를 나타낸다. 단변수 오토인코더의 재구성 자료는 하강하는 추세를 잘 따라가지 못하는 모습을 보였다(Fig. 5a). 다변수 오토인코더의 경우 표층 수온 입력 자료의 겨울철 하강하는 추세를 재구성 자료가잘 따라가고 있음을 보였다(Fig. 6a). Fig. 5b와 Fig. 6b에서 검은색 선은 입력 자료와 재구성 자료의 차이를 제곱하여 산정한 이상 점수를 나타낸다. 붉은색 직선은 이상 점수를 활용하여 이상 자료를 판단하기 위해 설정한 임계값이며 실험을 통하여 적절한 값(0.003)을 설정하였다. 단변수 오토인코더의 경우 2~4월과 6월에서 임계치를 넘는 이상 점수를 보이며 다변수 오토인코더의 경우 6월에서만 임계치를 넘는 이상 점수를 보인다.
Fig. 5a의 2~4월에서 표층 수온 입력 자료의 겨울철 하강 추세를 단변수 오토인코더의 출력값인 재구성 자료가 따라가지 못함을 보였으나 Fig. 6a에서는 동기간의 다변수 오토인코더의 재구성 자료는 비교적 하강 추세를 따라가는 모습을 보였다. 마찬가지로 단변수 오토인코더의 2~4월 이상점수는 임계값을 넘어 이상 자료로 오판하는 구간이 있으나 Fig. 6b에서는 정상 자료로 판단하였다. 이를 통해 다변수 오토인코더가 입력 변수 간의 상관관계를 추가로 학습하여 비선형 변동성을 좀 더 의미있게 추정하는 것을 확인하였다.
Fig. 5b와 Fig. 6b에서 산정된 단변수와 다변수 오토인코더의 이상 점수를 이용하여 표층 수온에 대한 이상 탐지를 시행하였으며 탐지 결과를 Fig. 7와 Fig. 8에 나타내었다. 이를 통해 단변수와 다변수 오토인코더의 이상 자료 탐지 성능을 비교하였다.
4.3 정량 평가학습이 완료된 단변수와 다변수 오토인코더를 수치적으로 비교분석하기 위하여 단변수와 다변수 오토인코더를 포함한 여러 이상 탐지 기법에 대한 정량 평가를 실시하였다. 오토인코더를 활용한 이상 탐지 기법의 정량 평가를 위해선 분류 정보가 있는 자료가 필요하다. 본 실험에서는 Test 자료의 약 40% 비율에 인위적으로 오차를 삽입하여 정량 평가를 위한 합성 자료를 생성하였다. 합성 자료에 대하여 오차가 삽입된 구간을 이상 자료로 분류한 라벨 자료를 생성하였다. 생성된 합성자료는 학습자료와 같은 전처리 방식을 거친다.
단변수와 다변수 오토인코더에 실시한 정량평가를 통하여 전체 결과 중 실제 정상 자료와 실제 이상 자료를 제대로 판단하는 비율을 나타내는 정확도(Accuracy)와 이상 자료로 판단된 자료 중 실제 이상 자료의 비율을 나타내는 재현율 (Recall)을 보고자 하였다. 식은 다음과 같다.
TP(True Positive)는 이상 자료로 판별된 실제 이상 자료의 수이며 TN(True Negative)는 정상 자료로 판별된 실제 정상 자료의 수이다. 반면 FP(False Positive)는 이상 자료로 판단된실제 정상 자료의 수를 나타내며 FN(False Negative)는 정상 자료로 판별된 이상 자료의 수를 나타낸다.
본 연구에서는 파이썬의 이상 탐지 패키지인 ADTK(Anomaly Detection Tool Kit, https://arundo-adtk.readthedocs-hosted.com)의 SeasonalAD를 이용하여 제안 기법인 오토인코더와의 이상 탐지 성능을 비교하고자 하였다. ADTK SeasonalAD는시계열을 장기성분(계절성)과 단기성분으로 나눈 뒤 단기성분의 편차를 구하여 이상 자료를 탐지하는 이상 탐지 모델이다.
[Section 4.2] 학습결과에선 임의의 이상 점수에 대한 임계값으로 이상 자료를 탐지한 다변수 오토인코더가 단변수 보다 더 나은 이상 탐지 성능을 보였다. 하지만 오토인코더를 이용한 이상 탐지 기법은 이상 점수에 대한 임계값에 따라서 이상 탐지 결과가 달라진다(Fig. 5b와 Fig. 6b). 따라서 단변수와 다변수 오토인코더에 실시한 정량 평가의 정확도 지표를 이용하여 모든 임계값에서 다변수 오토인코더 이상탐지 성능이 단변수 보다 좋음을 확인하고자 하였다.
Fig. 9는 임계값에 따른 정확도 곡선을 나타낸다. x축은 임계치이며 y축은 단변수와 다변수 오토인코더 이상 탐지의 정확도를 나타낸다. 검은색 곡선은 단변수 오토인코더의 임계값에 따른 정확도이며 붉은색 선은 다변수 오토인코더의 임계값에 따른 정확도를 나타낸다. 또한 이상 탐지 기법별 정확도 비교를 위하여 ADTK SeasonalAD의 정확도를 푸른색 직선으로 나타내었다. 모든 임계값에서 다변수 오토인코더가 단변수보다 더 높은 정확도를 보였다. 단변수/다변수 오토인 코더의 임계값이 0.0052/0.0026일 때 약 91%/96%의 최대 정확도를 보였고, 비교를 위한 이상 탐지 기법 ADTK SeasonalAD의 정확도는 약 77%를 보였다. 해당 정확도의 결과는 Table 1에 표시하였다.
Table 1의 Accuracy에서 단변수와 다변수 오토인코더 모두 정상 자료 비율(약 60%)를 넘는 정확도를 보였다. 이는 단변수와 다변수 오토인코더의 이상 자료 탐지 성능이 유효함을보여준다. 그리고 Fig. 9에서 다변수 오토인코더가 모든 임계값에서 단변수 오토인코더보다 높은 정확도를 보였다. 이를 통해 임계값에 관계없이 다변수 오토인코더의 이상 탐지 성능이 항상 단변수보다 뛰어남을 확인하였으며 최대 정확도의 차이는 약 5%를 보여 유의미한 최대 성능 차이를 보였다고 판단된다. 또한 Table 1의 Threshold에서 단변수/다변수의 최적의 이상 점수 임계값은 각각 0.0052/0.0026임을 확인하였다.
오토인코더를 활용한 이상 탐지 기법의 정확도 평가를 통하여 임계값에 관계없이 항상 다변수 오토인코더의 이상 탐지 성능이 단변수 오토인코더보다 더 나음을 확인하였다. 다음은 이상 탐지 기법의 정량 평가 결과를 구체적으로 확인하여 다변수 오토인코더의 어느 부분이 단변수 오토인코더와 차이가 있는지를 확인하였다.
Table 2는 단변수와 다변수 오토인코더의 이상 탐지 정량 평가를 혼동행렬로 나타낸 것이다. 실제 정상 자료에 대한 이상 탐지 정량 평가 결과는 단변수와 다변수 오토인코더가 서로 같았다. 실제 이상 자료에 대한 정량 평가 결과에 대하여 이상 자료를 정상 자료로 오판하는 수가 단변수는 1902건, 다변수는 471건이었다. 위의 결과를 통하여 재현율을 구하였으며 단변수 오토인코더의 재현율은 0.8371, 다변수의 재현율은 0.9597을 보였다.
Table 2에서 단변수와 다변수 오토인코더의 이상 탐지 혼동 행렬에서 실제 이상 자료를 정상 자료로 오판하는 수가 1902건에서 471건으로 1431건 줄어들었다. 이상 탐지의 분야에서 정상 자료를 이상 자료로 판단하는 오류보다 이상 자료를 정상 자료로 판단하는 오류가 더 치명적이다. 재현율 또한 0.8371에서 0.9597으로 12% 이상 향상되었다. 단변수와 다변수 오토인코더에 실시한 정량 평가 결과의 혼동 행렬을 통하여 다변수 오토인코더의 이상 탐지 성능이 단변수보다 더 나은 이유는 다변수와 단변수 간의 비선형적 상관관계를 추가로 학습함으로써 이상 자료를 정상 자료로 판단하는 오류가 눈에 띄게 감소하였기 때문인 것으로 판단된다.
4.4 원시 관측 자료에 대한 이상 탐지 결과
[Section 2] 자료 전처리과정에서 결측값이 학습에 결측 자료가 미치는 악영향을 고려하여 동시간대 6개 변수의 time window에서 결측 자료가 존재할 경우 해당 시간대의 자료를 제외하였다. 이러한 자료는 이상 탐지 기법의 학습과 정량평가에는 유용하나 실제 자료에 대한 이상 탐지 유효성 확인에는 사용될 수 없다. 본 실험에서는 학습이 완료된 단변수와 다변수 오토인코더가 해양예보 등의 현실 적용에 유용한지 판단하기 위하여 제외된 자료가 없는 원시 자료에 대한 이상 탐지를 실시하였다. 또한 원시 자료에 적용된 단변수와 다변수 오토인코더의 이상 탐지 성능을 비교하였다. 학습이 완료된 오토인코더를 활용한 이상 자료 탐지를 위해 결측 자료에 해당 변수의 최대값을 인위적으로 삽입함으로써 전체 구간을 결측 자료가 없는 시계열 자료로 보완하여 이상 탐지를 시도하였다. 이상 탐지 완료 후에는 인위적으로 삽입된 최대값을 삭제하였다.
5. 토의본 연구에서는 비지도-지도학습이 혼합된 준지도학습의 초기 단계 연구인 비지도학습을 수행하였다. 이번의 오토인코더를 통한 비지도학습 기반의 이상 탐지 연구를 통하여 향후 지도학습을 위한 자료생산이 가능하다고 판단된다. 이를 통해 추후에는 준지도학습 기반의 이상 탐지 기법을 구축 및 활용하여 이상 자료 탐지 기법의 성능 향상 연구를 수행할 예정이다.
Cho et al.(2013) 등은 표층 수온 자료에서 장기성분을 제외하여 추출된 잔차성분을 이용하여 이상 자료를 판단하였다. 이처럼 뚜렷한 연변화 양상을 보이는 시계열 자료에서의 잔차성분을 이용한 이상 자료 판단 기법은 좋은 성능을 보일 수있다. 반면, 본 연구에서는 돌발적인 이벤트(태풍, 해일, 폭풍등)를 포함하는 관측 자료에 대하여 이상 자료를 탐지하고자 하였다. 잔차를 이용한 학습은 이러한 돌발적인 이벤트를 충분히 학습할 수 없다고 판단되었기 때문에 잔차를 이용한 이상 탐지 기법에 대해서는 연구 검토가 수행되지 않았다. 추후 연구에서는 잔차를 이용한 AI 이상 탐지 기법에 대하여 구체적인 비교 및 검증 연구를 수행할 예정이다.
인코더의 작업 과정 중 마지막 단계에서 시그모이드 활성화 함수를 추가하였을 때 다변수 오토인코더의 정확도가 단변수 오토인코더 보다 약 5% 높아짐을 확인하였다. 단변수 오토인코더의 정확도는 시그모이드 활성화 함수 추가에도 성능 향상이 미미하였다. 이는 시그모이드 활성화 함수의 추가로 인하여 다변수 오토인코더의 특징을 추출하는 기능이 개선되었기 때문이라고 판단된다.
본 연구에서는 다수의 변수를 이용하여 표층 수온에 대한 이상 자료 탐지를 수행하였다. 각 변수의 이상 자료 탐지 성능에 대한 기여도 평가 연구가 필요하나 이번 연구에서는 입력층에 들어가는 변수들의 기여도와 이에 대한 과학적 분석은 다루지 않았다. 추후 연구에서는 설명가능한 인공지능 (eXplainable AI, XAI)이나 가중치 분포 분석 등을 통하여 변수들의 기여도 평가 및 과학적 분석을 수행할 예정이다.
24시간 이하에서 값이 20%가량 변동하는 이상 자료 구간에서 일부 자료를 정상 자료로 오판하였다. 이처럼 특정 이상 자료 유형에 대한 오판은 해당 유형을 학습시켜 해결될 수 있다고 판단된다. 본 연구에서는 명확한 정상 자료에 다양한 유형의 이상 자료를 자연스럽게 섞어 넣음으로써 특정 유형에 대한 이상 탐지 성능을 향상시키고자 하였으나 다양한 유형의 이상 자료를 인공적으로 만들어 내는 것에 어려움이 있었다. 추후에는 정상 자료에 자연스럽게 구성된 유형별 이상 자료와 라벨 데이터를 생성하는 연구를 진행할 예정이다. 이를 통해 하나의 모델만으로도 대부분의 이상 자료 유형을 학습 및 탐지할 수 있을 것으로 판단된다.
6. 결론본 연구에서는 연안 해양 표층 수온 시계열자료에서 이상 자료 탐지를 하기 위한 비지도학습 기반 오토인코더 적용기법을 제시하였다. 제시한 기법은 학습에 필요한 모든 자료마다 수작업을 통해 자료마다 라벨을 지정해야 하는 기존의 지도학습 AI기법에 비해 라벨작업이 필요 없다는 점에서 시간과 비용이 적은 장점이 있다. 오토인코더의 첫 단계에서 여러 변수들과 표층 수온 간의 상관관계를 학습하는 층을 추가하였고 이를 통해 단변수와 다변수의 이상 탐지 성능을 비교 하였다.
모델의 이상 자료 탐지 성능을 비교하기 위해 인위적 오차를 삽입한 합성 자료에 단변수와 다변수 오토인코더를 포함한 여러 이상 탐지 기법을 이용하여 정량 평가를 하였다. 단변수 오토인코더의 이상 자료 탐지의 정확도/재현율은 각각 약 91%/84%인 반면 다변수 오토인코더는 각각 약 96%/96%로써 다변수 오토인코더가 더 나은 성능을 보였다. 이를 통해 다양한 종류의 자료를 학습함으로써 각 관측자료가 내포하고 있는 고유한 물리적 특징으로부터 벗어난 자료에 대한 탐지 성능을 향상시킬 수 있음을 확인하였다.
단변수와 다변수로 학습한 오토인코더를 적용하여 덕적도의 1996~2020년간 연안 해양 자료에 대한 이상 탐지를 시도하였으며 다변수 오토인코더가 단변수 오토인코더보다 정상 자료를 이상자료로 오판하는 비율이 적다는 점에서 더 나은 이상 탐지 결과를 보였다. 실시간으로 수집되는 자료에 대한즉각적인 오차 여부 판단은 향후 해양예보 등의 실시간 연구에 있어서 매우 중요한 역할을 차지할 것으로 기대된다.
오토인코더를 이용한 비지도학습 기반 이상 탐지 기법은 주관적 판단에 의한 오류와 자료 라벨링에 필요한 시간과 비용을 줄일 수 있다는 점에서 다양하게 활용될 것으로 판단된다.
감사의 글이 논문은 2021년 해양수산부 재원으로 해양수산과학기술진흥원의 지원을 받아 시행된 연구임(해양수치모델링과 지능정보기술을 활용한 해양예측 정확도 향상 연구). 이 논문은 2021년도 정부(과학기술정보통신부)의 재원으로 정보통신기획평가원의 지원을 받아 수행된 연구임(2020-0-01389, 인공지능융합연구센터지원(인하대학교)).
Fig. 1.Ocean-Atmosphere data from Deokjeok buoy. Attributes shown: Sea Surface Temperature (SST), Surface Air Temperature (SAT), Wind Direction (Dir.), Wind Speed (Speed), Humidity (Hum.) and Air Pressure (Pres.). Ocean data contain many missing values and outliers, and the red rectangle indicates time series zoomed in Fig. 2. 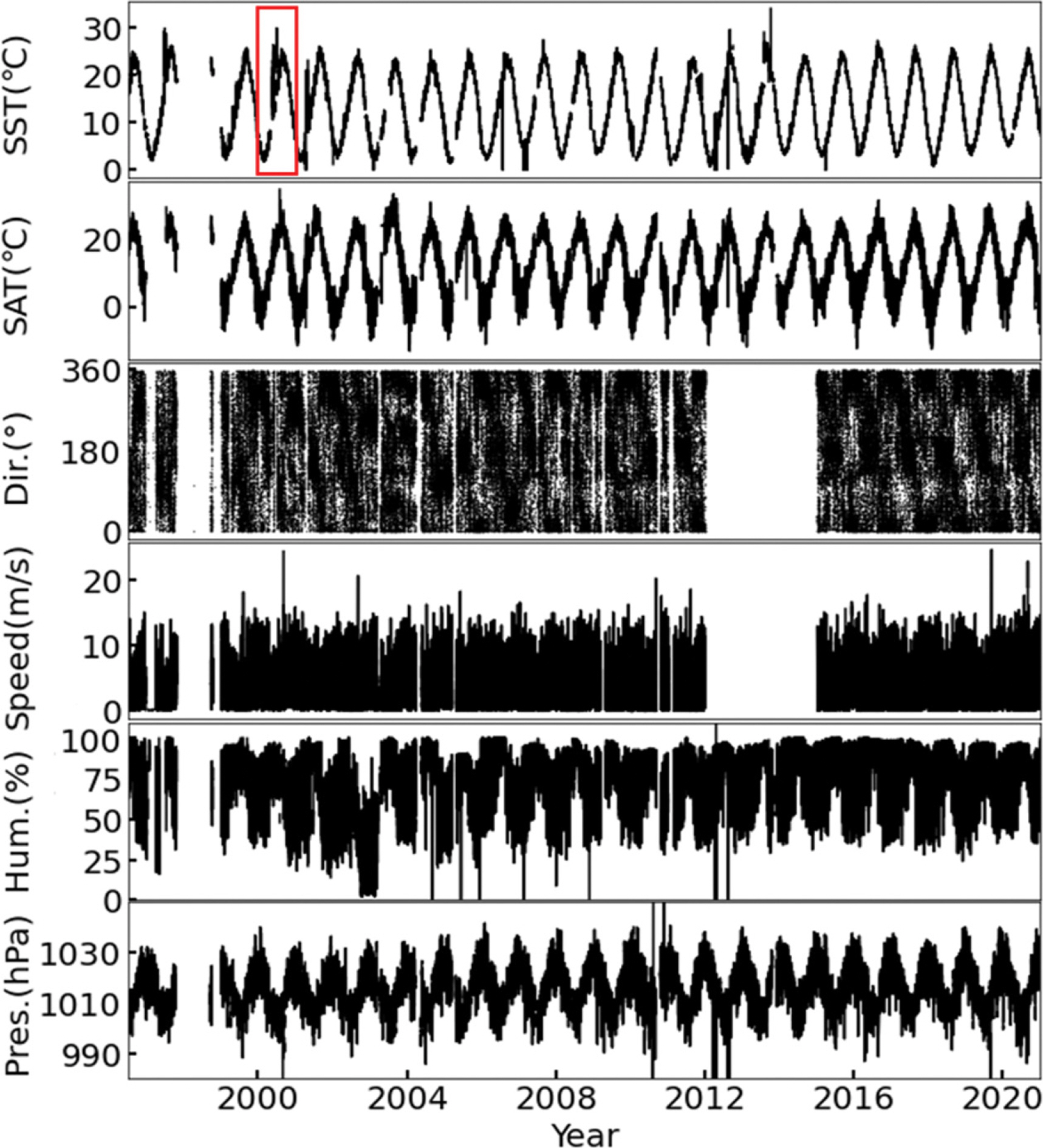
Fig. 2.Zoomed parts of time series marked by the red rectangle in Fig. 1. Black line indicates observation SST values, red dashed rectangle indicates the location of outlier of time series which has significant deviation from normal and blue dashed rectangle indicates the location of missing data. 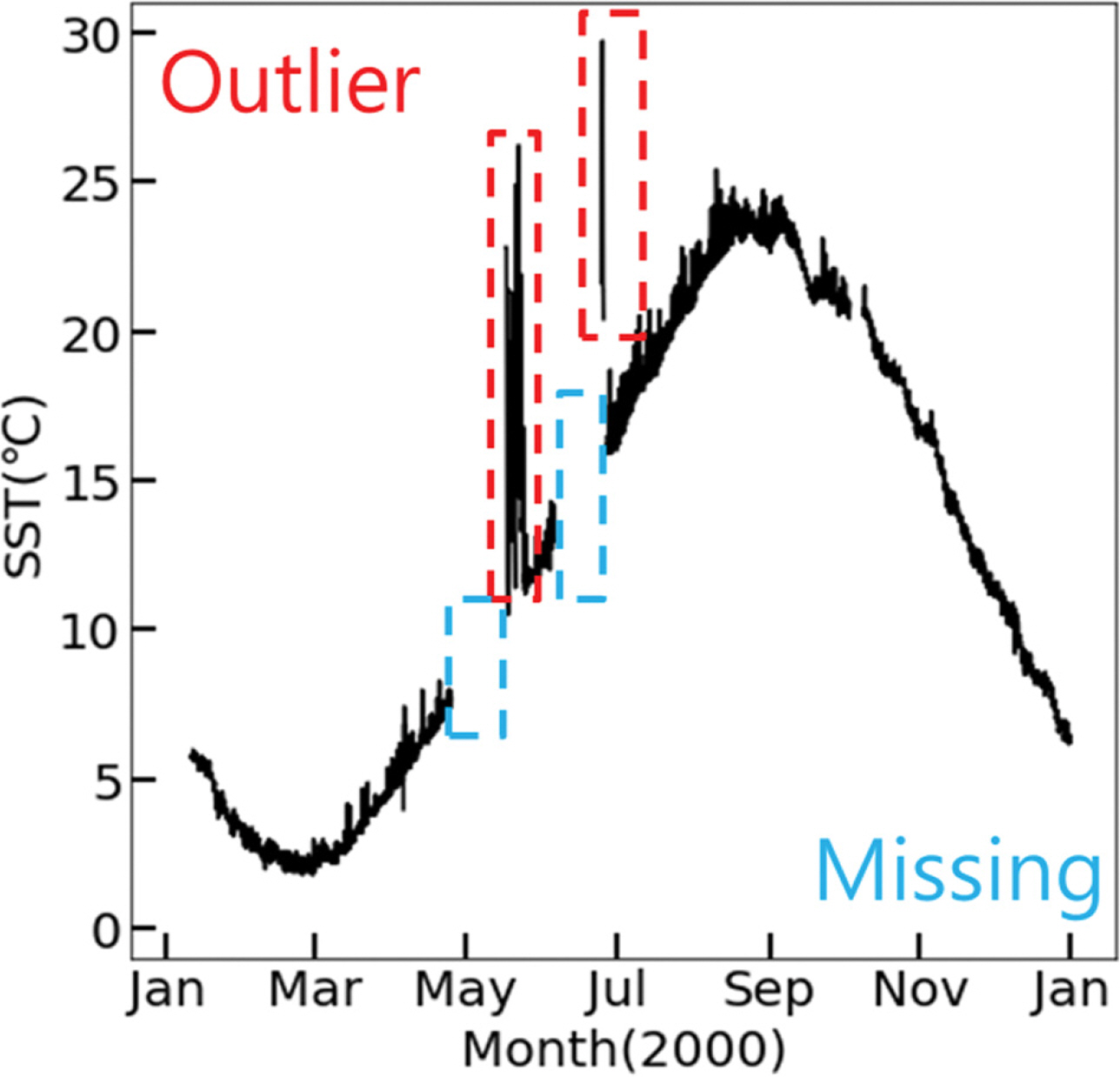
Fig. 3.The architecture of Autoencoder. From the input data (x), it is compressed through the encoder (E) and features are extracted. The input data is reconstructed through the decoder (D) with the extracted features. 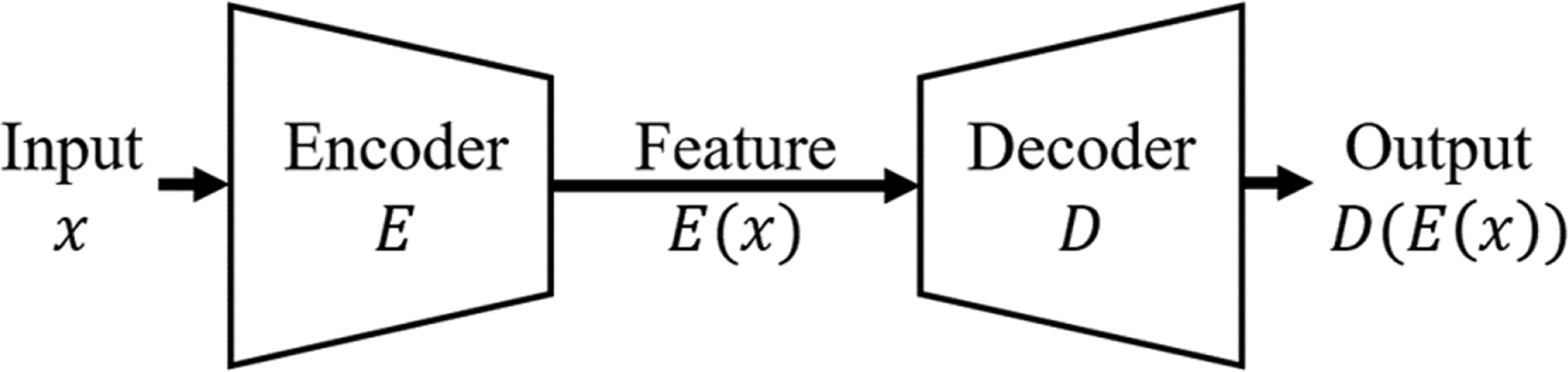
Fig. 4.The loss per epoch curve on Autoencoder training and validation step. (a) The loss curve in training step of Autoencoder trained by uni-variate. Red line indicates training loss and black line indicates validation loss. (b) The loss curve in training step of Autoencoder trained by multi-variate. Red line indicates training loss and black line indicates validation loss. 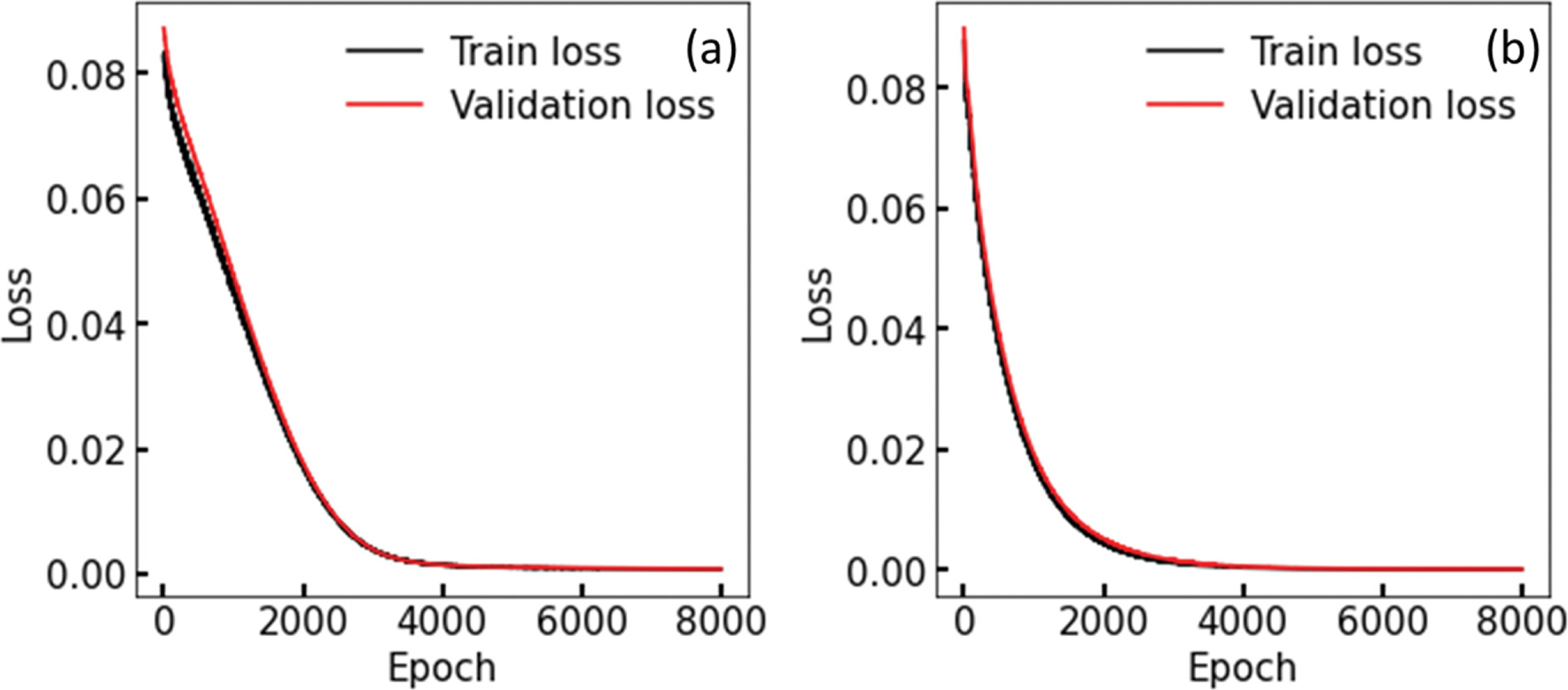
Fig. 5.Results of Autoencoder trained by uni-variate. (a) Black line indicates input SST value and red line indicates the reconstructed SST values computed by the Autoencoder. (b) Black line indicates outlier score computed by the Autoencoder. The red horizontal line is the threshold for detecting outlier. 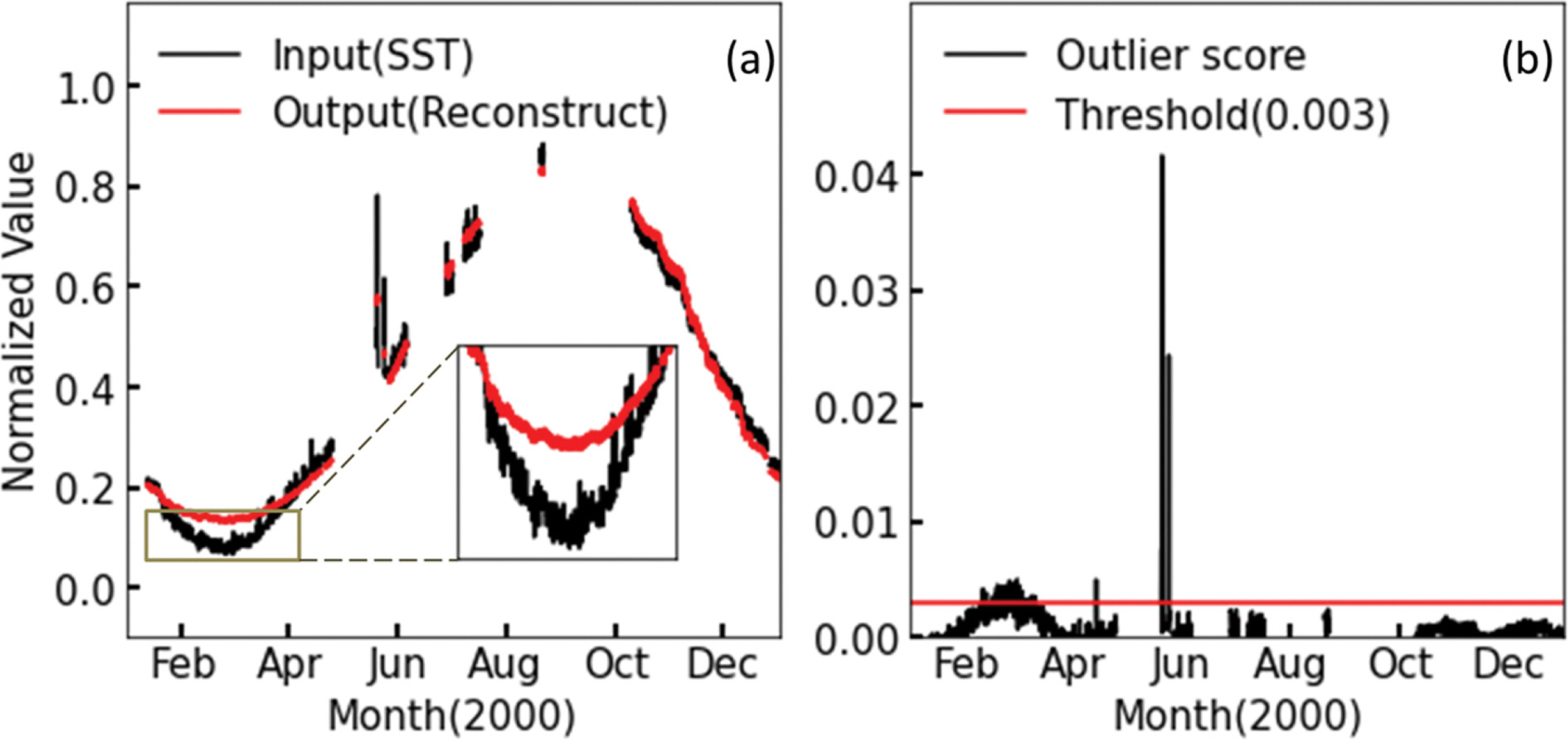
Fig. 6.Results of Autoencoder trained by multi-variate. (a) Black line indicates input SST value and red line indicates reconstructed SST values computed by the Autoencoder. (b) Black line indicates Outlier score computed by the Autoencoder. The red horizontal line is the threshold for detecting outlier. 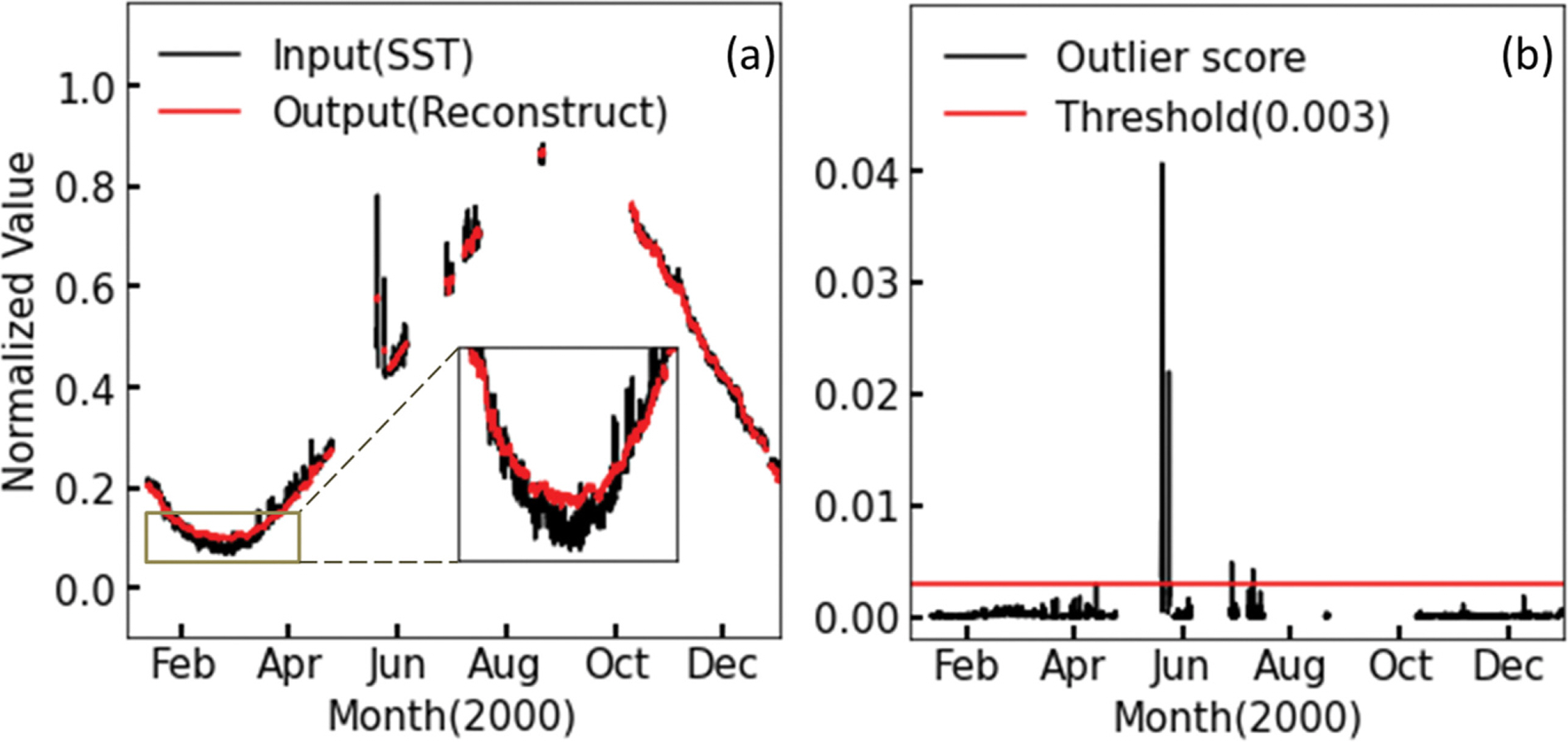
Fig. 7.Detected outliers of SST by the Autoencoder trained by uni-variate. Observation SST values are indicated by black line and outliers are indicated by red line. 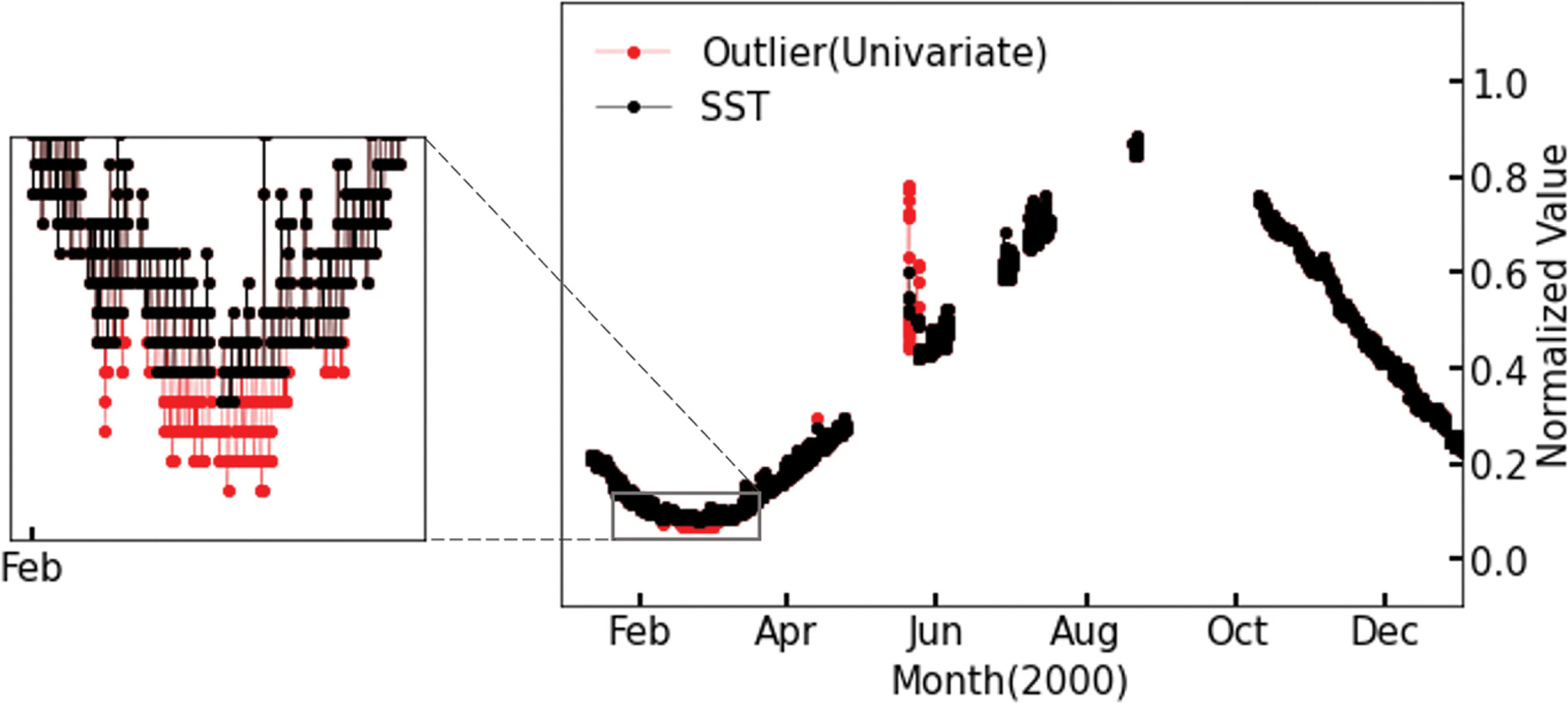
Fig. 8.Detected outliers of SST by the Autoencoder trained by multi-variate. Observation SST values are indicated by black line and outliers are indicated by red line. 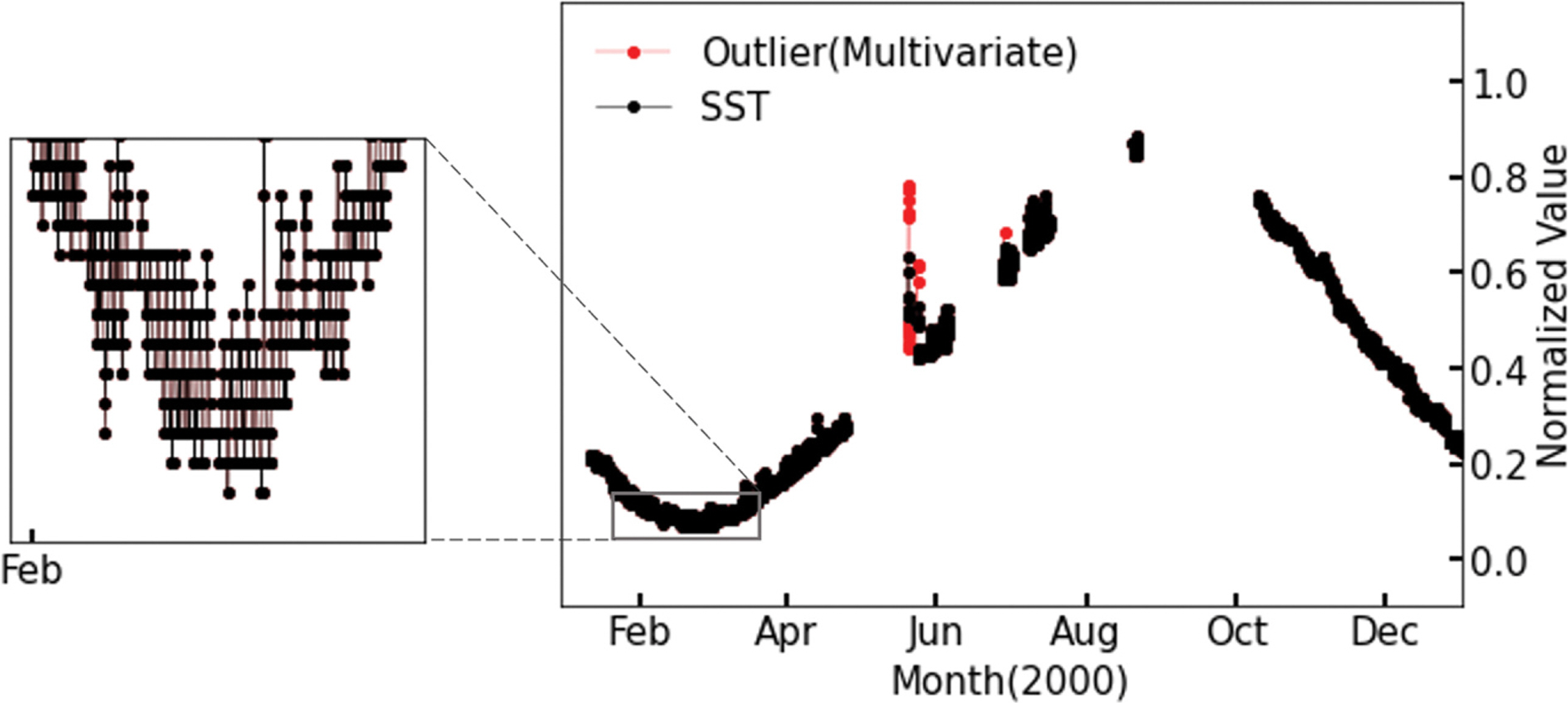
Fig. 9.Results of quantitative evaluation. The black curve indicates the uni-variate Autoencoder’s accuracy for threshold. The red curve indicates the multi-variate Autoencoder’s accuracy for threshold. The blue horizon line indicates accuracy of ADTK SeasonalAD. 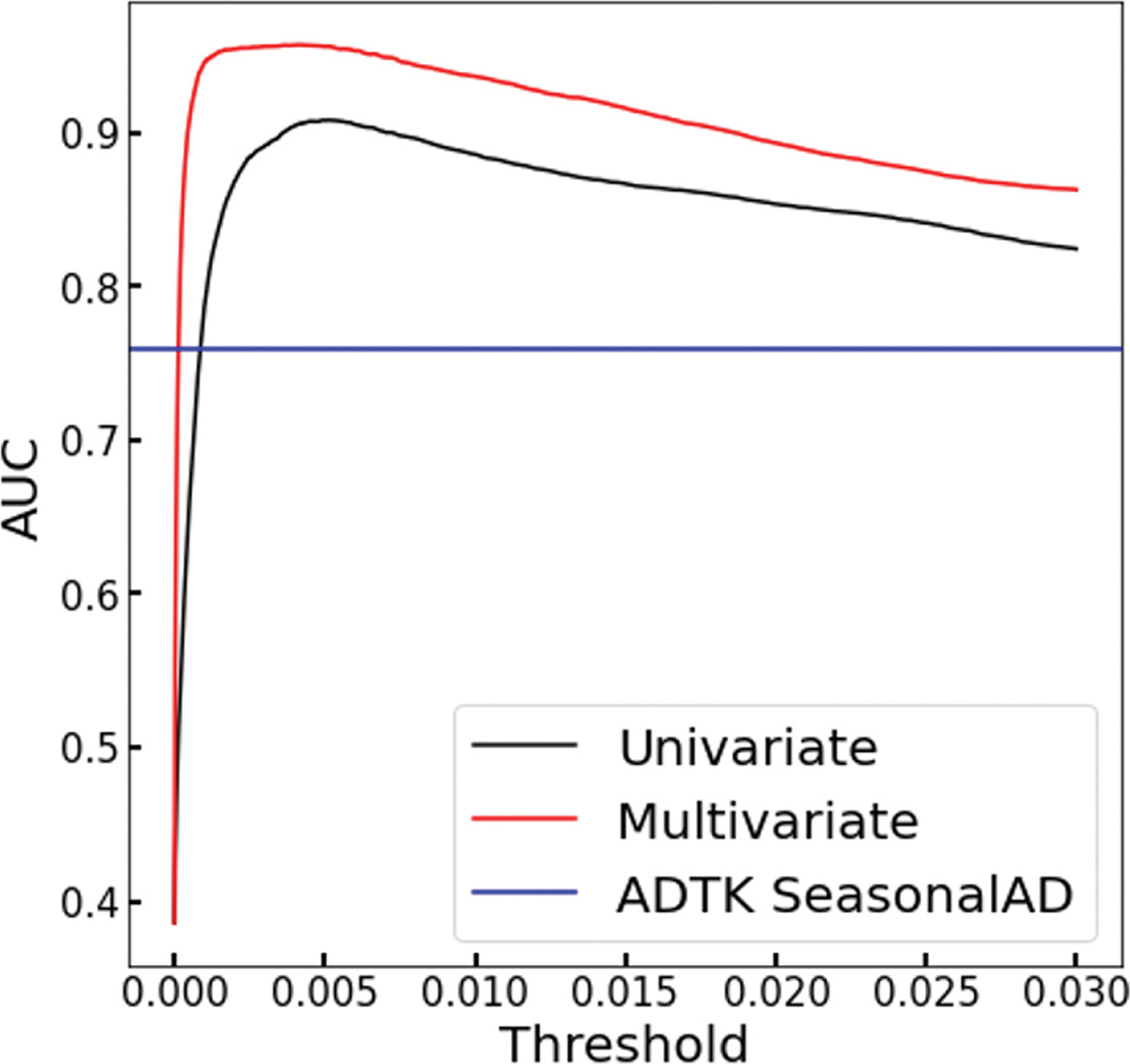
Fig. 10.Comparison of outlier detection of raw observation SST. Normal data are indicated by black line and outliers are indicated by red line. (a) In uni-variate Autoencoder, there is an error that classifies normal data as outlier. (b) In multi-variate Autoencoder, there is no error of detecting normal data as outlier. 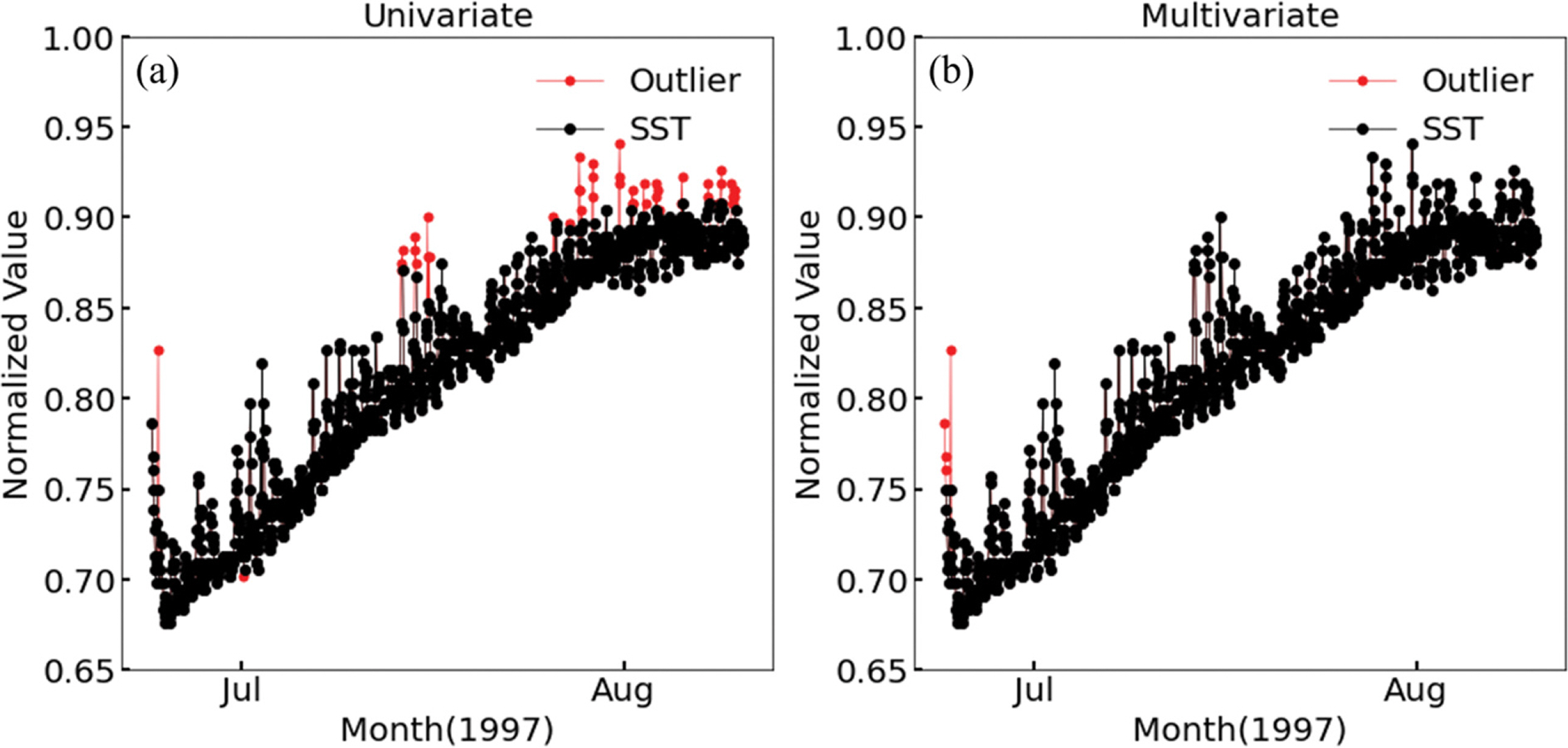
ReferencesArribas, A., Glover, M., Maidens, A., Peterson, K., Gordon, M., MacLachlan, C., Graham, R., Fereday, D., Camp, J., Scaife, A.A., Xavier, P., McLean, P., Colman, A., Cusack, S (2011). The GloSea4 ensemble prediction system for seasonal forecasting, Monthly Weather Review, 139(6):1891-1910.
Balmaseda, M.A., Vidard, A., Anderson, D.L.T (2008). The ECMWF ocean analysis system: ORA-S3, Monthly Weather Review, 136(8):3018-3034.
Boyer, TP, Levitus, S, Antonov, JI, Locarnini, RA, Garcia, HE (2005). Linear trends in salinity for the World Ocean, 1955–1998, Geophysical Research Letters, 32(1.
Charte, D., Charte, F., García, S., del Jesus, M.J., Herrera, F (2018). A practical tutorial on autoencoders for nonlinear feature fusion: Taxonomy, models, software and guidelines, Information Fusion, 44(December 2017):78-96.
Cho, H.Y., Oh, J.H., Kim, K.O., Shim, J.S (2013). Outlier detection and missing data filling methods for coastal water temperature data, Journal of Coastal Research, 165(65):1898-1903.
Cummings, JA. (2011). Ocean data quality control. In Operational oceanography in the 21st Century. p 91-121. Springer, Dordrecht.
Doong, D.J., Chen, S.H., Kao, C.C., Lee, B.C., Yeh, S.P (2007). Data quality check procedures of an operational coastal ocean monitoring network, Ocean Engineering, 34(2):234-246.
Durack, P.J., Wijffels, S.E (2010). Fifty-Year trends in global ocean salinities and their relationship to broad-scale warming, Journal of Climate, 23(16):4342-4362.
Giannoni, F, Mancini, M, Marinelli, F (2018). Anomaly Detection Models for IoT Time Series Data, arXiv preprint arXiv:1812.00890.
Good, S.A., Martin, M.J., Rayner, N.A (2013). EN4: Quality controlled ocean temperature and salinity profiles and monthly objective analyses with uncertainty estimates, Journal of Geophysical Research: Oceans, 118(12):6704-6716.
Ingleby, B, Huddleston, M (2007). Quality control of ocean temperature and salinity profiles - Historical and real-time data, Journal of Marine Systems, 65(1–4 SPEC. ISS.):158-175.
Jingang, J., Lu, S., Zhongya, F., Jiaguo, Q (2017). Outlier detection and sequence reconstruction in continuous time series of ocean observation data based on difference analysis and the Dixon criterion, Limnology and Oceanography: Methods, 15(11):916-927.
Kim, T.Y., Cho, S.B (2018). Web traffic anomaly detection using C-LSTM neural networks, Expert Systems with Applications, 106, 66-76.
Levitus, S, Antonov, JI, Boyer, TP, Baranova, OK, Garcia, HE, Locarnini, RA, Mishonov, AV, Reagan, JR, Seidov, D, Yarosh, ES, Zweng, MM (2012). World ocean heat content and thermosteric sea level change (0-2000m), 1955–2010, Geophysical Research Letters, 39(10.
Palmer, MD, Haines, K, Tett, SFB, Ansell, TJ (2007). Isolating the signal of ocean global warming, Geophysical Research Letters, 34(23.
Rumelhart, D.E., Hinton, G.E., Williams, R.J (1986). Learning Representations by Back-Propagating Errors, Nature, 323(6088):533-536.
Smith, D.M., Cusack, S., Colman, A.W., Folland, C.K., Harris, G.R., Murphy, J.M (2007). Improved surface temperature prediction for the coming decade from a Global Climate Model, Paleoceanography, 796(2007):796-799.
Williams, G, Gu, L (2002). A comparative study of RNN for Outlier Detection in Data Mining, 2002 IEEE International Conference on Data Mining, 2002, Proceedings. 709-712.
|
|
|||||||||||||||||||||||||||||||||