요약 진자형 파력발전장치(Oscillating Wave Surge Converter, OWSC)는 다양한 유형의 파랑 조건에서 효율적으로 작동해야하며 최적의 파랑에너지를 추출하도록 설계되어야 하기 때문에 OWSC의 거동과 관련된 복잡한 파랑-구조물 상호작용이 광범위한 조건에서 검토되어야 한다. OWSC의 개념 설계 및 개발단계에서 수치해석은 OWSC의 설계도구로써 좋은 대안이 될 수 있다. 본 연구에서는 기초적인 OWSC의 거동특성에 대한 검토를 목적으로 오픈소스 CFD를 이용하여 내습하는 파랑에 대한 역삼각형 플랩의 거동특성에 대한 수치해석을 수행하였다. 규칙파 내습시 주기의 변화에 따른 역삼각형 플랩 인근의 자유수면변위 및 회전각도(Flap Rotation angle)를 산정하여 구조물의 거동 특성에 대해 고찰하고, 그 결과를 수리실험과 비교·검토하여 해석성능의 타당성 및 OWSC의 관련 문제를 수치적으로 해석하기 위한 수치모델로서의 적용성능을 검증하였다. 수치해석결과는 파랑과 역삼각형 플랩의 상호작용에 의한 유체역학적 거동 특성을 양호하게 재현함을 확인하였다.
AbstractAnalyzing various wave interactions with oscillating wave surge converters (OWSC) is essential because they must be operated efficiently under a wide range of wave conditions and designed to extract optimal wave energy. In the conceptual design and development stage of OWSC, numerical analysis can be a good alternative as a design tool. This study performed a numerical analysis on the behavioral characteristics of the inverted triangle flap against the incident waves using open source CFD to examine the essential behavioral attributes of OWSC. Specifically, the behavioral characteristics of the structure were studied by calculating the free water surface displacement and the flap rotation angle near the inverted triangular flap according to the change of the period under the regular wave conditions. By comparing and examining the numerical analysis results with the hydraulic model experiments, the validity of the analysis performed and the applicability in analyzing the wave-structure interactions related to OWSC was verified. The numerical analysis result confirmed that the hydrodynamic behavior characteristic due to the interactions of the wave and the inverted triangle flap was well reproduced.
1. 서 론최근 지구온난화 등의 환경문제에 따른 신재생에너지(Renewable energy)에 대한 관심과 투자가 급속도로 증대되고 있으며, 해상풍력, 조력, 조류력, 파력 등의 발전으로 대표되는 해양에너지 중 해안선을 따라 이용 가능하고, 반복 생산이 가능한 파력발전은 유럽과 일본 등의 많은 나라에서 파력에너지 추출기술 및 파력발전 변환장치(Wave Energy Converter, 이하 WEC)에 대한 연구개발에 적극적으로 참여하고 있다. WEC의 형식에는 파동의 운동에너지를 변환하는 방식에 따라 Falcão(2010)는 가동물체형, 월파형 및 진동수주형으로 분류하기도 하지만 일반적으로 (1) Attenuator(Falnes, 2007; FEMP(Federal Energy Management Programme), 2009), (2) PA((Point Absorber) Barker et al., 2007), (3) OWSC((Oscillating Wave Surge Converter) AEA, 2006), (4) Overtopping(Powetech, 2009) 및 (5) OWC(ISSC, 2006; EPRI(Electrical Power Research Institute), 2005)으로 분류될 수 있고, 각각의 방식에 해당하는 많은 종류의 WEC들이 국내·외적으로 연구 및 개발되고 있다(Lee et al., 2014). 본 연구에서 대상으로 하는 구조물인 진자형 파력발전장치(Oscillating Wave Surge Converter, 이하 OWSC)는 해저면에 힌지로 고정된 부유식 플랩으로 구성된다. OWSC에 작용하는 파랑은 횡방향 진자운동을 유도하며, 이로부터 PTO(Power Take Off system)를 사용하여 파동의 운동에너지를 전기동력으로 변환할 수 있다. 특히, 파랑의 수립자 운동이 타원형 거동특성을 보임으로 인해 심해보다는 수평 수립자 운동이 증폭되는 해안 인근에 설치되어 입사파의 수평 수립자 운동에서 에너지를 추출하도록 설계된다(Whittaker and Folley, 2012). 지금까지 다양한 형식과 디자인으로 구성된 많은 상용 OWSC가 개발되었으며, 이 중 해저면에 힌지로 고정된 천해의 대표적인 OWSC로는 WaveRoller(Tan Loh et al., 2016), Oyster(Whittaker and Folley, 2012), bioWave(Flocard and Finnigan, 2009), EB Frond(Engineering Business Ltd., 2005), CCell(Bridgwater Court et al., 2017) 등을 들 수 있다(Tan Loh, 2018).
OWSC는 다양한 유형의 파랑 조건에서 효율적으로 작동해야하며 최적의 에너지를 추출하도록 설계되어야 하기 때문에 OWSC의 거동과 관련된 복잡한 파랑-구조물 상호작용이 광범위한 조건에서 검토되어야 한다. 따라서, OWSC의 개념설계 및 개발단계에서는 수리모형실험과 수치해석을 수행하여 다양한 파랑 환경에서의 파랑-구조물 상호작용에 대한 유체역학적 거동특성을 이해하고 성능을 높이는데 중점을 두게 된다. 수리모형실험은 OWSC의 동작과 관련된 역학을 관찰하고 이해하는데 가장 신뢰성이 담보되는 핵심적인 방법이나, 구조물의 형상 및 실험조건 변화에 대응되는 비용 및 시간이 과다하게 소요되며, 실험대상에 따라서는 왜곡축적과 같은 상사오류를 내포할 수 있고, 원형수준의 실증실험에는 많은 비용이 소요되기 때문에 수치해석을 동시에 수행함으로써 각각의 해석방법에 대한 장단점을 상호 보완할 수 있다. 즉, 수치해석의 선 수행을 통해 수리모형 대상구조물의 선정 및 실험조건 설정 등과 같은 수리모형실험 계획에 반영될 수 있고, 수리모형실험에 검증된 기초 대상 구조물을 수치해석모델에 적용하여 다양한 형상 및 실험조건 변화에 대응하여 예측실험을 통한 자료구축 및 확장이 가능하다. 특히, 수리모형실험에서는 제한적으로 제공되는 물리량의 상세한 시·공간 정보를 제공할 수 있는 큰 장점을 지니기 때문에 수치해석은 OWSC의 설계도구로써 좋은 대안이 될 수 있다.
OWSC의 수치해석에는 주파수 및 시간영역 모델 또는 경계요소법 및 포텐셜흐름 모델, SPH(Smooth Particle Hydrodynamics), CFD(Computational Fluid Dynamics)에 이르기까지 다양한 방법이 적용되고 있다. 그러나 OWSC 역학의 모델링에는 선형 이론접근방식보다 복잡한 거동으로 나타나는 유체와 구조물의 상호작용(Fluid-Structure Interaction, FSI)을 직접 시뮬레이션 할 수 있고, 이상유체(물-공기)의 경계면 추적기법과 Navier-Stokes 방정식이 적용된 CFD와 같은 비선형 수치접근방식이 더 적합하다.
CFD에 의한 OWSC의 유체역학적 거동특성에 대한 연구 사례는 OWSC의 2D 및 3D 모델링의 압력 및 플랩 회전각도에 대한 수리실험과의 비교에서 3D 모델링의 중요성을 강조한 Rafiee and Dias(2013)의 연구, OpenFOAM®을 사용하여 규칙 및 불규칙 파동에서 Oyster device(OWSC)에 대해 AMI method(arbitrary mesh interface)를 사용하여 3D 모델링을 수행하고 수리실험과의 비교를 수행한 Schmitt and Elsaesser(2015)의 연구, ANSYS FLUENT®를 사용하여 Oyster device(OWSC)에 대한 점성 및 scaling 효과를 검토한 Wei et al.(2015)의 연구, OWSC의 slamming event와 플랩 및 NWT의 wavemaker에 의해 생성된 반사의 영향에 대한 Wei et al.(2016)의 연구, Fast fictitious domain method가 적용된 CFD를 사용하여 OWSC에 PTO의 영향을 추가하여 거동특성을 검토한 Mottahedi et al.(2018)의 연구, OpenFOAM®을 사용하여 OWSC에 PTO의 영향을 추가하여 거동특성 및 발전효율을 검토한 Benites-Munoz et al.(2020)의 연구 등이 있다.
본 연구에서는 기초적인 OWSC의 거동특성에 대한 검토를 목적으로 오픈소스 CFD를 이용하여 역삼각형 플랩이 설치된 경우에 파랑과 역삼각형 플랩의 상호작용에 대한 수치해석을 수행하였다. 특히, 규칙파 내습 시 주기의 변화에 따른 역삼각형 플랩 인근의 자유수면변위 및 회전각도(Flap Rotation angle)를 산정하여 거동 특성에 대해 고찰하고, 그 결과를 수리실험과 비교·검토하여 해석성능의 타당성 및 OWSC의 관련 문제를 수치해석하기 위해 적용 가능한 수치해석모델로서의 적용성능을 검증하였다. 또한, 수치해석결과는 역삼각형 플랩 인근의 수위변동 및 유속에 대한 상세한 시‧공간 정보를 제공하며, 이에 따른 유체역학적 거동 특성을 논의하였다.
2. 수치해석이론2.1 지배방정식본 연구에 적용된 오픈소스 CFD 코드인 REEF3D(Bihs et al., 2016)는 비압축성 혼상유동(Two-Phase Flow)을 해석하기 위해 3차원 RANS(Reynolds-Averaged Navier-Stokes equations) 방정식이 운동량 및 질량보존을 규정하기 위한 연속방정식과 함께 적용된다. 지배방정식은 다음의 식(1)과 (2)에 나타내는 연속방정식과 운동량보존방정식으로 구성된다.
여기서, u는 유속벡터, ρ는 밀도, p는 압력, ν는 동점성 및 난류와점성계수, g는 중력가속도이다. 난류모델은 Wilcox(1994)에 의해 제안된 난류운동에너지 k(Turbulent kinetic energy)와 난류비소산율 ω(Specific dissipation rate)로 구성되는 2-방정식(Two-equations)의 k-ω 모델이 적용되어, 확산항에 동점성 및 난류와점성을 고려하여 계산된다.
물과 공기에 대한 혼상유동(Two-Phase Flow)의 경계면인 자유수면의 해석에는 Level-Set Method(Osher and Sethian, 1988)가 적용되며, 각 상(Phase)의 경계면 위치는 부호가 부여된 평활화된 거리함수 Φ에 의해 표현된다. Φ는 경계면에 가장 가까운 거리를 제공하고, 부호의 변화에 따라 각각의 유체에 대한 상(Phase)을 구별한다. 즉, 물과 공기의 경계면을 0으로 하여 물의 영역은 경계면을 기준으로 양(+)의 부호, 공기의 영역은 음(-)의 부호를 거리에 따라 부여한다. 거리함수 Φ 및 경계면에 대한 시간발전의 해석에는 식(3)의 이류방정식이 적용된다.
거리함수 Φ가 흐름에 의해 이류되면 부호 거리 속성이 상실됨에 따라 이 속성을 유지하고 질량 보존을 보장하기 위해 매시간 단계마다 다시 초기화되어야 한다. 따라서, Sussman et al.(1994)의 PDE(Partial Differential Equation) 기반 재초기화 방정식이 적용된다. 각 유체에 대한 밀도(ρ)와 점성(ν)은 식(4)와 식(5)를 사용하여 계산된다.
여기서, H는 Heaviside 함수, 아래첨자 w, a는 각각 물과 공기를 나타낸다.
경계면에서의 밀도와 점성의 급격한 변화는 수치적 불안정을 야기할 수 있다. 따라서 경계면에는 격자크기에 비례하는 경계면 두께 ε = 2.1△x을 부여하고, 해당 영역의 평활화를 위한 Heaviside 함수 H(식(6))를 적용한다.
식(1)~(3)의 지배방정식은 직교 교호격자를 적용한 유한차분법(Finite Difference Method, FDM)에 의해 이산방정식이 구성되며, 공간이산화에는 5차 WENO Scheme(Jiang and Peng, 2000; Jiang and Shu, 1996)이 적용되고 확산항은 2차 중앙차분으로 이산화된다. 시간이산화에는 3차 TVD Runge-Kutta Scheme(Shu and Osher, 1988)이 적용되고, 난류모델은 Implicit Euler method가 적용되어 CFL 조건에서 격자 크기에 대한 의존성을 효과적으로 제거한다. 압력은 Incremental pressure-correction algorithm(Timmermans et al., 1996)을 식(1)~(2)에 적용하여 계산된다. 이때 3차 TVD Runge-Kutta Scheme의 각 k번째 단계별 유속장 u(*)는 식(7)을 이용하여 이전 단계의 압력구배를 사용하여 예측된다.
여기서, αk = 1.0, 1/4, 2/3, βk = 0.0, 3/4, 1/3 그리고 k = 1, 2, 3을 나타낸다. 이후, HYPRE solver library(Center for Applied Scientific Computing, 2006)의 PFMG multi-grid solver(van der Vorst, 1992)로 사전조정과 함께 Fully parallelized BiCGStab algorithm을 사용하여 압력 보정항 pcorr에 대해 식(8)의 Poisson 압력방정식이 계산된다.
그리고 압력장 및 유속장은 최종적으로 식(9)와 식(10)을 이용하여 계산된다.
2.2 유체와 구조물의 상호작용 해석(Fluid-Structure Interaction, FSI)CFD 모델에서 운동하는 구조물과 상호작용하는 이상유동(Two-Phase Flow)을 수치해석하는 FSI의 기법은 격자체계의 관점에서 크게 Moving grid method와 Fixed grid method로 분류할 수 있다. Moving grid method의 경우 구조물의 형상에 따라 계산격자를 재구성함으로 구조물 인근에서 정확한 결과를 얻을 수 있지만, 중첩 격자영역의 보간 및 격자 재구성에 따른 계산비용의 증가 등의 문제점도 내포하고 있다. 반면에 Fixed grid method의 대표적인 기법으로 Peskin(1972)가 제안한 Immersed Boundary Method는 배경격자가 변형되지 않고 복잡한 형상의 구조물 이동 및 재배치시에 격자를 재생성할 필요가 없는 장점이 있다. 이를 기반으로 Fadlun et al.(2000), Uhlmann(2005), Yang and Stern(2015), Yang (2018) 등의 연구에 의해 Direct forcing method/Immersed Boundary Method의 개발 및 추가적인 발전이 수행되었다.
본 연구에 적용된 오픈소스 CFD는 유체중에 운동하는 강성 구조물의 해석방법으로 구조물의 내부 영역을 주위와 동일한 유체로 채우고 구조물의 운동을 위하여 내부의 유체 영역에 가상의 외력을 작용시키는 Yang(2018)에 의해 제안된 Continuous direct forcing Method/Immersed Boundary Method가 적용되었다(Martin at al. 2021). 유체영역을 점유하는 구조물은 Eulerian 격자영역에서 Lagrangian point를 통해 구조물 형상을 표현하게 되며, 자유수면의 해석과 동일한 Level set method가 적용된다. 구조물은 삼각형 표면격자(Triangular surface mesh)로 구성된 STL(STereoLitography format)형식으로 솔버에 입력되고, 입력된 STL 정보는 Ray-tracing algorithm을 적용하여 구조물의 내부-외부 정보를 Level set 함수 Φs로 표현한다. 생성된 Level set 함수 Φs는 식(4)~(5)를 확장하여 유체 및 구조물 영역을 구분하는데 적용된다.
여기서, 하첨자 s는 구조물을 나타낸다.
Yang(2018)에 의해 제안된 연속방정식과 운동량보존방정식은 식(13)과 식(14)로 각각 구성된다.
여기서, 외력항 f는 식(15)로 주어진다.
여기서, P(u)는 유체의 유속장을 Lagrangian point로 이루어진 구조물 내부로 투영하는 유속장을 나타낸다.
식(14)를 식(1)~(2)와 비교하면, 유일한 차이는 외력항 f와 확산항임을 알 수 있다. 따라서, 유체에서 구조물로의 전이를 나타내는 Heaviside 함수 H(Φs)와 구조물 경계면에서의 외력항 f를 적용하여 전체 영역에서 단일 방정식을 적용하여 계산된다. 이산화 단계에서 외력항 f는 새로운 시간단계 n + 1에서 식(16)로 나타낼 수 있다.
시간단계 n + 1에서의 P(u(n))은 미지수이기 때문에 유효한 근사값 P(u(n)) = u(n))를 적용하고 이전 시간 단계의 압력을 근사치로 취하면 식(17)로 나타낼 수 있다.
그런 다음 식(7)을 적용하여 식(18)로 나타낼 수 있다.
식(18)의 계산에서 식(7)을 외력항 f를 고려하지 않고 먼저 실행하여 P(u(n+1))의 근사치로 P(u(*))를 취하면 f(*)는 식(19)로 산정할 수 있다.
그리고, f(*)는 식(8)의 Poisson 압력방정식을 풀기 전에 식(7)에 추가하여 계산한다. 여기서, 구조물 내부로 투영되는 유속장 P(u(*))는 Lagrangian point로 이루어진 구조물의 운동이 병진운동과 회전운동의 조합으로 구성된다는 가정에 기초하여 해석을 수행하여 산정된다.
구조물의 병진운동은 식(20)과 같이 뉴턴의 제2법칙으로 표현된다.
여기서, FX는 구조물의 표면력, ρs는 구조물의 밀도, Vs는 구조물의 부피,
구조물의 회전운동은 고정좌표계에서 오일러 각도(Tait-Bryan angles) roll(Φ), pitch(Θ), yaw(Ψ)와 관련된 4개의 오일러 매개변수(quaternion) e = (e0, e1, e2, e3)T를 적용하여 해석된다.
(21)오일러 각도(Tait-Bryan angles)는 다음의 관계식에 의해 구할 수 있다.
(22)여기서, 4개의 오일러 매개변수(quaternion)는 eTe = 1의 조건으로 결정된다. 그리고, Shivarama and Fahren-thold(2004)이 제안한 Hamiltonian formulation을 적용하여 구조물 회전운동의 모멘텀 벡터를 산정한다. 이후, 구조물의 표면력(FX)과 모멘트(MX)는 구조물의 모든 삼각형 표면격자(Triangular surface mesh)에서의 유체력을 적분하여 계산된다.
여기서, n은 표면법선벡터, τ는 점성응력텐서, N은 삼각형 표면격자의 개수, r은 거리벡터를 나타낸다. 그리고, 힌지를 중심으로 회전하는 진자운동의 구현을 위해 Spring 계류 조건을 적용하였으며, 표면력(FX)과 모멘트(MX)에 각각 계류력 FM과 무게중심에서 힌지위치까지의 거리벡터가 고려된 모멘트 rCM × FM를 부가함으로써 구현된다. 계산된 모멘트로부터 구조물 내부로 투영되는 유속장 P(u(*))은 식(25)로부터 산정할 수 있다.
여기서,
2.3 파랑 조파 및 흡수기법파랑의 조파기법에는 Relaxation method(Jacobsen et al., 2012), 흡수기법에는 Active wave absorption method(Schäffer and Klopman, 2000)를 적용하였다.
수치파동수조의 조파경계에 적용된 Relaxation method는 파동이 생성되는 입구에 식(26)의 이완영역(Relaxation zone)을 적용하여 활성화된다.
(26)여기서,
조파경계에서 파동의 조파는 이완함수 Γ(
수치파동수조의 흡수경계 처리는 반사파를 상쇄하기 위해 흡수되는 파동유속의 반대 부호로 수정된 유속을 수치파동수조 출구에서 규정하는 Active wave absorption method를 적용하였다. 2차원 파동의 Airy 파동이론에서 천수조건을 가정하면 수평 수립자 유속은 수직축을 따라 일정하며, Active wave absorption method 경계조건은 식(27)과 같이 구현된다.
여기서, U(t)는 수정된 유속, η(t)는 흡수경계의 자유수면변위, d는 수심을 나타낸다.
3. 수리모형실험 구성수리모형실험은 피스톤형의 조파장치가 설치된 2차원조파수조(길이 30.0 m, 폭 0.7 m, 높이 0.9 m)에서 수행되었으며, 수리모형실험의 전체적인 구성을 Fig. 1에 나타낸다. 역삼각형 플랩은 조파기로부터 18.53 m 전면에 설치되었고, 일정수심 d = 0.425 m의 조건에서 피스톤형조파기로부터 Table 1에 주어진 파고 0.09 m에서 주기 1.6~4.0 s의 범위를 가지는 규칙파를 발생시켰으며, 수조의 끝단에는 반사파를 제어하기 위한 소파공이 설치되었다. 플랩은 수조 바닥에 힌지로 고정되어 있으며 입사파에 의해 앞뒤로 회전하는 진자운동을 한다. 수리모형실험에서 측정항목은 역삼각형 플랩의 전후면에서의 자유수면변위 및 회전각도(Flap Rotation)가 측정되었다. 여기서, 역삼각형 플랩 주변의 자유수면변위는 전면 3점(W1, W2 및 W3)과 후면 1점(W4)에 설치된 용량식파고계를 이용하여 측정되었고, 목표파고의 검증을 위하여 조파기의 전면(W0)에도 파고계가 설치되었다. 역삼각형 플랩의 회전각도(Flap Rotation angle)는 자이로 센서를 이용하여 측정되었다.
Fig. 2에 역삼각형 플랩의 세부 제원(a) 및 형상(b)을 나타낸다. 플랩 모델은 철제고정단, 힌지, 역삼각형 플랩의 3개 구성으로 이루어지며, 아크릴로 제작된 부유식 역삼각형 플랩의 제원은 상부 길이 15 c m, 폭 68 cm, 높이 40 c m, 중량 12.8 kg, 관성모멘트 1.27 kg·m2, 복원모멘트 8.63 N·m로 구성되고, 플랩의 하부에 철제고정단과 힌지 핀으로 결합되어 수조에 설치되었다. 따라서, y 축과 z 축으로의 거동은 제한되어지고, 힌지를 중심으로 x 축으로의 회전 거동만이 허용되는 조건이 된다. 수리모형실험의 절차 및 방법에 관한 보다 상세한 사항은 Cho et al.(2020)을 참조하기 바란다.
4. 수치해석4.1 수치파동수조 구성
Fig. 3에 나타내는 바와 같이 수치해석을 위한 수치파동수조의 구성은 수리모형실험 결과를 정량적으로 비교하기 위해 구조물 및 입사파랑 제원은 수리모형실험과 동일하게 설정하였다. 단, 계산의 효율성과 적용된 수치모델이 무반사 조파 기능이 포함되어 있음을 고려하여 수치파동수조의 길이는 13.96 m, 폭은 0.05 m로 감소시켜 설정하며, 높이는 1.0 m의 영역으로 설정하였다. 격자크기는 △x = 0.005~0.03 m, △y = 0.01m, △z = 0.01m의 가변격자체계로 구성하여, 적용된 격자의 총 개수는 423,594개이다. 구성된 격자에 대한 Courant 상수는 0.3 이하가 되도록 자동으로 시간 간격을 조정하며 수치해석이 수행되고 계산의 효율을 위해 영역분할에 의한 MPI 병렬계산을 적용하였다. 수조의 바닥면 및 구조물의 표면경계는 No-slip 조건을 적용하였다. 대상파랑에 대한 수치조파에는 Cnoidal파 이론을 적용하였으며, 조파(1L)경계는 Relaxation Method, 흡수경계는 Active wave absorption method(AWA)를 적용하였다.
4.2 역삼각형 플랩 구성역삼각형 플랩은 상부 길이 15 cm, 폭 5 cm, 높이 40 cm 형상의 STL 형식으로 구성되어 솔버에 입력되고, 입력된 Fig. 4(a)의 STL 정보는 Ray-tracing algorithm을 적용하여 구조물의 내부-외부 정보를 Fig. 4(b)의 Level set 함수 Φs로 표현하여 유체 및 구조물 영역을 구분하게 된다. CFD 모델 내에서 Φs = 1인 경우를 구조물로 취급하게 된다. 힌지조건으로는 Spring 계류를 적용하였으며, 힌지위치에서 역삼각형 플랩의 하단까지 Spring 계류라인으로 연결하여 힌지를 중심으로 회전하는 진자운동을 구현하였다. 따라서, 역삼각형 플랩의 거동은 2자유도 운동(surge, pitch)으로 제한된다.
4.3 자유수면변위
Fig. 5~6은 Table 1의 계산조건에 대하여 역삼각형 플랩의 전면과 배후의 자유수면변위에 대해 수리실험 및 수치해석 결과를 비교하여 나타낸 것이다. 자유수면변위의 측정위치는 Fig. 3에 제시한 바와 같이 역삼각형 플랩의 전면 3점(W1(x = 9.00 m), W2(x = 9.50 m) 및 W3(x = 9.70 m))과 후면 1점(W4(x = 12.50 m))에 위치한다.
Fig. 5(a)와 Fig. 5(b)에 나타내는 주기가 비교적 작은 Case1(T = 1.6 s) 및 Case2(T = 2.0 s)의 수면변동은 역삼각형 플랩의 전면(W1, W2, W3)과 후면(W4)에서 모두 비교적 선형적인 파형을 유지하는 것을 보인다. 이는 진행하는 파동과 역삼각형 플랩의 상호작용에 의한 거동이 파동장을 크게 교란시키지 않고 연행되고 있음을 보여준다.
다음으로 Fig. 5(c)에 나타내는 주기가 소폭 증가하는 Case3(T = 2.4 s)의 수면변동에서는 파봉에 비해 파곡 부분이 평탄해지며 경사가 커지는 파형의 상하 비대칭성이 나타나는 것이 관찰된다. 그리고 점차 주기가 증가하는 Fig. 5(d) 및 Fig. 6(a)~Fig. 6(d)에 보이는 Case4(T = 2.8 s)~Case8(T = 4.0 s)의 수면변동은 파형의 상하·전후 비대칭성 및 비선형성이 크게 나타나고 있고, 특히 파형 사이에 고주파수 파형성분이 발달됨을 확인할 수 있다. 이는 역삼각형 플랩의 부력에 의한 복원력으로 인해 발생되는 회전운동 및 관성운동이 진행하는 파동과 상호작용하여 생성되는 반사파동의 영향으로 판단된다. 전반적으로 주기가 길어질수록 비대칭성과 비선형성이 강하고 고주파수 파형성분이 발달되는 수위변동이 형성되는 것을 알 수 있다.
전반적으로 주기가 길어질수록 비대칭성과 비선형성이 강하고 고주파수 파형성분이 발달되는 수위변동이 형성되는 것을 알 수 있으며, 수리실험과 수치해석결과의 대응성은 자유수면변위의 진폭과 위상에서 약간의 편차를 보이고 있으나, 시간발전에 따른 역삼각형 플랩 주변에서 발생하는 일련의 파랑변형과정을 양호하게 재현하고 있다는 것을 확인할 수 있다.
4.4 플랩회전각도
Fig. 7은 역삼각형 플랩의 x 축 방향 회전운동(pitch)에 의한 회전각도(Flap Rotation angle)에 대해 수리실험 및 수치해석 결과를 비교하여 나타낸 것이다. 그래프의 세로축에 나타내는 회전각도에서 양의 값(+)은 시계방향 회전, 음의 값(-)은 반시계방향 회전을 나타낸다. 전반적으로 회전각도의 시간발전에 따른 양상은 모든 Case에서 비교적 선형적으로 나타나고, Case1(T = 1.6 s)에서 Case8(T = 4.0 s)로 주기가 증가함에 따라 시계방향 및 반시계방향의 회전각도는 증가되어 나타난다.
Fig. 8은 시계방향 및 반시계방향 회전각도의 최대치를 나타낸 것으로 시계방향 회전의 경우, Case1(T = 1.6 s)과 Case8(T = 4.0 s)에서 수리실험 결과는 13°와 29°, 수치해석 결과는 16°와 27°로 각각 16°, 11°의 회전각도 증가가 나타난다. 그리고 반시계방향 회전의 경우, 수리실험 결과는 -13°와 -29°, 수치해석 결과는 -10°와 -22°로 각각 16°, 12°의 회전각도 증가가 나타난다. 이때 회전각도는 Case5(T = 3.0 s)까지 지속적으로 증가하다가 Case6(T = 3.2 s)을 기점으로 증가폭이 둔화되어 Case8(T = 4.0 s)로 갈수록 일정각도로 수렴되어 나타나는 결과를 보인다. 이는 본 연구에서 적용하는 실험 Case가 주기의 변화만을 고려하므로, 실험 Case의 변화로 인한 수평유속의 증가는 크지 않고 역삼각형 플랩에 작용하는 외력의 지속시간 증가와 복원력과의 평형으로 야기되는 결과로 판단된다.
4.5 자유수면변위 및 플랩회전각도의 오차평가자유수면변위 및 플랩회전각도에 대한 수치해석결과와 수리실험결과의 정량적인 오차평가를 위해 정규화된 평균 제곱근 오차(Normalized Root Mean Squared Error, 이하 NRMSE)를 비교하였다. NRMSE의 계산은 식(28)을 적용하였고, Case별 NRMSE를 Table 2에 나타내었다.
여기서, Si는 i번째 수치해석결과, Oi는 i번째 수리실험결과, n은 총 데이터수이다.
Table 2에 보이는 바와 같이 수리실험과 수치해석결과의 대응성은 자유수면변위의 경우 4.00~16.96%, 플랩회전각도의 경우 3.67~15.70%의 NRMSE 수준에서 재현성을 확보하는 것을 확인할 수 있다.
4.6 플랩거동특성본 수치해석의 결과 중 Case5(T = 3.0 s)의 한 주기의 파동(t/Ti = 1/10)에 대한 역삼각형 플랩 주변의 유속벡터 및 수면 변동에 대한 Snapshot을 Fig. 9~10에 제시한다. 이때, 입사파랑은 좌측에서 우측으로 진행되며, 그림에서 3차원 Snapshot은 역삼각형 플랩의 회전운동에 대한 거동특성을 명확하게 파악하기 위해 y 축을 10배 확장시켜 표현한 것이다.
Fig. 9에서 내습하는 파랑의 파봉이 역삼각형 플랩으로 접근함에 따라 유속벡터로부터 확인되는 우측방향으로 작용하는 수평유속에 의해 역삼각형 플랩은 시계방향 회전운동을 시작하는 것을 확인할 수 있다(Fig. 9(a), (b) 참조). 파랑이 계속 진행하여 역삼각형 플랩이 파곡과 파봉의 중간지점에 위치하였을때 시계방향 회전각도가 최대로 나타나는 것이 Fig. 9(c)를 통해 확인된다. 그리고 Fig. 9(d), (e)에서 작용하는 수평유속이 좌측방향으로 전환되며 부력에 의한 복원력으로 인해 원위치로 복귀하려는 반시계방향 회전운동이 이행되는 과정을 확인할 수 있다.
Fig. 10에서 역삼각형 플랩이 파곡에 위치하는 순간에 회전각도가 원위치로 되는 것이 Fig. 10(a)을 통해 확인되고, 관성력과 유속벡터로부터 확인되는 좌측방향의 수평유속에 의해 역삼각형 플랩의 반시계방향 회전운동이 가속된다(Fig. 10(b), (c) 참조). 시계방향 회전운동과 마찬가지로 역삼각형 플랩이 파봉과 파곡의 중간지점에 위치하였을때 반시계방향 회전각도가 최대로 나타나는 것이 Fig. 10(c)를 통해 확인된다. 그리고 Fig. 10(d), (e)에서 작용하는 수평유속이 우측방향으로 전환되며 부력에 의한 복원력으로 인해 원위치로 복귀하려는 시계방향 회전운동이 이행되는 과정을 확인할 수 있다. 이상의 결과로부터 파랑과 역삼각형 플랩의 상호작용에 의한 유체역학적 거동 특성을 확인할 수 있다.
5. 결 론본 연구에서는 기초적인 OWSC의 거동특성에 대한 검토를 목적으로 오픈소스 CFD를 이용하여 파랑장하 역삼각형 플랩이 설치된 경우에 파랑과 역삼각형 플랩의 상호작용에 대한 수치해석을 수행하였다. 규칙파 내습시 주기의 변화에 따른 역삼각형 플랩 인근의 자유수면변위 및 회전각도(Flap Rotation angle)를 산정하여 거동 특성에 대해 고찰하고, 그 결과를 수리실험과 비교·검토하여 해석성능의 타당성 및 OWSC의 관련 문제를 수치해석하기 위해 적용 가능한 수치해석모델로서의 적용성능을 검증하였다. 그 결과를 요약하면 다음과 같다.
1) 역삼각형 플랩의 전면과 배후의 자유수면변위는 주기가 길어질수록 비대칭성과 비선형성이 강하고 고주파수 파형성분이 발달되는 수위변동이 형성되는 것을 확인하였다. 이는 역삼각형 플랩의 부력에 의한 복원력으로 인해 발생되는 회전운동 및 관성운동이 진행하는 파동과 상호작용하여 생성되는 반사파동의 영향으로 판단된다.
2) 역삼각형 플랩의 회전각도는 주기가 길어질수록 지속적으로 증가하다가 Case6(T = 3.2 s)을 기점으로 증가폭이 둔화되어 일정각도로 수렴되어 나타나는 것을 확인하였다. 이는 본 연구에서 적용하는 실험 Case가 주기의 변화만을 고려하 므로, 실험 Case의 변화로 인한 수평유속의 증가는 크지 않고 역삼각형 플랩에 작용하는 외력의 지속시간 증가와 복원력과의 평형으로 야기되는 결과로 판단된다.
3) 역삼각형 플랩 주변의 유속벡터 및 수면변동에 대한 Snapshot의 결과로부터 파랑과 역삼각형 플랩의 상호작용에 의한 유체역학적 거동 특성을 확인하였다.
4) 자유수면변위 및 회전각도에 대한 수리실험과 수치해석 결과의 비교에서 약간의 편차를 보이고 있으나, 시간발전에 따른 역삼각형 플랩 주변에서 발생하는 일련의 파랑변형 및 역삼각형 플랩의 거동 특성을 양호하게 재현하는 것을 확인하였다. 이상의 결과로부터 본 연구에서 적용하고 있는 오픈소스 CFD의 역삼각형 플랩에 대한 해석으로의 적용성이 확인되었다.
본 연구에서는 기초적인 OWSC의 거동특성을 해석하기 위해 구조물 주면의 자유수면변위와 회전각도 등으로부터 CFD의 적용가능성을 검토하였지만 향후 진자의 회전속도를 포함한 다양한 동역학적 특성에 대한 상세한 수치해석으로의 확장이 필요할 것으로 판단된다.
Fig. 9.Snapshot of the velocity vectors and free surface elevation around the OWSC for Case5 (t/T = 1/10~5/10). 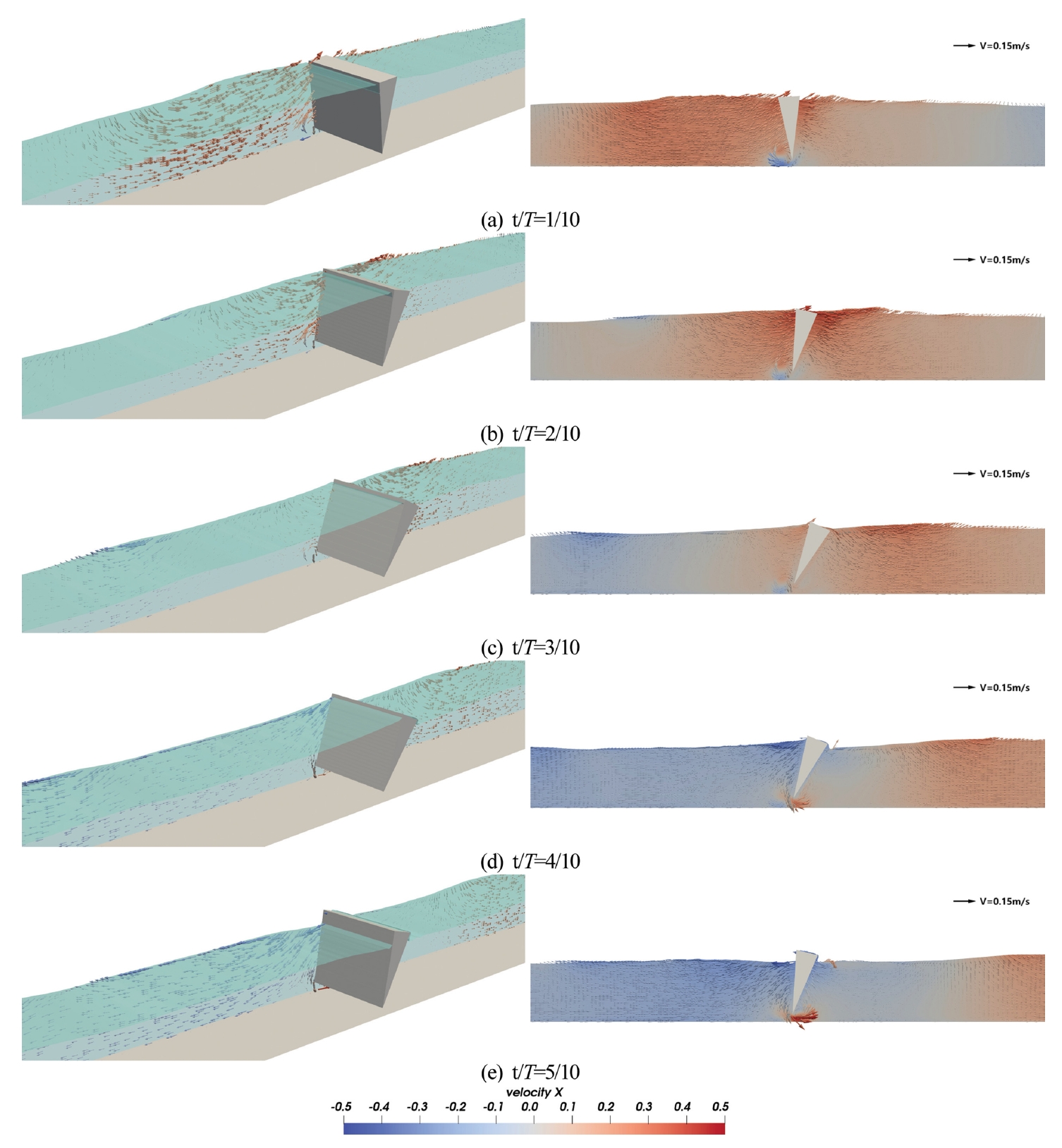
Fig. 10.Snapshot of the velocity vectors and free surface elevation around the OWSC for Case5 (t/T = 6/10~10/10). 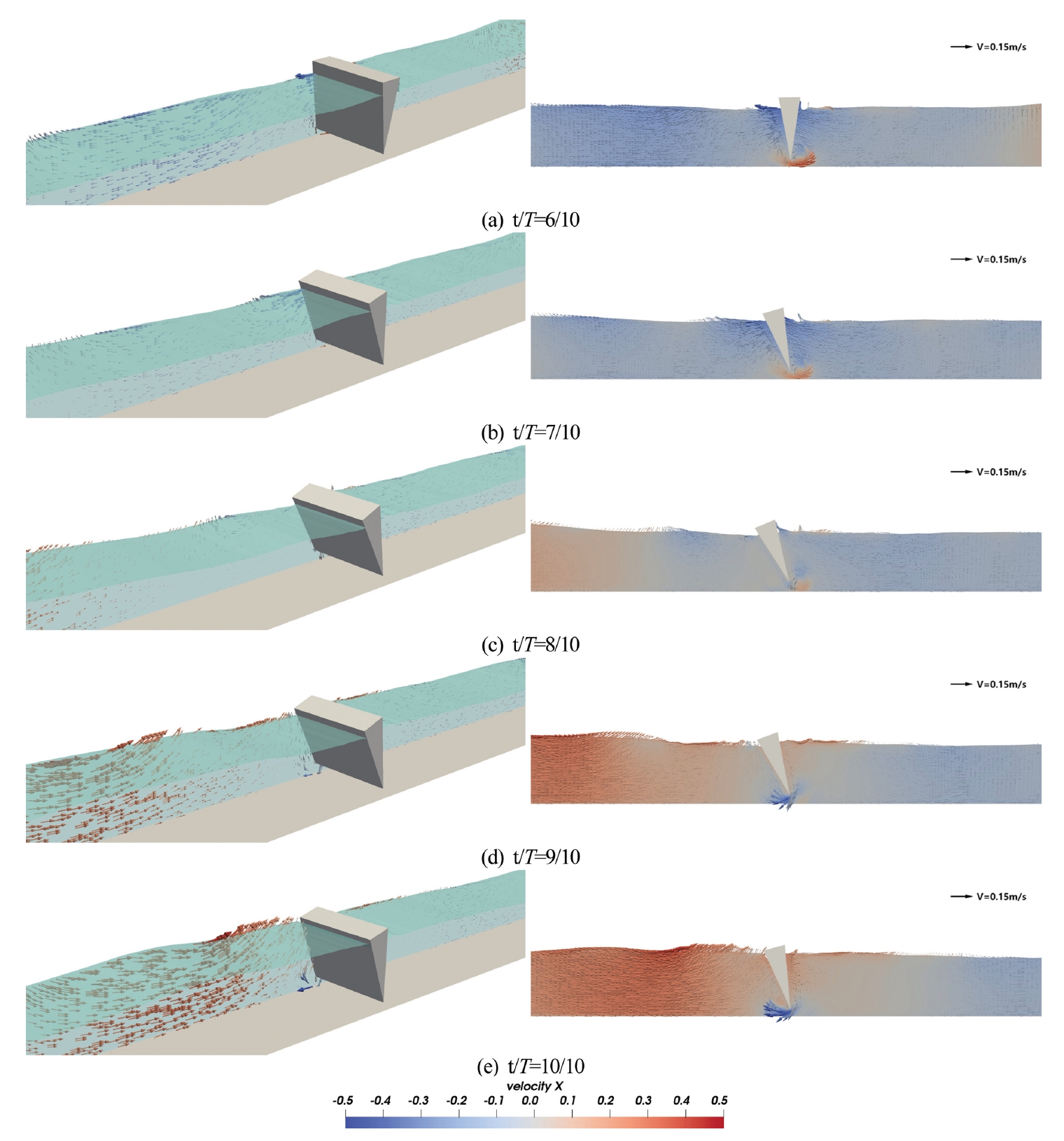
Table 1.Conditions of incident waves Table 2.Results of NRMSE for water surface elevations and flap rotation angle ReferencesAEA. (2006). Review and analysis of ocean energy systems development and supporting policies.IEA’s, Implementing Agreement on Ocean Energy Systems. 28th June.
Barker, G., Vantorre, M., Banasiak, R., Beels, C., De Rouck, J.. (2007). Numerical modelling of wave energy absorption by a floating point absorber system, Proceedings of the Seventeenth International Offshore and Polar Engineering Conference. Lisbon, Portugal: July 1-6.
Bihs, H., Kamath, A., Alagan Chella, M., Aggarwal, A., Arntsen, Ø.A. (2016). A new level set numerical wave tank with improved density interpolation for complex wave hydrodynamics, Computers & Fluids, 140, 191-208.
Bridgwater Court, J., Chandel, D., Sell, N., Plummer, A., Hilli, A.. (2017). Modelling of Array Interactions for a Curved OWSC using OpenFOAM, in Proc, of the 12th European Wave and Tidal Energy Conference. Cork, Ireland.
Benites-Munoz, D., Huang, L., Anderlini, E., Marín-Lopez, J.R., Thomas, G. (2020). Hydrodynamic modelling of an oscillating wave surge converter including power take-off, Journal of Marine Science and Engineering, 8(10):771 https://doi.org/10.3390/jmse8100771.
Center for Applied Scientific Computing. (2006. HYPRE High Performance Preconditioners - User’s Manual). Lawrence Livermore National Laboratory, Livermore, CA, USA.
Cho, Y.-H., Nakamura, T., Mizutani, N. and Lee, K.-H.(2020). An experimental study of a bottom-hinged wave energy converter with a reflection wall in regular waves—focusing on behavioral characteristics. Applied Sciences, 10, 6734.
Engineering Business Ltd., (2005). EB Frond wave energy converter - phase 2. DTI Report URN05/865.
EPRI. (2005). Ocean tidal and wave energy. Renewable Energy Technical Assessment Guide-TAG-RE.
Fadlun, E.A., Verzicco, R., Orlandi, P., Mohd-Yusolf, J. (2000). Combined immersed-boundary finite-difference methods for three-dimensional complex flow simulations, Journal of Computational Physics, 161, 35-60.
Falnes, J. (2007). Review a review of wave-energy extraction, Marine Structures, 20, 185-201.
FEMP. (2009. Ocean energy technology overview). The U.S. Department of Energy, uly DOE/GO-102009-2823.
Flocard, F., Finniga, T.D.. (Experimental investigation of power capture from pitching point absorbers, in Proc, of the 8th European Wave and Tidal Energy Conference. Uppsala, Sweden.
Falcão, A.F.O. (2010). Wave energy utilization : A review of the technologies, Renewable and Sustainable Energy Reviews, 14, 899-918.
ISSC. (Specialist committee V.4, ocean wind and wave energy utilization, 16th International Ship and Offshore Structures Congress. August 20th-25th. Southampton, UK: 2.
Jiang, G., Shu, C. (1996). Efficient implementation of weighted ENO schemes, Journal of Computational Physics, 126(1):202-228.
Jiang, G., Peng, D. (2000). Weighted ENO schemes for Hamilton Jacobi equations, SIAM Journal of Scientific Computing, 21, 2126-2143.
Jacobsen, N.G., Fuhrman, D.R., Fredsøe, J. (2012). A wave generation toolbox for the open-source CFD library: OpenFOAM, International Journal for Numerical Methods in Fluids, 70, 1073-1088.
Lee, K.H., Kim, D.S., Yook, S.M., Jung, Y.H., Jung, I.H. (2014). Dynamic response analysis of pressurized air chamber breakwater mounted wave-power generation system utilizing oscillating water column, Journal of Korean Society of Coastal and Ocean Engineers, 26(4):225-243.
Mottahedi, H.R., Anbarsooz, M., Passandideh-Fard, M. (2018). Application of a fictitious domain method in numerical simulation of an oscillating wave surge converter, Renewable Energy, 121, 133-145.
Martin, T., Tsarau, A., Bihs, H. (2020). A Numerical Framework for Modelling the Dynamics of Open Ocean Aquaculture Structures in Viscous Fluids, Applied Ocean Research, DOI: 10.1016/j.apor.2020.102410.
Osher, S., Sethian, J. (1988). Fronts propagating with curvaturedependent speed: algorithms based on hamilton-jacobi formulation, Journal of Computational Physics, 79, 12-49.
Powertech. (2009). Ocean energy: Global technology development status. IEA-OES Document T0104.
Rafiee, A., Dias, F.. (2013). Two-dimensional and three-dimensional simulation of wave interaction with an oscillating wave surge converter, in Proc, of the International workshop on water waves and floating bodies (IWWWFB). Marseille.
Shu, C., Osher, S. (1988). Efficient implementation of essentially non-oscillatory shock-capturing schemes, Journal of Computational Physics, 77(2):439-471.
Sussman, M., Smereka, P., Osher, S. (1994). A level set approach for computing solutions to incompressible two-phase flow, Journal of Computational Physics, 114, 146-159.
Schäffer, H.A., Klopman, G. (2000). Review of multidirectional active wave absorption methods, Journal of Waterway, Port, Coastal, and Ocean Engineering, 126, 88-97.
Shivarama, R., Fahrenthold, E. (2004). Hamilton’s equations with euler parameters for rigid body dynamics modeling, J. Dyn. Sys., Meas., Control, 126, 124-130.
Schmitt, P., Elsaesser, B. (2015). On the use of OpenFOAM to model oscillating wave surge converters, Ocean Engineering, 108, 98-104.
Timmermans, L., Minev, P., Van De Vosse, F. (1996). An approximate projection scheme for incompressible flow using spectral elements, International Journal for Numerical Methods in Fluid, 22, 673-688.
Tan Loh, T., Greaves, D., Mäki, T., Vuorinen, M., Simmonds, D., Kyte, A.. (2016). Numerical Modelling of the WaveRoller Device Using OpenFOAM®, in Proc, of the 3rd Asian Wave & Tidal Energy Conference (AWTEC). Singapore.
Tan Loh, T.. (2018). Assessments of Wave-Structure Interactions for an Oscillating Wave Surge Converter using CFD, PhD Thesis. University of Plymouth.
Uhlmann, M. (2005). An immersed boundary method with direct forcing for the simulation of particulate flows, Journal of Computational Physics, 209, 448-476.
van der Vorst, H. (1992). BiCGStab: A fast and smoothly converging variant of Bi-CG for the solution of nonsymmetric linear systems, SIAM Journal of Scientific Computing, 13, 631-644.
Wei, Y., Abadie, T., Henry, A., Dias, F. (2016). Wave interaction with an oscillating wave surge converter. Part II: Slammin, Ocean Engineering, 113, 319-334.
Whittaker, T.J.T., Folley, M. (2012). Nearshore oscillating wave surge converters and the development of Oyster, Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 370, 345-364.
Wilcox, D.C. (1994). Simulation of transition with a two-equation turbulence model, AIAA Journal, 32(2):247-255.
Yang, J., Stern, F. (2015). A non-iterative direct forcing immersed boundary method for strongly-coupled fluid-solid interactions, Journal of Computational Physics, 295, 779-804.
Yang, L. (2018). One-fluid formulation for fluid structure interaction with free surface, Comput. Methods Appl. Mech. Engrg, 332, 102-135.
|
|
|||||||||||||||||||||||||||||||||