1. 서 론
고정식 해상풍력터빈과 같이 기초가 해저면에 고정되어 있는 구조물에서 발생하는 문제점 중의 하나는 세굴에 의한 침식현상이다. 해류 및 파랑에 노출된 기초에서 발생하는 세굴 현상은 유체의 흐름과 구조물 사이의 상호작용으로 인해 해저 입자가 유실되는 현상으로 정의할 수 있으며, 설계 시 고려해야 하는 중요한 요소이다. 이러한 세굴이 발생하면 풍하중과 파랑하중에 의해 작용하는 수평하중과 모멘트 하중을 견뎌야 하는 해상풍력터빈의 안정성을 저하시키며, 이에 대한 대응 연구는 매우 중요하다. 이러한 해상풍력터빈의 경우 교량 교각의 경우처럼 세굴 현상에 대한 연구가 광범위하게 진행되지는 않았지만, 세굴 현상에 대한 연구가 지속적으로 진행되고 있다. Ko et al.(2015)는 HeMOSU-1호 해상 기상탑 재킷 구조물에 대해서 수치해석을 진행한 후 현장 관측값과 비교하였고, Lee(2013)는 세굴에 따른 고정식 해상풍력터빈의 동적응답을 분석하여 모노파일로 지지되는 해상풍력터빈이 세굴에 의하여 가장 큰 영향을 받는 것을 제시한 바 있다. 해외 연구사례로는 실제 몇 년 동안 운영한 해상풍력터빈에 대하여 세굴 깊이를 측정한 바 있으며, Margheritini et al.(2006)은 세굴에 대한 쇄파 및 조류의 영향을 축소 모형실험을 수행하여 분석하였다. 한편 세굴 깊이와 관련하여 해상풍력터빈에 대한 DNV-OS-J101(DNV 2014) 기준에서는 말뚝 직경의 1~1.5배까지 고려하도록 하고 있으며, 실제 북해에 설치된 모노포드 형식의 해양구조물에 대한 세굴과 관련된 기존 문헌(Peter, 1986)에서는 세굴 깊이가 말뚝 직경의 1배 이내이었음을 보고한 바 있다. 이러한 기존연구들은 세굴에 대해 결정론적 설계법에 의한 연구가 대부분이었으며, 확률론적 연구는 거의 진행되지 않고 있다.
따라서 본 연구에서는 해상풍력터빈 지지구조물의 확률론적 평가를 위한 세굴위험도 평가기법을 제안하고자 한다. 이를 위해 지진에 대한 위험도를 평가하는 방법 중 하나인 지진위험도 평가기법을 변형하여 세굴취약도 평가방법을 제시하였다. 지진위험도는 확률적으로 평가할 수 있는데, 이를 위해서 임의의 지역에 지진이 발생할 확률과 그러한 지진이 발생하였을 때 구조물에 손상이 발생할 확률, 즉 지진취약도를 이용한다. 지진취약도는 1980년대 초 원자력발전소의 확률론적 지진 안정성 분석을 위하여 개발되었으며(Kennedy and Ravindra, 1984; Shinozuka et al., 1984), 일반 토목 구조물에도 점차 적용되고 있는 추세이며, 국내에도 그 분석 사례가 증가하고 있다. 이러한 지진위험도 분석기법을 적용하기 위하여, 본 연구에서는 세굴 깊이 변화에 대한 해상풍력터빈의 취약도 곡선을 산정하고, 세굴 깊이의 발생확률과 결합하여 세굴위험도를 평가하고자 한다.
세굴 취약도 곡선을 산정하기 위하여 석션버켓을 탑재한 3MW 해상풍력터빈에 대하여 동적 해석을 수행하였으며, 하중은 풍하중과 파랑하중을 적용하였다. 이를 통해 세굴 깊이에 대한 세굴취약도 곡선을 산정하였다. 또한 세굴이 발생할 확률과 세굴에 의한 구조물의 세굴취약도 곡선을 결합하여 세굴위험도를 분석하고자 한다.
2. 세굴위험도
2.1 세굴 깊이 결정
최대 세굴 깊이 결정은 여러 가지 경험공식에 의존하고 있으나 경험식 산출에 사용된 하상입자와 구조물의 크기, 유속 범위의 제한성 등으로 각 경험식에 따라 세굴 깊이 예측에 큰 차이를 보이고 있다.
본 연구에서 사용한 경험식은 유의파고, 유의 주기, 조류속 등 해양 환경조건을 고려하기 적합한 Sumer and Fredsoe (2001)가 제안한 다음 식을 이용하여 세굴 깊이를 계산하였다.
여기서, s : 세굴 깊이(m)
sc/D : current-only case(0.7 or 1.4 추천, 0.7 적용)
D : 파일의 직경(m)
KC : u m a x T D = 2 πa D
A : 0 . 03 + 0 . 75 U c w 2 . 6
B : 6exp(-4.7Ucw)
Ucw : ( U c U c + U m )
Uc : /2 위치에서의 조류속
umax : 해저면에서의 유속
T : 유의주기
a : 수립자의 진폭
2a는 한 주기 동안의 물입자의 궤도운동이므로 KC 수가 작다는 것은 구조물의 크기에 비해 물입자의 궤도가 작다는 것을 의미한다. KC 수가 매우 작다면 말굽형 와류를 형성하지 못할 정도로 바닥 경계층 두께가 작게 되어 국부세굴은 발생하지 않을 것이다.
2.2 확률분포의 추정
본 연구에서 세굴 깊이의 확률분포를 추정할 때 정규분포로 가정하여 분포를 추정하였다. 중심극한정리에 의해 독립적인 확률변수는 정규분포에 가까워지며, 다수의 공학 및 과학 분야에서 사용된다. 확률변수 X에 대한 확률밀도함수는 식(2)과 같다.
여기서 이 분포의 모수는 평균인 μX와 표준편차인 σX이며, 분포를 나타낼 경우 일반적으로 N(μ, σ)로 쓰인다.
2.3 세굴취약도
세굴이 발생했을 때 구조물은 손상이 발생할 수도 또는 그렇지 않을 수도 있다. 특정 구조물에 대하여 세굴이 발생했을 때 구조물에 손상이 발생할 확률을 설명하는 것이 취약도이다(Shinozuka et al., 2000). 이러한 취약도 곡선은 대수정규분포함수로 표현하며 대수정규분포함수의 두 가지 주요 계수인 중간값과 대수표준편차는 최우도 추정법으로 구한다. 여러 가지 손상단계 가운데 k번째 손상에 대하여 취약도 곡선을 식(3)과 같이 대수정규분포함수로 나타낼 수 있다.
여기서, Φ는 표준정규분포의 누적확률분포함수이며, ck는 중간값, ζk는 대수표준편차이다.
손상을 입은 구조물과 손상을 입지 않은 구조물을 대상으로 우도함수(likelihood function)는 대수정규분포함수로 가정한 식에 모든 데이터에 대해 적용시켜 구할 수 있다. 손상이 발생되었을 때에는 손상에 대한 확률 [Fk(ai)]을 증가시키고 손상이 발생되지 않았을 경우에는 손상이 일어나지 않을 확률 [1-Fk(ai]을 증가시키도록 식(4)와 같이 정의한다.
여기서, xi는 구조물의 손상여부에 따라 손상이 없으면 0 손상이 있으면 1을 입력하여 각각 무손상과 손상의 확률을 누적시킴으로써 최우도함수를 산정할 수 있다. 대수함수는 단조증가함수이므로 우도를 최대화하는 상태는 로그를 취해 동일한 위치에서 최대가 되므로 식(5)와 같이 로그를 취한다.
중간값과 대수표준편차는 lnL을 최소 또는 최대화하는 최적화문제를 풀어서 구할 수 있으며 이 위치에서는 식(6)의 조건을 만족한다.
2.4 세굴 위험도
세굴 깊이에 대한 확률과 세굴에 의한 구조물의 세굴취약 도곡선 Fk(a)와 결합하여 세굴에 의한 위험도를 식(7)과 같이 구할 수 있다.
여기서, amax는 물리적으로 발생 가능한 최대세굴 깊이이며, 구조물을 T년 동안 사용할 때, 이 기간 동안의 세굴 위험도는 전체 확률에서 세굴에 의해 한 번도 파손되지 않을 확률을 제외하여 구할 수 있으므로 다음 식(8)과 같다.
최종적으로 지수함수의 무한급수를 이용하면 T년 동안의 총 세굴위험도를 다음 식(9)과 같이 간단히 표현할 수 있다.
2.5 파랑 하중
여기서, CD, CI는 항력계수 및 관성력계수이며, ρw는 해수의 밀도, u는 물입자의 속도, ∂u/∂t는 물입자의 가속도이다.
실제 파랑은 하나의 파고와 주기를 갖는 규칙파가 아니라 파고와 주기가 불규칙적 이므로 이러한 불규칙 파랑하중에 의한 해양 구조물의 응답을 얻기 위해서는 파랑 스펙트럼을 이용한다. 파랑스펙트럼은 다양한 파고 및 주기를 갖는 규칙파의 합으로 간주하여 주파수와 파의 에너지로 나타낸 것이며, 본 연구에서는 Bretschneider가 제안한 식(11)을 적용하였다.
여기서, H1/3은 유의파고, H1/3은 유의주기, f는 파랑 주파수이다.
2.6 조류속
조류는 달과 태양 등 천체의 인력에 의해 발생하는 Tidal current와 바람이 작용함에 따라 해수면과의 항력으로 인해 발생하는 Wind-generated current로 구분되며 식(12)와 같이 두 조류속을 합산하여 설계 조류속을 산정하게 된다.
여기서, v(z) = total current velocity at level z
z = vertical coordinate from still water level
vtide0 = tidal current at still water level
vwind0 = wind-generated current at still water level
h = water depth from still water level
h0 = reference depth for wind-generated current; h0 = 50 m
제시된 vwind0 값이 없는 경우 식(13)과 같이 추정할 수 있다.
여기서, k = 0.015~0.03
U0 = 1-hour mean
3. 수치해석
3.1 대상 구조물
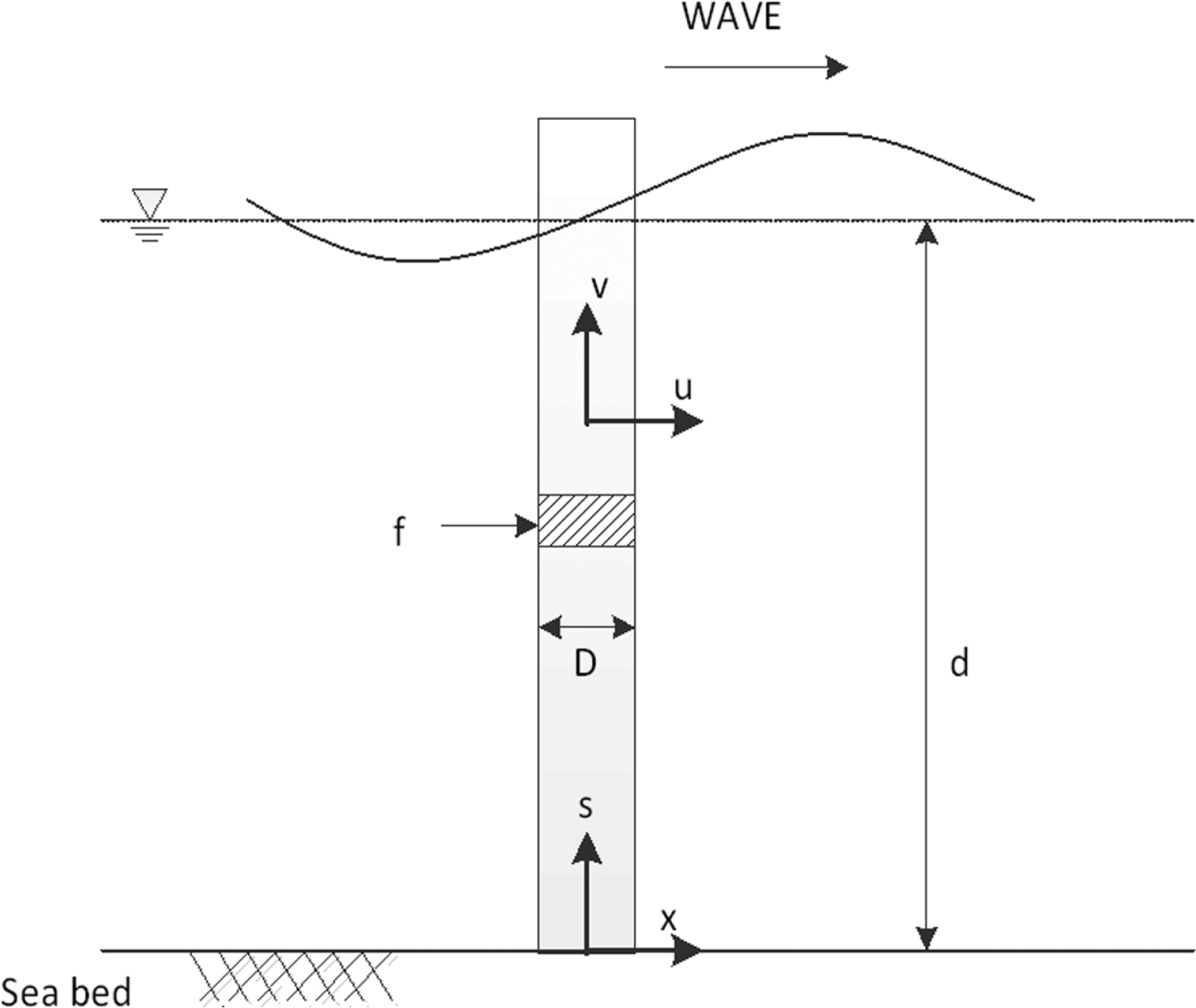
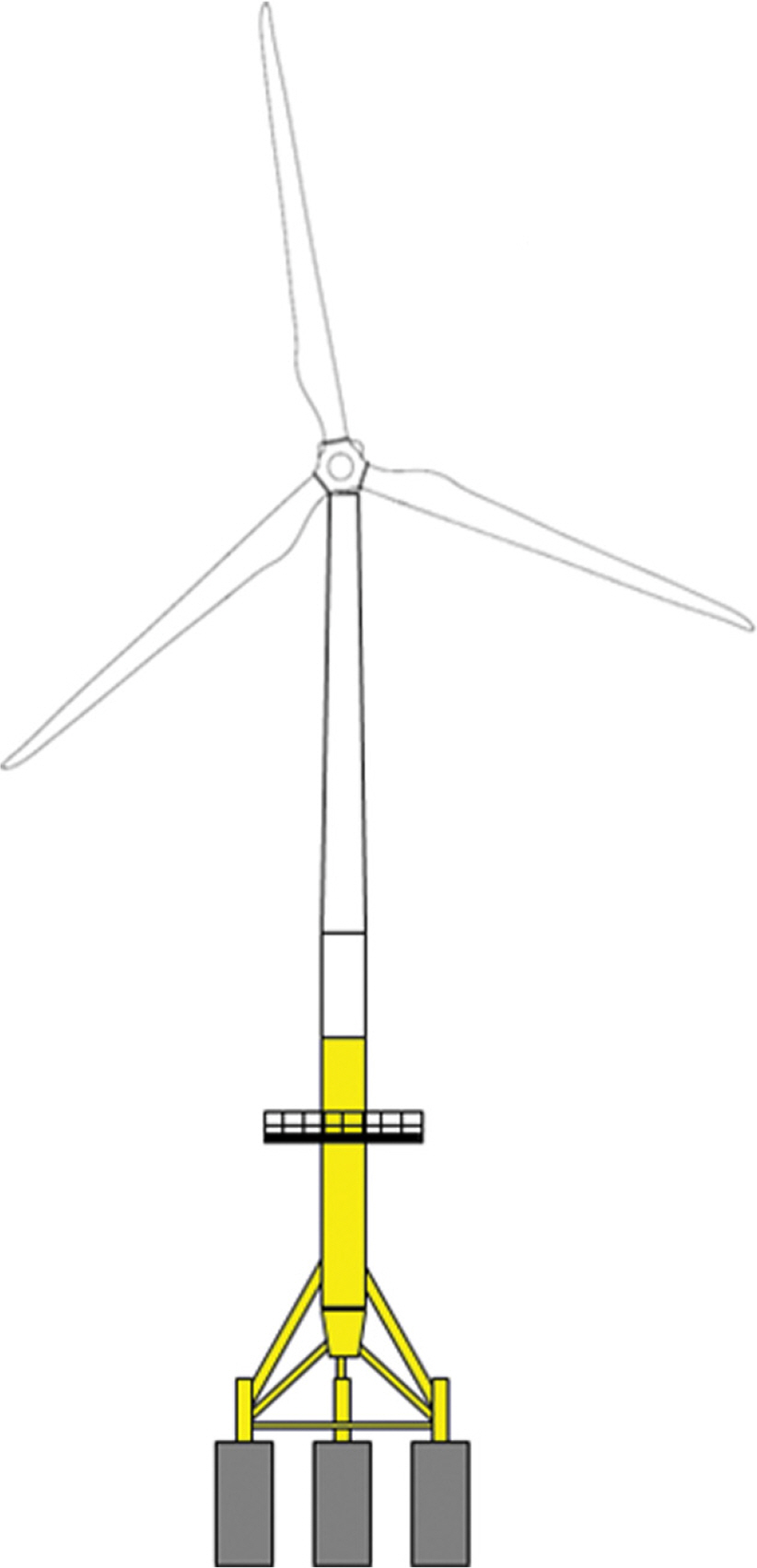
해상풍력발전기는 Fig. 2와 같이 지지구조물, 타워, 나셀, 블레이드로 구성되어 있다. 석션버켓 기초(Suction bucket foundation)는 내부의 유체를 외부로 강제 배출시킬 때 발생하는 내외부의 압력차를 이용하여 설치하는 기초로 설치가 비교적 간단하고 시공속도가 빠르며, 경제적인 기초공법으로 알려져 있다.
본 연구에 사용된 모델은 3 MW 해상풍력발전기로 하부구조물은 트라이포드 석션버켓 기초형식으로 구성되어 있으며, 구조물의 제원은 Table 1과 같다. 석션버켓의 직경은 6 m 길이는 12 m이다.
3.2 설계 지반 정수
석션버켓을 탑재한 해상풍력터빈은 석션버켓이 지반에 관입되어 지반과 관입된 말뚝의 상호작용에 의해 지지력이 결정되기 때문에 지반의 설계정수 산정이 중요하다. 본 연구에서 사용된 지반 정수는 군산 남방파제 인근의 착저식 콘 관입시험 결과와 지반조사 결과를 이용하여 적용하였으며, 각 층의 설계지반정수는 Table 2와 같다.
세굴의 침식 효과를 모사하기 위해서 본 연구에서는 지반을 3차원 요소로 모델링하여 각각의 해석 단계에서 발생된 세굴 깊이만큼의 구조물 주변의 지반 요소를 제거하여 침식의 효과를 고려하였다.
3.3 추력 산정
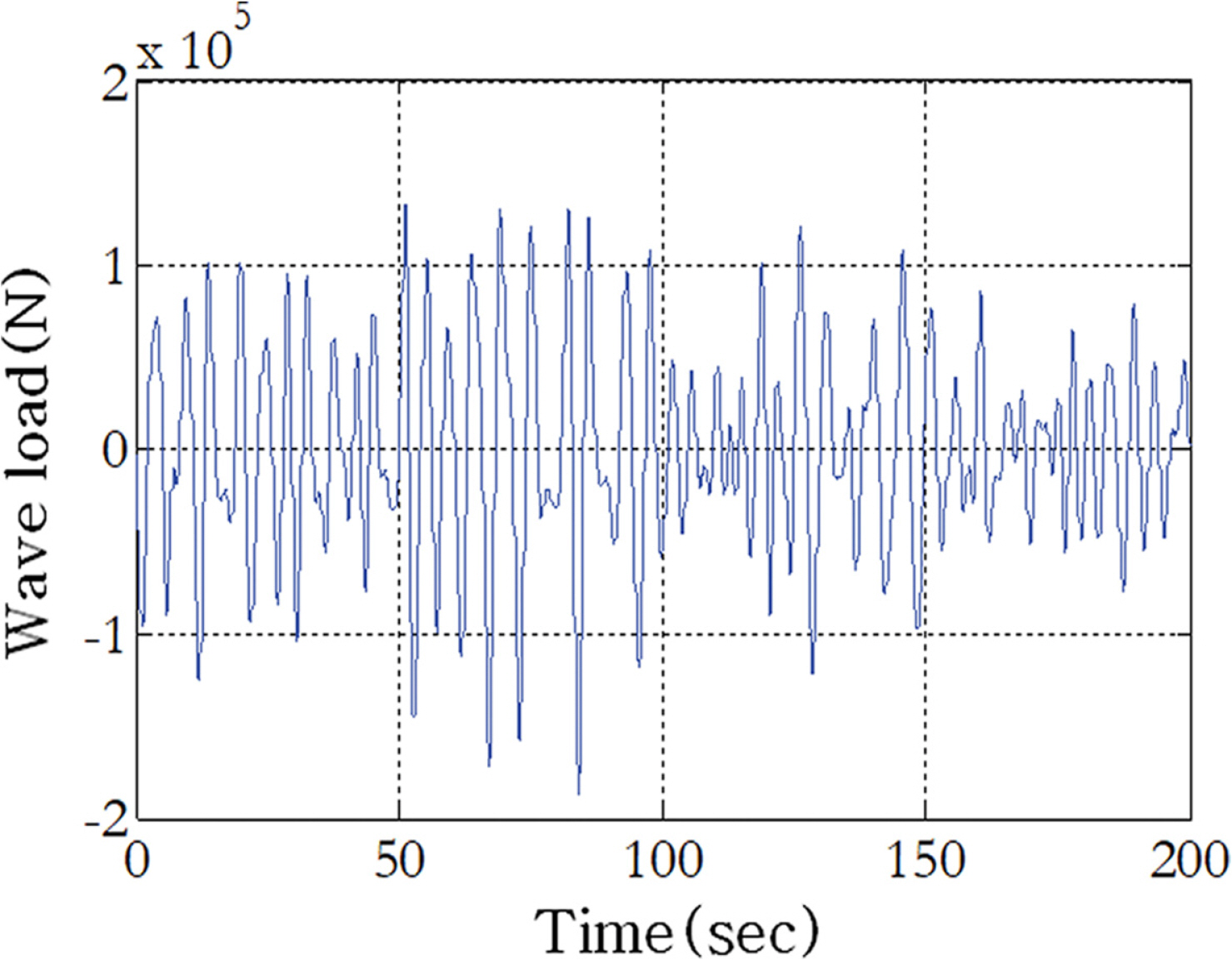
풍하중에 의한 추력의 분포를 구하기 위해 GH-Bladed (Bladed Multibody dynamics user manual, Ver. 3.85)를 사용하였다. 세굴은 정상상태에서 지속적으로 발생하는 현상이고, 해상풍력터빈은 정격풍속에서 가장 큰 추력이 발생하므로, 바람장 생성 시 3 MW 해상풍력터빈의 정격 풍속에 해당하는 설계풍속 10 m/s, 난류강도(Iref)는 0.12로 설정하였다. Fig. 3은 10분 동안 시뮬레이션을 통해 계산된 추력을 나타낸 것이다.
3.5 세굴 깊이의 확률분포 추정
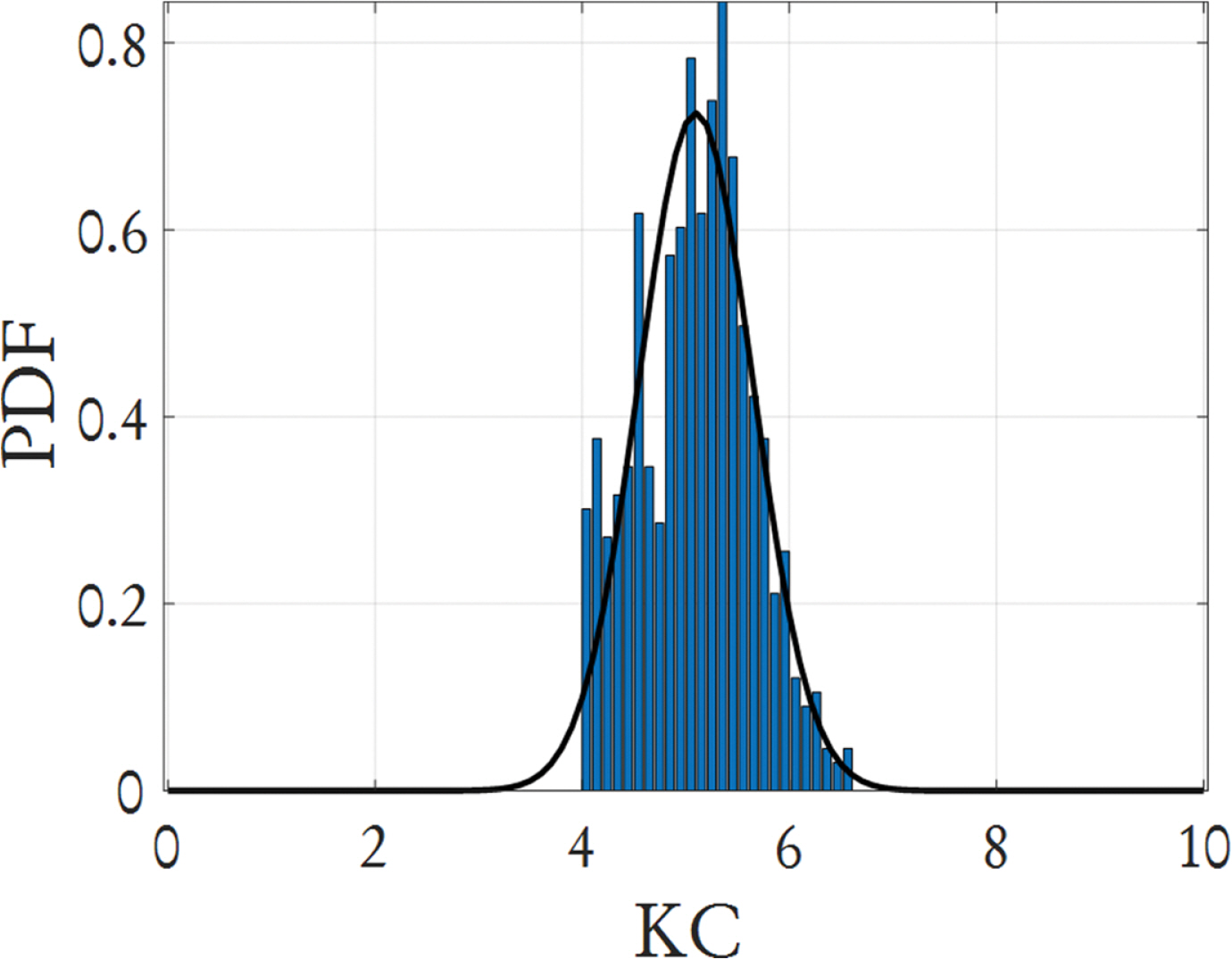
세굴위험도를 계산하기 위해서는 세굴취약도와 세굴깊이의 확률분포를 추정해야 한다. 세굴깊이의 확률분포를 추정하려면 우선적으로 KC의 확률분포를 추정해야 한다. KC의 확률분포를 추정하기 위하여 유의파고 및 유의주기의 변동성을 이용하여 KC의 값을 계산한 후 KC 값이 B보다 큰 값들만을 이용하여 KC의 확률분포를 추정하였다.
KC의 분포는 정규 분포에 적합하였으며, 평균과 표준편차는 각각 5.31과 0.52로 추정되었다. Fig. 6은 추정된 KC의 확률분포를 나타내었다.
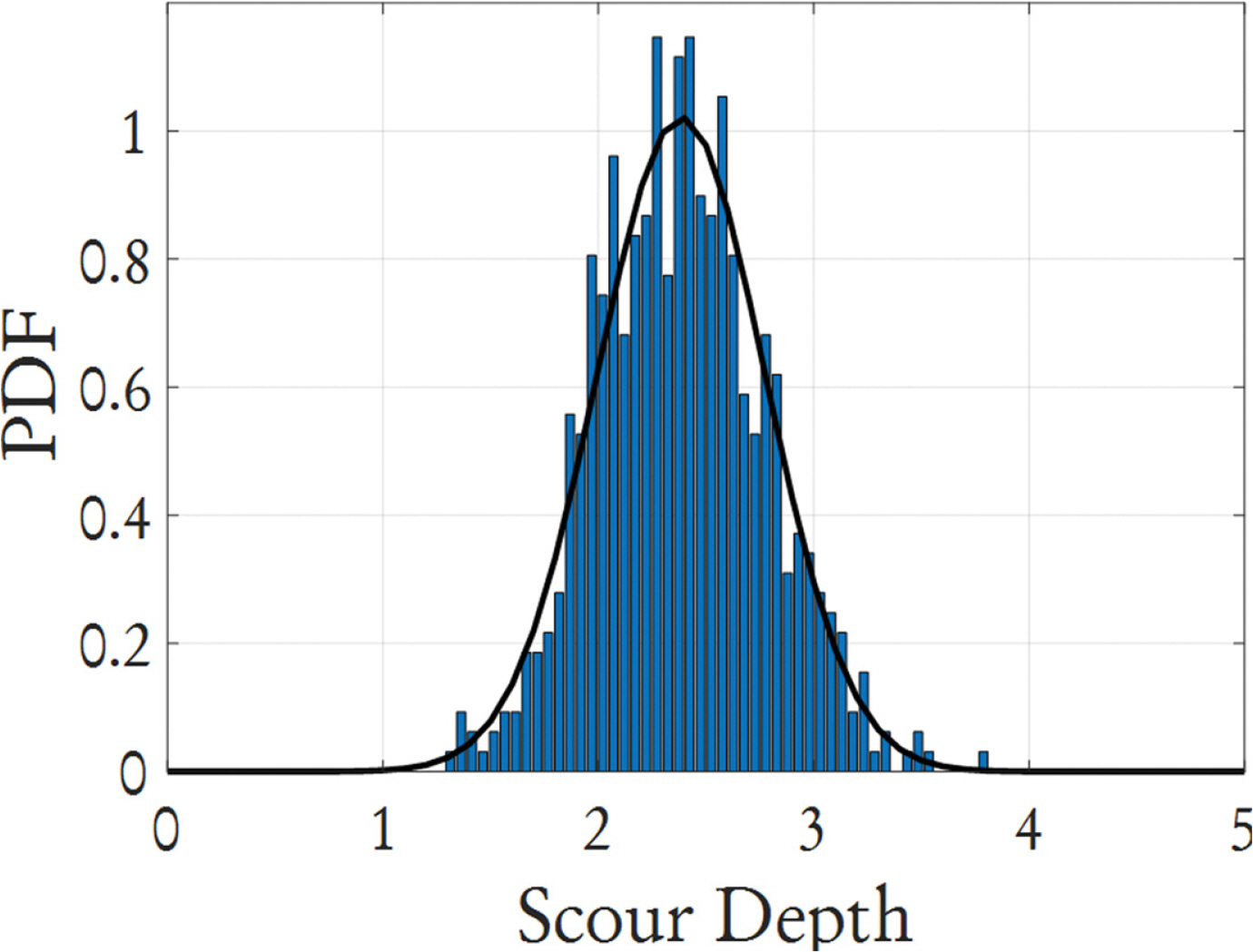
조류속의 자료는 국립 해양조사원에서 제공하는 수치조류도 2018의 자료를 이용하여 분포를 추정하였다. 각 격자점에서 2019년 1월 1일 00시 10분부터 2019년 12월 31일 23시 50분까지 1년의 자료를 이용하여 분포를 추정하였다. 조류속의 분포는 정규분포에 적합하게 추정되었으며, 각각의 평균과 표준편차는 1.34 및 0.19로 나타났다.
3.6 세굴취약도 산정
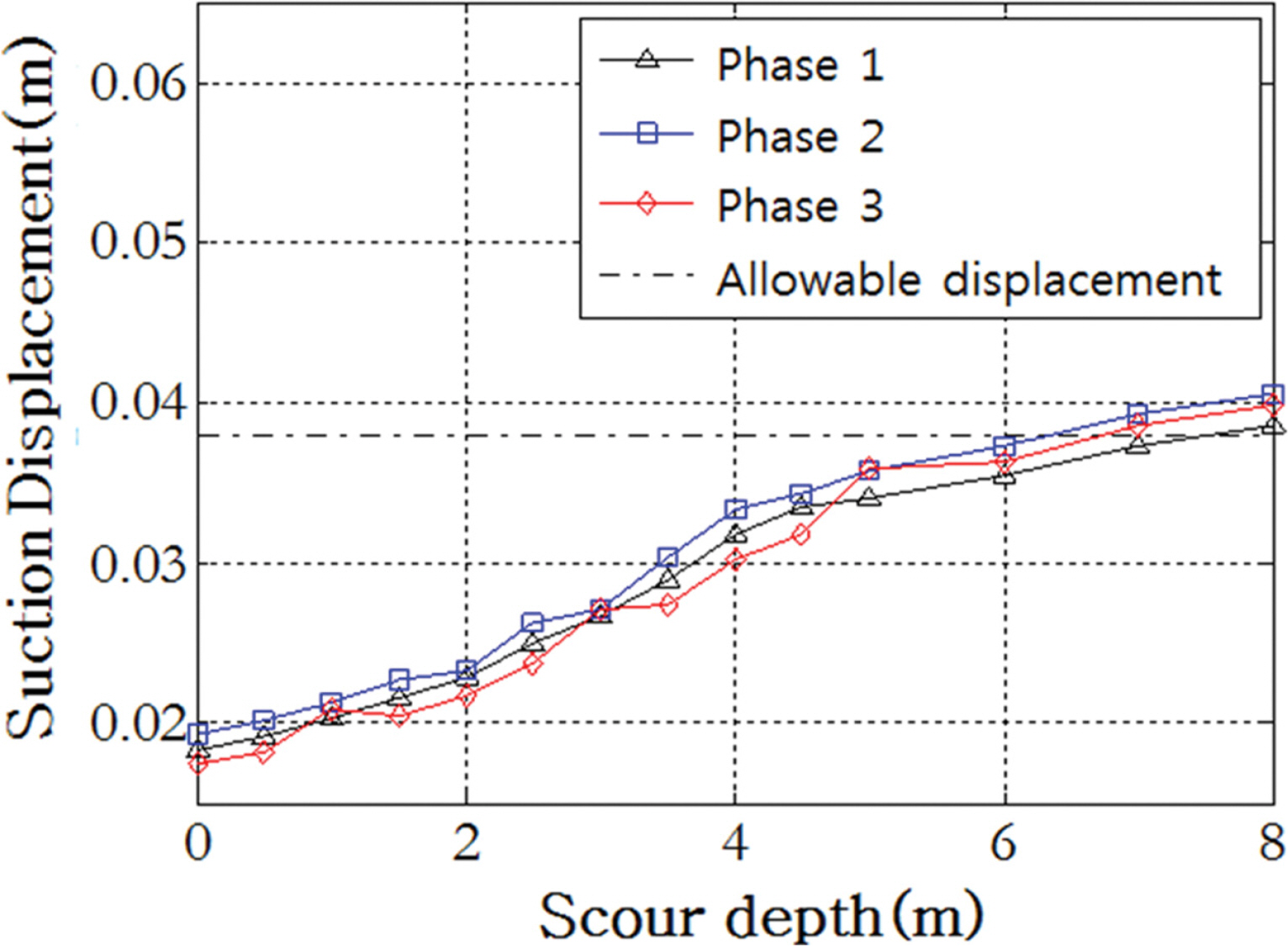
세굴취약도를 산정하기 위하여 계산된 추력과 파랑하중을 적용한 동적 변위 해석을 수행하였다. 세굴 깊이는 0~8 m까지 가정하여 해석을 수행했고, 추력은 바람장의 위상을 변경하여 총 3가지 추력에 대하여 해석을 수행하였다. 해석시간은 총 180 sec에 대하여 해석을 진행했으며, 세굴깊이와 추력 및 파랑하중을 변화하며 해석한 총 해석 case는 168개 이다. 해석한 동적 변위 결과를 Fig. 8에 나타내었다. Fig. 8의 그래프는 각각의 case에 대한 해석 결과에서 mudline 위치에서의 최대 수평변위의 값을 추출하여 도시하였으며, 그래프에서 확인할 수 있듯이 입력하중 때문에 차이가 발생하지만 최소 5.88 m 정도 세굴이 발생했을 때 변위가 허용 변위인 38 mm를 초과하는 것을 확인할 수 있었다.
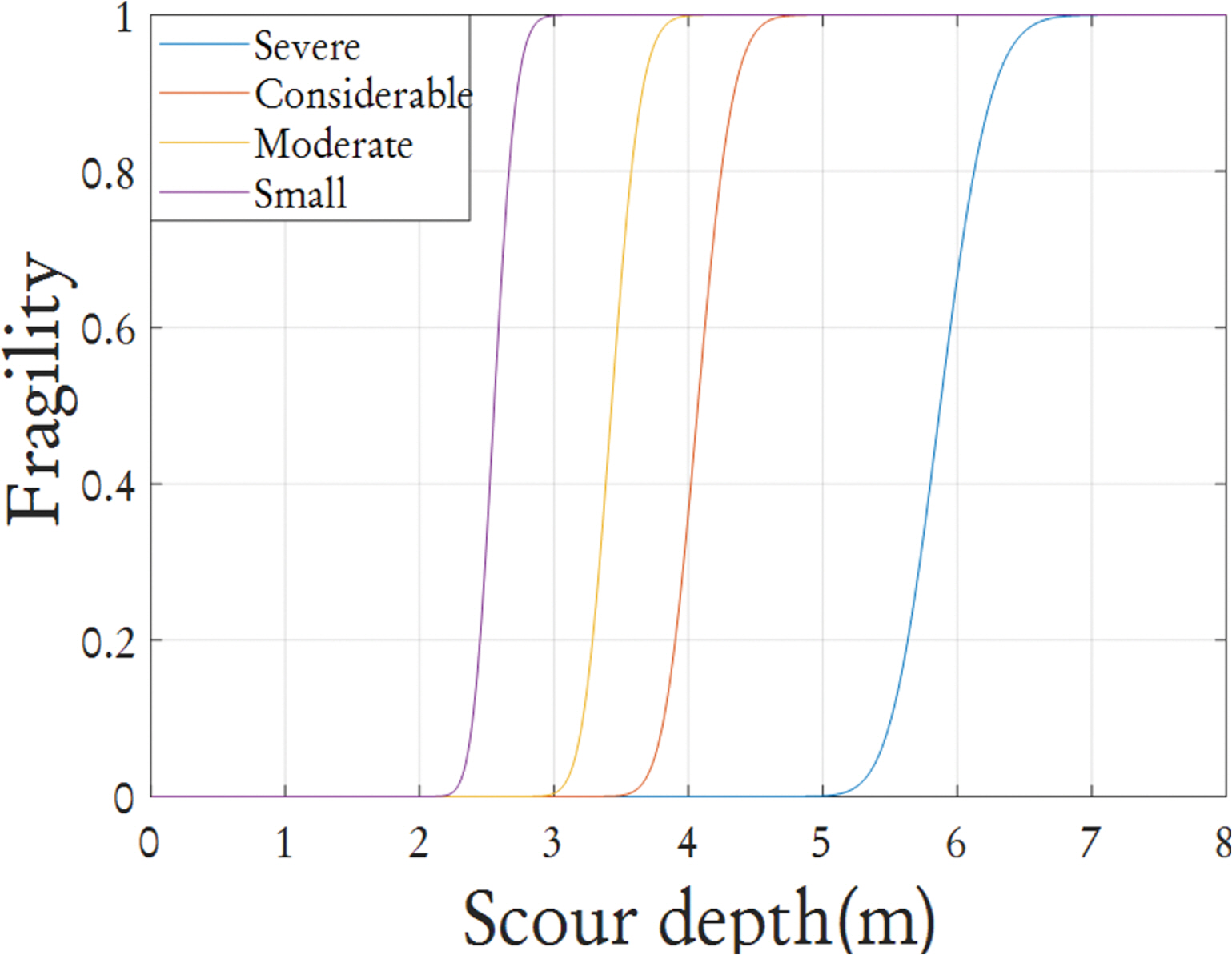
세굴에 대한 취약도를 평가하기 위하여 발생할 수 있는 손상의 정량적 정의가 필요하다. 이에 본 연구에서는 구조물기초에 적용되는 AASHTO LRFD Bridge Design Specification을 준용하여 38 mm로 결정하였다. 또한, 허용 변위의 100%, 90%, 80%, 70%에 해당하는 ‘severe’, ‘considerable’, ‘moderate’ 및 ‘small’의 네 가지 손상 수준을 정의하여 각각의 손상 수준에 해당하는 취약도를 계산하였다. Table 3 및 Fig. 9는 각각의 손상수준에 대해 계산된 취약도 결과를 나타내고 있다.
대수표준편차가 모두 0.05로 동일하게 나타난 이유는 구조해석을 진행할 때 모두 동일한 세굴 깊이에서 하중의 변동성만 고려하여 해석이 진행되었고, 하중의 변화만 있기 때문에 대수표준편차가 동일하게 나타났다. 대수표준편차가 서로 다르게 나타나려면 서로 다른 해석 깊이에서 해석을 진행하여야 다르게 나타날 것으로 판단된다.
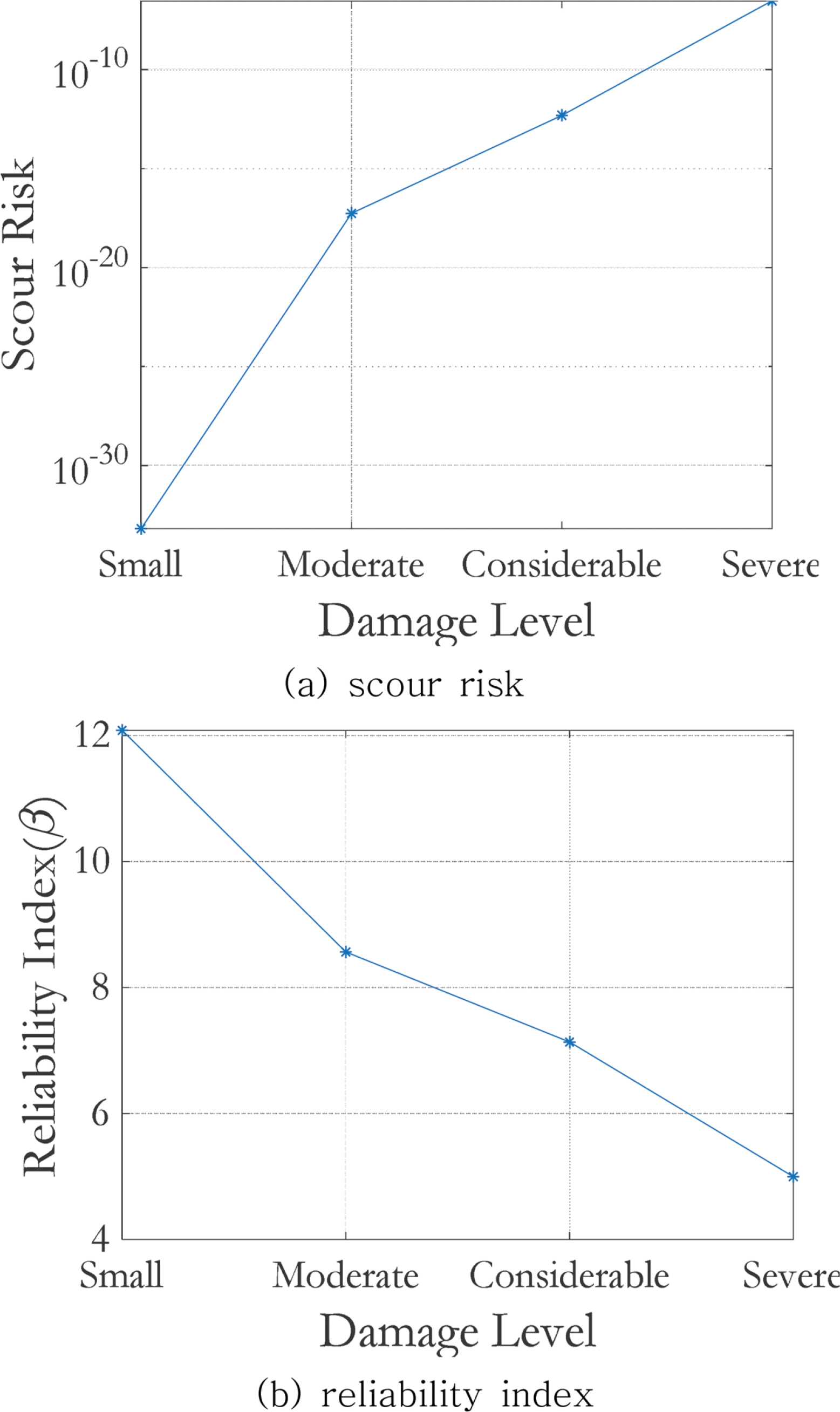
DNV에서 제시한 최대 세굴 깊이의 경우 직경의 1.3배를 고려하도록 명시되어있다. 이러한 설계기준을 적용할 경우 최대 세굴 깊이는 7.8 m가 되며, 이 경우 모든 손상수준에서 파괴가 발생된다.
4. 결 과
해상풍력터빈 지지구조물의 확률론적 설계를 위하여 세굴 위험도 평가기법을 제안하였다. 세굴 위험도 평가기법은 지진의 확률론적 평가 방법 중의 하나인 지진위험도 평가기법을 변형하여 세굴 위험도 평가 기법을 개발했으며, 세굴 취약도 곡선과 세굴 깊이의 확률분포를 결합하여 세굴 위험도 해석을 진행하였다. 지진위험도 분석기법은 구조물의 파괴를 발생시키는 위험인자를 지진의 크기, 즉, P.G.A.로 정의하며 P.G.A.가 증가할수록 구조물이 파괴될 확률이 증가한다. 하지만 세굴을 고려한 지지구조물 위험도 분석 기법은 구조물의 파괴를 발생시키는 위험인자를 세굴 깊이로 정의하여 세굴 깊이가 깊어질수록 구조물이 파괴될 확률이 증가하는 것으로 정의하였다. 동일한 하중이 구조물에 작용할 경우 세굴 깊이가 깊어질수록 구조물의 지지력은 감소하기 때문에 구조물의 파괴확률도 증가하게 되므로 세굴 취약도 및 위험도를 계산하는 방법은 타당하다고 판단된다. 또한, 사용성 평가를 위해 4단계의 손상 수준을 정의하고 각각의 손상 수준에 대한 취약도 및 위험도를 계산하였다.