1. 서 론
최근 태풍 차바, 하이선 및 바비 등의 내습으로 인하여 방파제 및 해안시설물에 크고 작은 피해가 발생한 것으로 보도되고 있다. 또한 최근 심해설계파 제원 및 산정기법이 변경되면서 구조물 설계파가 변동(상향)될 가능성이 있다. 이로 인하여 항만 및 해안 시설물 중 경사식구조물에 거치된 피복재(테트라포드 등)의 안정중량을 산정하는 파고가 증가함에 따라 기존 경사식구조물의 피복재를 보강해야 하는 필요성이 증대하고 있다. 이와 같은 경사제의 피복재 보강을 위해 기존 피복재를 제거하고 증대된 중량의 피복재를 거치하거나, 기존 피복재 상부에 고중량의 피복재를 추가로 거치하는 보강 설계가 이루어지고 있다. 그렇지만 이에 대한 체계적인 연구 및 이에 대한 성과는 아직 없는 것으로 조사된다.
경사식구조물을 설계함에 있어 경사제의 피복재 안정중량 산정은 가장 중요한 설계 요소중 하나이다. 이와 같은 경사식구조물 피복재의 안정중량을 산정하기 위한 기법으로 가장 널리 알려진 공식은 Hudson식(Hudson, 1959)과 van der Meer식(van der Meer, 1988)을 들 수 있으며, 이 식들은 항만 및 어항 설계기준에 수록되어 있다. 이외에도 피복재의 거치방법에 따른 안정성 등에 대한 연구를 수행한 사례는 많이 있다(van der Meer and Heydra, 1991; van der Meer, 1999; De Jong et al., 2004; Gürer et al., 2005; Suh and Kang, 2012; Medina et al., 2014; Min et al., 2015). 그러나 상기 연구 성과물은 신규 구조물을 설계할 때 경사제 사면에 거치되는 피복재의 안정중량을 산정하기 위한 내용이 대부분이다.
전술한 바와 같이 본 연구에서 검토하고자 하는 경사제 사면에 기설치된 피복재 상부에 추가로 피복하는 피복재의 안정중량을 산정하기 위한 연구는 현재까지 제시되어 있지 않다. 국내에서 수행된 설계사례 분석을 통해 기존 경사제를 보강하기 위해 피복재를 추가로 거치하는 대표적인 유형을 Table 1에 정리하였으며, type 2 유형의 보강설계 사례가 가장 많은 것으로 조사되었다.
본 연구에서는 피복재로 테트라포드(Tetrapod)가 거치된 기존 경사제를 대상으로 기존 피복재 상부에 추가 피복을 실시하는 조건에서 추가 피복재에 대한 안정성을 2차원 수리모형 실험을 통해 검토하였다. 먼저 추가 피복재 거치 전 일반적인 2층 피복 단면에 대한 피복재의 안정성을 확인하고, 기존 피복층 상부에 2층을 추가 피복하는 조건에 대한 안정성을 검토하였다. 또한 국내 사례를 조사하여 거치 방법에 따른 안정성을 검토하였다.
2. 수리모형실험
2.1 실험시설
수리실험은 한국건설기술연구원의 폭 1.2 m, 높이 1.5 m, 길이 50 m의 수로에서 수행되었으며, 단면수로에는 전기서보피스톤식 조파기가 설치되어 있고, 규칙파 및 불규칙파를 조파할 수 있다(Fig. 1 참조). 그리고 단면수로의 폭 1.0 m는 폭 0.8 m와 폭 0.4 m로 분할되어 있으며, 분할된 수로에서 실험 모형은 폭 0.8 m의 수로에 설치하여 제반 자료를 취득하고, 폭 0.4 m의 수로에서는 입사파의 설정 및 보정을 수행하였다. 또한 흡수식 조파를 실시하여 구조물 및 조파기에서 재반사를 최소화 하였다. 1번 파고계는 흡수식 조파, 2번과 3번 파고계는 반사계수 측정, 4번과 5번 파고계는 협수로에서 입사파의 설정 및 계측에 이용되었다. 단면수로는 전면 30 m 구간을 강화유리로 처리하여 실험장면 관찰이 용이하도록 되어 있으며, 수로 양쪽 끝 부분에는 여러 겹의 다공성 구조로 형성된 소파장치가 설치되어 있다.
2.2 실험파 조건
실험파는 Bretschneider-Mitsuyasu 스펙트럼을 적용한 불규칙파 조건을 적용하였으며, 목표 유의파고(HS, target)는 HS, target = 9 cm~20 cm 범위에서 0.5 cm 간격으로 설정하였으며, 목표 유의주기(TS, target)는 TS, target = 1.7~2.54 s 범위에서 약 0.25 sec 간격으로 설정하였다. 실험파는 구조물 설치위치에서 구조물이 설치되지 않은 상태에서 설정하였다. 구조물 설치 후 흡수식 조파를 적용하여 구조물에서의 반사파를 수로내에서 최소화하였다. 본 실험에서는 실험시 폭 0.4 m 수로의 구조물 toe 위치에서 입사파(HS 및 TS)를 상시 분석하여 안정성 분석시 입사파로 활용하였다. 여기서, HS는 유의파고, TS는 유의주기이다. 실험결과 분석시 사용된 입사파고(Hs, measured)는 Table 2에 제시된 목표 실험파를 대상으로 생성된 스펙프럼에 의하여 계측된 파고(GAGE 4번 과 5번 이용, Fig. 1 참고)를 입반사 분리하여 분석한 값이다. 구조물 설치수심(hs)은 hs = 0.5 m 조건을 적용하였다. Fig. 2는 본 실험에서 설정한 실험파 스펙트럼의 일부를 도시한 것이다.
2.3 실험 단면
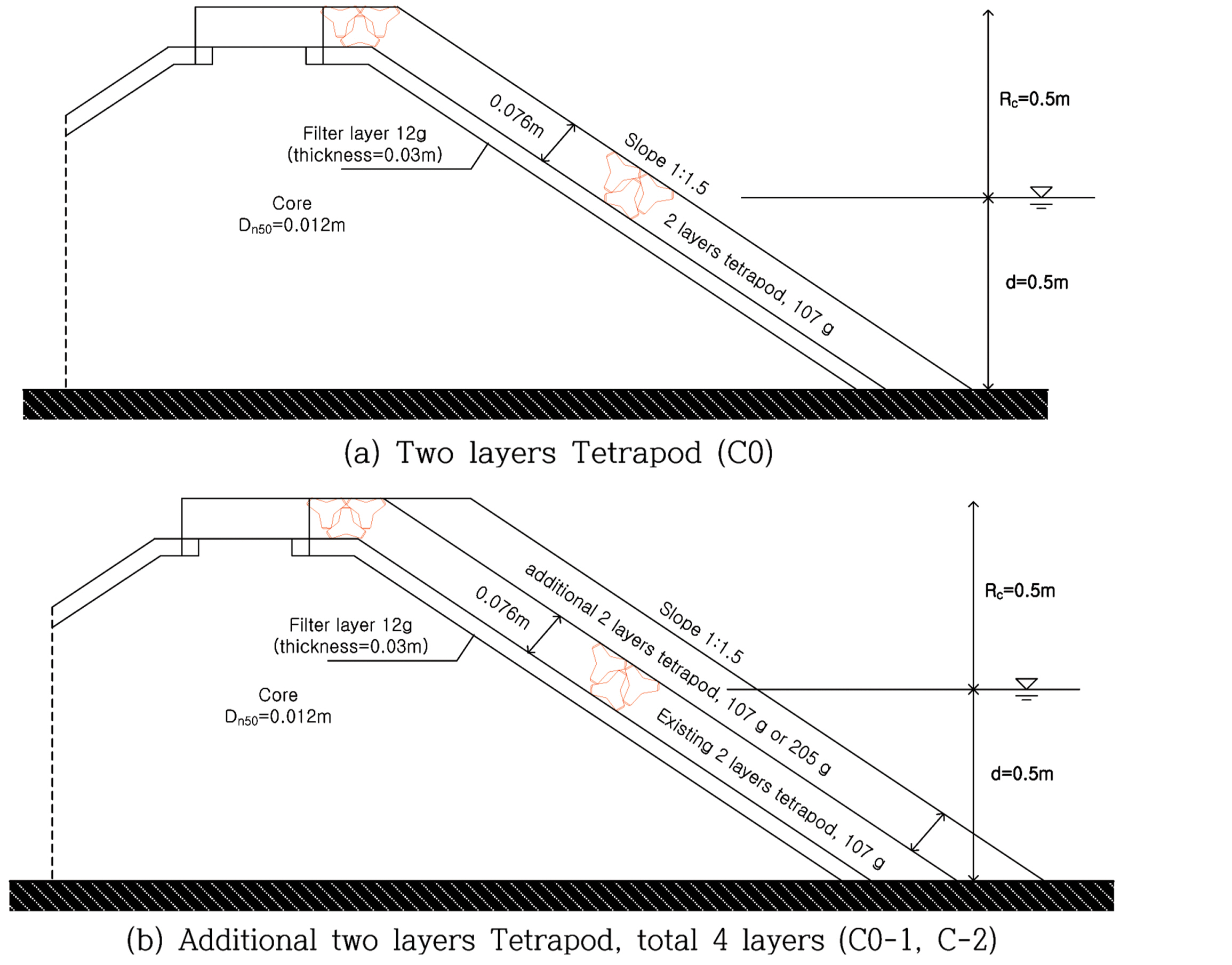
본 연구에서 검토한 실험단면은 테트라포드가 거치된 경사식 단면으로서 실험은 월파가 발생하지 않는 비월파 조건과 월파가 발생하는 월파조건을 적용하였다. 본 연구에 적용된 실험 단면 모식도와 단면 조건을 요약하면 Table 3 및 Table 4와 같다.
월파가 발생하지 않는 비월파 조건의 경우, 1:1.5의 경사면 상부에 테트라포드가 2층 피복되어 있는 조건(C0, Table 3(a) 참조)과 기존 2층 피복층 상부에 추가로 2층을 피복하여 총 4층의 피복재가 거치된 단면(C0-1과 C0-2, Tab1e 3(b) 참조)을 대상으로 하였다. 테트라포드가 2층 피복된 단면(Table 3(a) 참조)은 Hudson식 및 기존 연구에서 제시된 테트라포드의 안정계수의 값을 검증 및 비교하기 위하여 수행되었다. 그리고 기존 피복층 상부에 추가로 2층이 피복되어 총 4층이 거치된 단면(Table 3(b) 참조)을 이용하여 추가 피복재의 안정성을 검토하였다.
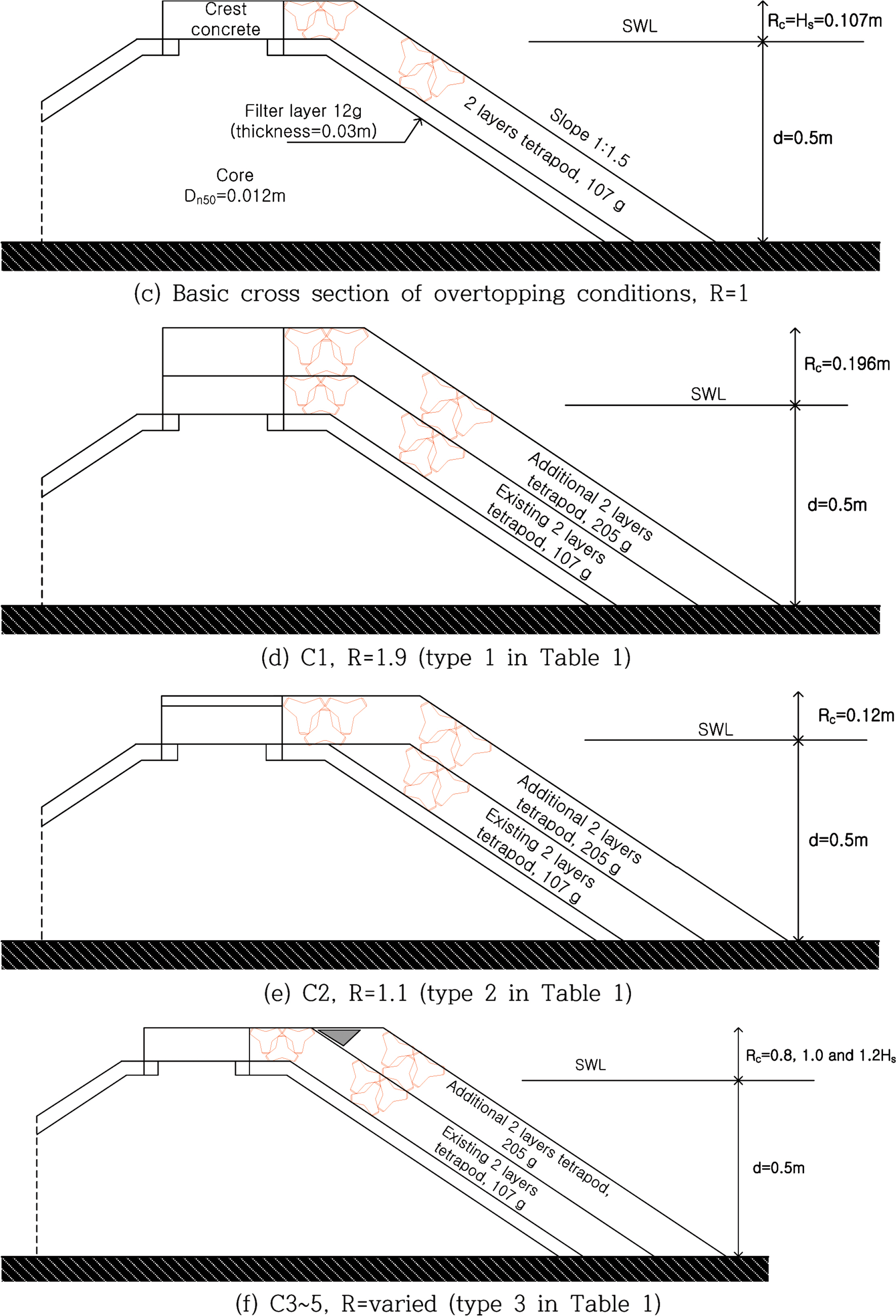
월파가 발생하는 조건의 경우에는 Table 1의 기존 경사제 보강사례에 제시된 단면형상에 대하여 안정성 실험을 검토하였다. 월파조건의 경우, Table 3(c)의 기본 단면(basic cross section)을 기준으로 상치콘크리트와 경사면 피복재를 모두 보강한 C1(Table 3(d) 참조)과 C2(Table 3(e) 참조)를 대상으로 추가 피복재의 안정성을 검토하였다. 이는 Table 1의 type 1 및 type 2와 유사한 단면이다. 또한 Table 1의 type 3의 단면 형상에 대해서는 C3~C5의 단면(Table 3(f) 참조)을 적용하였다. 이때 구조물의 마루높이는 하부 피복재의 설계파고 대비 0.8배, 1배 및 1.2배이다. 이들은 상대여유고(R = RC/HS)가 R = 0.8, 1 및 1.2인 조건을 의미한다. 또한 C3~C5의 단면 적용시 피복재의 크기(부피) 및 거치 방법으로 인해 피복재 어깨 구간에 형성되는 역삼각형 형태의 빈 공간의 유무에 따른 피복재의 안정성을 검토하였다.
본 실험에서 피복재(테트라포드)의 거치방법은 정적거치를 적용하였다. Table 3에서 기존 피복재는 W = 107 g/ea의 테트라포드이다. Hudson식을 이용하여 계산된 107 g/ea 테트라포드의 안정파고는 사면경사 1:1.5 및 비쇄파 조건(KD = 8) 적용시 HS = 10.7 cm이다. 추가 피복재로는 기존 경사제에 거치된 피복재(테트라포드)의 중량(W, 107 g/ea)과 동일한 중량(W)과 205 g/ea(약 2 W)의 테트라포드를 적용하였다. 107 g/ea 테트라포드의 안정파고 계산 방식과 동일하게 205 g/ea 테트라포드의 안정파고를 계산하면 HS = 13.3 cm이다. 기존 피복재 하부에는 중간피복재로 12 g/ea의 골재, 제체사석으로 Dn50 = 1.2 cm의 골재를 설치하였다.
3. 실험결과
3.1 실험결과 분석
일반적으로 피복재의 안정검토는 안정수(NS)를 이용하여 분석을 하고 있으며, 안정수는 식(1)과 같이 표현된다.
식(1)에서 ∆ = (Sr - 1)이고, Dn은 피복재의 공칭길이이며, Dn = (M/ρr)1/3이다. ρr은 피복재의 밀도, Sr은 피복재의 해수에 대한 비중이다. 위 식에 근거한 Hudson식은 식(2)와 같다.
본 연구에서는 콘크리트 이형블록의 안정성 검토시 적용되는 Nod를 기준으로 피해 및 안정수를 계산하였다. Nod는 상대실험구간(= B/Dn) 내에서 이탈된 피복재의 개수(N)를 의미한다(Nod = N/(B/Dn)). B는 안정성 평가를 위한 유효 실험 계측 구간의 폭이다. 금번 안정성 실험에서는 수조 양측면에 거치되는 테트라포드를 쇠사슬(rope)로 고정시켜 이탈이 발생하지 않도록 하였으며, B의 계산 시 수조 양쪽 측면에 거치되는 테트라포드의 폭 만큼을 제외하였다.
테트라포드의 경우 초기피해(start of damage)를 Nod = 0.2~0.5 범위로 제시하고 있으며(CIRIA et al., 2007; van der Meer, 1999), 본 연구에서는 1,000파를 연속조파 한 후 Nod = 0.3을 기준으로 안정성을 검토하였다.
3.2 비월파 조건 실험결과
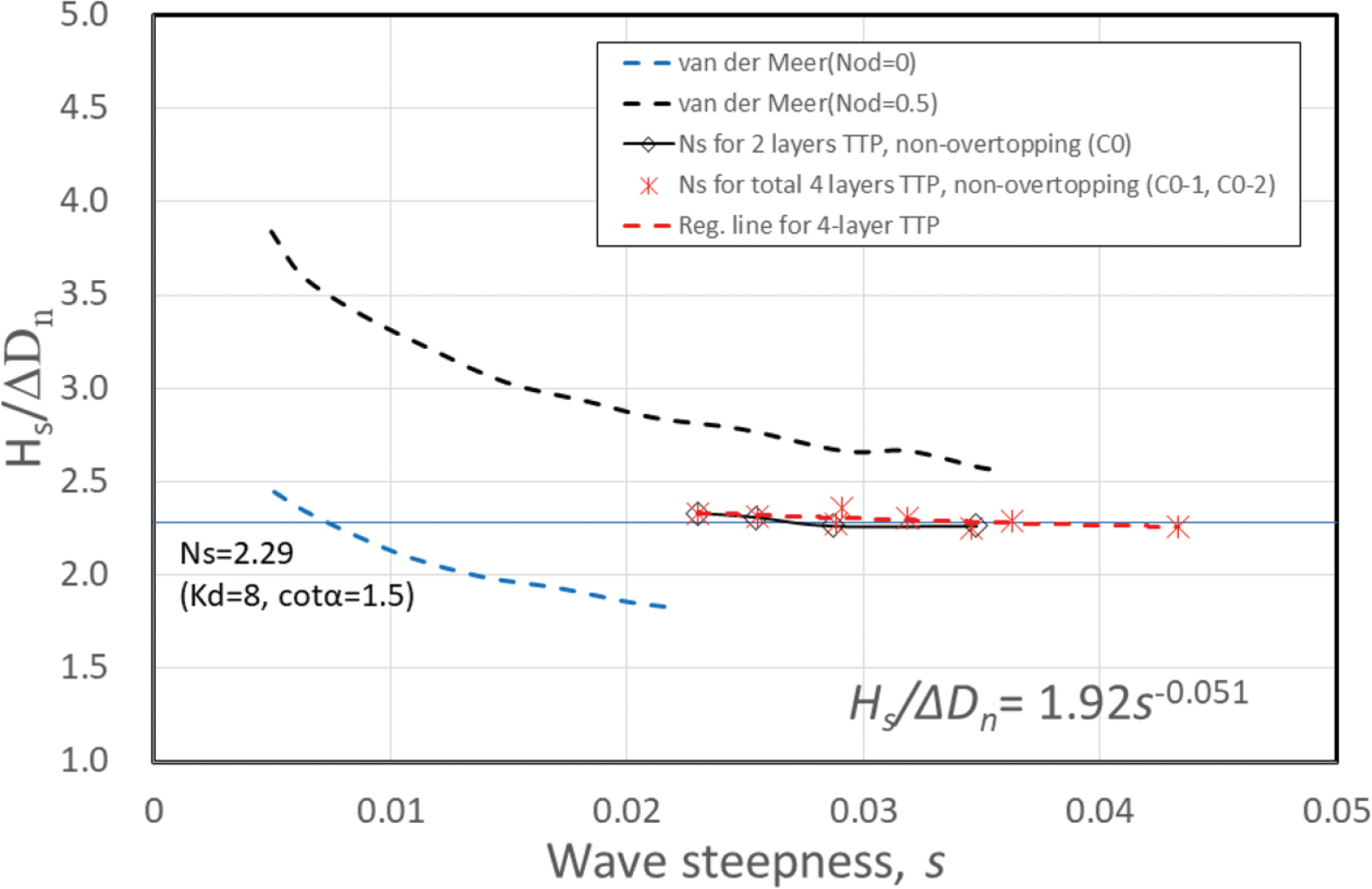
Table 3 및 Table 4의 실험 단면 조건에서 비월파 조건인 C0, C0-1 및 C0-2 단면을 대상으로 안정성 실험결과를 Table 5 및 Fig. 3에 제시하였다. 일반적인 테트라포드 2층 피복 조건에 해당하는 Table 3(a)의 단면(C0)에 대한 KD는 주기조건에 따라 일부 차이는 있으며 KD = 7.8~8.4 범위로 산정되었다. 이는 Min et al.(2015) 결과와 유사하다. Min et al.(2015)에서는 테트라포드의 거치방법에 따른 KD를 제시하였고 거치 방법에 따라 평균 7.50 및 7.28이 제시되어 있다. Table 3(b)와 같은 조건에 대한 추가 피복재(C0-1 및 C0-2 조건)에 대한 안정계수를 비교해 보면 기존 2층 피복시(C0)에 비해 안정성이 다소 증가하는 것을 알 수 있으나 그 차이는 크지 않다. 주기별로 차이는 있으나 KD = 8을 기준으로 본 실험에서 적용한 실험조건 중 최대 약 10% 증가한 것을 볼 수 있다.
본 실험에서 적용한 실험조건 범위는 파형경사(s) 기준 s = 0.02~0.04 범위 조건으로서 파형경사에 따른 안정수(Ns)는 큰 차이가 없는 것을 알 수 있다. 이는 Hanzawa et al.(1996)이 제시한 결과와 동일한 것이다.
Fig. 3에는 van der Meer식의 Nod = 0과 Nod = 0.5인 결과를 같이 제시하였으며, 금회 실험결과는 중간에 위치하는 것을 확인할 수 있다. 그리고 테트라포드 KD = 8에 대한 안정수는 Ns = 2.29이다.
3.3 월파 조건 실험결과
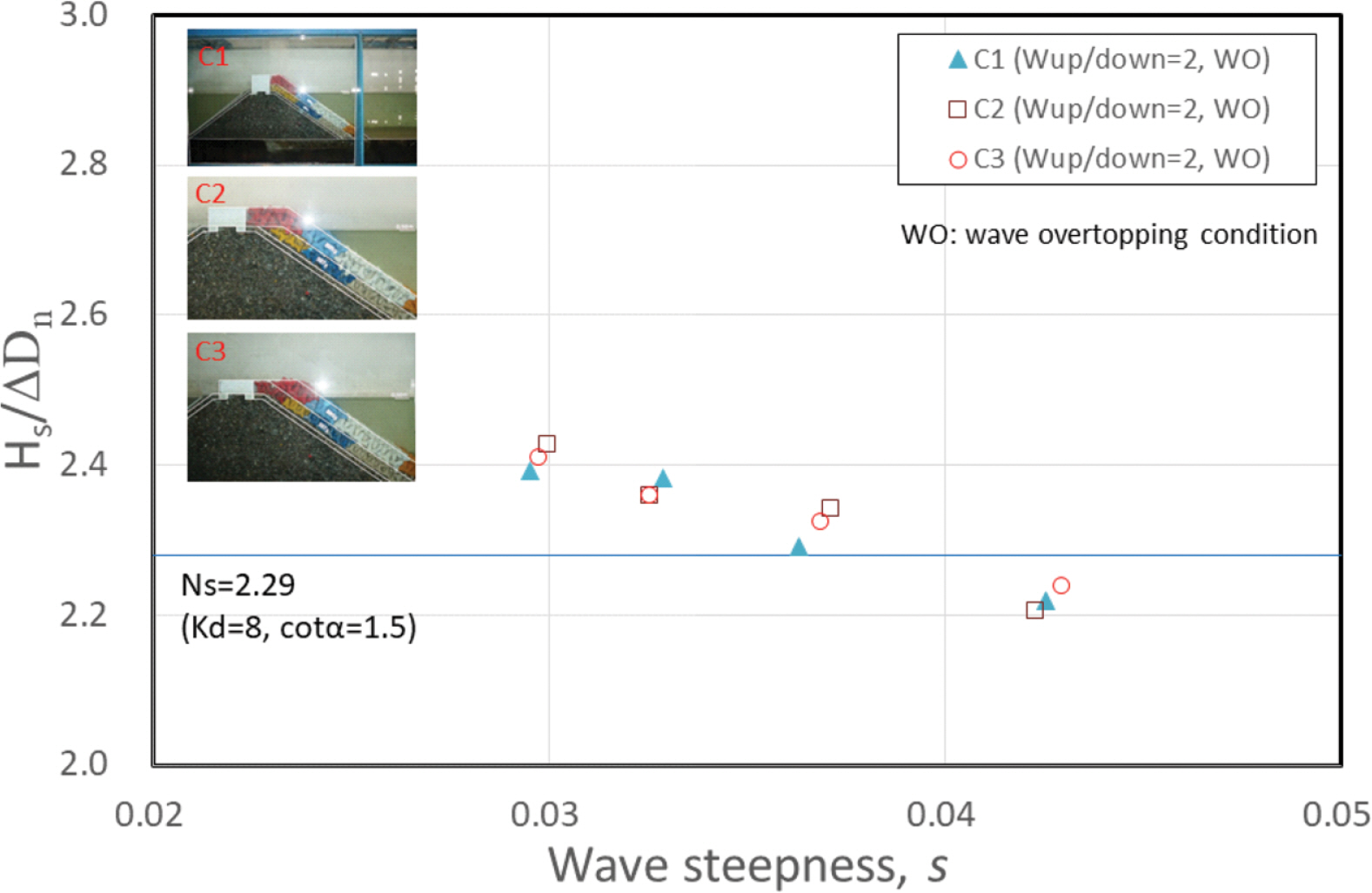
첫째로 Table 1의 type 1, 2 및 3에 해당하는 월파조건 C1, C2 및 C3에 대한 안정성을 분석하였다. 실험결과에 의하면 거치 방법(실험안) 별로 큰 차이는 없는 것을 확인 할 수 있다(Fig. 4 참조). C1~C3에 대한 안정계수 실험결과는 Table 6에 제시되어 있다.
둘째로 Table 1의 type 3에 해당하는 단면과 같은 추가 피복재 거치시 피복재 어깨 구간에서 발생할 수 있는 역삼각형 형태의 빈공간의 유무에 따른 피복재의 안정성을 검토하였다. Table 3(f)에서와 같이 도면상에서는 어깨부에 수평으로 피복재 거치 높이가 표현되지만, 실제 피복재(테트라포드)가 갖고 있는 부피로 인하여 도면과 같이 거치하는 것이 쉽지가 않다. 즉, 역삼각형 형태의 빈공간이 생기거나 계획 마루높이보다 일부 돌출되어 피복재가 거치될 수 있다.
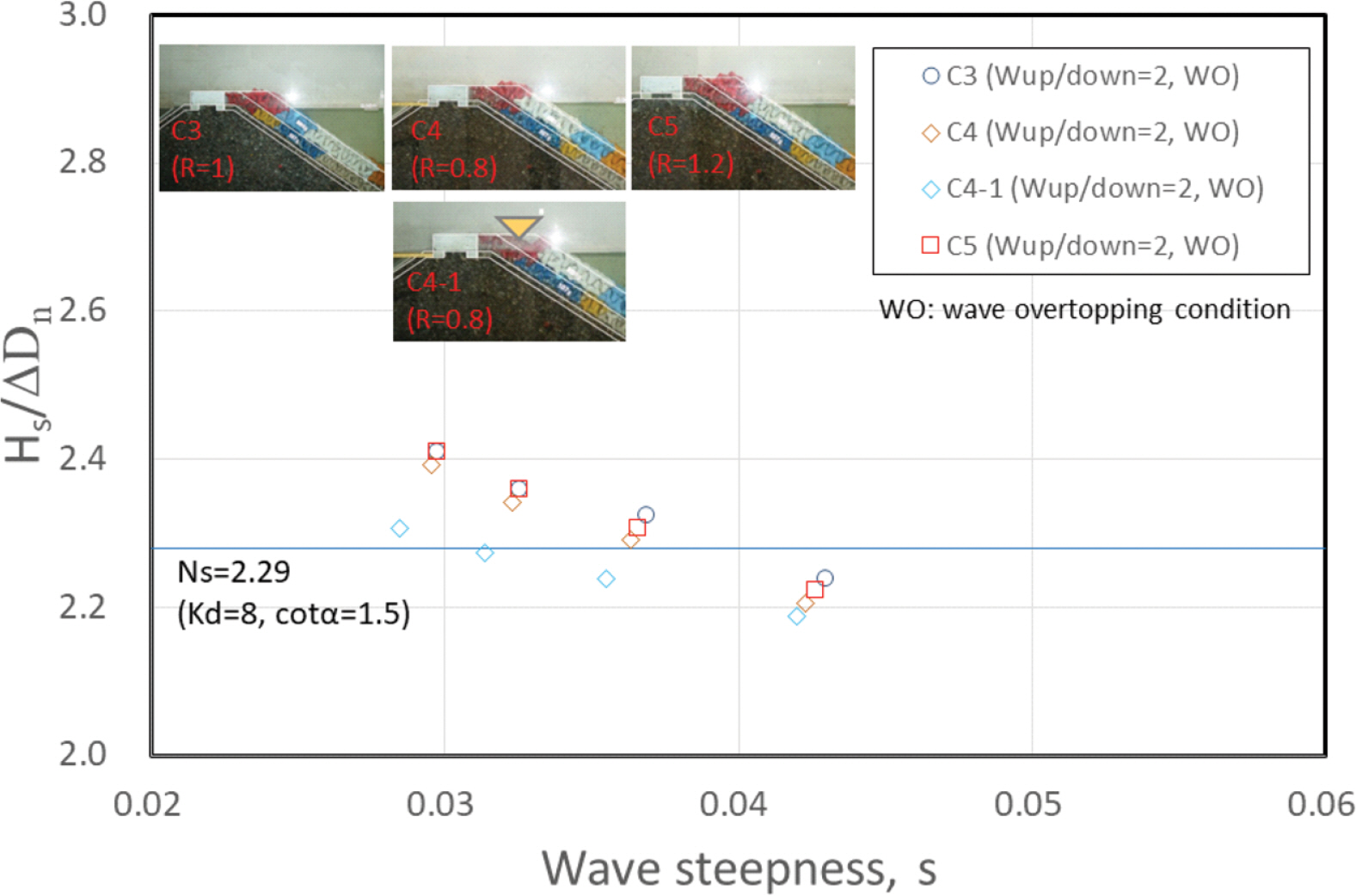
또한 상대여유고를 변경시켜 마루높이의 영향을 검토하였다. C3~C5 단면의 상치콘크리트 마루높이는 기존 하부 피복재의 안정중량을 만족하는 설계파고의 1배(R = 1, C3), 0.8배(R = 0.8, C4 및 C4-1), 1.2배(R = 1.2, C5)이다. C3, C4 및 C5는 피복재 어깨부분의 빈공간이 최대한 생기지 않도록 거치한 단면으로서 테트라포드 일부가 돌출되어 있다. C4-1은 역삼각형 형태의 빈공간이 있는 조건이다.
C3~C5의 실험결과에 의하면 마루높이가 상대적으로 낮은 조건에서 피복재의 안정성이 근소하게 불리한 것을 알 수 있다. C4-1의 경우에는 피복재 사면을 처오른 파랑이 어깨부 빈공간(피복재가 거치되지 않은 역삼각형 공간)에 영향을 주기 때문에 피복재의 피해가 더 크게 발생하였으며, 이로 인하여 안정성이 다른 조건에 비하여 작게 나타난 것을 볼 수 있다(Fig. 5 참조).
월파 조건 C3~C5에 해당하는 안정계수 실험결과는 Table 6에 제시하였다.
4. 결 론
최근 기후변화 등으로 인해 설계파가 상향되는 추세이며, 이에 따라 기존 경사제 사면에 거치된 피복재의 보강을 위하여 기존 사면 위에 추가 피복재를 거치하는 설계가 진행되고 있다. 그러나 이와 같은 설계 방식에 대한 피복재의 안정계수 산정법은 아직 제시되어 있지 않다. 본 연구에서는 주 피복재가 테트라포드인 경우, 추가 피복재(테트라포드)의 안정성을 실험적으로 검토하였다. 실험결과에 의하면, 기존 피복재가 정적이고 사면경사의 변화가 없는 경우로 가정할 경우에 추가로 거치되는 피복재의 안정성은 Hudson식에서 제시하고 있는 안정계수(KD = 8)에 비해 주기별로 일부 차이가 있으나 실험조건 내에서 최대 10% 증가한 것을 확인 할 수 있다(비월파 조건). 월파조건에서 피복재 거치방법(C1, C2 및 C3)에 따른 안정성의 차이는 크지 않은 것으로 나타났다. 상대적으로 마루높이가 낮은 경우에는 내습파가 피복재 마루부에 영향을 많이 주기 때문에 안정성이 상대적으로 낮은 것으로 나타났다. 피복재 거치 방법에 따라 추가 피복재 어깨 부분에 빈공간이 생성되는 경우에는 피복재의 안정성이 감소하는 것을 확인하였다. 이는 도면상에서는 피복재 어깨부가 수평으로 빈 공간이 없는 것으로 작성 되지만, 실제 콘크리트 이형블록이 갖는 체적으로 인하여 피복재 어깨에 공간이 발생할 수 있다. 따라서 피복재 어깨 부분에 거치되는 피복재의 안정성을 확보하기 위해서는 최대한 빈공간이 발생하지 않도록 피복재를 거치해야 할 것으로 판단된다.
본 연구에서는 기존 피복재 사면의 변화가 크지 않고, 피복재가 정적으로 거치된 조건을 대상으로 추가 피복재의 안정성을 검토하였다. 그렇지만 실제 현장에서는 고파랑에 의하여 기존 피복재의 변형이 발생하였을 가능성이 크므로 기존 피복재가 난적으로 거치(흐트러진 조건)된 조건에 대한 연구가 필요하며, 이에 대해서는 추후 연구를 통하여 제시할 계획이다.