1. 서 론
중력외파(infragravity waves)는 바람에 의해서 발생되는 단주기 파 보다 주파수가 낮은 표면파로서 외중력파 또는 장주기 중력파로 불리기도 한다. 단주기 파는 0.04 Hz~1.0 Hz의 주파수를 갖는 반면에 중력외파는 0.004 Hz~0.04 Hz의 주파수에 해당한다. 중력외파는 Munk(1949)에 의해서 처음으로 관측되었으며, 발생 원리는 외해로부터 전파하는 단주기 파들의 2차 비선형 상호작용에 의해서 파군 내에 장주기 파가 만들어진다는 구속파(bound wave)이론(Biesel, 1952; Longuet-Higgins and Stewart, 1962)과 해안으로 전파하는 파랑의 파고 차이 때문에 시간차를 두고 쇄파 점이 변하면서 쇄파 에너지의 전달에 의해서 발생한다는 자유파(free waves)이론 (Symonds et al., 1982)이 있다.
중력외파는 연안의 동수역학, 지형변동, 연안사주와 제방 붕괴 등에 상당한 기여를 하고, 항내에서는 수면진동을 발달시키는 원인이 된다(Okihiro et al., 1993). 중형 항만의 고유진동 주파수는 중력외파의 주파수범위 안에 속하므로 이들 항만에 중력외파가 전파되면 공진현상을 일으켜서 항내 수면진동의 진폭이 더욱 커진다. 특히 계류된 중·대형 선박은 주기 1분~수분의 고유진동 주파수를 가지고 있으므로 이와 유사한 중력외파가 내습하면 선박의 동요를 더욱 증폭시킬 수 있다.
중력외파에 대한 연구는 1950년대부터 현장관측 및 이론적인 연구가 진행되어 왔으며 1990년대 이후 관련 연구가 급격히 증가하고 있다(Bertin et al., 2018). 국내에서는 구속 파의 전파 특성을 해석한 연구(Jeong et al., 1997), 관측 자료를 통하여 폭풍 파와 저중력파의 상호관계를 검토한 연구(Jeong et al., 2001a), 전달함수 모형을 이용한 항 내∙외 중력외파의 특성을 분석한 연구(Cho et al., 2014), 현장관측을 통하여 이안소파잠제의 중력파 및 중력외파의 저감 효과를 검토한 연구(Jeong et al., 2018) 등이 있다.
장주기 파로 인한 항내 수면진동의 저감 방법에 대한 연구는 항만의 기하학적 평면형상을 변화시켜서 파랑에너지를 차단하거나 첨두 주파수를 이동시키는 방법(Nakamura et al., 1996; Poon et al., 1998; Lee et al., 2012; Thotagamuwage, 2014; Diaz-Hernandez et al., 2016), 항내 안벽의 일부 구역을 파랑에너지흡수 구조형식의 구조물을 설치하여 장주기파의 에너지를 흡수하고 수면진동의 진폭을 낮추는 방법(Hiraishi et al., 2009; Tai et al., 2008; Kwak et al., 2008; Gonzalez-Escriva and Medina, 2012; Gonzalez-Escriva et al., 2018), 계류로프나 방충재의 탄성계수를 변경하여 선박과 계류장치의 고유진동 주파수를 변화시키는 방법(Shiraishi et al., 1995; van der Molen et al., 2016), 외해 관측시설 및 경험식을 이용하여 장주기파의 내습을 미리 예보하는 경보시스템 방법(Suganuma et al., 1995), 항내 수역 또는 항 입구의 일부 수역을 준설하여 수심을 증가시키고 장주기파의 에너지를 분산시키는 방법(Jeong et al., 2001b, 2002) 등이 있다. 항 외측에 방파제를 설치하여 장주기 파의 에너지를 차단하는 방법은 기하학적 형상에 따라서는 항만의 폐쇄성을 더욱 심화시키고 항내에서 수면진동이 감소하지 않을 수 있으므로 항내에 파랑에너지흡수 구조물을 동시에 설치하여 장주기 파의 반사율을 낮추는 것이 효과적이다.
최근에는 항내 수질개선과 해수교환을 촉진시키기 위해서 투과방파제를 설치하는 항만이 증가하고 있다. 투과방파제는 파의 주기가 길어지면 투과율이 증가하므로 장주기 파 대책으로는 적절하지 않다고 생각할 수 있다. 만일 동해안과 같이 파랑 작용이 활발하여 중력외파의 항내 전파가 빈번하고 조석 흐름이 아주 작아서 해수교환이 어려운 항만에서 투과방파제를 이용하여 중력외파의 항내 수면진동을 저감시킬 수 있다면 항내 수질개선과 수면진동 저감을 위한 매우 좋은 방법이 될 수 있을 것이다.
본 연구는 장주기 파의 항내 수면진동 대책과 수질 문제를 동시에 고려하기 위하여 투과방파제를 활용하는 수면진동 저감 방법을 묵호항에 적용하고 저감 효과를 검토한 것이다. 여기서는 5년간의 장기 연속파랑관측자료를 분석하여 묵호 수역의 중력외파를 제시한다. 그리고 본 연구에서는 중력외파에 대한 투과파 검증 계산을 실시하여 투과율 차이에 따른 구조물 배후의 파랑장 변화를 검토하고 적정 투과율을 파악한다. 또한 저감 목표 주기는 중력외파의 항내 수면진동 현상을 해석하여 결정하고, 저감 방법들은 투과제를 이용한 여러 가지의 방법을 설정한다. 저감 방법의 효과는 진폭응답곡선을 분석하고 진폭의 감소율을 산정하여 비교한다.
2. 장기 파랑관측자료 분석
연구대상해역은 한국해양과학기술원에서 묵호항 전면의 수심 14.0 m 위치에 수압식 파고계를 설치하여 연속 파랑관측을 실시하고 있는 수역이다. 본 연구에서는 2013년 8월부터 2018년 1월까지의 약 5년간 장기 파랑관측 자료를 분석하여 묵호항 전면의 중력외파 성분을 추출하였다.
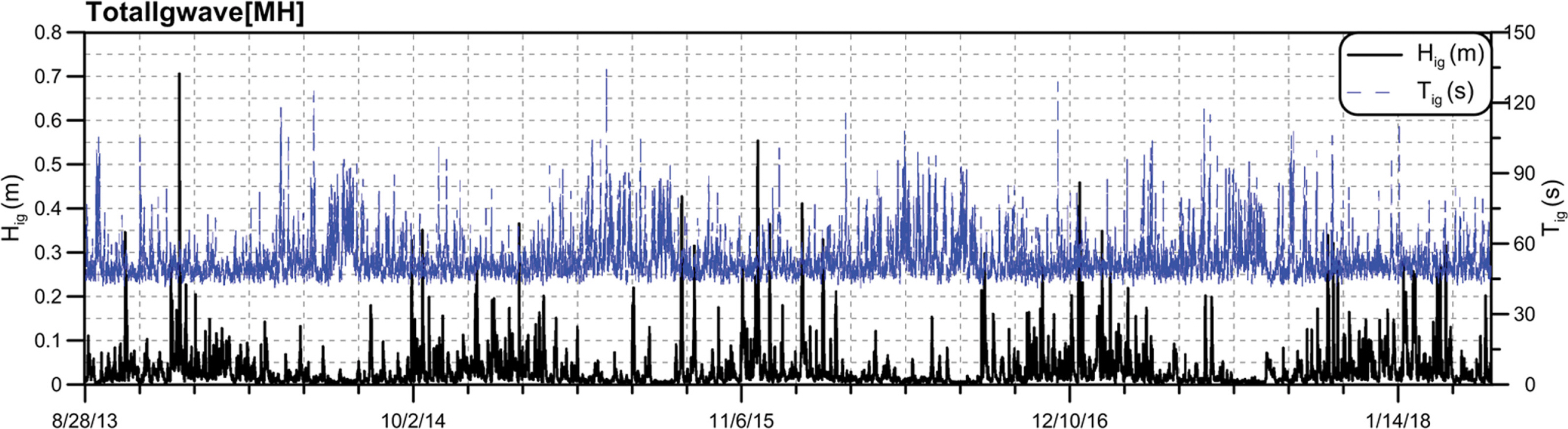
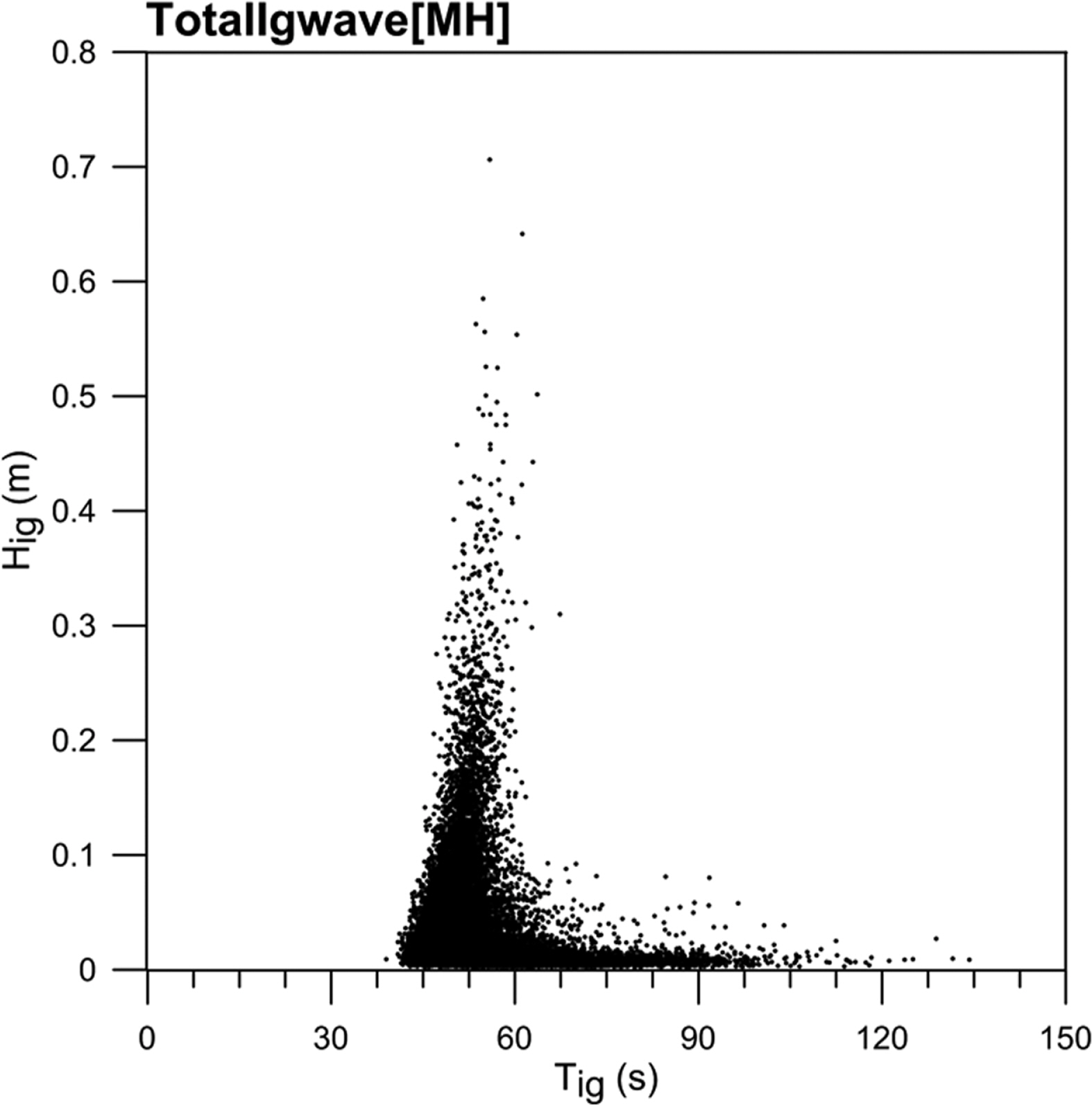
묵호항 전면 수역의 중력외파는 분석기간 동안 시계열로 표시하면 Fig. 1과 같다. 그림에서 검정색 실선은 중력외파의 파고(Hig)로서 0.01 m~0.70 m 범위를 갖으며 겨울철에 상대적으로 큰 파고를 나타낸다. 분석 기간 중에서 가장 큰 파고는 2013년 겨울에 관측된 0.7 m이었다. 그리고 파랑색 실선은 중력외파의 주기(Tig)로서 40 s~130 s의 범위로 분포한다. 또한 분석기간 동안의 중력외파 성분을 산포도로 나타내면 Fig. 2와 같다. 묵호항의 중력외파는 주기 40 s~70 s 사이에 집중 분포되어 있은 것을 알 수 있으며 파고는 0.1 m 이하에 주로 분포하고 있다.
중력외파의 파고-주기별 출현율을 정리하면 Table 1과 같다. 주기는 35 s~50 s에서 45%, 50 s~65 s에서 47%의 출현율을 나타내고 있으며, 파고는 0.1 m 이하의 파랑이 분석 자료의 94% 출현율을 보이고 있다. 따라서 묵호항 전면의 중력외파는 주기 35 s~65 s, 파고 0.1 m 이하의 성분이 전체 분석자료의 94%를 차지하고 있음을 알 수 있다.
묵호 해역의 파랑관측은 수압식 파고계를 사용하므로 파향 정보를 확인할 수 없다. 따라서 본 연구에서는 묵호에서 가장 근접한 강릉의 파향 자료를 참고하였다. 파랑은 N, NNE, NE, ENE, E, ESE, SE의 7개 방향에서 전파하였고 파랑 출현율이 가강 높은 방향은 NE 방향으로 전체 파랑의 22%를 차지하였다(Jeong et al., 2016).
3. 항내 수면진동 해석
3.1 파랑모델
본 연구에서 사용한 파랑수치모델은 분산특성을 개선한 MIKE21의 Boussinesq Wave Model(Madsen et al., 1997)로서 모의 가능한 최대수심은 심해파장의 1/2(h/L0 ≈ 0.5)이다. 본 모델은 평면 2차원 파동장의 변수들을 space-staggered rectangular grid로 표시하고 유한차분법을 이용하여 음해법으로 푼다. 재현 가능한 현상은 파랑의 천수, 굴절, 회절, 쇄파, 바닥마찰, 해안선이동, 부분반사 및 투과현상, 비선형 wave-wave interaction, 주파수분산, 방향분산 등 이다. 또한 이 모델은 파군이나 서프비트 현상을 모델링 할 수 있으므로 파랑변형에 의한 저주파수의 생성이나 소멸 등과 같이 세밀한 현상을 재현할 수 있고, 이러한 재현성은 항만공진, 부진동, 해안변형 등의 해석에 매우 중요하다(MIKE BY DHI, 2009a).
본 모델은 자유표면 수위 ξ와 수심 적분된 속도성분 P, Q에 대해서 평면 2차원으로 표시된 연속방정식과 운동량방정식의 확장 Boussinesq 방정식을 푼다.
연속방정식:
x 방향 운동량방정식:
y 방향 운동량방정식:
여기서 ψ1과 ψ2는 Boussinesq 분산 항으로서 다음과 같이 정의된다.
첨자 x, y, t는 각각 공간과 시간에 대한 미분 연산자를 의미한다. 그리고 Rxx, Ryy, Rxy는 쇄파현상 때문에 발생하는 불균등 속도분포에 기인한 초과운동량 항, Fx, Fy는 x, y 방향의 수평응력 항을 나타낸다. 또한 P, Q는 x, y 방향의 파속을 수심 적분한 flux density, B는 Boussinesq 분산계수, x, y는 데카르트 좌표, t는 시간, h는 수면변위까지의 수심(= d + ξ), d는 정수 면까지의 수심, ξ는 수면변위, g는 중력가속도, n은 공극률, C는 Chezy의 저항계수, β는 다공층 매체의 층류 흐름에 대한 저항계수, α는 다공층 매체의 난류 흐름에 대한 저항계수를 나타낸다.
수평방향 응력 항은 응력경사의 관계로부터 다음과 같이 정의 된다.
여기서 νt는 수평 와동점성계수이다.
그리고 쇄파현상 때문에 발생하는 불균등 속도분포에 기인한 초과운동량 항은 다음과 같이 정의된다.
여기서 δ = δ(t, x, y)는 정수면에서 쇄파 표면까지의 두께이고, cx, cy는 쇄파 파속의 x, y 방향 성분이다(MIKE BY DHI, 2009b). 자세한 내용은 Madsen et al.(1997)과 Sørensen et al.(2004)의 문헌에 기술되어 있다.
3.2 투과 파랑장 해석
본 연구에서는 투과제 주변의 부분투과파 및 부분반사파, 항내 안벽의 다중반사파 등을 포함한 복잡한 파랑장을 해석하여 항내에서 중력외파의 수면진동 현상을 해석한다. 여기서는 본 수치모델의 투과 파랑장 해석에 대한 타당성을 검증하고자 일본 토목학회 해안공학위원회의 연구보고서에서 제시된 투과파 검증계산 case와 본 모델의 결과를 비교하였으며(Coastal Engineering Committee, JSCE, 1993), 또한 투과파 검증계산 case를 이용하여 투과율 차이에 따른 중력외파의 투과 파랑장 변화를 검토하였다.
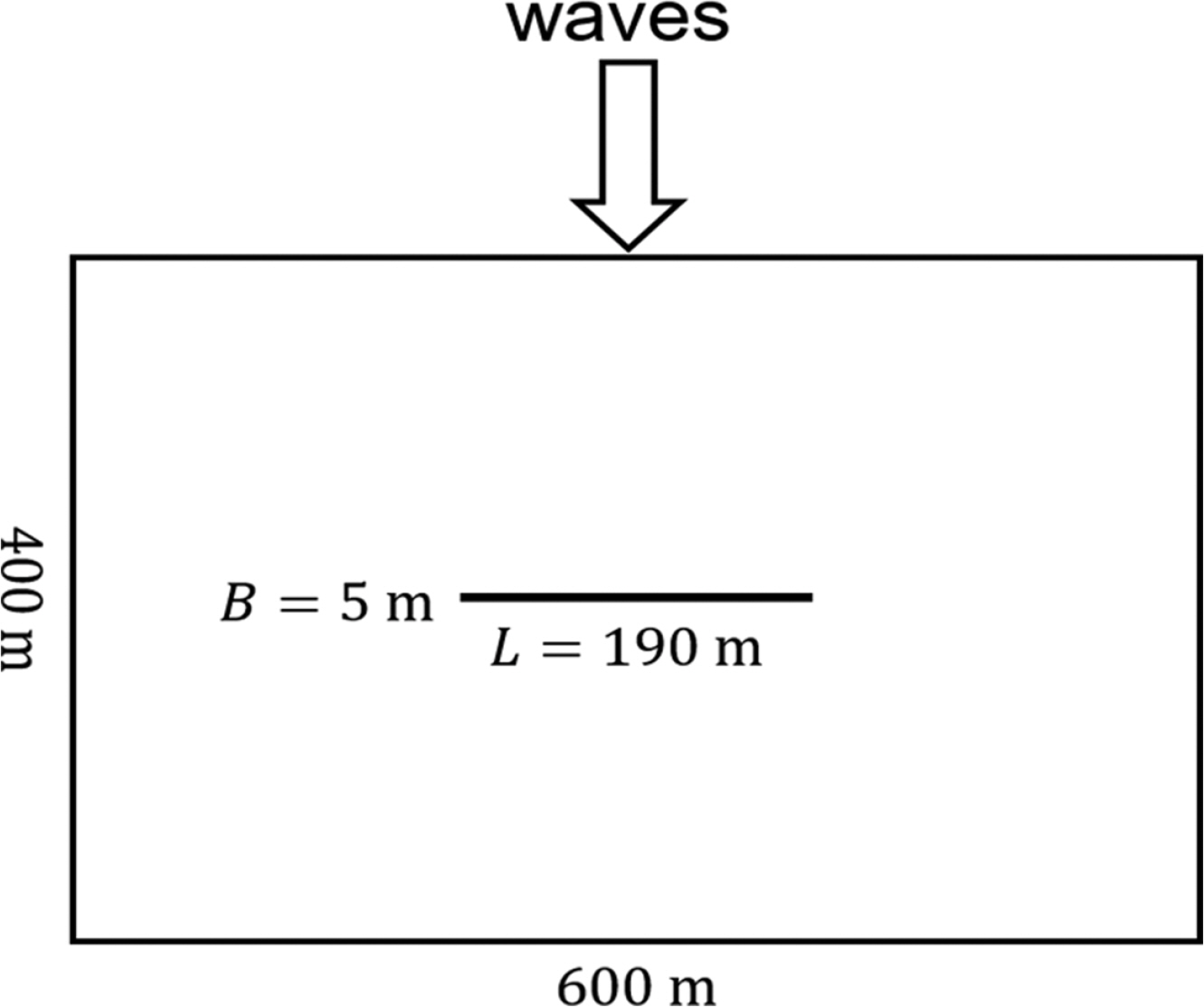
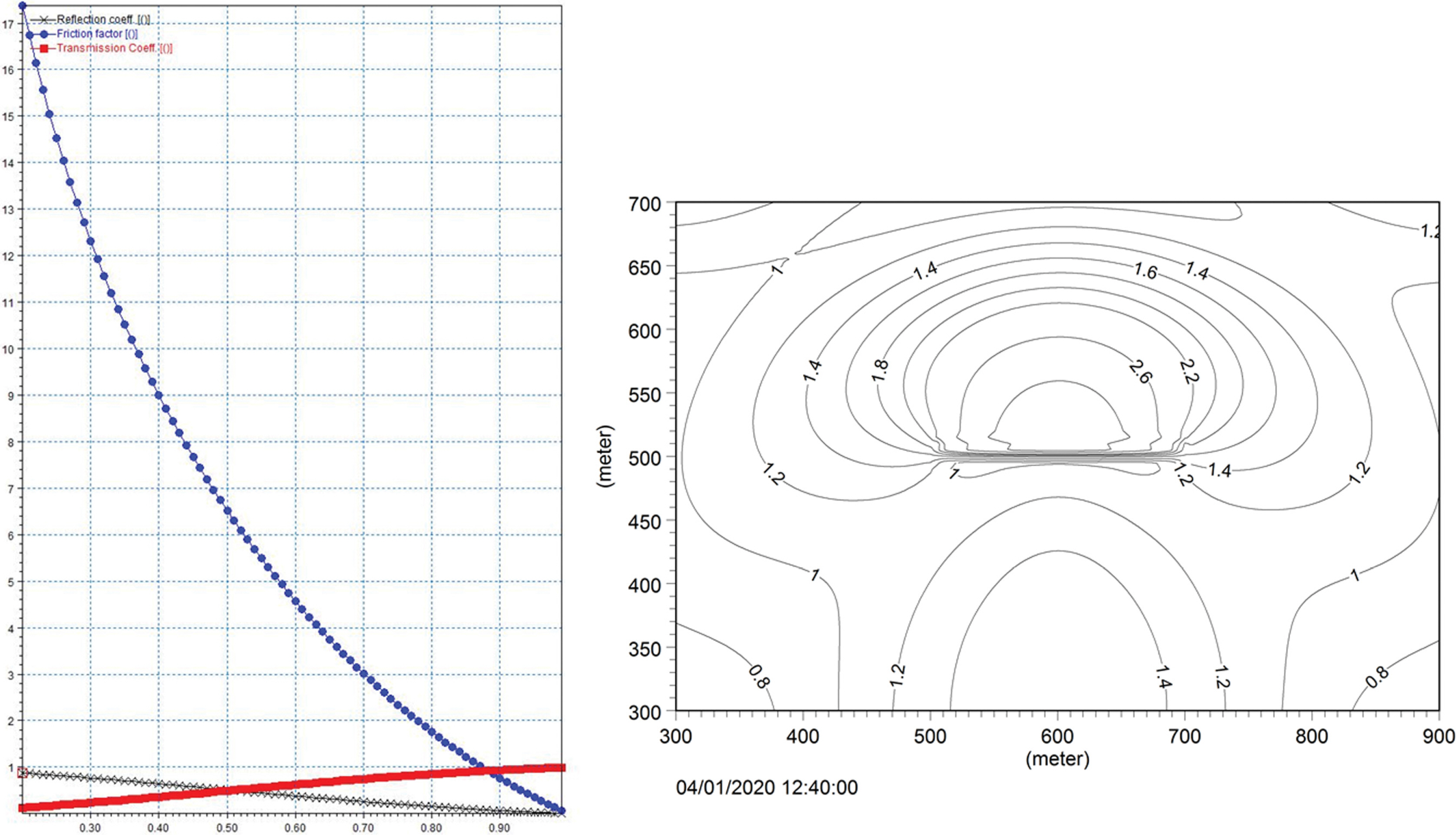
투과파 검증계산 case는 가로 600 m, 세로 400 m의 계산 영역 중앙에 길이 190 m, 제체 폭 5 m의 투과구조물이 설치된 경우이다(Fig. 3). 계산조건은 구조물의 투과율(Kt)은 0.3, 반사율(Kr)은 0.4이며, 수심은 10 m, 입사파의 파고와 주기는 각각 1.0 m와 5.0 s이다.
본 모델은 투과구조물의 위치에 공극계수(porosity coefficient)를 배치하여 부분투과파 또는 부분반사파를 재현한다. 공극계수는 구조물의 종류, 수심, 입사파의 주기 변수에 따라 달라지므로 투과율과 공극계수의 관계는 다양한 변수에 대한 반복 계산을 실시하고 관계 그래프를 구해서 사용한다. 투과율과 공극계수의 관계를 구하기 위한 입력 조건은 파고, 주기, 수심, 제체 폭은 검증계산의 조건과 동일하게 하였고 투과구조물의 종류는 사석제(rubble mound)로 하였다. 검증계산에 적용한 본 모델의 공극계수는 주기 5.0 s, 투과율 0.3일 때 0.48로 선정하였다.
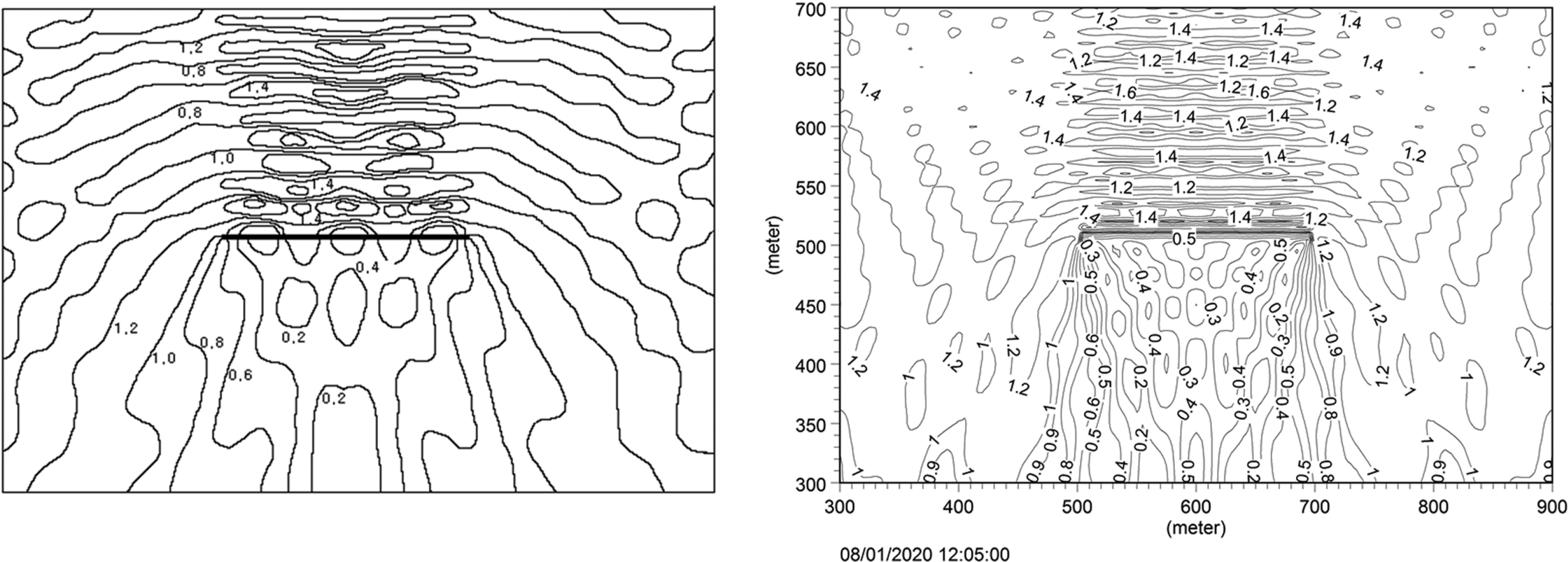
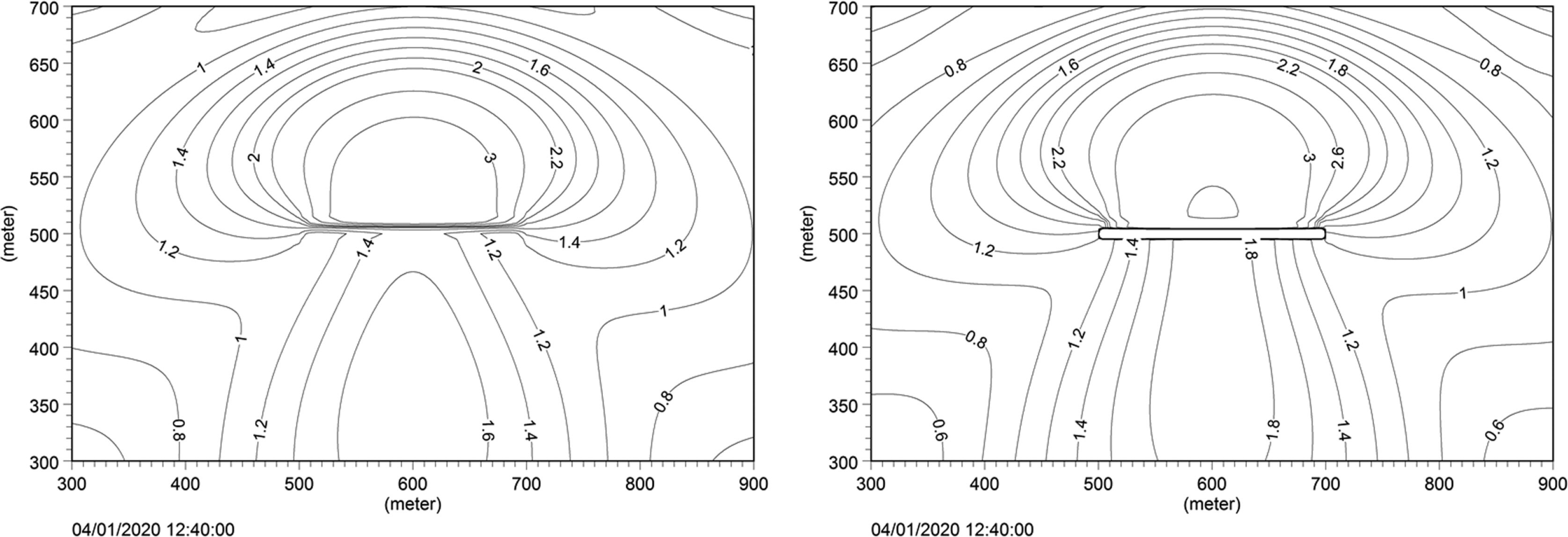
계산결과는 구조물 전면의 입·반사파의 공존 장에서는 부분중복파가 형성되어 1.0~1.4의 파고비분포를 보이고 있으며, 구조물 배후의 차폐영역에서는 부분투과파로 인하여 0.2~0.4의 파고비분포를 나타내었다. 두 결과는 구조물 전면 및 차폐영역에서 유사한 파고비분포를 나타내었다. 그러나 본 모델의 결과는 구조물 배후의 차폐영역을 벗어난 위치에서는 구조물 양단의 회절파가 전파되어 서로 중첩되고 있으며 0.5의 파고비분포를 나타내고 있다. 반면에 JSCE의 결과는 같은 위치에서 0.2의 파고비분포를 나타내고 있으며 이는 구조물에 의한 회절파가 충분히 재현되지 못한 것으로 생각된다(Fig. 4).
한편 중력외파에 대해서는 투과 파랑장의 검증 가능한 자료를 찾을 수 없어서 정량적인 검증은 못하였지만 투과파 검증계산영역을 이용하여 묵호항의 투과구조물 제원을 적용하고 투과율 차이에 따른 중력외파의 투과 파랑장 변화를 검토하였다. 묵호항 계산에 적용할 투과율과 공극계수의 관계는 주기 60.0 s, 파고 0.1 m, 수심은 10 m, 중앙입경이 0.2 m인 사석구조물의 조건으로 Fig. 5(left)와 같이 구하였다. 묵호항의 투과구조물은 투과율이 0.3과 0.13의 두 종류이고 공극계수는 관계그래프로부터 각각 0.35, 0.21로 선정하였다.
중력외파의 투과율이 0.3인 경우는 구조물 전면에서는 1.0~3.0의 파고비분포를 나타내었고 차폐영역에서는 1.2, 차폐영역을 벗어난 위치에서는 1.4의 파고비분포를 나타내었다(Fig. 5(right)). 구조물 전면에서는 파고비가 단주기파에 비해서 2배 정도 증가하고, 구조물 배후의 차폐영역을 벗어난 위치에서는 단주기파 보다 3배 정도 증가하였다. 중력외파의 경우 단주기 파보다 구조물 배후에서 파고가 크게 증가하는 이유는 구조물 전면에서 반사파가 크게 증가하고 이로 인하여 회절파의 에너지가 단주기파 보다 크기 때문으로 생각된다.
3.3 묵호항 수치계산조건
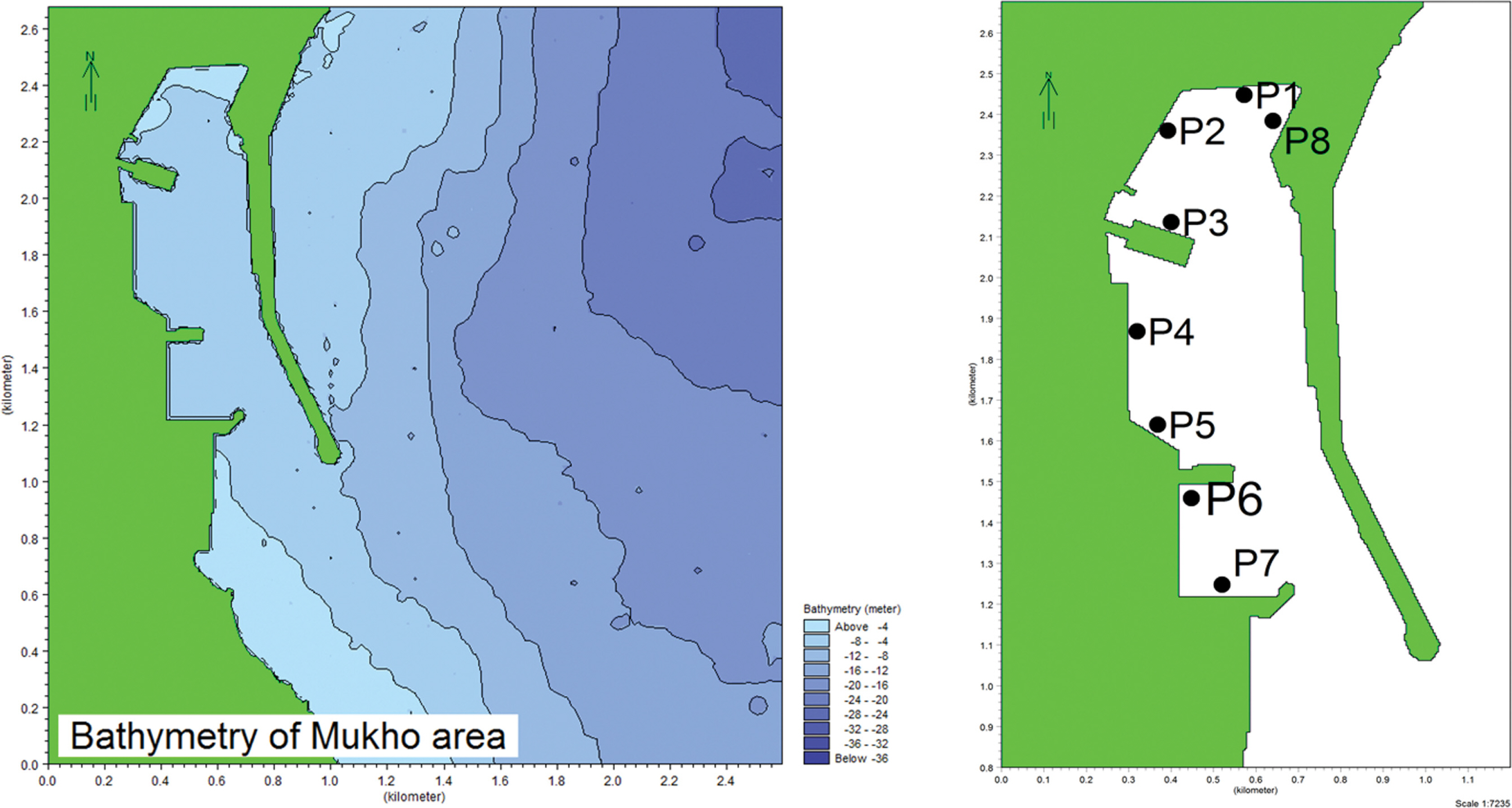
묵호항은 길이가 1,500 m이고 폭이 400 m인 좁고 긴 장방형의 기학적 형상을 갖고 있어서 장주기 파로 인한 항내 수면진동이 발달할 수 있는 조건이다. 수치계산은 항을 중심으로 남북방향으로 2,680 m, 동서방향으로 2,600 m의 영역을 설정하였고, 격자간격은 4.0 m로 하여 670 × 650개의 정방형 격자를 구성하였다. 계산영역의 수심은 외해 입사 역은 25 m, 항내는 4~8 m를 이루고 있으며, 중력외파의 반사율은 항내 안벽 0.99, 소파블록 0.98, 자연해안 0.97로 설정하였다(Fig. 7 (left)).
입사파 조건은 파랑관측 자료에서 추출된 중력외파를 사용하였다. 주기는 30 s~125 s 범위에서 64 cases로 분할하였고, 파고는 파랑 출현율을 고려하여 0.1 m로 설정하였다. 이 때 파향은 주변 강릉해역에서 관측된 파향별 출현율을 참조하여 N~SE 방향을 22.5°의 간격으로 분할하여 7개 파향을 고려하였다.
MIKE21의 Boussinesq Wave Model은 시간영역을 해석하는 비정상모델이므로 격자간격, 시간간격, 파속에 따라 Courant number가 달라지는데 본 연구에서는 입사파의 주기에 따라 계간시간간격을 dt = 0.25 s, 0.40 s로 적용하여 Cr ≤ 0.9, 1.4인 조건으로 계산하였다. 그리고 각 case의 총 계산시간은 항내에서 정상파가 충분히 발달할 수 있도록 입사파의 20주기로 하였다.
3.4 항내 수면진동 해석 결과
장주기 파가 장방형 형상의 항만으로 입사되면 반사파의 에너지가 항 외로 산란되지 못하고 정상파 운동을 하는 수면진동이 발생하게 된다. 묵호항은 외해로부터 직접 입사하는 파랑의 작용을 받는 지형적인 특성과 좁고 긴 기하학적 형상 때문에 중력외파와 같은 장주기파의 전파에 의한 항내 수면진동현상이 큰 수역이다.
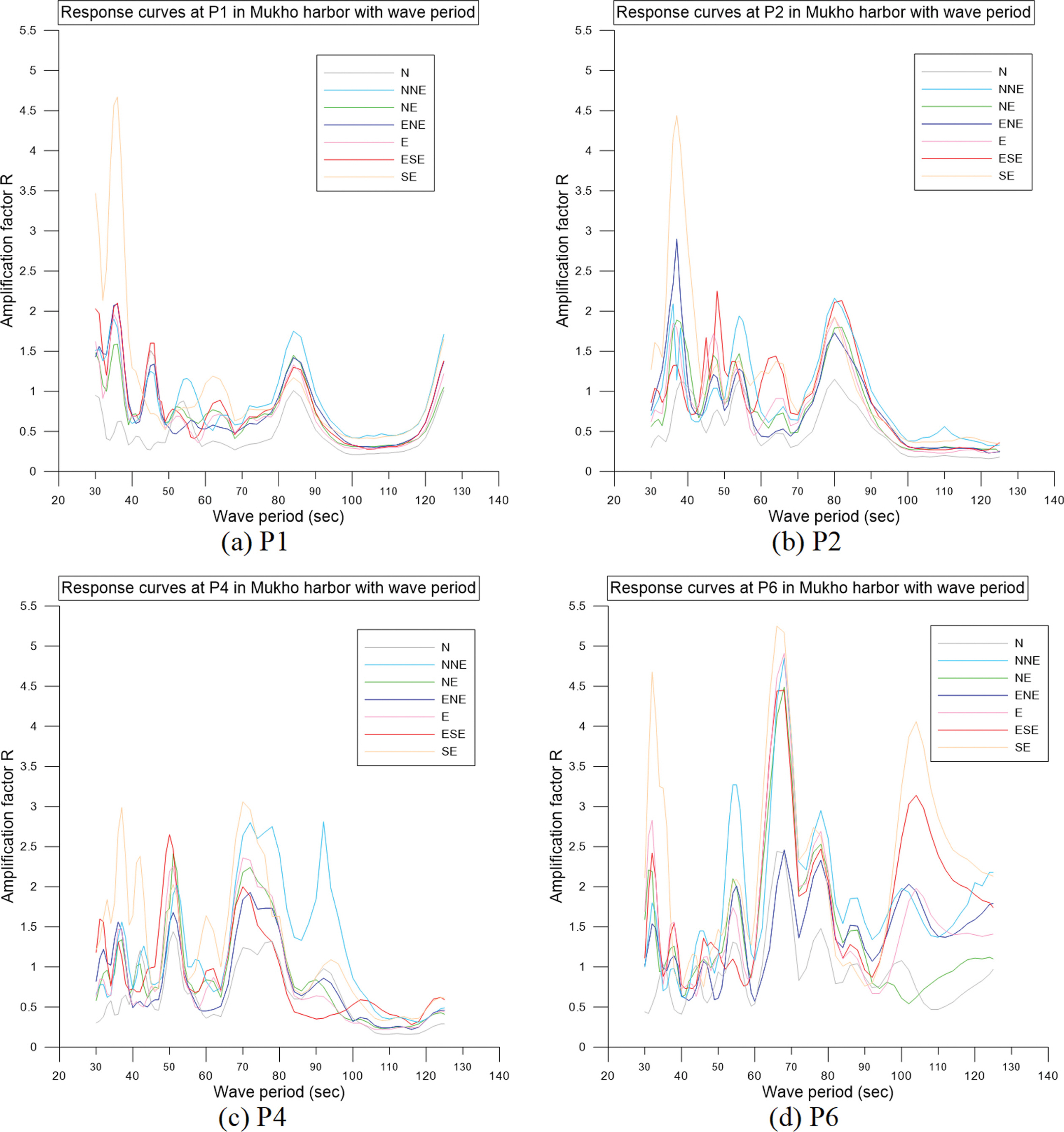
본 연구에서는 묵호항의 수면진동 저감 목표 주기를 찾기 위해서 저감 방법을 적용하기 전의 항내 수면진동 현상을 해석하였다. 항내 수면진동 해석 결과는 항내에 8개의 측정 점을 설정하고(Fig. 7(right)), 각 측정 점에 대한 진폭응답곡선을 구하여 중력외파의 주기 및 파향에 따른 항내 수면진동 변화를 파악하였다. 항내 P1, P2, P4, P6점에서 주기에 따른 진폭응답곡선을 나타내면 Fig. 8과 같다. 여기서 수평 축은 입사파 주기, 연직 축은 항내 측정 점의 파고를 입사파고로 나누어 무차원화 시킨 진폭계수를 나타낸다.
Fig. 8(a)는 항 내측에 위치한 P1점의 진폭응답곡선으로서 주기 36.0 s일 때 입사파의 진폭은 항내에서 4.7배로 증가하였다. Fig. 8(b)는 P2점의 응답곡선으로서 38.0 s일 때 피크를 나타냈으며 이 때 진폭계수는 4.5이었다. Fig. 8(c)는 항 중간에 위치한 P4점의 응답곡선으로서 37.0 s, 50.0 s, 70.0 s, 92.0 s에서 피크를 나타내며 이때의 진폭계수는 각각 3.0, 2.7, 3.1, 2.8로 산정되었다. 그리고 Fig. 8(d)는 항 입구와 가까운 P6점의 응답곡선으로서 32.0 s, 55.0 s, 68.0 s, 78.0 s, 110.0 s에서 공진모드 나타나며 이때의 최대 진폭계수는 각각 4.7, 3.3, 5.3, 3.0, 4.1로 산정되었다. 주방파제 선단에서 회절된 파랑과 항 남측의 호안에서 반사된 파랑이 항내로 전파하여 항입구에 위치한 정방형 형상의 P6 수역에서 공진현상이 발생하고 수면진동이 크게 발달하였기 때문으로 판단된다.
본 연구에서는 중력외파에 의한 수면진동이 가장 크게 나타난 P6점의 주기 68.0 s를 저감 목표 주기로 결정하였고, 이때 주 파향은 강릉의 방향별 파랑 출현율을 참고하여 NE 방향으로 선정하였다.
4. 수면진동 저감 효과분석
4.1 저감 방법
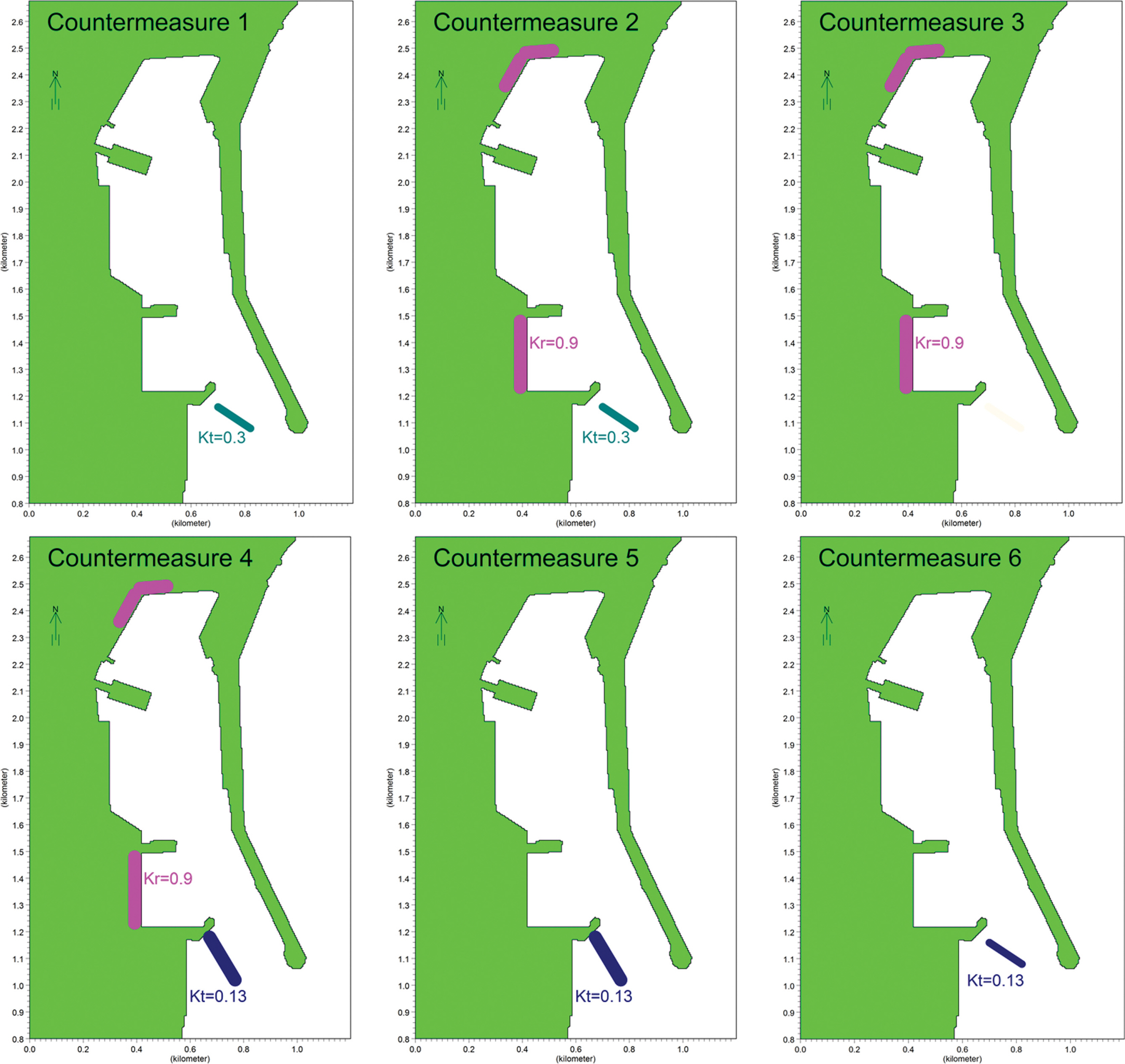
중력외파에 의한 항내 수면진동의 저감 방법은 항 외측에 투과제를 추가하여 중력외파의 에너지를 차단하고 목표 주기를 이동시키는 기하학적 변화 방법과 항내 안벽의 일부 구역을 저반사 구조형식으로 교체하여 중력외파의 에너지를 감소시키는 방법을 적용하였다. 저감 방법은 길이 120 m, 투과율 0.3의 투과제를 항 외측에 도제 형태로 설치하는 방법(저감 방법 1, 2), 길이 200 m, 투과율 0.13의 투과제를 주방파제와 평행하게 설치하는 방법(저감 방법 4, 5), 항내의 직립 안벽을 에너지흡수 구조형식으로 교체하는 방법(저감 방법 2, 3, 4), 그리고 저감 방법 6은 저감 방법 1에서 투과율을 0.13으로 변경한 경우로서 모두 6가지 방법을 설정하였다(Fig. 9).
4.2 저감 효과 비교
(1) 진폭응답곡선 비교
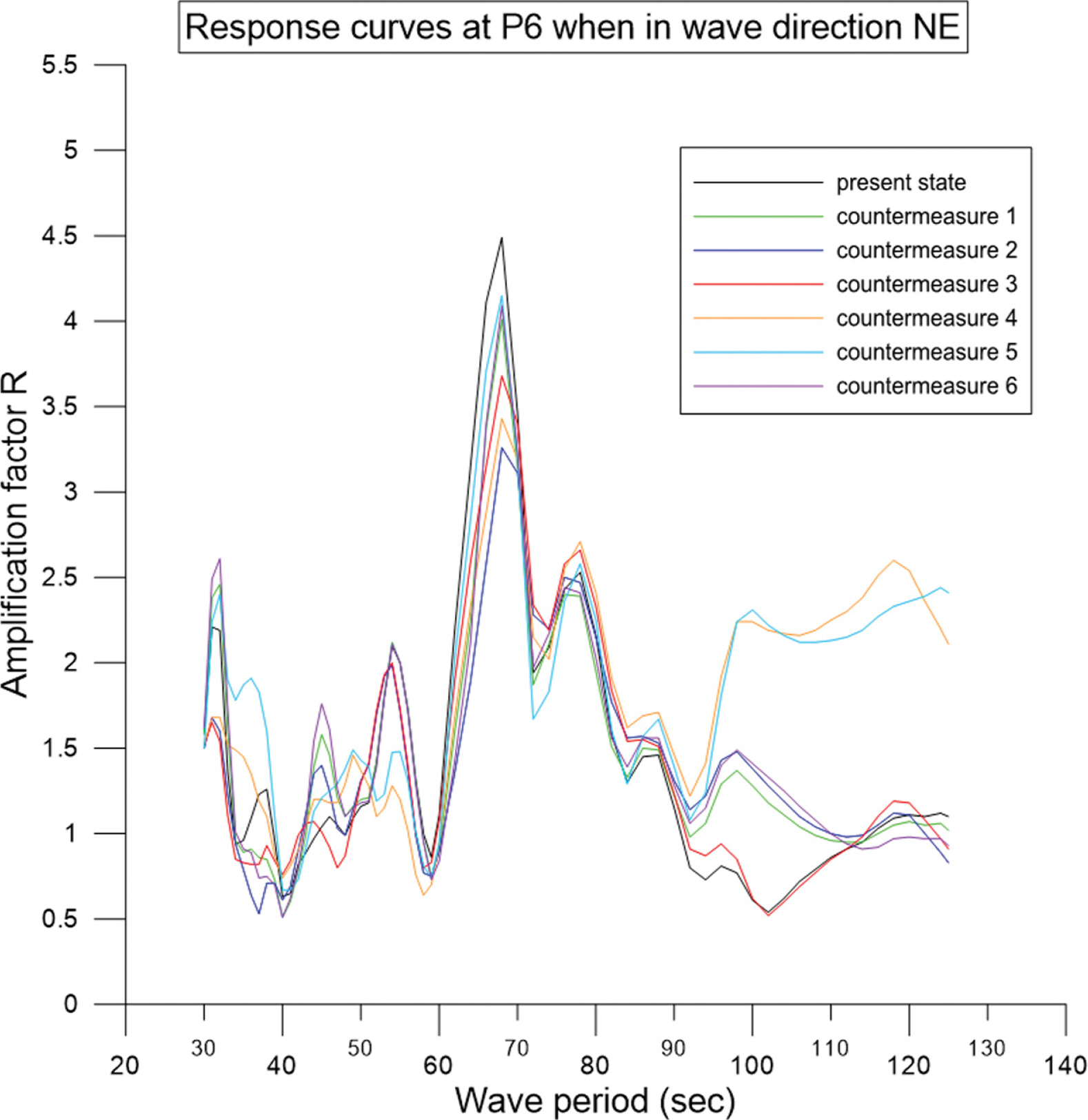
항내 수면진동 저감 효과는 항내 측정 점 8곳에서 저감 방법 적용 전·후의 진폭응답곡선을 비교하여 검토하였다. Fig. 10은 파랑 출현율이 가장 높은 NE 방향으로부터 중력외파가 입사할 때 항내 측정 점들 중에서 수면진동이 가장 큰 P6점의 진폭응답곡선을 비교한 것이다. 그림에서 검정색 선은 저감 방법 적용 전의 결과이고 칼라로 표시한 선들은 저감 방법 적용 후의 결과들이다.
저감 방법 적용 전·후의 진폭응답곡선을 비교하면 첨두 주기 55.0 s, 78.0 s, 110.0 s에서는 진폭계수가 모두 2.5 이하이고 저감 방법 적용에 따른 진폭 감소가 크지 않으나 32.0 s, 68 s일 때는 저감 방법 적용에 따른 진폭감소가 뚜렷이 나타났다. 특히 파랑색으로 표시된 저감 방법 2는 첨두 주기 68 s에서 진폭이 다른 방법보다 가장 크게 감소하였다.
(2) 투과율 및 기하학적 형상 변화에 따른 저감 효과 비교
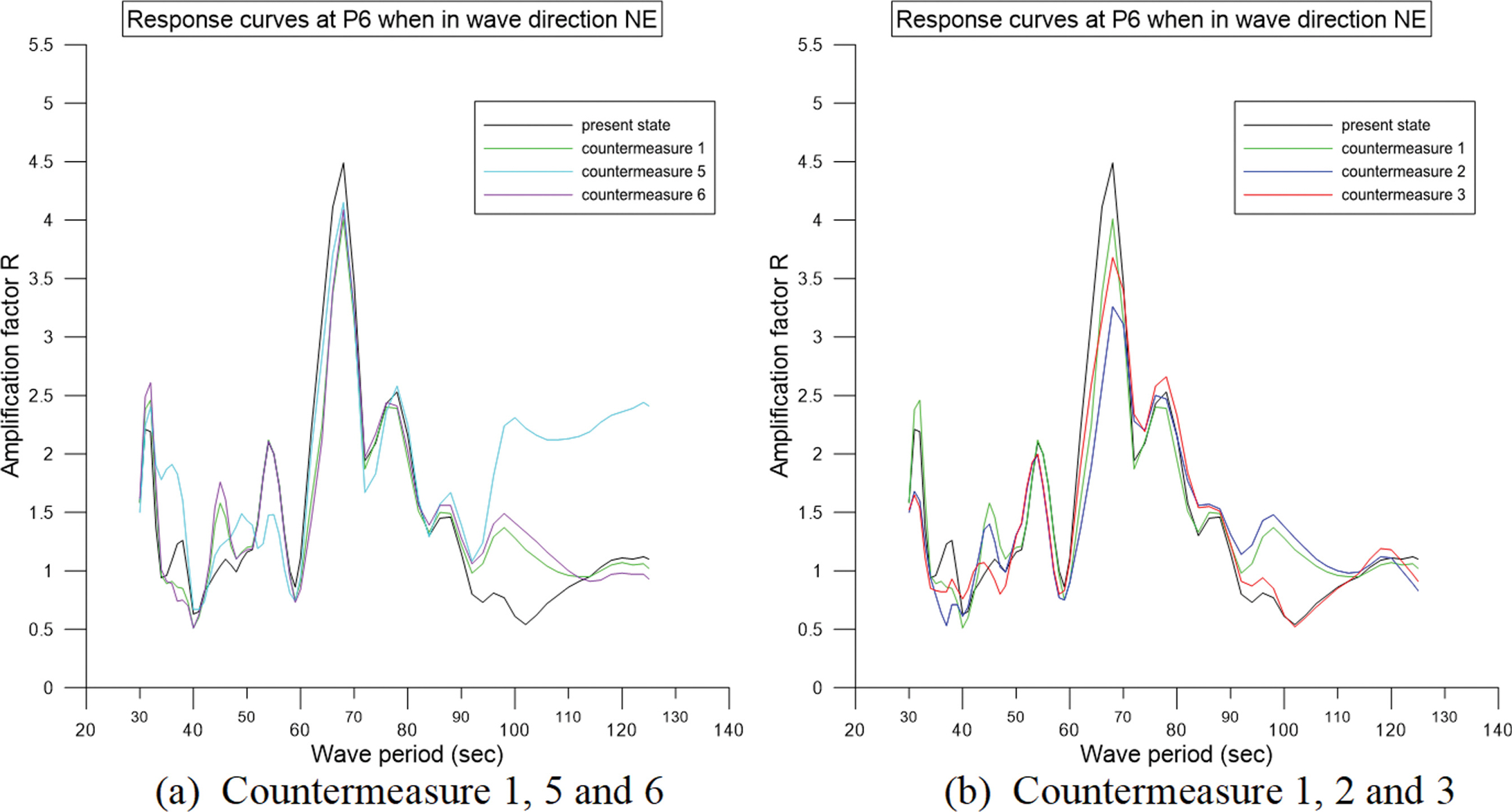
저감 방법 1과 6은 투과구조물의 길이와 위치가 동일한 기하학적 형상을 갖고 있지만 투과율이 0.3과 0.13으로 서로 다르다. 두 방법의 저감 효과는 항 내 측정 점 P6에서 진폭응답 곡선이 매우 유사하여 큰 차이가 없음을 알 수 있다. 진폭계수는 주기 68.0 s일 때 저감 방법 적용 전의 4.49에서 저감 방법 1과 6을 적용하면 각각 4.00과 4.09로 감소하였고 투과율 차이에 따른 수면진동 저감 효과는 유사한 것으로 나타났다(Fig. 11(a)). 이것은 중력외파와 같은 장주기 파는 구조물의 투과율이 커짐에 따라 투과파는 증가하지만 반사파가 상대적으로 작아져서 회절파의 영향이 줄어드는 반면에 투과율이 작은 경우는 투과파는 줄어들지만 반사파가 더욱 증가하여 파랑에너지가 매우 높아지고 이로 인하여 회절파가 차폐영역 안쪽까지 전파하면서 구조물 배후에서는 투과율이 조금 차이나도 파고분포에는 큰 차이가 없기 때문으로 판단된다.
저감 방법 5와 6은 구조물의 투과율이 0.13으로 동일하지만 구조물의 길이 및 방향 등 기하학적 형상이 서로 다른 경우이다. 두 방법은 첨두 주기 32.0 s, 55.0 s, 68.0 s, 78.0 s에서는 진폭응답곡선이 유사하며 저감 효과는 차이가 없지만 저감 방법 5의 경우는 주기 90 s~120 s에서 진폭이 크게 증가하는 것을 알 수 있다(Fig. 11(a)). 이러한 현상은 투과제를 주방파제와 평행하게 연장함으로서 항의 특성길이가 저감 방법 적용 전보다 증가되었기 때문으로 생각한다.
(3) 기하학적 변화 방법과 에너지흡수 방법의 저감 효과 비교
기하학적 변화 방법은 방법 1, 5, 6이고 에너지흡수 방법은 방법 3이다. 저감 효과는 첨두 주기가 32.0 s와 68.0 s일 때 에너지흡수 방법이 기하학적 변화 방법보다 더욱 좋은 것을 알 수 있다. 항내 안벽을 유공 또는 사석구조물로 처리하여 중력외파의 에너지를 흡수하는 방법은 진폭계가 큰 첨두 주기에서 수면진동 저감 효과가 더욱 큰 것을 확인하였다. 한 편 두 방법을 조합한 저감 방법 2는 첨두 주기 68.0 s에서 에너지흡수 방법만 적용할 때보다도 더욱 높은 저감 효과를 나타내었다(Fig. 11(b)).
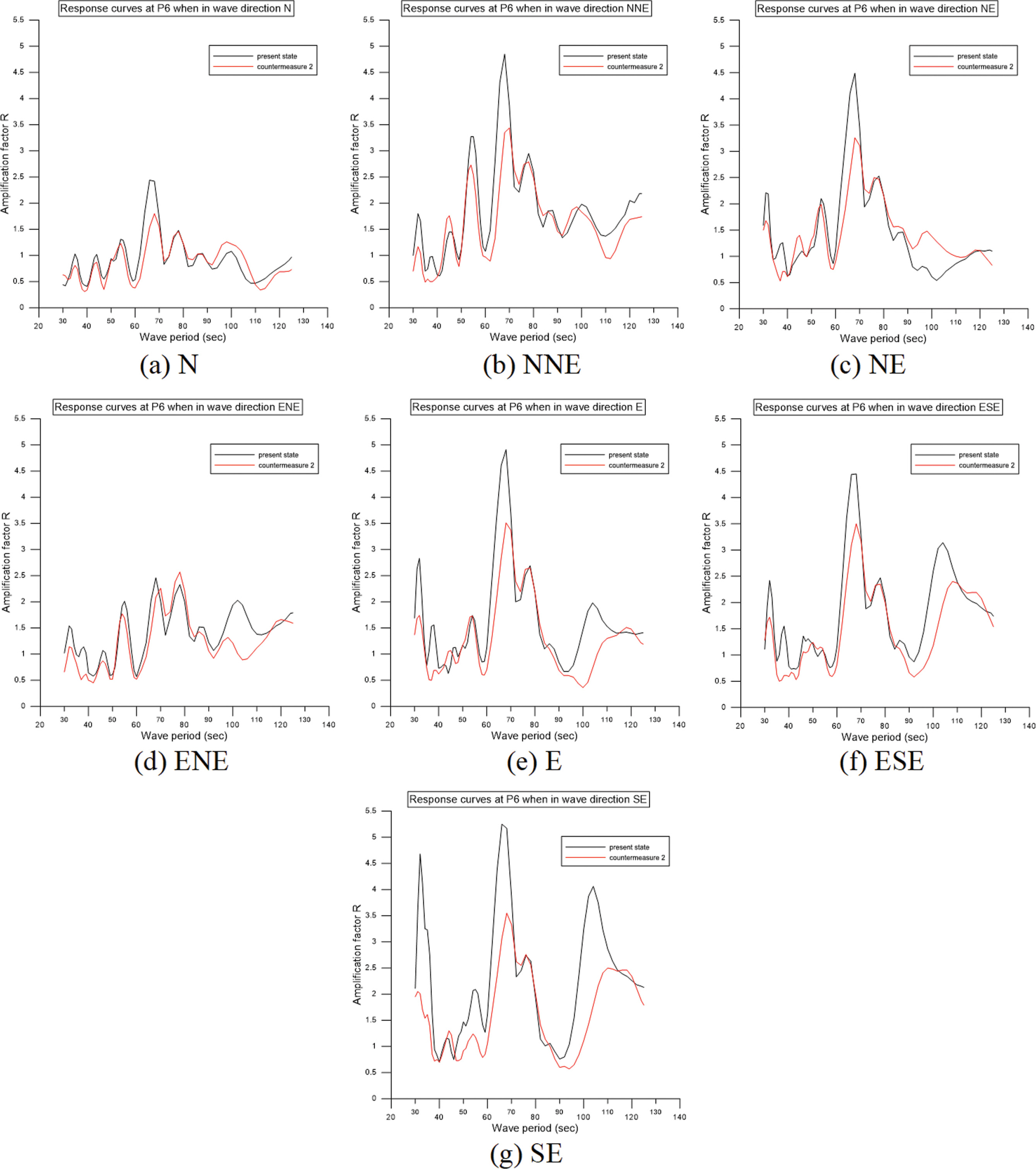
(4) 파향별 저감 효과 비교
파향에 따른 저감 효과는 항내 수면진동 저감 효과가 가장 좋았던 방법 2에 대해서 검토하였다. 저감 방법 2는 모든 파향에 대해서 수면진동 저감 효과가 뚜렷이 나타났으며, 여러개의 첨두 주기가 나타나는 NNE, NE, E, ESE, SE 방향에 대해서는 저감 방법 적용 전의 진폭을 크게 감소시켰다. 특히 각 파향에서 진폭계수가 가장 큰 첨두 주기 68.0 s에서는 진폭의 감소가 더욱 크게 나타났으며, SE 방향은 첨두 주기 32.0 s, 68.0 s, 110.0 s 등 모든 첨두 주기에서 진폭을 크게 감소시키는 것을 알 수 있었다(Fig. 12).
(5) 진폭 감소율 비교
본 연구에서는 각 수면진동 저감 방법의 효과를 정량적으로 검토하기 위하여 저감 방법 적용에 따른 진폭 감소율을 비교하였다. 여기서는 P6점에 대해서 파랑 출현율이 가장 높은 NE 방향에서 중력외파가 입사할 때 첨두 주기 68.0 s에서의 진폭 감소율을 구하였다(Table 2).
진폭 감소율은 항 외측에 투과율 0.3의 투과제를 설치하고 항내의 일부를 에너지흡수 구조형식으로 교체하는 저감 방법 2가 27.4%로 가장 높았으며, 그 다음은 항 외측에 투과율 0.13의 투과제를 주방파제와 평행하게 설치하고 항내의 일부 구역을 에너지흡수 구조형식으로 교체하는 저감 방법 4가 23.6%를 나타내었다. 그리고 항내에 에너지흡수 구조형식을 도입하는 저감 방법 3은 감소율이 18.0%로 얻어졌으며, 항외측에 투과제만 설치하는 저감 방법 1은 10.9%, 저감 방법 5는 7.6%, 저감 방법 6은 8.9%를 나타내었다.
중력외파와 같은 장주기파는 항내에 파랑에너지흡수 구조형식의 구조물을 설치하는 방법이 효과적인 저감 방법임을 알 수 있으며 항 외측에 투과제를 같이 설치하면 수면진동 저감효과가 더욱 증가함을 알 수 있다.
5. 결 론
본 연구에서는 투과구조물과 에너지흡수 구조형식을 이용한 중력외파의 항내 수면진동 저감 방법을 묵호항에 적용하고 Boussinesq 파랑모델을 사용하여 저감 효과를 수치적으로 검토하였다. 본 연구를 통하여 얻은 결론은 다음과 같다.
(1) 묵호항의 중력외파는 5년간의 장기 연속파랑관측자료를 분석한 결과 주기는 40 s~70 s 사이에 집중 분포하였고, 파고는 0.1 m 이하가 분석 대상 자료의 94%이었다.
(2) 중력외파가 묵호항내로 전파할 때 항 입구 수역의 P6점에서 수면진동현상이 가장 크게 발생하였고 첨두 주기는 32.0 s, 55.0 s, 68.0 s, 78.0 s, 110.0 s이었다. 이 때 가장 큰 진폭계수는 주기 68.0 s일 때 5.3이었다.
(3) 가장 효과적인 수면진동 저감 방법은 항 외측에 투과율 0.3의 투과방파제를 도제로 설치하고, 항내 안벽의 일부 구역을 파랑에너지흡수 구조형식으로 교체하여 중력외파에 의한 반사율을 0.9 이하로 낮추는 방법이었으며 이 방법의 진폭 감소율은 P6점에서 NE 방향, 주기 68.0 s일 때 27.4%이었다.
(4) 투과방파제의 투과율 변화가 중력외파의 항내 수면진동 저감 효과에 미치는 영향은 크지 않았다. 이것은 중력외파와 같은 장주기파의 경우 구조물에 의한 회절현상이 매우 크게 발생하기 때문이다. 투과율이 크면 투과파가 증가하면서 상대적으로 반사파가 감소하여 회절파의 파고가 작아지고, 반면에 투과율이 작으면 투과파는 감소하지만 반사파가 증가하여 회절파의 파고가 높아지기 때문에 투과제 배후의 차폐 영역에서는 투과율 차이에 따른 파고분포 변화가 크지 않다. 이러한 현상은 중력외파에 대한 투과 파랑장의 검증계산으로 부터 확인할 수 있었다.
(5) 항내의 일부 구역을 파랑에너지흡수 구조형식으로 교체하는 방법은 중력외파의 수면진동 저감 효과가 좋으나 주기 60 s~70 s 정도의 장주기 파의 에너지를 감소시키기 위해서는 구조물의 폭이 크게 증가하기 때문에 반사율을 0.9 이하로 제어할 수 있으면서 구조물의 폭이 좁은 구조형식이 필요하다.