요약연안에서 천수변형에 의해 발생하는 쇄파는 표사이동, 연안류의 생성, 충격파압의 발생 등과 같은 연안역의 다양한 물리현상과 밀접한 관계를 갖고 있다. 따라서, 연안구조물의 설계 시 쇄파파고 및 쇄파수심과 같은 쇄파지표를 정확하게 예측하는 것이 중요하다. 과거부터 많은 연구자들에 의해 쇄파현상을 규명하고 예측하기 위한 많은 과학적인 노력들이 이루어져 왔다. 대표적인 쇄파에 연구들은 주로 수리모형실험을 통해 쇄파지표 예측을 위한 많은 경험식이 제안되어 왔다. 하지만, 기존의 쇄파지표에 대한 경험식은 일정한 방정식의 가정하에 자료의 통계적 분석을 통해 가정한 방정식의 계수들을 결정하고 있다. 본 논문에서는 회귀 혹은 분류문제와 관련된 다양한 연구분야에 있어서 높은 예측성능을 보여주는 대표적인 선형기반의 지도학습 머신러닝 기법을 적용하였다. 적용된 머신러닝 기법을 기반으로 기존의 쇄파에 대한 실험자료로부터 쇄파지표 예측을 위한 모델을 개발하고, 학습된 모델로부터 쇄파 예측을 위한 새로운 선형식을 제시하였다. 새롭게 제안된 쇄파지표식은 단순한 선형식임에도 불구하고 기존의 경험 공식에 비해 유사한 예측성능을 보였다.
AbstractBreaking waves generated by wave shoaling in coastal areas have a close relationship with various physical phenomena in coastal regions, such as sediment transport, longshore currents, and shock wave pressure. Therefore, it is crucial to accurately predict breaker index such as breaking wave height and breaking depth, when designing coastal structures. Numerous scientific efforts have been made in the past by many researchers to identify and predict the breaking phenomenon. Representative studies on wave breaking provide many empirical formulas for the prediction of breaking index, mainly through hydraulic model experiments. However, the existing empirical formulas for breaking index determine the coefficients of the assumed equation through statistical analysis of data under the assumption of a specific equation. In this paper, we applied a representative linear-based supervised machine learning algorithms that show high predictive performance in various research fields related to regression or classification problems. Based on the used machine learning methods, a model for prediction of the breaking index is developed from previously published experimental data on the breaking wave, and a new linear equation for prediction of breaker index is presented from the trained model. The newly proposed breaker index formula showed similar predictive performance compared to the existing empirical formula, although it was a simple linear equation.
1. 서 론심해에서 연안으로 전파되는 파랑은 수심의 영향에 의해 파속이 감소되며, 이는 파장의 감소와 더불어 결과적으로 파고의 증가를 발생시킨다. 특히, 주기가 긴 파랑일수록 해저바닥과의 상호작용이 빠르게 발생한다. 연안에서 증가된 파고가 일정한 한계 파형경사에 도달하게 되면 쇄파가 시작된다. 이러한 쇄파는 연안에서 발생하는 연안류, 표사이동, 충격파압, 에너지소산 등 다양한 물리현상과 직접적인 관계가 있으므로 쇄파현상을 규명하기 위해 Stokes(1880)에 의한 쇄파 연구 이후로 과거 140년간 쇄파에 관한 연구가 지속되어 왔을 만큼 해안공학에 있어서 매우 중요한 난제 중의 하나이다. 계측기기의 발달과 더불어 1950년대 이후부터 쇄파에 대한 수리모형실험이 본격적으로 수행되었으며, 실험결과를 바탕으로 쇄파의 정량적인 평가를 위한 다양한 경험식이 제안되고 있다. 최근에는 계산기 성능의 비약적으로 향상됨에 따라 전산유체 역학(Computational fluid dydnamics, CFD)을 기반으로 쇄파에 대한 발생기구에 대하여 직접적인 수치해석을 시도하는 연구가 급속하게 증가하고 있다(Lin and Liu, 1998; Bradford, 2000; Zhao et al., 2004; Hieu et al., 2004; Christensen, 2006; Lee et al., 2007; Chella et al., 2015). CFD를 이용한 수치 시뮬레이션은 쇄파에 밀접하게 관계된 점성의 영향, 난류의 생성, 기체의 운동 및 수면경계에서의 밀도변화 등을 고려할 수 있는 장점이 있다. 하지만 여전히 CFD기반의 수 치모델은 많은 계산비용이 소요된다는 점을 지적하지 않을 수 없다. 따라서, 쇄파에 대한 실험결과에 의존하여 보다 높은 예측정도를 갖는 쇄파지표 산정식을 제안하는 연구가 지속되고 있다.
최근에 Liu et al.(2011)은 기존에 제안된 쇄파지표에 관한 경험식을 McCowan, Miche, Goda 및 Munk-type(McCowan, 1984; Miche, 1944; Goda, 2010; Munk, 1949)의 4개로 분류하여 각각의 경험식을 기존의 실험데이터와 비교·분석하였다. 그 결과, 심해파형경사를 파라메터로 하는 Goda 형식의 경험식이 비교적 높은 예측성능을 보이지만 사면경사에 따른 오차가 존재함을 확인하였다. 이에 Liu et al.(2011)은 사면경사에 독립된 쇄파지표 산정을 위해 천해조건에서 선형이론의 파속을 이용한 경험식을 제안하였다. Rattanapitikon and Shibayama(2006)는 쇄파파고와 쇄파수심에 대한 양해적 산정이 가능한 경험식을 제안하였으며, Goda(2010)는 기존에 Goda 경험식(Goda, 1970)이 갖는 급경사면에서의 낮은 쇄파 예측성능을 보완하기 위해 기존의 경험식을 수정하여 제안하였다. 또한, Xie et al.(2019)는 정도 높은 쇄파수심 예측을 위해 천수방정식으로부터 해석해를 유도하고 기존의 실험데이터를 적용하여 검증한 반경험 공식을 제안하고 있다.
한편, 사용자가 명시적으로 프로그래밍을 하지 않고도 컴퓨터가 입출력 자료로부터 통계적 구조를 검색하여 자동으로 일정한 규칙을 생산할 수 있는 인공지능(artificial intelligence, 이하 AI)의 한 분야인 머신러닝(machine learning, 이하 ML) 알고리즘이 다양한 분야에서 활발하게 활용되고 있다. 실제 머신러닝에 대한 최초의 시도는 60년 전에 체스게임 방법을 컴퓨터 학습시키기 위한 Samuel(1959)의 연구로부터 시작되었지만, 최근 들어 데이터 저장비용 감소에 따른 빅데이터의 등장, 다양한 ML 알고리즘 개발 및 컴퓨팅 기술의 발달과 더불어 ML을 활용한 연구가 여러 분야에서 활발하게 활용되고 있다.
해안공학분야에 있어서도 ML을 이용한 연구 예가 꾸준하게 증가하고 있다. Kim and Park(2005)은 ML 알고리즘 기반의 사석방파제의 설계 및 신뢰성 분석 모델을 제안하였으며, Kazeminezhad and Etemad-Shahidi(2015)와 Etemad-Shahidi et al.(2016)은 연직파일의 처오름 높이와 연직구조물에 대한 월파량 산정을 위해 ML 알고리즘을 적용하였으며, Formentin and Zanuttigh(2019)는 월파량에 미치는 천단높이의 감소효과를 예측하기 위해 ML 알고리즘에 기반한 새로운 공식을 제안하였다. James et al.(2018)은 연안에서 파랑 추산을 위해 ML 기반 모델을 구축하고 기존의 SWAN 모델에 비해 비약적인 계산비용이 감소함을 보였고, Stringari et al.(2019)과 Buscombe et al.(2020)은 ML 알고리즘을 이용하여 쇄파대에서 효과적인 파랑 추적이 가능함을 증명하였다. 국내에서도 ML 알고리즘을 활용한 연구가 증가하고 있지만 주로 인공신경망(artificial neural network, 이하 ANN)에 제한된 연구가 대부분이다(Kim et al., 2010; Kim and Suh, 2011; Oh and Jeong, 2015; Lee and Suh, 2016; Yi et al., 2017; Lee et al., 2020). ANN은 생물계의 신경망과 유사하게 공학적으로 모델화한 학습 알고리즘으로 비선형성의 취급이 가능하다는 특징으로 인해 다양한 분야에서 광범위하게 이용되는 ML 모델이다. 하지만, ANN의 예측성능은 학습을 위한 훈련 데이터의 질과 크기에 크게 의존하며, 최적의 네트워크를 구축하기 위해서는 시행착오를 통한 개발자의 경험이 요구된다는 점이 지적되고 있다(Ren, 2012; Bataineh and Marler, 2017).
쇄파와 관련한 문제에 대하여 Lee et al.(2020)은 다층 ANN을 적용한 딥러닝(deep learning)을 통해 기존에 제안된 쇄파지표의 경험식에 비해 ANN이 보다 높은 예측성능을 보임을 증명하였다. 하지만, ANN은 앞서 기술한 바와 같이 여전히 학습과정에서 최적의 파라메터를 찾기가 어렵고, 입력 변수와 출력변수 사이의 설명기능이 부족하다. 이러한 ANN의 단점은 많은 엔지니어들이 ANN 모델을 쉽게 수용하지 못하는 원인을 제공할 수 있다. 또한, 기존에 제안된 쇄파예측 경험식의 대부분은 지수함수 혹은 쌍곡선 함수를 기저로 하고 있어 손쉬운 계산이 곤란하다.
본 연구에서는 쇄파와 관련된 입력변수와 출력변수 사이의 관계가 설명 가능한 선형회귀모델을 기반으로 지도학습 ML 알고리즘을 이용하여 쇄파예측을 위한 새로운 선형식을 제안한다. ML을 위한 학습 데이터와 평가 데이터는 일정 경사면에서 수행된 기존의 쇄파 연구로부터 획득한 수리모형실험 데이터를 이용하였다. ML의 알고리즘은 기본적인 선형모델(linear model, LM)과 회귀문제와 관계된 연구에서 양호한 예측성능으로 자주 활용되는 서포트 벡터 머신(support vector machine, SVM)을 적용하였다. 선택한 ML 기법을 이용하여 천수변형에 의해 경사면에서 발생하는 쇄파지표 예측모델을 구축하고 기존에 제안된 경험식과의 비교·분석을 통해 그 적용 가능성을 제시한다. 또한, ML 예측모델을 통해 손쉬운 계산이 가능한 쇄파지표에 대한 새로운 산정식을 제안한다.
2. 쇄파관련 실험자료2.1 쇄파에 대한 물리량 정의앞서 기술한 바와 같이 지금까지 쇄파에 관한 수리모형실험은 여러 연구자들에 의해 꾸준히 수행되어 왔으며, 적지않은 실험자료가 축적되었다. 하지만, 쇄파시점의 정의에는 실험별로 완벽하게 일치하지 않는다. 즉, 파고가 최대로 도달한 시점을 쇄파로 정의하는 경우와 파랑의 전면이 수직이 되는 시점을 쇄파로 정의하는 경우, 혹은 파봉에서의 유체입자의 속도가 파속을 초과하였을 경우를 쇄파로 정의하는 경우이다. 따라서, 쇄파시점의 정의에 따라 쇄파파고는 실험자료별로 약간 상이할 수 있다. 쇄파수심 역시 정수면(still water level, SWL)과 평균수면(mean water level, MWL)의 적용 여부에 따라 상이할 수 있다.
본 연구에서는 기존의 수리모형실험 결과에 대한 자료의 상당 부분을 Smith and Krasu(1991)의 연구로부터 취득하였으므로 Smith and Krasu(1991)가 제시하고 있는 파랑의 전면이 수직이 되는 시점을 쇄파로 정의하고 쇄파수심에는 정수면을 적용하였다. Fig. 1에 쇄파에 대한 물리량의 정의를 보인다. 그림에 보인 바와 같이 쇄파파고 Hb는 쇄파가 시작되는 시점의 파봉에서 파곡까지의 연직거리이며, 쇄파수심 hb은 바닥경사 m을 고려한 바닥으로부터 정수면까지의 연직거리이다.
2.2 실험자료의 수집기존의 쇄파에 관한 수리모형실험자료는 쇄파지표 예측에 관한 선행연구인 Lee et al.(2020)과 동일하게 Deo and Jagdale (2003), Lara et al.(2006) 및 Smith and Kraus(1990)의 연구를 참조하여 취득하였다. 또한, 본 연구에서는 추가로 Ishida and Yamaguchi(1983), Sakai et al.(1986) 및 Kakuno et al. (1996)의 연구로부터 실험결과를 추가로 획득하였다. 본 연구에서 이용한 실험자료의 조건 및 범위를 Table 1에 보인다.
기존 연구로부터 총 860개의 실험데이터를 획득하였으며 사면 경사는 0.01~0.2의 범위를 갖는다. 단, Ishida and Yamaguchi (1983)의 실험데이터는 쇄파수심에 대한 정보를 제공하고 있지 않고, 반면에 Xie et al.(2019)의 실험데이터는 각각 쇄파파고에 대한 정보를 제공하고 있지 않으므로 각각의 데이터는 쇄파파고와 쇄파수심을 예측하는 것으로 제한하였다. 한편, Table 1에서 *은 Smith and Kraus(1990)로부터 획득하였다.
2.3 쇄파지표에 대한 목표변수 설정쇄파의 크기를 기술하기 위해 쇄파파고와 쇄파수심과의 비 Hb/hb, 쇄파파고와 쇄파지점에서의 파장과의 비 Hb/Lb, 쇄파파고와 심해파고와의 비 Hb/Ho 그리고 쇄파파고와 심해파장과의 비 Hb/Lo 등의 쇄파 관련 지표가 제안되었으며, 이러한 쇄파지표 γb는 식(1)과 같이 사용되는 쇄파지표의 정의에 의해 바닥 경사 m 및 심해파형경사 Ho/Lo 등을 포함한 다양한 무차원 변수의 함수로 구성될 수 있다.
본 연구에서는 쇄파점에서의 파고와 수심을 예측하기 위한 입력변수 및 목표변수를 결정하기 위해 Table 1의 실험데이터에 대한 변수간의 상관관계를 먼저 고찰하였다.
Fig. 2는 쇄파파고와 쇄파수심과의 비 Hb/hb와 쇄파파고와 심해파고와의 비 Hb/Ho를 각각 심해파형경사 Ho/Lo의 함수로 도식한 결과이다. Fig. 2(a)와 (b)는 각각 McCowan-type 및 Munk-type의 쇄파파고지표에 해당하며 이에 기반한 많은 쇄파예측을 위한 경험식이 제안되어 왔다(Liu et al., 2011). 또한, 그림 중에 심해파형경사 Ho/Lo와 바닥경사 m 및 무차원 쇄파파고지표 사이의 피어슨 상관계수(PCC)를 산정하여 제시하였다. 피어슨 상관계수는 각 변수 간의 선형 상관관계를 나타내며, 일반적으로 상관계수의 절대값이 0.3~0.7일 경우 뚜렷한 선형관계, 0.7 이상일 경우는 강한 선형관계로 해석된다. Fig. 2로부터 쇄파파고와 쇄파수심과의 비 Hb/hb 및 쇄파파고와 심해파고와의 비 Hb/Ho는 심해파형경사 Ho/Lo와 뚜렷한 음적 선형관계를 가지고 있으며, 바닥경사 m과도 높은 양적 선형관계를 나타냄을 확인할 수 있다. 하지만, Fig. 2에서 적용한 쇄파파고지표는 상관계수가 0.7 이하로 강한 선형성을 갖고 있지 않으므로 선형회귀를 이용한 쇄파예측에 적절한 목표변수로 활용되기가 곤란하다.
Fig. 3은 Fig. 2와 유사하게 쇄파파고를 파장으로 무차원화시킨 Goda-type의 쇄파파고지표 Hb/Lo에 대해 심해파형경사의 함수로 도식한 결과이다. 또한 쇄파수심도 동일하게 파장으로 무차원화 한 쇄파수심지표 hb/Lo를 적용하였다. Fig. 3으로부터 확인되는 바와 같이 Hb/Lo 및 hb/Lo는 심해파형경사와의 상관계수는 0.9 이상으로 높은 선형 상관관계를 나타냄을 확인할 수 있다.
본 연구의 목표 중 하나는 쇄파지표 예측을 위한 새로운 선형식을 제안하는 것이므로 ML의 최종 예측을 위한 목표변수로 선형성이 높은 식(2)를 설정하였다.
여기서, Γb와 Ωb는 ML의 목표변수로 쇄파파고지표와 쇄파수심지표를 각각 나타내며, 목표변수는 바닥경사 m와 심해파형 경사 Ho/Lo의 함수이다.
3. 기계학습 기법 적용3.1 지도학습ML은 일정한 학습 알고리즘을 이용하여 주어진 자료를 스스로 분석 및 학습하고, 학습한 내용을 기반으로 새로운 자료에 대하여 분류하거나 값을 예측하는 것을 말한다. 즉, ML은 자료와 경험을 기반으로 학습을 통해 새로운 자료에 대한 예측성능을 개선하는 것이므로 ML에 있어서 학습은 매우 중요한 과정이다. ML의 학습방법에는 지도학습(supervised learning)과 자율학습(unsupervised learning)으로 구분할 수 있다. 지도학습은 정답이 있는 자료로부터 모델을 학습시키는 방법으로 대부분의 분류와 회귀문제는 지도학습의 범주에 해당한다. 반면, 자율학습은 자료의 주요 구성(특징) 관계를 파악하는 문제로 클러스터링(clustering)을 대표적인 예로 들 수 있다. 그 밖에도 상과 벌이라는 보상(reward)을 통해 현재의 상태에서보상이최대화되도록학습하는강화학습(reinforcement learning)이 있으며 주로 게임 프로그래밍에서 많이 활용되는 것으로 알려져 있다. 본 연구에서는 기존에 수행된 쇄파에 관한 실험자료를 바탕으로 쇄파지표를 예측하는 것이 목적이므로 지도학습 ML을 적용하였다. 이하에는 본 연구에서 적용한 ML 기법에 대하여 간략히 기술한다.
3.2 선형모델선형회귀모델(LRM)은 가장 간단한 ML 알고리즘 중의 하나이며, 예측할 목표변수(결과값)
여기서, w0는 상수항, wT = (w1, w2, …, wn)은 특징변수의 회귀계수 벡터이다. 입력값 x에 따른 결과값
여기서, n은 전체 데이터의 수, 위첨자 i는 데이터의 요소를 나타낸다.
위의 식과 같이 일반적인 LRM에서는 실제 결과값과 예측값의 평균제곱오차(mean squared error, MSE)가 최소화 되도록 학습이 이루어지기 때문에 학습에 적용한 훈련 데이터에 과대적합(over-fitting)이 발생하여 오히려 새로운 데이터 세트에서는 예측성능이 저하될 수 있다. 이를 방지하기 위해 회귀계수의 크기를 제어하여 과대적합을 개선하는 규제형 선형회귀모델(regularized LM)이 이용된다. 규제형 LRM에는 비용함수에 적용되는 수축 패널티(shrinkage penalty) 항에 따라 L2-norm을 적용하는 릿지회귀(ridge regression, RR), L1-norm을 적용하는 라쏘회귀(lasso regression, LR) 및 L1-norm과 L2-norm을 동시에 적용하는 엘라스틱 넷(Elastic Net, EN) 등이 있으나 본 연구에서는 규제형 LRM에는 회귀계수에 대한 L2-norm을 패널티 항으로 사용하는 식(5)의 릿지회귀를 적용하였다.
여기서, a는 사용자가 경험적으로 직접 조정되어야 하는 하이퍼 파라메터(hyper parameter)이다.
한편, LRM과 RR, LR, EN 등의 비용함수는 MSE를 사용하므로 예외적인 데이터인 이상값(outlier)에 따른 손실함수가 크게 증가한다. 반면, 평균절대오차(mean absolute error, MAE)는 MSE에 비해 이상점에 대한 영향이 상대적으로 작다. Huber(1964)에 의해 제안된 후버손실은 식(6)에 보인 바와 같이 일정 범위 ε을 기준으로 MSE와 MAE를 동시에 적용한다. 본 연구에서는 후버손실을 적용한 강건회귀(robust regression) 방법 중의 하나인 후버회귀(Huber regression, HR)를 사용하였다.
또한, 노이즈가 심한 입력 데이터로부터 회귀계수를 예측하는 방법인 란삭(random sample consensus, RANSAC) 알고리즘을 적용한 선형모델도 추가로 적용하였다. Fisher and Bolles(1981)가 제안한 RANSAC은 입력 데이터에 이상점(outlier)가 존재한다고 가정하고 무작위로 추출된 데이터의 집합에 대한 반복 학습을 통해 최적의 예측모델을 추출하는 방법이다. RANSAC에서 반복 학습의 횟수는 하이퍼 파라메터이며, 학습 알고리즘은 LRM을 이용하였다.
3.3 서포트 벡터 머신
Vapnik(1995)에 의해 제안된 서포트 벡터머신 (Support Vector Machine, SVM)은 분류나 회귀 및 이상값 감지에 사용하는 대표적인 지도학습 모댈 중의 하나이다. 일반적인 선형회귀모델에서는 MSE를 손실함수로 사용하므로 정상적인 데이터 분포로부터 이격된 이상값이 존재하는 경우, 이상점으로부터 발생하는 오차를 감소시키기 위해서는 낮은 오차를 갖는 정상적인 데이터(inlier)에도 영향을 미치게 되며, 결과적으로는 오차가 감소함에도 불구하고 모델의 예측성능이 저하되는 결과를 가져온다. SVM에서는 MSE를 적용하는 손실함수에서 발생하는 이러한 문제를 해결하기 위해 RR과 유사한 규제변수(regularization parameter)를 도입하며, 동시에 회귀계수의 L2-norm을 결합한 다음의 손실함수를 적용한다.
여기서, ξi ξi *는 Fig. 2에 보인 바와 같이 오차의 허용한계(margin) ± ε으로부터 벗어난 데이터들의 오차를 나타내는 여유변수(slack variable)이며, C는 과대적합과 일반화를 조절하는 규제변수로 C가 증가하면 과적합 가능성이 높아지며, 반대로 C가 감소하면 회귀계수의 L2-norm이 강조되어 일반화 기능을 갖는다.
오차의 한계치 ε과 규제변수 C는 식(5)~(6)에서 a와 유사하게 사용자에 의해 조정되어야 하는 하이퍼 파라메터이다. 또한, 식(7)의 손실함수는 다음과 같은 제약조건을 갖는다.
식(8)은 허용 한계치 ε을 벗어난 오차는 ξi + ε와 ξi * + ε보다 작은 오차를 가져야 하며, 오차의 절대값이 ε보다 작은 경우는 0이 되어야 함을 의미한다. 한편, SVM은 다양한 kernel 함수를 통해 비선형으로 확장할 수 있지만, 본 연구에서는 특징변수에 대한 회귀계수를 산정하기 위해 선형모델로 제한하였다.
4. 기계학습을 통한 쇄파지표 예측모델4.1 입력변수 및 교차검증ML의 입력변수는 쇄파지표와의 상관성이 높은 심해파형경사 Ho/Lo와 사면경사 m을 적용하여, 식(9)의 선형모델을 가정하였다.
여기서, wT = [w0, w1, w2]는 ML로부터 추정되는 회귀계수 벡터이다. 입력변수는 각각의 데이터에 대해 동일한 정도의 특성(분포) 스케일이 반영되도록 최소-최대정규화(Min-Max normalization) 혹은 z-점수정규화(z-score normalization) 등의 정규화 과정이 필요하지만, 본 연구에서는 선형모델에 기반한 ML으로부터 회귀계수를 산정하는 것이 목적이므로, 정규화를 수행하지 않은 원시 데이터를 적용하였다.
ML 모델을 학습시키기 위한 훈련 데이터(training data)는 Table 1에 보인 쇄파실험 데이터의 60%를 랜덤하게 적용하였으며, 나머지 30%의 데이터(test data)는 학습된 모델을 평가하는데 사용하였다. 하지만, 고정된 평가 데이터를 이용하여 ML의 성능을 판단하고 파라메터를 수정하는 경우에는 평가 데이터에 과대적합이 발생할 수 있다. 이러한 ML에서 발생 가능한 과적합을 방지하기 위해 교차검증(cross validation)을 적용하였다. 교차검증을 수행하는 경우에 보다 일반화된 모델을 구축할 수 있으며 제한된 데이터로 인한 과소적합(under-fitting)을 방지할 수 있는 장점이 있다.
교차검증에는 k-겹(k-fold), 리브-p-아웃(leave-p-out), 리브-원-아웃(leave-one-out), 계층별 k-겹(Stratified k-fold) 교차검증 등이 제안되어 있지만(Arlot and Celisse, 2010), 본 연구에서는 Fig. 5와 같이 교차검증에서 가장 일반적으로 사용되는 k-겹(k = 5) 교차검증을 적용하였다.
4.2 하이퍼 파라메터 최적화ML 모델의 예측성능을 향상시키기 위해서는 ML 알고리즘의 동작을 제어하는 하이퍼 파라메터에 대한 최적화 과정이 요구된다. 하이퍼 파라메터 최적화에는 사용자가 최적의 조합을 직접 찾아내는 Manual search, 파라메터에 대한 모든 조합으로부터 최적의 조합을 찾아내는 격자검색(Grid search) 및 하이퍼 파라메터의 적용 가능 범위 내에서 무작위로 반복 추출하여 최적의 조합을 찾아내는 무작위검색(Random search) 등의 방법이 있다(Bergstra and Bengio, 2012).
Fig. 6은 중요도가 높은 파라메터 3개와 중요도가 상대적으로 낮은 3개의 파라메터에 대한 9번의 최적화 시도에 대한 격자검색법과 무작위검색법의 차이를 보여준다. 격자검색이 무작위검색에 비해 9번의 최적화 시도가 2차원 공간 중에 균등하게 분포하여 균일한 검색범위를 제공한다. 반면에 격자검색은 중요 파라메터에 대해 단 3개 지점에서만 검색이 수행되지만, 무작위검색의 경우 9개 지점 모두를 검색할 수 있으므로, 중요 파라메터에 대해서는 훨씬 조밀하게 검색이 수행될 수 있는 장점이 있다. 하지만, 본 연구에서는 하이퍼 파라메터의 수가 제한적인 선형 ML 알고리즘을 적용하므로 검색이 단순한 격자검색을 적용하였다.
4.3 기계학습 API 적용사이킷런(Scikit-learn)은 파이썬(Python)으로 작성된 범용 머신러닝 라이브러리로 데이터 전처리, 모델의 구축 및 평가 등에 대한 다양한 애플리케이션 프로래밍 인터페이스(API)를 제공하고 있다(Pedregosa et al., 2011). 최근 들어 Tensorflow, Keras, Pytorch와 같은 딥러닝에 특화된 라이브러리가 다양한 분야에서 적극적으로 활용되고 있지만, 사이킷런은 분류와 회귀, 클러스터링, 차원축소와 같은 ML을 위한 검증된 알고리즘을 제공하고 있어 인공신경망을 이용한 딥러닝 이외의 ML 분야에서는 여전히 유용한 라이브러리로 인식되고 있다.
사이킷런에서 제공하는 모든 알고리즘은 2차원 배열(테이터 크기 × 특징)로 데이터가 입력되면, 추정 인터페이스(estimator interface)를 통해 입력된 훈련 데이터로부터 모델 파라메터의 학습이 이루어지며, 예측 인터페이스는 학습된 알고리즘을 이용하여 평가 데이터에 대한 예측을 수행한다. 본 연구에서도 사이킷런에서 제공하는 API를 이용하여 ML 알고리즘을 적용하였으며, 앞서 기술한 교차검증 및 하이퍼 파라메터 최적화를 위한 과정을 Fig. 7에 보인다.
4.4 쇄파지표 예측결과본 연구에서는 앞서 기술한 바와 같이 선형기반 모델의 ML 알고리즘인 LRM, RR, HR, RANSAC, SVM를 이용하여 쇄파지표를 예측하였다. ML 알고리즘의 예측성능 검토는 모델의 추정정도가 목표값을 표현하는 적합정도를 나타내는 다음의 결정계수 R2를 이용하였다.
여기서, xi는 목표값, yi는 예측값,
우선, 쇄파파고지표 Γb 예측을 위해 ML 알고리즘에 따른 회귀계수와 결정계수의 결과를 Table 2에 요약한다. 추정한 ML 모델이 목표변수를 추정하는 척도로 사용된 결정계수는 훈련데이터와 검증데이터를 각각 적용한 결과를 제시하였다. ML의 모델별로 결정계수는 하이퍼 파라메터에 따른 민감도가 상이함을 알 수 있다. L2-norm을 패널티 항으로 사용하는 RR의 경우 패널티의 강도를 조절하는 파라메터 a가 증가함에 따라 쇄파파고의 예측정도가 급격히 감소한다. 일정 범위 ε을 기준으로 MSE와 MAE를 동시에 적용하는 HR의 예측정도는 L2-norm에 따른 영향에 비해 ε에 보다 민감하며, ε이 증가함에 따라 결정계수가 미소하게 증가한다. RANSANC은 LRM을 기반으로 이상점 검색을 위한 무작위 반복계산의 횟수가 증가함에 따라 예측성능이 감소되는 결과를 보인다. 또한, SVM의 예측성능은 패널티 파라메터 C에 크게 의존하지 않음을 알 수 있다.
4.5 쇄파지표식 제안앞서 기술한 선형기반의 ML 알고리즘 중에 훈련 및 검증데이터에 대하여 양호한 예측성능을 보인 HR의 회귀계수를 이용하여 손쉬운 계산이 가능한 새로운 쇄파지표 산정식을 제안하였다. 쇄파파고 및 쇄파수심에 대한 산정식은 식(11)과 같다.
제안된 쇄파지표식은 선형식으로 바닥경사와 심해파형경사와의 함수로만 구성됨으로 매우 직관적으로 쇄파지표의 예측이 가능하다. 제안된 쇄파지표식의 검증을 위해 Rattanapitikon and Shibayama(2006)가 제안한 식(12)의 쇄파지표식과 예측성능을 비교하였다.
Fig. 9는 쇄파파고지표에 대한 식(11)의 제안식에 따른 계산 결과와 Rattanapitikon and Shibayama(2006)에 의해 제안된 식(12)의 계산결과를 각각 나타낸다. 그림 중에는 바닥경사에 따른 예측성능의 영향을 검토하기 위해 바닥경사를 세구간으로 구분하여 도식하였으며, 실험결과와의 오차 및 예측성능을 MSE와 결정계수로 표기하였다. 우선, Fig. 9(a)에 보인 본 연구에서 제한한 쇄파파고지표 산정식의 경우 Γb ≤ 0.01의 범위 및 상대적으로 완만한 바닥경사 m ≤ 0.02에서 실험결과를 과대평가하는 경향이 있으나 전체적으로 실험 결과를 양호하게 예측하고 있음을 알 수 있다. Fig. 9(b)의 Rattanapitikon and Shibayama(2006) 경험식은 Lee et al. (2020)이 지적한 바와 같이 상대적으로 완만한 사면경사에 대해 실험결과를 과대평가하고 있음이 확인된다. Fig. 9의 결과로부터 식(11) 및 식(12)의 쇄파파고지표에 대한 산정식 모두 결정계수 0.86 이상의 양호한 예측성능을 보이며, 본 연구에서 제안한 쇄파파고의 산정식이 1.4% 정도의 미소한 예측성능의 향상을 보였다. 단, 본 연구에서 제시한 쇄파파고지표에 대한 산정식은 Γb > 0.01의 범위에서 적용되어야 할 것으로 판단된다.
Fig. 10은 Fig. 9와 동일하게 쇄파수심지표에 대한 예측결과를 나타낸다. 쇄파수심에 대한 예측결과는 쇄파파고에 대한 예측결과와 유사한 경항을 보이고 있으며, 특히 바닥경사 완만한 m ≤ 0.02 범위에서 쇄파수심을 과대평가하고 있음을 알 수 있다. 또한, 본 연구에서 제시한 쇄파수심지표의 산정식이 기존의 경험식에 비해 5.4% 정도의 예측성능이 향상되었다. 따라서, Fig. 9와 Fig. 10으로부터 본 연구에서 제시한 쇄파지표의 제안식은 선형임에도 불구하고 기존의 경험식과 동일한 정도의 쇄파지표 예측이 가능함을 확인할 수 있다.
5. 결 론본 연구에서는 쇄파파고와 쇄파수심을 예측하기 위해 선형 모델과 서포트 벡터 머신(SVM)에 기반한 지도학습 머신러닝 알고리즘을 적용하였다. 쇄파지표의 산정을 위한 지도학습에는 기존에 발표된 쇄파 관련 실험데이터를 수집하였으며, 획득한 실험데이터의 60%를 이용하여 모델의 학습을 수행한 후에 나머지 40%에 대한 데이터를 이용하여 학습된 모델의 재현성을 평가하였다. 또한, 학습을 위한 특징변수에는 심해파형경사와 바닥경사를 사용하였으며, 학습과정에서 발생할 수 있는 과적합을 방지하기 위해 교차검증방법을 적용하였다. 학습된 모델별로 평가 데이터에 대한 예측성능을 평가하고, 학습된 결과를 바탕으로 특징변수에 대한 최적의 회귀계수를 추출하여 새로운 쇄파지표 산정식을 제안하였다. 본 연구에서 제안된 산정식을 이용한 쇄파파고 및 쇄파수심의 예측력은 결정계수가 각각 0.88과 0.86으로 기존 경험식에 비해 예측력이 다소 증가함을 확인하였다. 새로운 제안식은 선형식이므로 심해파형경사 및 바닥경사만으로부터 쇄파지표를 쉽게 산정할 수 있어 엔지니어링 실무에서 활용도가 높을 것으로 기대된다. 다만, 본 연구에서 제안한 쇄파지표 산정식은 비선형성을 고려하고 있지 않으므로 상대적으로 낮은 쇄파파고에 대한 낮은 예측성능을 보완할 수 있는 추가적인 연구가 필요할 것으로 판단된다.
감사의 글본 연구는 교육부와 한국연구재단의 재원으로 지원을 받아 수행된 사회맞춤형 산학협력 선도대학(LINC+) 육성사업 중 산학공동기술개발과제로 수행되었습니다. 연구 지원에 감사를 드립니다.
Fig. 2.Relationship between breaker index and deep water wave steepness by historical laboratory experiments. 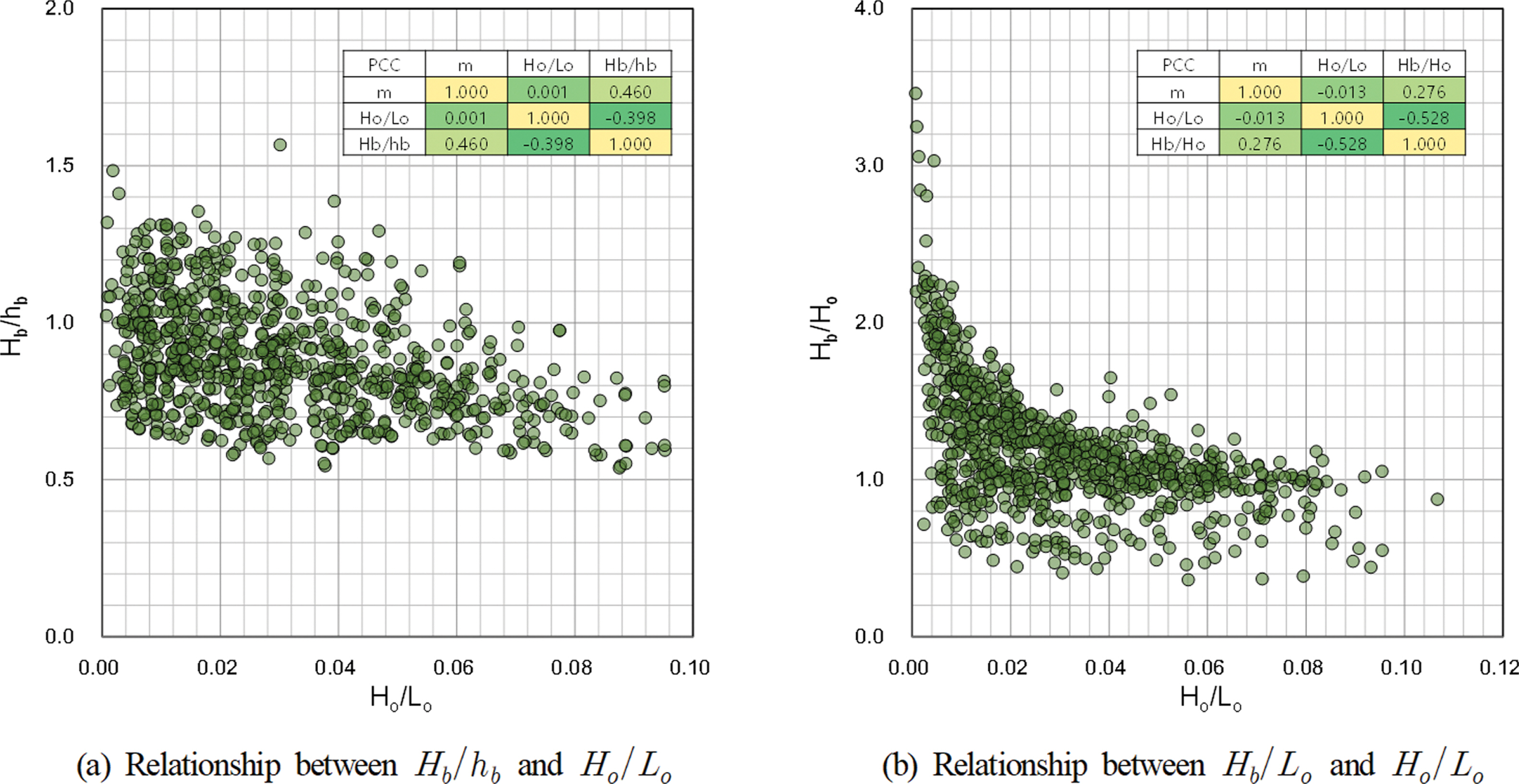
Fig. 3.Relationship between wave breaker index and deep water wave steepness by historical laboratory experiments. 
Fig. 6.Grid and random search of nine trials for hyper-parameter tuning (Bergstra and Bengio, 2012). 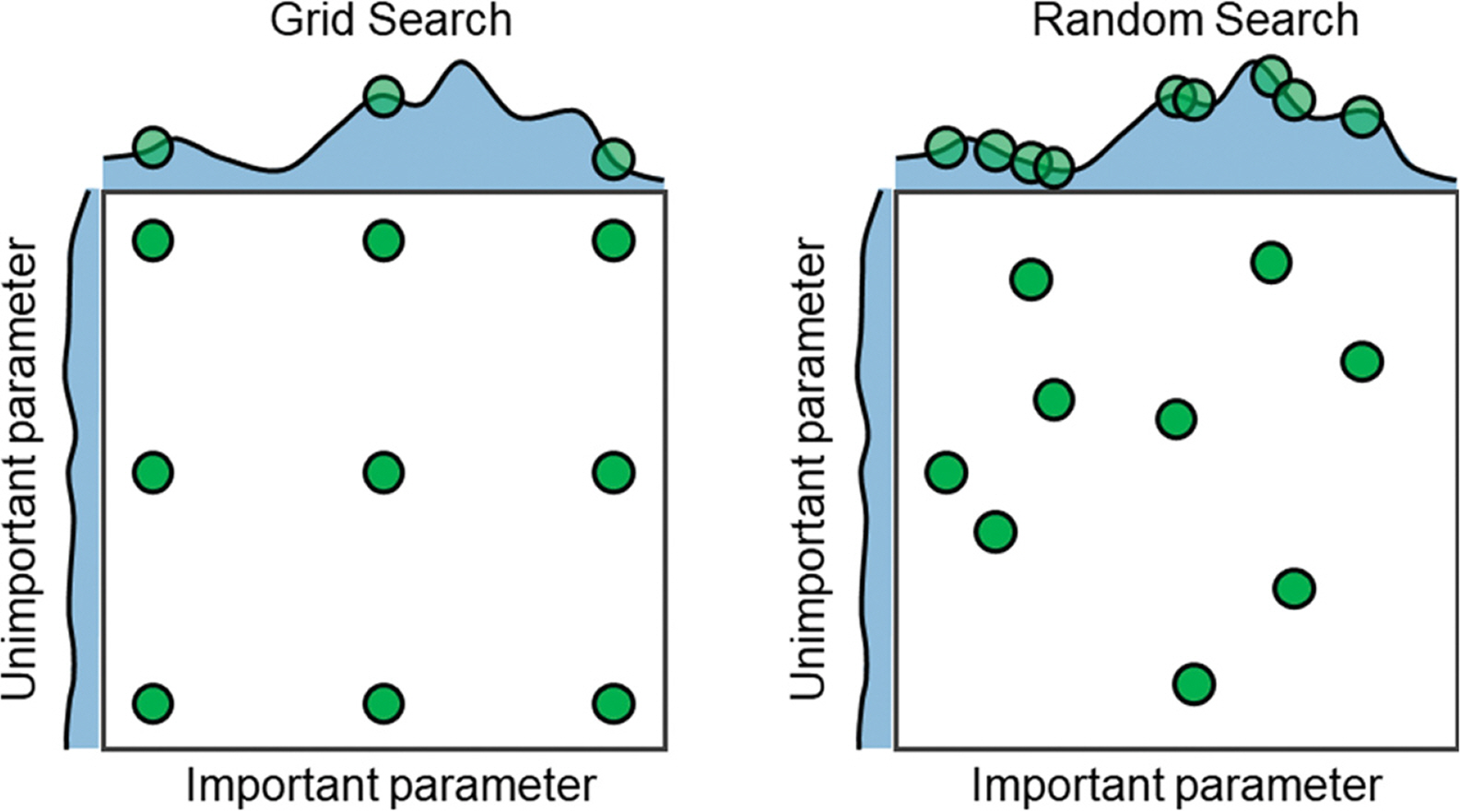
Table 1.Summary of historical experimental data set on breaking waves
Table 2.Summary of ML training and prediction results for breaking wave height Table 3.Summary of ML training and prediction results for breaking depth ReferencesArlot, S, Celisse, A (2010). A survey of cross-validation procedures for model selection, Static Surveys, 4, 40-79.
Bataineh, M., Marler, T (2017). Neural network for regression problems with reduced training sets, Neural Networks, 95, 1-9.
Bergstra, J., Bengio, Y (2012). Random search for hyper-parameter optimization, Journal of Machine Learning Research, 13, 281-305.
Buscombe, D., Carini, R.J., Harrison, S.R., Chickadel, C.C., Warrick, J.A (2020). Optical wave gauging using deep neural networks, Coastal Engineering, 155, 103593.
Bradford, S.F (2000). Numerical simulation of surf zone dynamics, Journal of Waterway Port Coastal and Ocean Engineering, 126, 1-13.
Chella, M.A., Bihs, H., Myrhaug, D., Muskulus, M (2015). Breaking characteristics and geometric properties of spilling breakers over slopes, Coastal Engineering, 95, 4-19.
Christensen, E.D (2006). Large eddy simulation of spilling and plunging breakwaters, Coastal Engineering, 53, 463-485.
Deo, M.C, Jagdale, S.S (2003). Prediction of breaking waves with neural networks, Ocean Engineering, 30, 1163-1178.
Etemad-Shahidi, A., Shaeri, S., Jafari, E (2016). Prediction of wave overtopping at vertical structures, Coastal Engineering, 109, 42-52.
Fisher, M.A., Bolles, R.C (1981). Random sample consensus: a paradigm for model fitting with applications to image analysis and automated cartography, Communications of the ACM, 24(6):381-395.
Formentin, S.M., Zanuttigh, B (2019). A Genetic Programming based formula for wave overtopping by crown walls and bull-noses, Coastal Engineering, 152, 103529.
Goda, Y (1970). A synthesis of breaker indices, Transactions of the Japan Society of Civil Engineers, 2(2):39-40.
Goda, Y (2010). Reanalysis of regular and random breaking wave statistics, Coastal Engineering Journal, 52(1):71-106.
Hieu, P.D., Katsutoshi, T., Ca, V.T (2004). Numerical simulation of breaking waves using a two-phase flow model, Applied Mathematical Modelling, 28, 983-1005.
Huber, P.J (1964). Robust Estimation of a Location Parameter, Annals of Mathematical Statistics, 35(1):73-101.
Ishida, H, Yamaguchi, N (1983). A theory for wave breaking on slopes and its application, Proceedings of 30th Japanese Conference on Coastal Engineering, JSCE, 34-38 (in Japanese)..
James, S.C., Zhang, Y., O’Donncha, F (2018). A machine learning framework to forecast wave conditions, Coastal Engineering, 137, 1-10.
Kakuno, S, Sugita, T, Goda, T (1996). Effects of wave breaking on entrainemnt of oxygen, a review, Proceedings of 43rd Japanese Conderence on Coastal Engineering, JSCE, 1211-1215 (in Japanese)..
Kazeminezhad, M.H., Etemad-Shahidi, A (2015). A new method for the prediction of wave runup on vertical piles, Coastal Engineering, 98, 55-64.
Kim, D.H., Kim, Y.J., Hur, D.S., Jeon, H.S., Lee, C (2010). Calculating expected damage of breakwater using artificial neural network for wave height calculation, Journal of Korean Society of Coastal and Ocean Engineers, 22(2):126-132.
Kim, D.H., Park, W.S (2005). Neural network for design and reliability analysis of rubble mound breakwaters, Ocean Engineering, 32, 1332-1349.
Kim, S.W., Suh, K.D (2011). Prediction of stability number for tetrapod armour block using artificial neural network and M5’ model tree, Journal of Korean Society of Coastal and Ocean Engineers, 23(1):109-117.
Lara, J.L., Losada, I.J., Liu, P.L.F (2006). Breaking waves over mild gravel slope: Experimental and numerical analysis, Journal of Geophysical Research, 111, 1-26.
Lee, J.S., Suh, K.D (2016). Calculation of stability number of tetrapods using weights and biases of ANN model, Journal of Korean Society of Coastal and Ocean Engineers, 28(5):277-283.
Lee, K.H., Kim, T.G., Kim, D.S (2020). Prediction of wave breaking using machine learning open source platform, Journal of Korean Society of Coastal and Ocean Engineers, 32(4):262-272.
Lee, K.H., Mizutani, N., Hur, D.S., Kamiya, A (2007). The Effect of groundwater on topographic changes in a gravel beach, Ocean Engineering, 34, 605-615.
Lin, P., Liu, P.L.F (1998). A numerical study of breaking waves in the surf zone, Journal of Fluid Mechanics, 359, 239-264.
Liu, Y., Niu, X., Yu, X (2011). A new predictive formula for inception of regular wave breaking, Coastal Engineering, 58(9):877-889.
McCowan, J (1984). On the highest wave of permanent type, Philosophical Magazine, 38(5):351-358.
Miche, R (1944). Mouvements ondulatoires de la mer en profondeur constante ou décroissante, Annales de Ponts et Chaussées, 114, 26-78 , 270–292, 369–406 (in French)..
Munk, W.H (1949). The solitary wave theory and its applications to surf problems, Annals of the New York Academy of Sciences, 51(3):376-462.
Oh, N.S., Jeong, S.T (2015). The Prediction of Water Temperature at Saemangeum Lake by Neural Network, Journal of Korean Society of Coastal and Ocean Engineers, 27(1):56-62.
Pedregosa, F., Varoquaux, G., Gramfort, A, Michel, V, Thirion, B, Grisel, O, Blondel, M, Prettenhofer, P, Weiss, R, Dubourg, V, Vanderplas, J, Passos, A, Cournapeau, D (2011). Scikit-learn: Machine Learning in Python, Journal of Machine Learning Research, 12, 2825-2830.
Rattanapitikon, W., Shibayama, T (2006). Braking wave formulas for breaking depth and orbital to phase velocity ratio, Coastal Engineering Journal, 48(4):395-416.
Ren, J (2012). ANN vs. SVM: Which one performs better in classification of MCCs in mammogram imaging, Knowledge-Based Systems, 26, 144-153.
Sakai, S, Kazumi, S, Ono, T, Yamashita, T, Saeki, H (1986). Study on wave breaking and its resulting entrainment of air, Proceedings of 33rd Japanese Conference on Coastal Engineering, JSCE, 16-20 (in Japanese)..
Samuel, A.L (1959). Some studies in machine learning using the game of checkers, IBM Journal of Research and Development, 3(3):210-229.
Smith, ER, Kraus, NC. (1990). Laboratory study on macro-features of wave breaking over bars and artificial reefs. U.S. Army Corps of Engineers Technical Report CREC-90-12, WES, p 232.
Stringari, D.L., Harris, D.L., Power, H.E (2019). A novel machine learning algorithm for tracking remotely sensed waves in the surf zone, Coastal Engineering, 147, 149-158.
Stokes, G.G (1880). Appendices and supplement to a paper on the theory of oscillatory waves, Mathematical and Physical Papers, 1, 219-229.
Vapnik, VN. (1995). The Nature of Statistical Learning Theory. Springer, New York.
Xie, W., Shibayama, T., Esteban, M (2019). A semi-empirical formula for calculating the breaking depth of plunging waves, Coastal Engineering Journal, 61(2):199-209.
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||