요약항 외곽시설 신뢰성 설계가 합리적으로 구현하기 위해서는 우리나라 해양환경 특성이 반영된 확률모형이 필요하며 이러한 시각에서 본 연구에서는 천 해역 확률모형 개발을 위한 기초연구의 일부로 불규칙 파랑 천수 과정을 수치 모의하였다. 수치 모의는 자연해안에서 흔히 관측되는 사주가 원빈에 형성된 해안을 대상으로 수행하였으며 파랑모형은 spatially filtered Navier-Stokes Eq., LES[Large Eddy Simulation], one equation dynamic Smagorinsky turbulence closure 등으로 구성하였다. 불규칙 파랑은 우리나라 동해안에서 관측되는 너울 특성을 반영하기 위해 다양한 첨두 증강계수를 지니는 JONSWAP 스펙트럼과 random phase method를 사용하여 모의하였다. 파고분포의 모수는 먼저 수치 모의에서 관측된 자유수면 시계열 자료를 threshold crossing method로 파별 해석[wave by wave analysis]하여 개별 파랑을 특정하고, 이어 이렇게 특정된 파마루와 파곡 빈도 해석결과로부터 산출하였다. 모의결과 현재 천 해역 파고분포를 대표하는 수정 Glukhovskiy 파고분포는 큰 파고와 작은 파고 발생확률은 과다하게, 중간 크기 파고 발생확률은 과소하게 평가하는 것으로 모의 되었으며, 이에 반해 본 논문에서 제시된 파고분포의 경우 일치도가 상당하였다. 또한, 전술한 수정 Glukhovskiy 파고분포와의 간극은 쇄파역에서 제일 현저하게 관측되어 수정 Glukhovskiy 파고분포를 쇄파역 언저리에 거치되는 외곽시설 신뢰성 설계에 적용하는 일은 지양되어야 할 것으로 판단된다.
AbstractIn order to make harbor outskirt facilities robust using the reliability-based design, probabilistic models of wave heights at varying stage of shoaling process optimized for Korean sea waves are prerequisite. In this rationale, we numerically simulate the nonlinear shoaling process of random waves over the beach with a sandbar at its foreshore. In doing so, comprehensive numerical models made of spatially filtered Navier-Stokes Eq., LES [Large Eddy Simulation], dynamic Smagorinsky turbulence closure were used. Considering the characteristics of swells observed at the east coast of Korean Peninsula, random waves were simulated using JONSWAP wave spectrum of various peak enhancement coefficients and random phase method. The coefficients of probabilistic models proposed in this study are estimated from the results of frequency analysis of wave crests and its associated trough detected by Wave by Wave Analysis of the time series of numerically simulated free surface displacements based on the threshold crossing method. Numerical results show that Modified Glukhovskiy wave height distribution, the most referred probabilistic models at finite water depth in the literature, over-predicts the occurring probability of relatively large and small wave heights, and under predicts the occurrence rate of waves of moderate heights. On the other hand, probabilistic models developed in this study show vary encouraging agreements. In addition, the discrepancy of the Modified Glukhovskiy distribution from the measured one are most visible over the surf zone, and as a result, the Modified Glukhovskiy distribution should be applied with caution for the reliability- based design of harbor outskirt facilities deployed near the surf-zone.
1. 서 론최근 항 외곽시설은 기존의 결정론적 설계에서 벗어나 신뢰성 설계로 이행되고 있으며, 이러한 추이는 결정론적 설계 과정에서 수행되는 주관적 판단을 배제함으로써 합리적 설계를 가능하게 하는 신뢰성 설계의 구조적 장점에 기인한다(PIANC, 1992). 전술한 신뢰성 설계의 장점이 구현되기 위해서는 항 외곽시설에 작용하는 외력과 내구성을 가늠하는 파랑이라는 무작위 사상에 대한 확률모형이 필요하며, 현재 문헌에서 빈번하게 언급되는 파고분포를 정리하면 다음과 같다.
Rayleigh 파고분포는 현재 해안공학 계에 가장 널리 알려진 확률모형으로, 선형모형임에도 불구하고 심해 불규칙 파랑의 경우 일치도가 상당하다(Longuet-Higgins, 1952). 그러나 항 외곽시설이 거치되는 수심이 유한한 해역의 경우 천수, 굴절 등과 같은 변형으로 인해 파랑의 비선형성은 무시할 수 없을 정도로 증가하여 파고분포는 상당한 변화를 겪는다(Choi and Cho, 2019).
이러한 유한 수심에서의 파고분포로는 Glukhovskiy(1966)에 의해 처음 제시된 이래, 초기 모형이 지니는 모수 산정의 불확정성(Battjes, 1986)이 Klopman and Stive(1989), Klopman(1996) 등에 의해 해결되는 등 꾸준히 개선된 수정 Glukhovskiy 분포가 현재 대표적인 천해역 파고 분포로 보인다(Choi and Cho, 2019). 그러나 수정 Glukhovskiy 분포는 천수의 마지막 단계인 쇄파역에서는 상당히 보수적인 값을 주며(van Vledder et al., 2013), Battjes and Groenendijk(2000)는 전술한 단점을 개선하기 위해 파고 표본 공간을 두 개로 분리하여 쇄파로 야기되는 파고 감쇄를 설명한 복합 Weibull 파고분포를 제시한 바 있으며, 이후 Battjes와 Groenendijk의 복합 Weibull 분포는 대표적인 쇄파역 파고 분포로 선호된다(Choi and Cho, 2019).
우리나라를 둘러싼 해양환경은 분명히 미국 혹은 유럽의 그것과는 상당한 구조적 차이를 지니며, 이러한 차이는 반시계 방향으로 비스듬히 틀어진 형상으로 파랑 발달에 필요한 충분한 취송거리가 제한적인 방위에서만 확보되는 동해에서 확연하게 드러난다(Cho et al., 2019; Chang and Cho, 2019). 이러한 차이로 인해 우리나라 동해안에서는 장주기의 너울이 우세한 미국과는 달리 상당히 다양한 주기의 너울이 관측되며 이러한 파랑특성은 해안구조물의 피로 거동에 상당한 영향을 미칠 수 있다(Cho and Kim, 2019; Park and Cho, 2019). 이러한 구조적 차이에도 불구하고 아직 여명기에 불과한 우리나라 신뢰성 설계는 전술한 미국 혹은 유럽에서 선호되는 확률모형을 단순 수용하여 진행된 것으로 보이나 이러한 관행은 상당한 오류를 초래할 수 있어 전술한 확률모형에 우리나라 해양환경 특성을 담아내려는 노력이 필요하다(Kim et al., 2005, 2009; Suh et al., 2003). 최근 이러한 시각에서 우리나라 해양환경에 최적화된 확률모형을 개발하려는 노력이 Choi and Cho(2019)에 의해 수행되어 수심이 20 m 내외인 울산 전면해역에서의 파고분포 등이 개발되는 등 성과가 상당하다.
최근 대형화되는 선박으로 인해 무역항의 경우 항 외곽시설은 수심이 25 m 내외의 해역에 거치되나, 소규모 어항의 경우 외곽시설의 상당 부분은 여전히 수심이 5m 내외인 천해역에 거치되기 마련으로 소규모 어항 신뢰성 설계를 구현하기 위해서는 천수와 천수 최종단계에서 진행되는 쇄파를 반영한 천해역 확률모형 개발이 시급해 보인다. 그러나 우리나라의 경우 WINK(Jeong et al., 2018)에서 확인할 수 있듯 확률모형 개발에 필요한 장기 천해역 파고 관측자료가 가용하지 않은 경우가 대부분으로 본 논문에서는 장기 천해역 파고 관측자료의 부재로 인한 어려움을 해결하기 위해 불규칙 파랑의 천수 과정을 수치 모의하였다. 수치 모의는 아직 개발의 손길이 미치지 못해 자연해안의 여러 성정을 지니는 우리나라 동해안 맹방 해빈 관측자료를 토대로 원빈 해역에 사주가 형성된 해안을 대상으로 수행되며, 이 과정에서 파랑모형은 spatially filtered Navier-Stokes Eq., LES[Large Eddy Simulation], one equation dynamic Smagorinsky 난류모형으로 구성하여 관측자료에 버금가는 정도의 수치 모의가 가능하도록 노력하였다(Cho, 2020a, 2020b).
이해를 돕기 위해 2.1, 2.2, 2.3절에는 각각 Rayleigh 파고분포, 수정 Glukhovskiy 파고분포, 복합 Weibull 파고분포를 정리하였으며, 2.4절에는 우리나라 해양환경에 최적화된 파고 확률모형을 정리하였다. 3장, 4장에는 각각 파랑모형과 turbulence closure, 수치 모의를 다루며, 수치 결과는 5.1 불규칙 파랑의 비선형 천수 특성, 5.2 천수 단계별 파고분포, 5.3 천수 단계별 파고·주기 결합분포로 나누어 정리하였다.
2. 파고분포2.1 Rayleigh 분포Rayleigh 파고분포 FH(h)를 유의 파고 HS를 중심으로 기술하면 다음과 같으며(Longuet-Higgins, 1952),
여기서 P[H < h]는 불규칙 파고 H가 h 보다 작은 확률을 나타낸다.
2.2 수정 Glukhovskiy 분포수정 Glukhovskiy 파고 분포함수 FH(h)를 기술하면 다음과 같으며,
여기서 A와 κ는 수정 Glukhovskiy 파고 분포함수의 모수로
수정 Glukhovskiy 파고 분포함수를 확률밀도함수
식(2)에 정의된 수정 Glukhovskiy 파고 분포함수는 먼바다[d→∞]에서는 Rayleigh 분포로 수렴되는 것을 알 수 있다.
2.3 복합 Weibull 분포복합 Weibull 파고분포함수(cumulative distribution function)
파고분포함수의 미분으로 정의되는 확률밀도함수
여기서
식(8)에서 d는 수심, α는 해저면 경사를 각각 나타낸다. 식(7), (8)에서 알 수 있듯 복합 Weibull 분포함수의 구체적 형태를 결정하는 것은 κ1, κ2,
2.4 우리나라 해양환경에 최적화된 파고 확률모형최근 Choi and Cho(2019)는 JMA[Japan Meterological Agency]와 NOAA[National Oceanic and Atmospheric Administration]의 해상풍 자료와 SWAN에 기초하여 2003년 1월 1일부터 2017년 12월 31일까지 한 시간 간격으로 역추산 된 울산 전면해역에서의 유의 파고와 첨두 주기를 활용하여 우리나라 해양환경에 최적화된 확률모형을 유도한 바 있다. 이 연구에서 Choi and Cho(2019)는 전술한 유의 파고 시계열 자료로부터 최소 자승법을 활용하여 장기 유의 파고 확률분포를 도출하였으며, 모의결과 그동안 선호되던 삼 변량 Weibull 분포보다는 수정 Glukhovskiy 분포 계열에서 일치도가 가장 우월한 것으로 드러났다.
Choi and Cho(2019)에 의해 유도된 수정 Glukhovskiy 분포 계열 파고 확률밀도함수 fH(h)는 다음과 같이 정의되며,
이를 분포함수로 기술하는 경우 다음과 같다.
Choi and Cho(2019)에 의하면 식(10)에 정의된 수정 Glukhovskiy 분포의 모수 Ap, Hp, κp는 신뢰수준 95%에서 각각 Ap = 15.92, Hp = 4.374 m, κp = 1.824의 값을 지닌다.
3. 수치모형3.1 파랑모형수치 모의는 spatial averaging filter를 활용하여 차용된 격자보다 작은 규모의 난류는 등방성에 근접한다는 시각에서 LES[Large Eddy Simulation], 잔차 응력[residual stress]은 one equation dynamic Smagorinsky 난류모형을 활용하여 수행하였다. 이 과정에서 파랑모형은 spatially filtered Navier-Stokes Eq.과 질량 보존 식으로 구성하였으며 자유수면은 VOF(Volume Of Fraction) 법을 활용하여 추적하였다. 전술한 수치모형은 Cho(2020a, 2020b) 등에 의해 Cnoidal waves의 천수 과정과 경계층 streaming, beach cusp 쇄파역에서의 경계층 streaming을 수치해석하는 과정에서 충분한 검증 과정을 거친 것으로 보인다.
파랑모형은 Navier-Stokes 방정식에 spatial averaging filter를 적용하여 유도되며, 이렇게 얻은 운동량 방정식과 연속방정식은 각각 다음과 같이 기술될 수 있다.
식(12)에서 ρ는 물의 밀도, v = μ/ρ는 동 점성계수,
식(13)의 우측 오른쪽 3개 항은 여과 과정[spatial averaging]에서 발생하는 잔차 응력[residual stress]을 나타낸다. 전술한 잔차 응력을
여기서 δij는 Kronecker delta, ksgs는 sub-grid scale의 운동에너지를 각각 나타내며 ksgs는 다음과 같이 기술될 수 있다.
이상(二狀) 유체 해석을 위한 VOF 식을 기술하면 다음과 같으며,
여기서 γ는 단위 격자 체적에서 물이 차지하는 비율을 나타내는 VOF 계수로 1에 가까울수록 액체상태, 0에 가까울수록 기체 상태를 나타내며 본 논문에서는 자유 수면의 위치를γ = 0.5로 정의하였다.
3.2 One-equation dynamic Smagorinsky turbulence closure
식(17)에 기술된 지배방정식을 완결하기 위해서는 여과 과정에서 발생한 비등방성 잔여 응력 항을 모형화할 필요가 있으며 문헌에서 자주 언급되는 Smagorinsky(1963) 모형을 기술하면 다음과 같다.
여기서 νsgs는 잔여 유속의 난류 점성계수,
식(19)에서 난류 점성계수 νsgs는 다음과 같이 정의되며,
여기서 CS는 Smagorinsky 계수로 일반적인 전단 흐름의 경우 0.065-0.1 사이의 값을 지니며, 본 논문에서는 0.094를 사용하였다.
식(21)에서 쇄파역에서의 난류 에너지의 국지적 생성, 확산, 소산은 ksgs에 대한 이송방정식을 추가로 도입하는 경우 설명될 수 있으며 ksgs 이송방정식을 기술하면 다음과 같다(Yoshizawa and Horiuti, 1985).
식(22)에서 Cε는 경험계수, ∆ = (∆x∆y∆z)1/3, ∆x, ∆y, ∆z는 각 방향에서의 필터 크기를 나타내며, 난류 에너지의 생성을 의미하는
식(23)에서
4. 수치 모의현재 우리나라의 경우 확률모형 개발에 필요한 장기 천해역파고 관측자료가 가용하지 않는 경우가 대부분으로 장기 천해역 파고 관측자료의 부재로 인한 어려움을 해결하기 위해 원빈에 사주가 형성된 해안을 대상으로 불규칙 파랑 천수 과정을 수치 모의하였다. 수치 모의에 사용된 수치 수조는 Fig. 1에 도시하였으며 도시된 계산영역은 312,000(520 × 10 × 60)개의 절점을 사용하여 이산화하였으며 바닥에는 no-slip boundary condition, 측면에는 periodic boundary condition을 적용하였다.
해안선으로부터 60~80 m 이격된 지점까지 경사가 1/10 내외인 급경사의 전 빈이 포진하며 이후 수심이 6 m 내외인 간조 단구[low tide terrace]가 넓게 포진하는 동해안 지형 특성과 과도한 계산량을 피하고 보다 효율적인 수치 모의를 위해 수심은 0.6m로 선정하였으며, 이는 1/10 Scale에 해당한다. 불규칙 파랑은 JONSWAP 스펙트럼과 random phase method(Frigaard and Anderson, 2010)를 사용하여 모의하였으며 JONSWAP 스펙트럼을 기술하면 다음과 같다.
식(25)에서 ω = 2π/f, f는 주파수[Hz], γ는 첨두 증강계수, αp는 Phillips 계수, ωp는 첨두 각 주파수를 나타내며 각각 다음과 같이 기술될 수 있으며,
여기서 U10는 고도 10 m에서의 풍속, LF는 취송 거리를 각각 나타내며, Fig. 2에는 풍속에 따른 유의 파고와 주기의 변화를 정리하였다.
실 해역의 경우 γ는 1~6 사이, αp는 0.0081~0.1 사이에 분포한다. γ와 αp가 각각 1과 0.0081의 값을 지니는 경우는 완전히 발달한 풍성 파에 해당하며 조파 수조에서는 이보다 큰 값이 관측된다. σ는 band width parameter를 나타내며 다음과 같이 정의된다.
우리나라 동해안의 경우 반시계방향으로 틀어진 형상의 동해에 노출되어있어 파랑 발달에 필요한 충분한 취송거리가 확보되는 방위가 한정되는 지형 특성으로 다양한 주기의 너울이 관측되며, 이러한 너울의 점유율은 80%를 상회한다(Cho and Kim, 2019). 너울의 성격은 생성과정과 이송 이력에 의해 결정되며, 따라서 너울 스펙트럼의 보편적 형태는 특정할 수 없다는 의견이 다수를 이루나, 풍속이 잦아들면 너울의 군속도는 풍속을 상회하므로, 대기의 에너지가 해수로 유입될 수 없다. 또한, 단주기파랑은 느린 파속으로 파군으로부터 분리되어 후행하여, 파랑에너지는 첨두 주파수 인근에 집중된다. 이상의 논의를 토대로 첨두 주파수 인근 협대역에 파랑에너지가 집중되는 너울의 특성을 고려하여 본 논문에서는 첨두 증강계수를 γ = 3.3으로 취하였으며[Fig. 3 참조], 또한 비교를 위해 γ = 1.0인 경우에 대해서도 수치 모의를 수행하였다.
이렇게 선정된 스펙트럼은 팔백 개의 성분 파 [∆f = 0.02 Hz]로 구성된 불규칙 파랑으로 모의하였으며 이 경우 첫 번째 성분 파의 주기는 T = 50 s로 외 중력파로 분류할 수 있으며 이를 Scale이 1/10인 모형에서의 값으로 환산하는 경우 Tm = 15.81 s에 해당한다.
5. 수치 결과5.1 불규칙 파랑의 비선형 천수 특성
Fig. 4에는 RUN 1[γ = 3.3]과 RUN 2[γ = 1.0]에서 관측된 자유수면 snapshot을 도시하였다. 첨두 증강계수가 큰 RUN 1에서 Run 2보다 상대적으로 큰 파랑이 조파되어 정연하게 해안으로 진행되는 것을 확인할 수 있으며, 사주 정점에서는 plunging 형태의 쇄파가 진행되는 것을 관측할 수 있다[Fig. 4(a) 참조].
Fig. 5에는 RUN 1과 RUN 2에서 Gauge 1, 2, 3, 4, 5 [Fig. 1 참조]에서 관측되는 자유수면 시계열 자료를 도시하였다. RUN 1의 경우 t = 110 s에서 관측되는 파고 0.4 m의 큰 파랑이 이채롭다[Fig. 5(a) Gauge 1 참조]. 전술한 파고는 수심의 66%에 달하며 쇄파 한계치로 알려진 79%를 밑돈다는 점에서 물리적으로 가능하며 낮은 파곡과 첨예한 파 마루 등 비선형 파랑의 전형적인 성정을 지닌다. 전술한 파랑은 전파과정에서 진폭분산으로 인해 파 전면부는 가파르게, 파 후면부는 완만하게 변형되는 것을 관측할 수 있다[Fig. 5(a)Gauge 2 참조].
이에 반해 RUN 2에서는 파고는 작으나 상대적으로 큰 대역폭으로 인해 장주기 파랑이 조파되어 평균 해면이 완만하게 변조하는 것이 흥미롭다[Fig. 5(b) Gauge 1, 2 참조].
Fig. 6(a)에는 RUN 1에서 [u, w]로 구성된 위상공간에서 유속 벡터가 t = 296.8~300.1 s에 걸쳐 z = 0.562m 평면에서 그리는 궤적을 도시하였다[Gauge 3]. 상당히 다양한 성격의 파랑이 섞여 있는 것을 확인할 수 있다는 점에서 목표했던 불규칙 파랑이 상당한 정도로 모의 된 것으로 판단된다. 이 밖에 천수와 이로 인해 강해진 성분 파랑 간의 공진성 상호작용으로 생성된 고차 조화성분으로 인해 해안 방향 흐름 강도가 먼바다 방향 흐름 강도보다 우월한 비선형 파랑의 대표적인 성정도 찾아볼 수 있으며, 해안 방향 흐름의 점유율은 58%로 먼바다 방향 흐름 점유율 42%를 16% 상회한다[Fig. 6(b) 참조]. Fig. 7에는 RUN 1에서 관측되는 쇄파역에서의 자유 수면과 유선을 차례대로 도시하였다. 파 마루 사이의 간격이 일정하지 않다는 점에서 목표했던 불규칙 파랑이 상당한 정도로 모의 된 것을 다시 한번 확인할 수 있다. 또한, 사주 down-wave side에서 형성되는 vortex tube를 유선에 의해서 특정할 수 있으며, 이렇게 형성된 vortex tube가 해안 방향으로 이행되는 과정을 확인할 수 있다. 이 밖에 쇄파 시 저면 인근에서 관측되는 vortex tube가 이채롭다[Fig. 7(a) 참조].
Fig. 8에는 RUN 2에서 관측되는 유속 벡터를 차례대로 도시하였으며 처오름 과정에서 유속이 상당한 세기라는 것을 확인할 수 있다.
Fig. 9, 10에는 불규칙 파랑이 천수 과정에서 겪는 변화를 더욱 자세히 살펴보기 위해 Gauge 1, 2, 3, 4, 5[Fig. 1 참조]에서 관측된 자유수면 시계열 자료로부터 산출한 파랑 스펙트럼을 도시하였다. 이미 진행된 천수로 Gauge 2에서의 스펙트럼은 상대적으로 짧은 주기와 긴 주기 파랑의 진폭이 증가하는 것을 확인할 수 있다. 이러한 성정은 풍성파 성장 과정을 다룬 Hasselmann(1967), Phillips(1980) 연구성과 이후 해안공학 계에서 널리 알려진 비선형 sub-harmonic resonance interaction의 일반적 거동특성에서도 확인할 수 있다. 사주의 정점에 해당하는 Gauge 3에서의 스펙트럼은 긴 주기의 파랑도 바닥의 영향을 느끼기 시작하여 진폭은 증가하였으며, 중간 크기[0.1 < ω < 0.15] 파랑의 진폭은 감소하였다. 전빈 깊숙이 거치된 Gauge 4의 경우 전 주파수 대역에서 진폭이 증가하는 것으로 보이며, 해안 가까이 거치된 Gauge 5의 경우 이미 진행된 쇄파로 인해 장주기에 해당하는 0.025 < ω < 0.125 대역에서 진폭이 상당량 감소하는 것을 확인할 수 있다.
5.2 천수 단계별 파고분포
Fig. 11에는 먼저 Gauge 1, 2, 3, 4, 5에서 관측된 자유수면 시계열 자료를 threshold crossing method로 파별 해석[Wave by Wave Analysis]하여 개별 파랑을 분리하고 이어 이렇게 특정된 파 마루와 파곡을 삼차 spline method로 보간하여 산출한 wave envelope process를 도시하였다. 상당히 정도로 파 마루와 파곡이 특정되는 것을 확인할 수 있어 향후 진행되는 파고분포, 파고와 주기 결합확률 분포해석에 대한 신뢰성은 충분히 확보된 것으로 판단된다.
Fig. 12에는 이렇게 얻은 파고 빈도해석 결과를 정리하였으며, 비교를 위해 현재 천해역 파고분포를 대표하는 수정 Glukhovskiy 파고분포도 함께 수록하였다. Fig. 13, 14에는 파고분포 별 차이를 더욱 확연히 드러내기 위해 전술한 파고 분포를 log-log scale에서 도시하였다. Fig. 12, 13, 14에서 알 수 있듯, 수정 Glukhovskiy 파고분포는 큰 파고와 작은 파고 발생확률은 과다하게, 중간 크기의 파고 발생확률은 과소하게 평가하는 것으로 보이나 본 논문에서 제시된 파고분포의 경우 일치도가 상당하다[Fig. 13, 14 참조]. 또한, 전술한 수정 Glukhovskiy 파고분포와의 간극은 해안에 가까우며 쇄파가 진행된 Gauge 5에서 제일 현저하게 관측되므로 수정 Glukhovskiy 파고분포를 쇄파역 언저리에 거치되는 외곽시설 신뢰성 설계에 적용하는 일은 지양되어야 할 것으로 판단된다[Fig. 14 Gauge 5 참조].
5.3 천수 단계별 파고·주기 결합분포
Fig. 15, 16에는 RUN 2 Gauge 1, 2, 3, 4, 5에서 관측된 자유수면 시계열 자료를 threshold crossing method로 파별 해석[Wave by Wave Analysis]하여 얻은 파고와 주기 결합 확률 분포를 천수 단계별로 정리하였다. 천수가 시작되면서 상당한 확률 질량이 큰 파고로 이동하는 것을 확인할 수 있으며[Fig. 15(b) 참조], 사주 정점에서는 공진성 wave-wave interaction으로 장주기 파랑의 발생확률이 현저히 증가하는 것으로 알 수 있다[Fig. 15(c) 참조]. 이차 천수가 시작되는 Gauge 4의 경우 확률 질량이 큰 파고와 긴 주기 영역으로 이동하는 것으로 보이며[Fig. 15(d) 참조], 쇄파가 진해 중인 Gauge 5의 경우 파고가 전체적으로 감소하나 wave-wave interaction으로 생성된 장주기의 파랑[infra-gravity waves, 외중력파]은 에너지 감쇄가 비교적 적은 surging 형태의 쇄파로 인해 파고 감소는 미미해 보인다. 전술한 천수 단계별 파고와 주기 결합확률 분포 변화추이는 RUN 1[γ = 3.3]에서도 유사하게 관측할 수 있다[Fig. 16 참조].
6. 결 론우리나라를 둘러싼 해양환경은 분명히 미국 혹은 유럽의 그것과는 상당한 구조적 차이를 지니며, 이러한 차이는 반시계방향으로 비스듬히 틀어진 형상으로 파랑 발달에 필요한 충분한 취송거리가 제한된 방위에서만 확보되는 동해에서 확연하게 드러난다. 이러한 차이로 인해 우리나라 동해안에서는 장주기의 너울이 우세한 미국과는 달리 상당히 다양한 주기의 너울이 관측된다. 이러한 구조적 차이에도 불구하고 아직 여명기에 불과한 우리나라 신뢰성 설계는 미국 혹은 유럽에서 선호되는 확률모형을 단순 수용하여 진행되는 것으로 보이나 이러한 관행은 상당한 오류를 초래할 수 있어 전술한 확률모형에 우리나라 해양환경 특성을 담아내려는 노력이 필요해 보인다.
이러한 시각에서 본 논문에서는 신뢰성 설계 합리적 구현에 필요한 천해역 확률모형 개발을 위한 기초연구의 일부로 불규칙 파랑의 천수 과정을 수치 모의하였다. 수치 모의는 자연 해빈에서 흔히 관측되는 사주가 원빈에 형성된 해안을 대상으로 수행하였으며 이 과정에서 파랑모형은 spatially filtered Navier-Stokes Eq., LES[Large Eddy Simulation], one equation Dynamic Smagorinsky turbulence closure로 구성하여 관측자료에 버금가는 정도의 수치 모의가 가능하도록 노력하였다.
불규칙 파랑은 우리나라 동해안에서 관측되는 너울 특성을 고려하여 다양한 첨두 증강계수를 지니는 JONSWAP 스펙트럼과 random phase method(Frigaard and Anderson, 2010)를 사용하여 모의하였다. 파고분포의 모수는 수치 모의에서 관측된 자유수면 시계열 자료를 threshold crossing method로 파별 해석[Wave by Wave Analysis]하여 얻은 파 마루와 파곡 빈도 해석결과를 least square method로 산출하였다. 모의결과 현재 천해역 파고분포를 대표하는 수정 Glukhovskiy 파고분포는 큰 파고와 작은 파고 발생확률은 과다하게, 중간 크기의 파고 발생확률은 과소하게 평가하는 것으로 모의 되었으며 본 논문에서 제시된 파고분포의 경우 일치도가 상당하였다. 또한, 전술한 수정 Glukhovskiy 파고분포와의 간극은 해안에 가까우며 쇄파역에서 제일 현저하게 관측되므로 수정 Glukhovskiy 파고분포를 쇄파역 언저리에 거치되는 외곽시설 신뢰성 설계에 적용하는 일은 지양되어야 할 것으로 판단된다.
불규칙 파랑이 천수 과정에서 겪는 변화를 더 자세히 살펴보기 위해 수치 모의에서 관측된 자유수면 시계열 자료로부터 천수 단계별 파랑 스펙트럼 산출도 병행하여 수행하였다. 천수가 시작되면서 상대적으로 짧은 주기와 긴 주기 파랑의 진폭이 증가하는 것을 확인하였다. 이러한 성정은 풍성파 성장 과정을 다룬 Hasselmann(1967), Phillips(1980) 연구성과 이후 해안공학 계에서 널리 알려진 비선형 sub-harmonic resonance interaction의 일반적 거동특성에서도 확인된다는 점에서 목표했던 불규칙 파랑이 상당한 정도로 모의 된 것을 확인할 수 있었다.
파고 주기 결합분포의 경우 천수가 시작되면서 상당한 확률 질량이 큰 파고로 이동하였으며, 사주 정점에서는 공진성 wave-wave interaction으로 장주기 파랑의 발생확률이 현저하게 증가하는 것을 확인하였다. 사주 내측 해안에서 이차 천수가 시작되면서 확률 질량이 큰 파고와 긴 주기 영역으로 이동하였으며, 쇄파역에서는 쉽게 예상해 볼 수 있듯 파고가 전체적으로 감소하나 wave-wave interaction으로 생성된 장주기의 파랑[infra-gravity waves]의 경우 에너지 감쇄가 비교적 적은 surging 형태의 쇄파로 인해 파고 감소는 미미한 것으로 모의 되었다.
Fig. 3.Variation of JONSWAP spectrum as peak enhancement parameter γ varies and spectrum partition for the generation of random waves of varying γ. 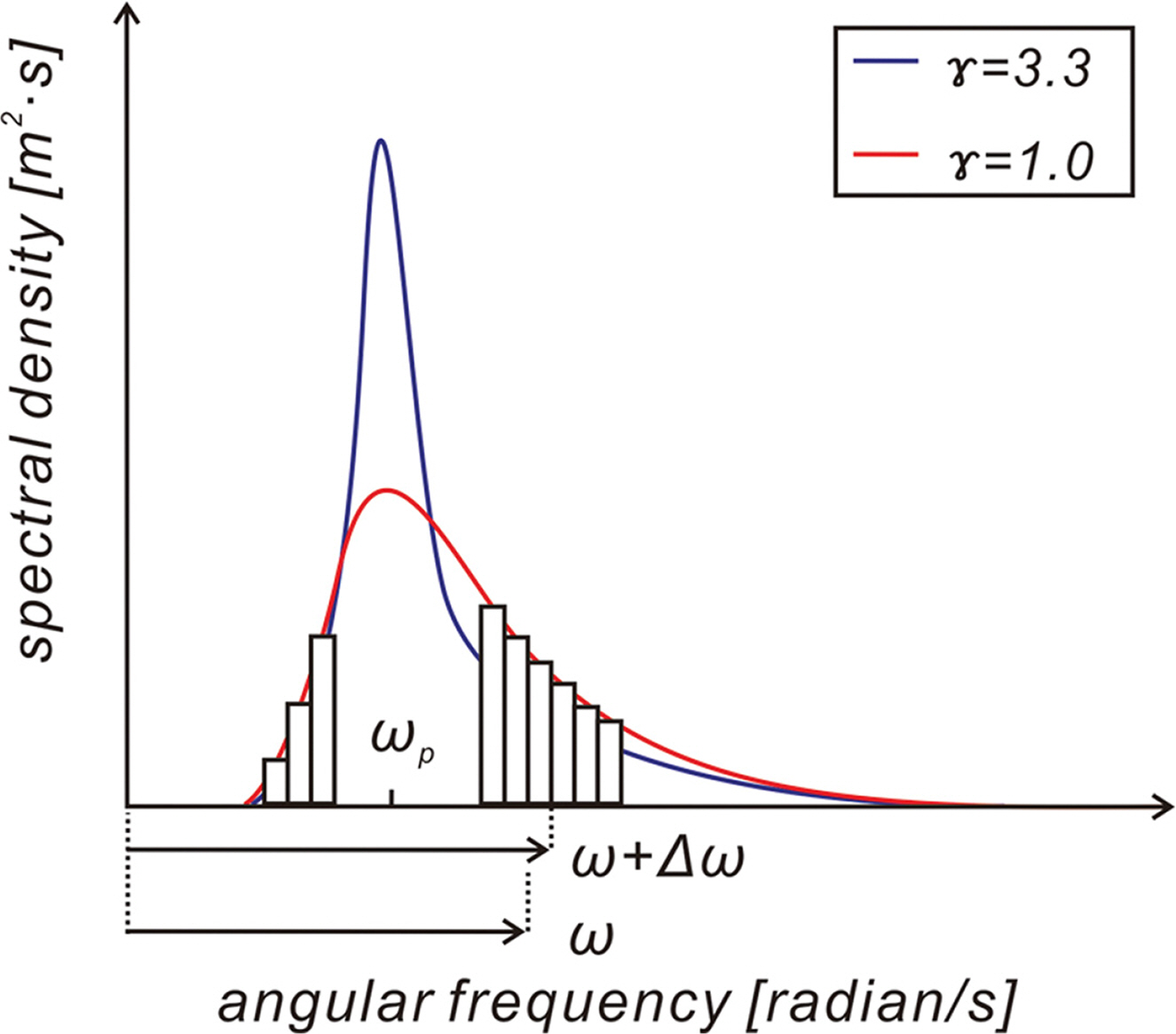
Fig. 4.Snapshots of numerically simulated random waves shoaling toward the beach having a sand bar at its fore-shore. 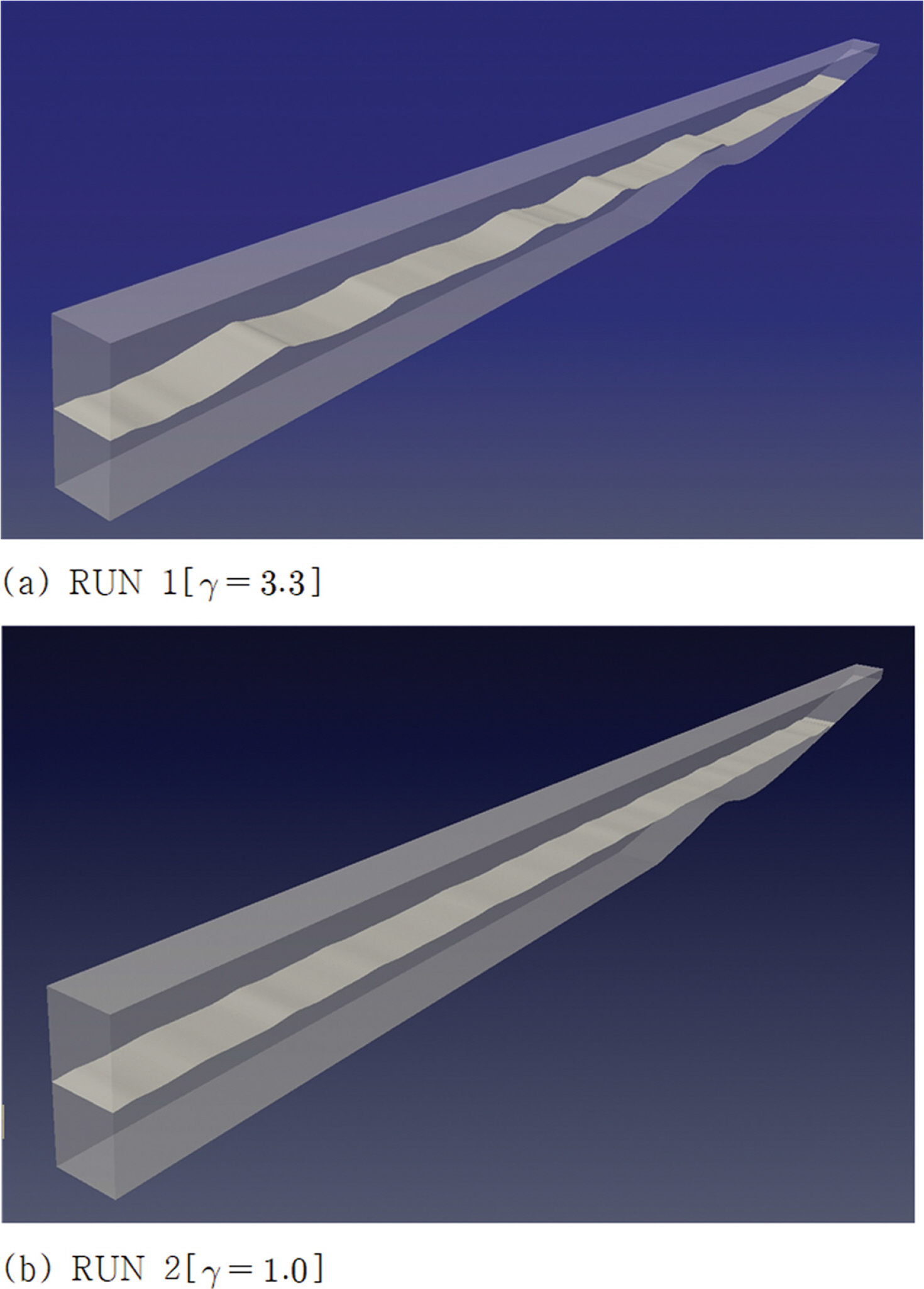
Fig. 5.Sampled time series of numerically simulated random waves measured at Gauge 1, 2, 3, 4 and 5 in RUN 1 and RUN 2. 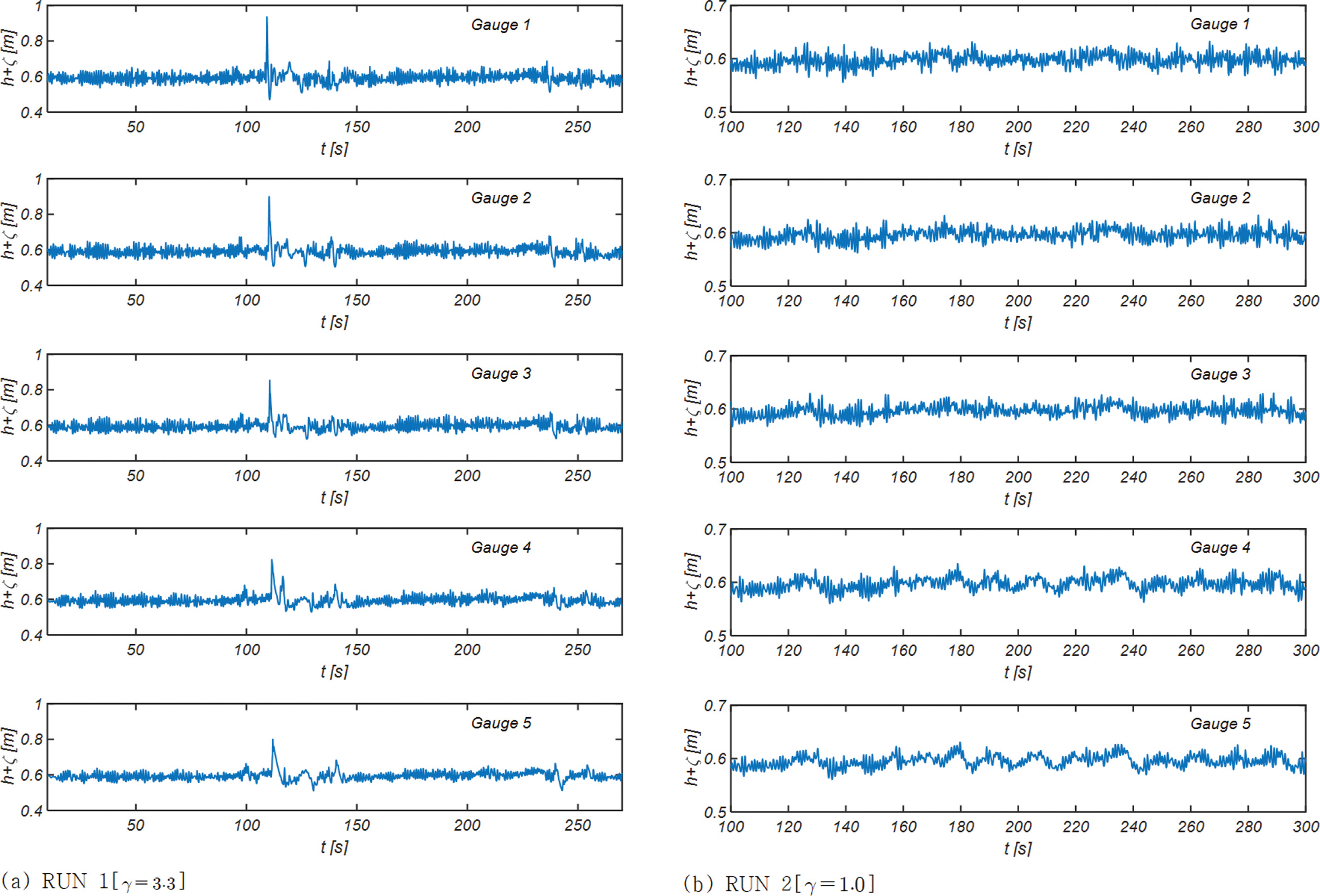
Fig. 6.Evolution of velocity vector from t = 296.8 s to t = 300.1 s at varying heights [Gauge NO 3 in RUN 1]. 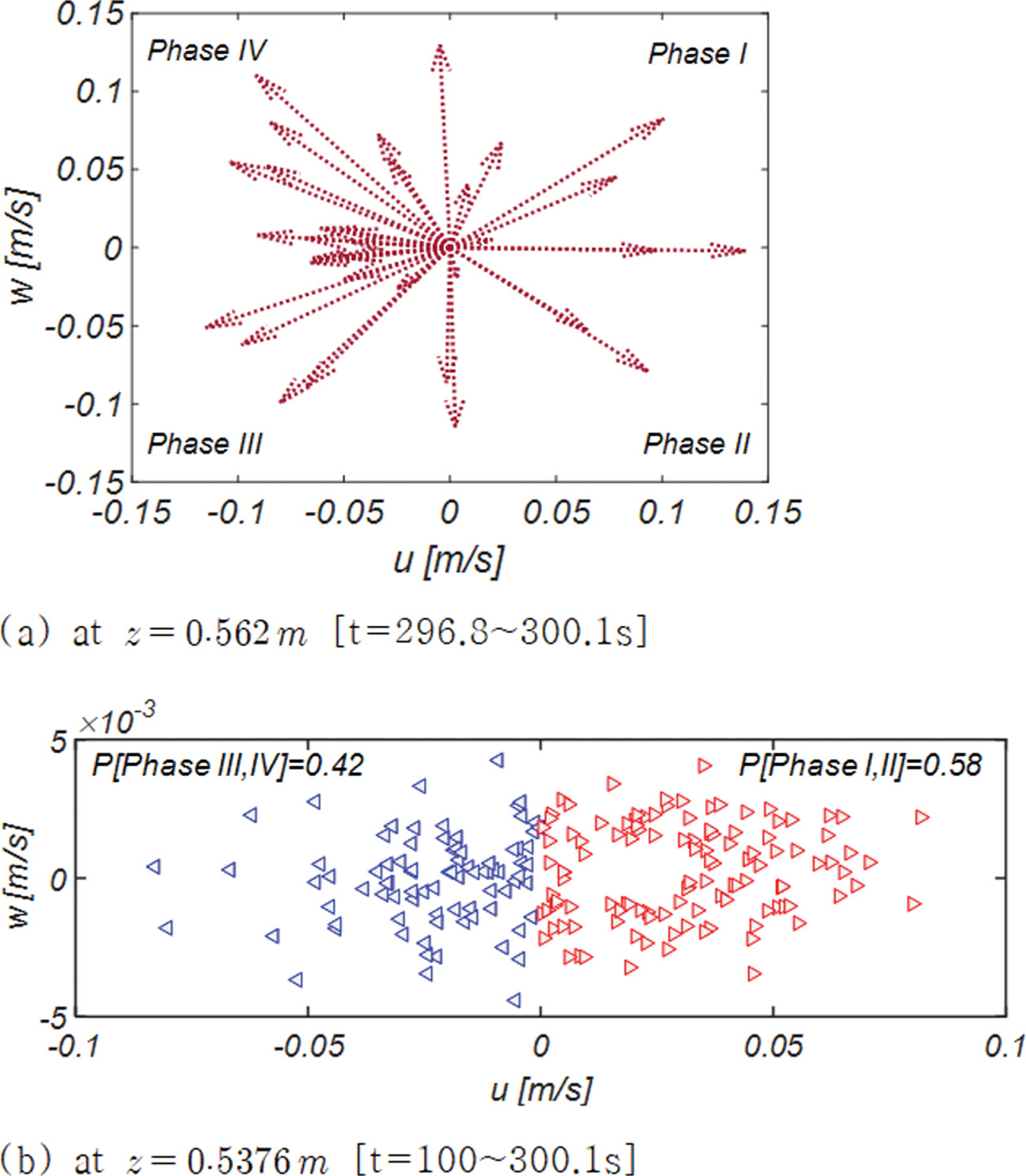
Fig. 7.Sequential snapshots of numerically simulated wave field and its associated stream lines at varying stages of shoaling [in RUN 1]. 
Fig. 8.Sequential vector plots of numerically simulated wave velocity field at varying stages of shoaling [in RUN 2]. 
Fig. 9.Evolution of wave spectra across the shore when random waves are shoaling toward the shore having a sand bar at its fore-shore. 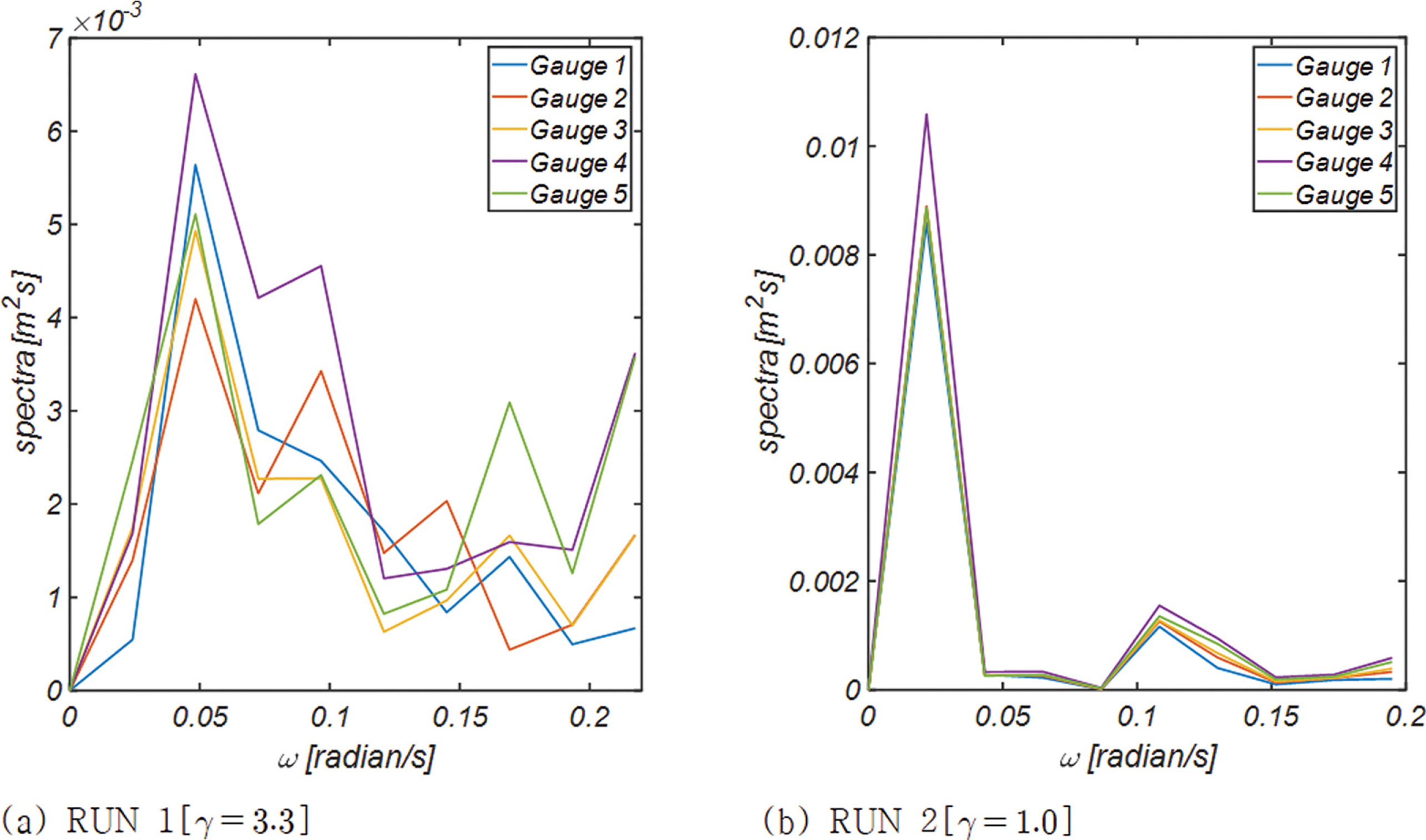
Fig. 11.Sampled wave envelope process estimated by the cubic spline method using the wave crests and troughs detected by Wave-Wave Analysis. 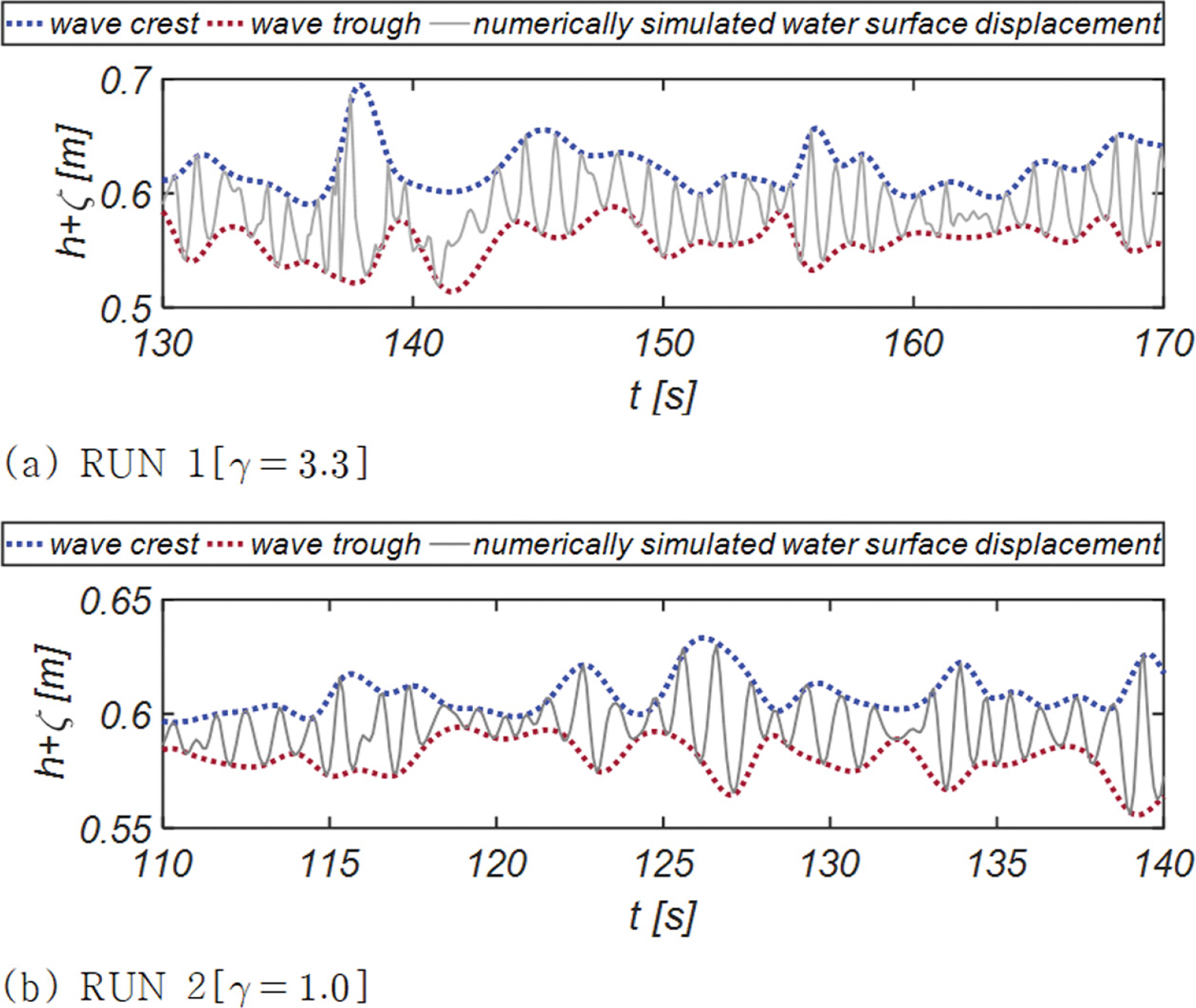
Fig. 13.Comparison of Modified Glukhovskiy wave height distribution and the one derived in this study using the least square method for varying γ. 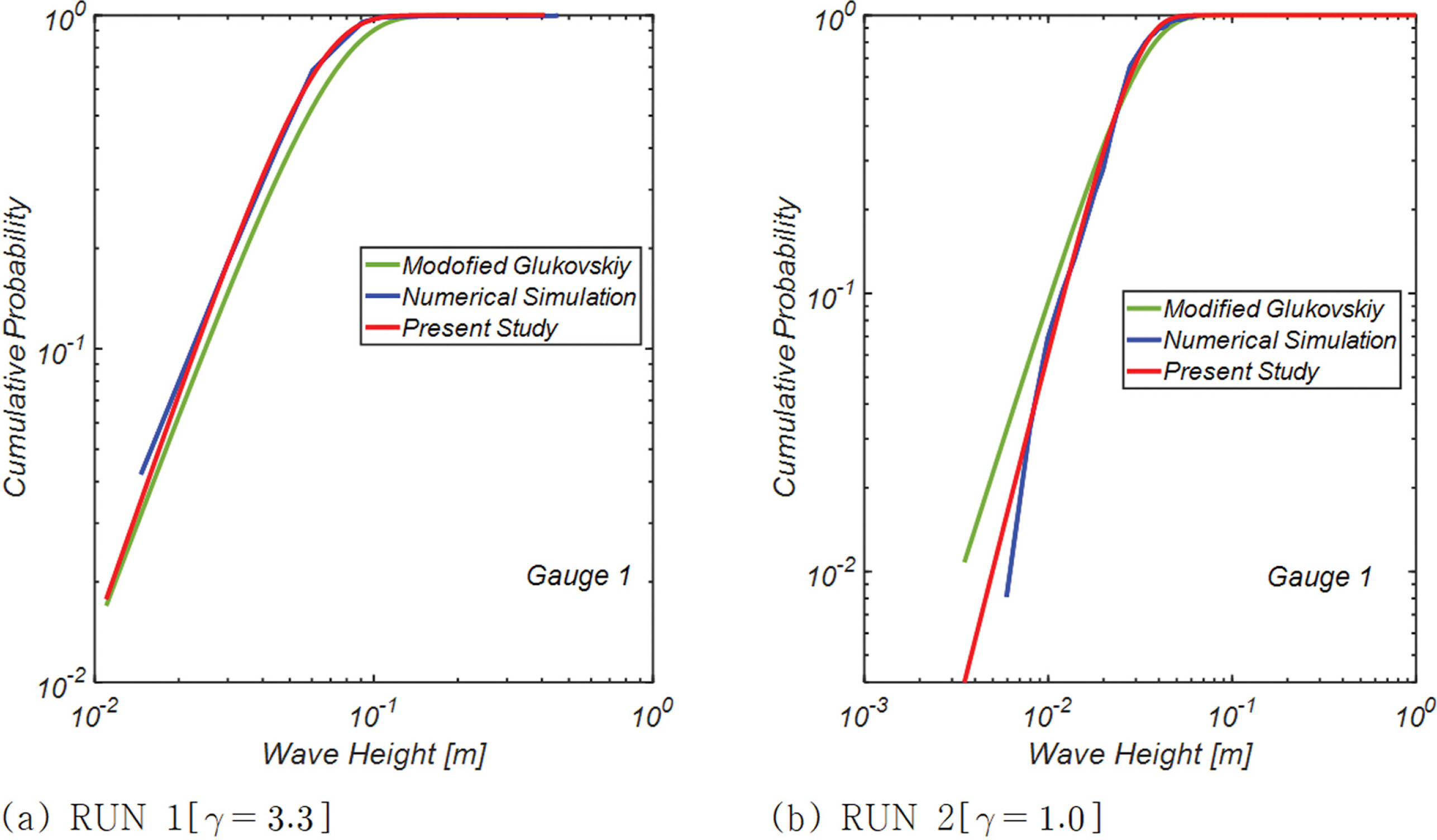
Fig. 14.Comparison of Modified Glukhovskiy wave height distribution and the one derived in this study using the least square method at the varying stages of shoaling process for γ =3.3. 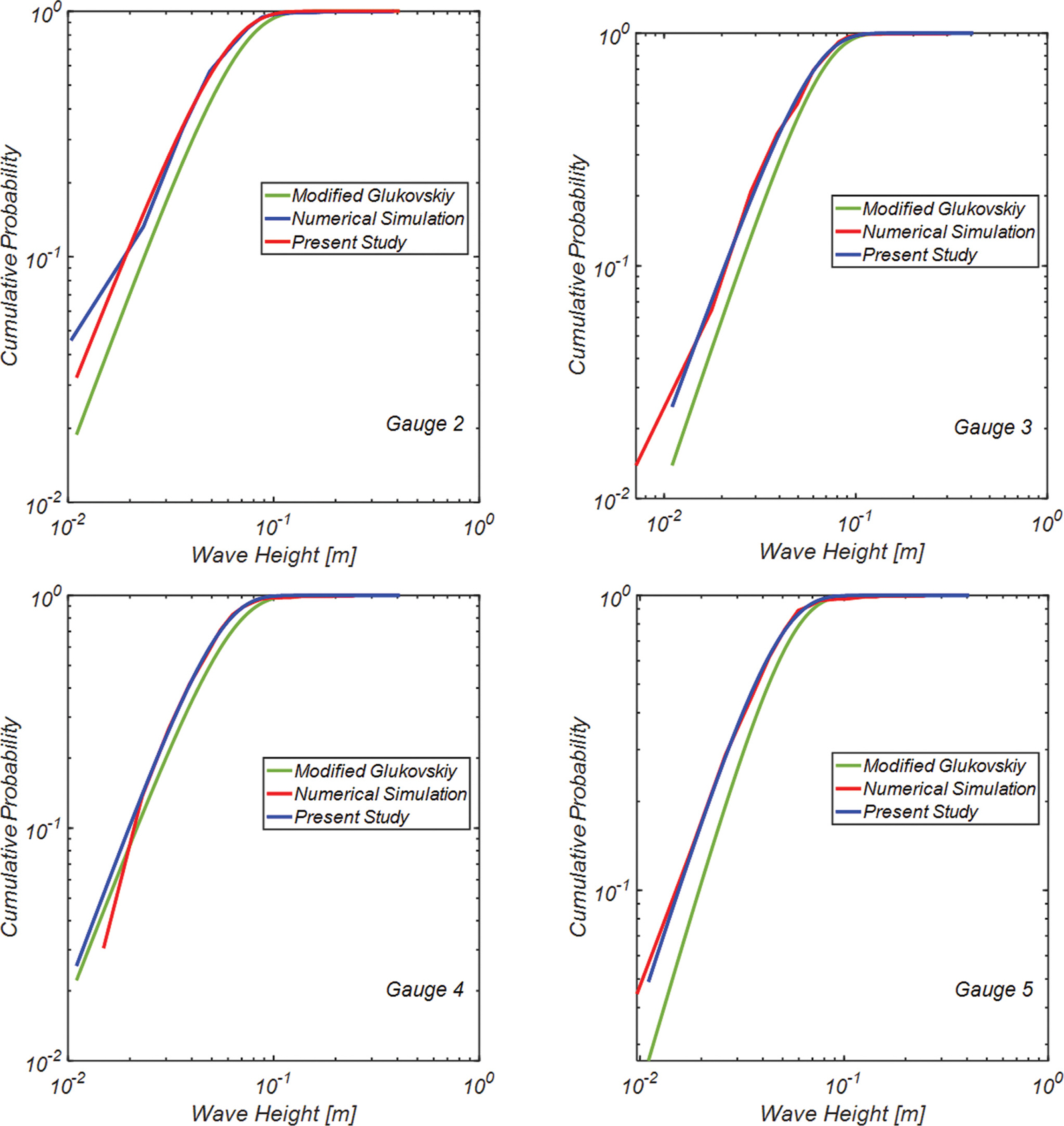
Fig. 15.Evolution of joint distribution of wave height and its associated period as shoaling process goes on in RUN 2 [γ =1.0]. 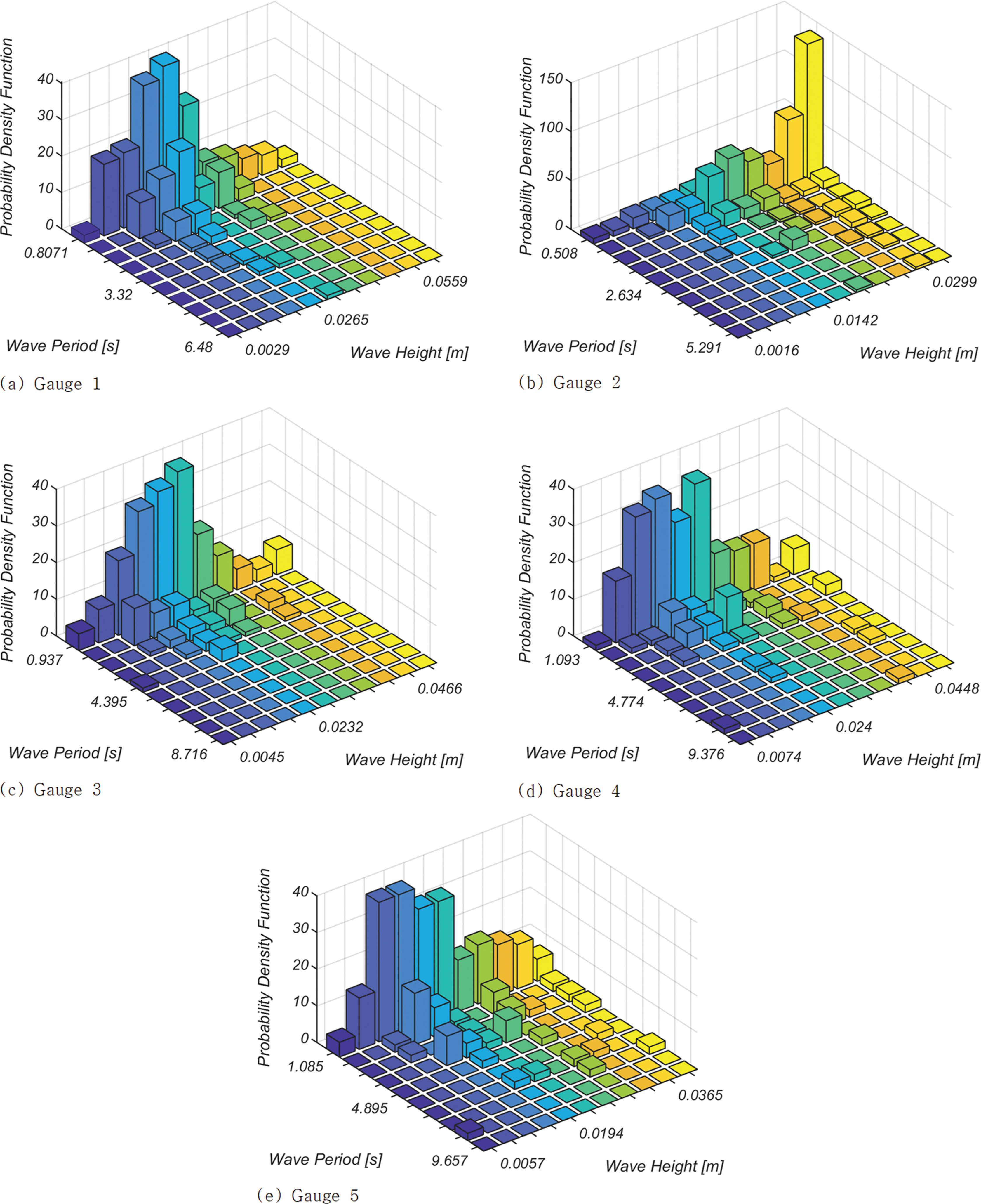
Fig. 16.Evolution of joint distribution of wave height and its associated period as shoaling process goes on in RUN 1 [γ =3.3]. 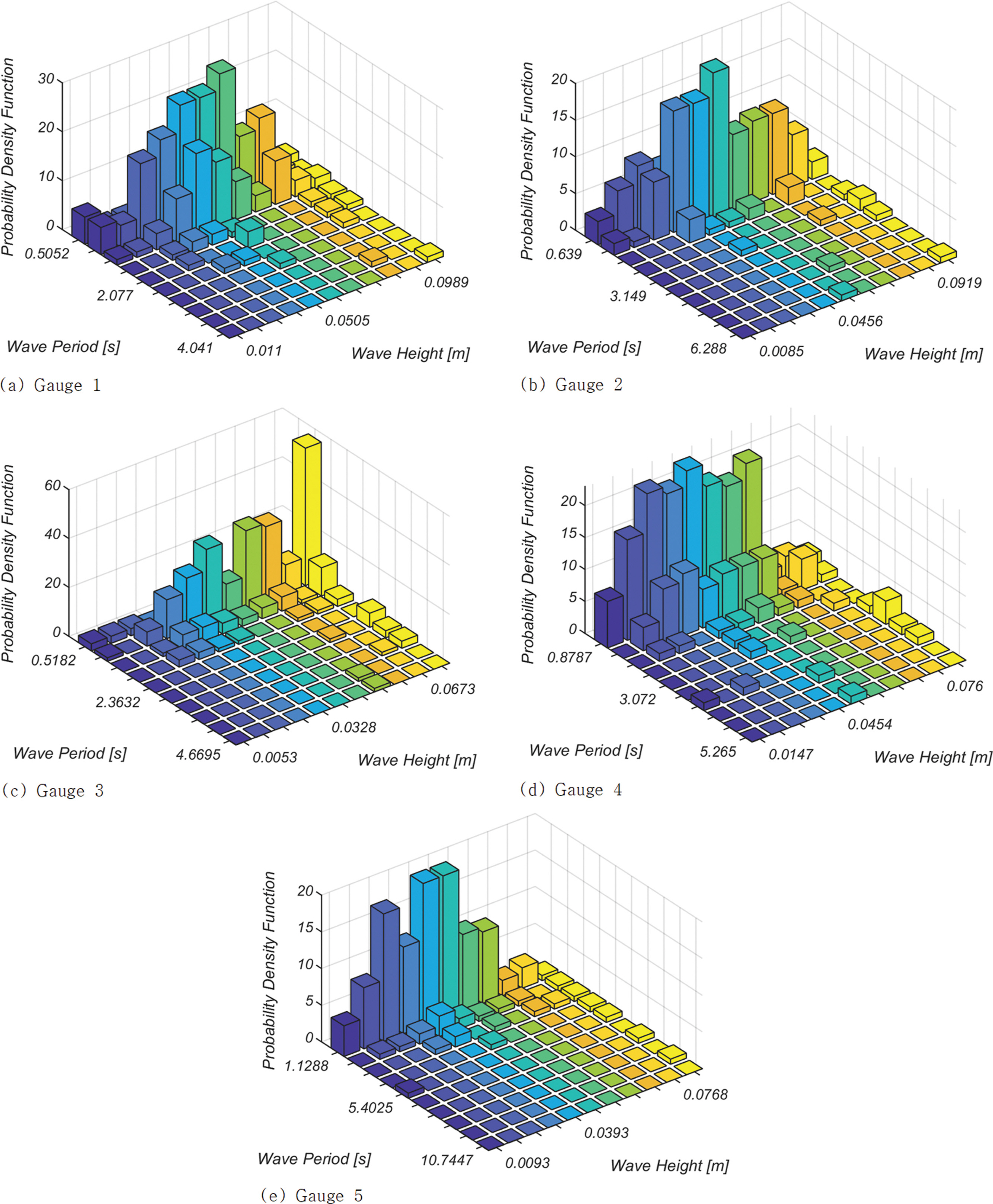
ReferencesBattjes, JA (1986). Energy dissipation in breaking solitary and periodic waves, Delft Univ. of Technology, Communications on Hydraulic and Geotechnical Engineering, No. 1986-5.
Battjes, JA, Groenendijk, HW (2000). Wave height distributions on shallow fore-shores, Coastal Engineering, 40, 161-182.
Chang, PS, Cho, YJ (2019). Preliminary study on the development of a platform for the optimization of beach stabilization measures against beach erosion III - centering on the effects of random Waves occurring during the unit observation period, and infra-gravity waves of bound mode, and boundary layer streaming on the sediment transport, Journal of Korean Society of Coastal and Ocean Engineers, 31(6):434-449.
Cho, YJ (2020a). Numerical analysis of the hydraulic characteristics of a boundary layer streaming over beach cusps surf-zone using LES and one equation dynamic smagorinsky turbulence model, Journal of Korean Society of Coastal and Ocean Engineers, 32(1):55-68.
Cho, YJ (2020b). Numerical analysis of the hydraulic characteristics of a boundary layer streaming over surf-zone using LES and dynamic smagorinsky turbulence model, Journal of Korean Society of Coastal and Ocean Engineers, 32(1):69-84.
Cho, YJ, Kim, IH (2019). Preliminary study on the development of platform for the selection of an optimal beach stabilization measures against the beach erosion-centering on the yearly sediment budget of the Mang-Bang beach, Journal of Korean Society of Coastal and Ocean Engineers, 31(1):28-39.
Cho, YJ, Kim, IH, Cho, YJ (2019). Numerical analysis of the grand circulation process of Mang-Bang beach-centered on the shoreline change from 2017.4.26 to 2018.4.20, Journal of Korean Society of Coastal and Ocean Engineers, 31(3):101-114.
Choi, SH, Cho, YJ (2019). Development of a probabilistic model for the estimation of yearly workable wave condition period for offshore operations-centering on the sea off the ulsan harbor, Journal of Korean Society of Coastal and Ocean Engineers, 31(3):115-128.
Frigaard, P, Anderson, TL (2010). Technical Background Material for the Wave Generation Software AwaSys 5, DCE Technical Reports No. 64, Aalborg University.
Glukhovskiy, BKh (1966). Investigation of sea wind waves (in Russian), Leningrad, Proc. of Sea Climatology Conference, 51-71.
Hasselmann, K (1967). A criterion for nonlinear wave stability, Journal of Fluid Mechanics, 30(4):737-739.
Jeong, WM, Oh, SH, Ryu, KH, Back, JD, Choi, IH (2018). Establishment of Wave Information Network of Korea (WINK), Journal of Korean Society of Coastal and Ocean Engineers, 30(6):326-336.
Kim, SW, Suh, KD, Oh, YM (2005). Comparative study of reliability design methods by application to Donghae Harbor breakwaters. 1. Stability of amor blocks, Journal of Korean Society of Coastal and Ocean Engineers, 17(3):188-201.
Kim, SW, Suh, KD, Lee, CE, Park, DH (2009). Reliability analyses of breakwater armor blocks of harbors in Korea, Journal of Korean Society of Coastal and Ocean Engineers, 21(1):15-29.
Klopman, G. (1996). Extreme wave heights in shallow water, H2486, Delft Hydraulics. The Netherlands.
Klopman, G, Stive, MJF. (1989). Extreme waves and wave loading in shallow water, paper presented at the E&P Forum Workshop in Paris, Delft Hydraulics. The Netherlands.
Longuet-Higgins, MS (1952). On the statistical distributions of heights of sea waves, J. of Mar. Res, 11, 245-266.
Ochi, MK. (1992). Applied Probability & Stochastic Processes, in Engineering & Physical Sciences. John Wiley & Sons.
Park, SH, Cho, YJ (2019). The joint distribution of wave height and its associated period in nonlinear random waves, Journal of Korean Society of Coastal and Ocean Engineers, 31(5):278-293.
Phillips, OM. (1980). The Dynamics of the Upper Ocean. 2nd edition. Cambridge: Cambridge University Press.
PIANC. (1992). Analysis of rubble mound breakwaters, Report of working group 12 of PTC II. Supplement to Bulletin 78/79PIANC General Secretariat, Brussels. ISBN 2-87223-047-5..
Smagorinsky, J (1963). General circulation experiments with the primitive equations, Monthly Weather Rev NWB, 91(3):99-164.
Suh, KD, Kweon, HM, Yoon, HD (2003). Calculation of expected damage to breakwater armor blocks considering variability in wave direction, Journal of Korean Society of Coastal and Ocean Engineers, 15(1):21-32.
van Vledder, GP, Ruessink, G, Rijnsdorp, DP. (2013. Individual wave height distributions in the coastal zone: Measurements and simulations and the effect of directional spreading, In Coastal Dynamics 2013: 7th International Conference on Coastal Dynamics. Arcachon, France.
|
|
|||||||||||||||||||||||||||||||||