요약본 연구에서는 CADMAS-SURF 모형을 사용하여 케이슨 직립제의 상부에 패러핏의 설치 위치에 따라서 규칙파에 의한 파압과 파력의 특성을 분석하였고, 파력결과를 사용하여 방파제 및 지반 안정성 평가를 수행하였다. 수치해석결과, 후부 패러핏을 채택하면 전면 최대 파압 및 파력을 저감시킬 수 있으며, 패러핏에 작용하는 최대 파압은 전면에 있는 경우에 비하여 다소 증가하나 전면 최대 파압과의 위상차에 의해 방파제의 안정성에는 거의 영향을 미치지 못함을 확인하였다. 그리고 Yamamoto et al.(2013)이 후부 패러핏의 문제점으로 지적한 바 있는 충격파압은 발생하지 않았다. 활동, 전도에 대한 안정성 검토 결과, 후부 패러핏 구조를 채택하면 항외측에 패러핏을 설치한 경우에 비하여 13% 적은 자중으로도 목표 안전율인 1.2를 확보할 수 있는 것으로 평가되었다. 이때 최대 지반지지력도 30% 감소되는 것으로 확인되어 후부 패러핏 구조의 실제 현장에서의 적용성이 높은 것으로 평가되었다.
AbstractIn this study, using the CADMAS-SURF model, the characteristics of the wave pressures and the wave forces were analyzed according to the installation position of the parapet on top of the caisson, and the stability evaluation was carried out using estimated wave forces for the design wave condition. Numerical results show that adopting the rear-parapet reduces the front maximum wave pressures and wave forces, and the maximum wave pressure acting on the rear-parapet increases slightly compared to the front parapet, but the wave force acting on the rear-parapet has little effect on the stability of the breakwater due to the phase difference with the wave force acting on the front of the breakwater. In addition, impulsive wave pressures did not occur, as Yamamoto et al. (2013) pointed out the problem of the rear-parapet breakwater. As a result of the stability against sliding and overturning, it was estimated that the target safety factor of 1.2 could be secured by the self-weight of 13% less than the case of the front parapet. At this time, the maximum ground pressure was also reduced by 30%, and the applicability of the rear-parapet structure to the actual site was evaluated as high.
1. 서 론지구온난화에 의하여 해수면상승은 물론이고 해수온도가 상승하여 태풍의 강도도 증가하고 있는 추세이다(Yamada et al., 2017; IPCC, 2019). 이로 인하여 대형 태풍에 의해 설계 파고를 상회하는 이상파랑이 발생하여 보강된 항만구조물이 다시 피해를 입고 있는 것이 현실이다(Hyein E&C, 2012; DY Engineering, 2013; SEKWANG EnC, 2018). 이러한 환경적인 변화에서 항만을 안전하게 지키기 위해서는 우선적으로 외해로부터 진입하는 파랑을 최전방에서 막는 방파제의 안정성을 확보해야만 한다.
설계파고의 증가는 항내 정온도 및 항내 시설의 안전을 위해 상치콘크리트 패러핏 높이의 증대를 요구한다. 이는 결국 방파제에 작용하는 파력을 증가시키며, 방파제의 안정성을 확보하기 위한 자중의 증대로 이어진다. 자중의 증가는 사석마운드의 지지력과 케이슨의 바닥판의 안전과 연관되어 종합적인 고려가 필요하다. 그래서 최근 국내에서는 케이슨 방파제의 보강설계시 패러핏은 설계기준에 따라 높이고, 케이슨에 작용하는 최대 파력을 용이하게 줄일 수 있는 방파제 전면을 소파블록으로 피복하는 방법을 많이 채택하고 있다(Cho et al., 2018; Hong et al., 2018). 기존 케이슨에 새로운 케이슨을 추가로 설치하여 보강하는 방안도 채택되고 있는데(Ko et al., 2011; SEKWANG EnC, 2018), 이 경우는 신·구 케이슨을 일체화시키는 것이 불가능하여 설계시 이를 어떻게 고려해야 할지에 대해 고심하고 있는 것이 현실이다.
패러핏은 효율적으로 월파를 차단하기 위해 상치 콘크리트의 항외측에 두는 것이 일반적이다. 상치콘크리트의 무게 중심이 방파제 중심에서 항외측으로 가도록 하는 것이 기초사석마운드 지지력측면에서 다소 유리하다는 것이 또 다른 이유이기도 하지만 다분히 항만 설계업계의 관행인 것으로 판단된다. 패러핏을 항내측에 위치시키면, 방파제 표면에 작용하는 동수압의 위상차에 의하여 방파제의 안정성과 기초마운드 지지력 측면에서 크게 도움이 된다. Yamamoto et al.(2013)의 선행연구에서 월파량이 증대되고, 패러핏에 충격파압이 작용될 수 있다고 제시되기는 했지만 패러핏을 항내측에 두는 것이 경제적이기 때문에 관심을 가져볼 만하다. 패러핏을 Flare, Bullnose 등의 반파공으로 설계한다면 월파량 증대에 효율적으로 대응할 수 있고(Oh, 2016; Jung and Yoon, 2019) 충격성 파압 발생을 억제시킬 수 있어, 패러핏 위치에 대한 고정관념의 변화와 설계파고 증가에 따른 방파제의 패러핏 높이 증대 등 보강설계에 활용이 기대된다.
본 연구에서는 기존 케이슨 방파제의 보강시와 신설 방파제 설계시 패러핏의 위치를 효율적으로 배치하는데 도움을 주기 위하여 패러핏의 위치가 방파제의 안정성에 미치는 영향에 대해서 살펴보았다. CADMAS-SURF(CDIT, 2001)를 사용하여 케이슨식 직립제를 대상으로 패러핏의 위치 변화에 따른 규칙파에 대한 수치해석을 실시하여, 파고와 주기의 변화에 따른 파압 및 위상차를 분석하였고, 충격적인 파압의 발생유무를 검토하였으며, 그리고 방파제에 작용하는 총 파력의 특성에 대해서도 분석하였다. 또한, 설계파 조건을 설정하여 활동, 전도, 지반지지력에 대한 안정성에 검토를 수행하였고, 상대적으로 패러핏의 위치 변화에 따른 파력감소효과가 안정성에 미치는 영향을 분석하였다.
2. 수치해석2.1 수치모형 및 해석 제원본 연구에서는 패러핏의 설치 위치에 따라서 케이슨(패러핏을 제외한 상치콘크리트 포함)과 패러핏 전면에 작용하는 파압을 해석하기 위하여 CADMAS-SURF(CDIT, 2001)를 이용하였다. 이 수치모형은 2차원 비압축성 점성유체를 대상으로 하는 연속방정식과 Navier-Stokes 방정식을 Porous 모형(Sha et al., 1978)에 근거하여 확장한 식을 기본으로 하고, 구조물의 형상근사정도를 높인 것이다(Sakakiyama et al., 1990). VOF(Volume Of Fluid) 방법을 사용하여 자유수면을 추적하고(Hirt and Nichols, 1981), 경계면에 Sommerfeld 방사경계와 에너지 감쇠대를 적용하여 구조물에서 발생하는 반사파를 흡수할 수 있도록 구성되어 있다. 또한, 계산영역 내부에서 파랑을 조파할 수 있으며, 경계면에서의 조파도 가능하다.
본 수치해석에는 k-ε 방정식을 적용하여 난류해석을 수행하였고, 입사파 조건이 비선형성이 강해 경계면에서 stream 22(Dean, 1965) 함수를 사용하여 조파하였다.
Fig. 1에 본 연구에서 대상으로 한 케이슨식 직립제의 개념도를 제시하였다. 해석의 편의상 기초사석마운드는 없는 것을 대상으로 하였으며, 패러핏의 위치에 따른 위상차 효과를 살펴보기 위하여 패러핏의 위치를 세 가지 다른 경우(lp = 0, 20, 40 cm)를 고려하였다. 그리고 파고(H)와 주기(T)의 영향을 알아보기 위하여 주기가 2.0초일 때 파고는 10, 15 cm, 주기가 1.5초일 때 파고 10 cm 인 세 가지 규칙파 조건 대하여 수치해석을 수행하였으며, 설계파는 주기 2.0초이고 파고 15 cm인 조건으로 가정하였다. 이 수치실험 조건은 수리실험과의 비교를 위하여 수조제원을 감안하여 설정한 것으로, 축척은 1/40을 가정하였다.
Fig. 2는 수치해석을 수행한 계산영역의 예를 도시한 것으로 패러핏의 위치가 40 cm인 경우이다. 수심(h)은 45 cm, 천단고(hc)는 25 cm로 고정하였고, 전벽 천단고(hc')는 5 cm로 고정하였다. x축 방향으로의 길이는 2,050 cm로 주기 2.0초에 대한 파장(L)을 기준으로 하여 구조물로부터 약 5파장 떨어지도록 설정하였으며, z축 방향으로의 길이는 80 cm로 모든 해석에 동일하게 적용하였다. 격자크기는 ∆x = 1 cm, ∆z = 0.5 cm의 등간격자로 하였고, 해석시간은 50초로 설정하고, 조파경계에서 발생하는 재반사파가 구조물에 도달하기 전까지의 결과를 분석하였다.
2.2 파압 및 수면변위 측정케이슨, 상치콘크리트, 패러핏의 전면에 작용하는 파압을 측정하여 파력을 계산하고 안정성 검토를 수행하기 위하여 패러핏의 위치가 항외측인 경우(Model 1, lp = 0 cm), 중간인 경우(Model 2, lp = 20 cm), 항내측인 경우(Model 3, lp = 40 cm)에 대하여 각각 18개의 위치에서 파압(p1~p18)을 측정하였다(Fig. 3 참조). 파압 p1부터 p18까지의 측정 위치는 바닥으로부터 0.25, 3.25, 7.75, 12.75, 17.75, 24.75, 30.25, 35.75, 41.25, 44.75, 46.75, 49.75, 50.25, 52.25, 57.25, 61.75, 64.75, 69.75 cm이다. 파압분석 및 파력특성 분석시 참고하기 위하여 케이슨과 패러핏의 전면에서의 수면변위를 측정하였다.
3. 수치해석 결과 분석3.1 동수압 특성
Fig. 4는 설계파 조건일 때(H = 15 cm, T = 2.0초) Model3에 대한 해석결과를 도시한 것으로, 특정 시간대의 전압력 및 수면변위의 변화를 볼 수 있다. ηc, max는 정수면을 기준으로 케이슨 전면에서의 최대 처오름 높이이고, ηp, max는 케이슨 상부를 기준으로 패러핏 전면에서의 최대 처오름 높이이다. 입사파가 케이슨 상부로 월파하게 되고, t = 19.7초 근처에서 케이슨 처오름 높이가 최대가 된다(ηc, max). 월파한 수괴가 케이슨 상부면을 따라 이동하다가 패러핏에 부딪혀 처오르게 되고, t = 20.1초에서 패러핏의 처오름 높이는 최대가 된다(ηp, max). 이 경우, 케이슨 전면과 패러핏에서의 최대 처오름 높이가 발생하는 시점이 주기의 20%에 해당하는 시차(0.4초)가 발생함을 알 수 있다. 또한, 케이슨 전면에 최대 처오름 높이가 발생할 때 패러핏에는 거의 월파한 수괴가 도달하지 않고 있고, 패러핏에 최대 처오름 높이가 발생될 때는 케이슨 전면에 처오름 높이는 낮아지는 것을 알 수 있다.
Fig. 5~7은 케이슨 전면 정수면(pc = p10)과 패러핏 하단(pp= p13)에서의 파압과 케이슨(ηc) 및 패러핏(ηp) 전면에서의 처오름 높이에 대한 시계열을 도시한 것이다. 그림을 살펴보면, 패러핏 위치가 내측으로 갈수록 최대 파압간 위상차가 더 크게 나타나며, 패러핏을 내측으로 이동시키면 케이슨 전면 정수면에서의 최대 파압이 감소하며, 패러핏 하단에 작용하는 최대파압은 패러핏 위치와 작용파의 주기와 파고에 따라 증감이 있음을 알 수 있다. 그리고 같은 주기에 파고가 다른 Fig. 5와 6을 비교하면, 월파한 수괴가 패러핏에 도달하는 시간이 주기뿐만 아니라 파고와도 관계있음을 알 수 있다.
Fig. 5에서 Model 2의 패러핏 하단에 작용하는 파압이 쌍봉형태의 첨두치를 보임을 알 수 있다. 이러한 쌍봉형은 Bernoulli 식으로부터 이해할 수 있다. 즉, Bernoulli 식을 이용하면 동수압은 식(1)로 표현된다. 여기서, 편의상 선형파 이론에 의한 해를 이용하면 진행파의 속도포텐셜은 식(2), 식(1)의 미분항은 식(3), 식(1)의 수직성분 수입자속도는 식(4)와 같다. Fig. 4에서와 같이 월파한 수괴가 패러핏에 도달하면 처올림 높이가 상당히 커지게 되므로 패러핏 전면의 수직성분 수입자속도는 상당히 빠를 것이다. 식(4)의 수직성분 수입자 속도는 식(1)에서 사인함수의 제곱으로 표현되며, 식(3)의 속도포텐셜의 시간에 대한 미분항은 코사인 함수로 표현된다. 90도의 위상차를 가지는 두 성분의 합성에 의해 결정되는 압력은 속도포텐셜의 시간에 대한 미분항에 비하여 수직성분 수입자속도의 영향이 작으면 압력은 하나의 봉우리로 나타나게 되고, 수직성분 수입자속도의 영향이 크면 압력은 쌍봉형태가 된다. 즉, 패러핏 전면의 하단에 작용하는 압력은 속도포텐셜의 시간에 대한 미분항에 비하여 수직성분 수입자속도의 영향이 커서 쌍봉형태로 나타나게 된 것으로 보인다.
이러한 결과를 보다 정량적으로 살펴보기 위하여, Fig. 8에 케이슨 전면 정수면과 패러핏 하단에서의 평균최대파압을 패러핏의 입사파장(L)에 대한 상대위치(lp/L)에 따라서 도시하였다. 평균최대파압은 Fig. 5~7에서 보여주는 시간 범위내의 1주기당 최대파압(5개)을 평균한 것이다. 그림을 보면 무차원 파압이 실험한 모든 조건에서 1.0보다 작음을 알 수 있는데, 이는 Yamamoto et al.(2013)이 수리실험을 통하여 보고한 후부 패러핏에서의 충격 파압 발생과는 다른 결과이다. Yamamoto et al.의 실험에서는 소파블록으로 피복된케이슨 방파제를 대상으로 했다는 점과 불규칙파를 사용했다는 점을 고려해 보면 충분히 발생할 수 있는 현상으로 이해된다.
또한, 전체적으로 패러핏의 위치가 중간이나 항내측으로 설치되는 경우의 케이슨 전면 정수면에서의 평균최대파압(
패러핏 하단에서의 평균최대파압(
앞의 Fig. 5~7에서 언급한 바와 같이 패러핏을 항내측으로 위치시킬 경우, 방파제 전면에 작용하는 최대파압과 패러핏에 작용하는 최대파압은 상당한 위상차를 보이게 된다. 이 위상차는 방파제의 안정성에 있어서 중요하다. 즉, 방파제 안정성 평가시 패러핏에 작용하는 파력을 어느 정도 고려할지를 판단하는데 중요한 정보가 될 수 있다.
본 연구에서는 이를 추정하기 위한 방안으로 방파제를 월파한 수괴가 천해파의 파속(
3.2 파력 특성
Fig. 3의 18개 위치에서의 파압으로부터 파력을 계산하여 작용파 조건에 따라 Fig. 10~12에 제시하였다. 패러핏 위치가 방파제의 안정성에 미치는 영향을 정량적으로 평가하기 위하여, 방파제 전면에 작용하는 파력(Fc)과 패러핏에 작용하는 파력(Fp), 그리고 이 두 힘을 합한 방파제에 작용하는 총파력(FT)을 구분하였다. 편의상 계산된 파력은 패러핏이 항외측에 위치한 Model 1의 최대파력(FT, s)으로 무차원화하였다.
그림을 살펴보면 패러핏을 항내측으로 위치시키면(Model 2와 3) 방파제 전면 파력이 감소함을 알 수 있으며, 패러핏의 위치(lp)가 항내측으로 이동할수록(Model 1→Model 2 Model 3) 방파제 전면과 패러핏에 작용하는 최대파력 간의 위상차가 커지는 것을 확인할 수 있고, Model 3의 경우는 위상차에 의하여 패러핏에 작용하는 파력이 최대총파력에 거의 영향을 미치지 못함을 알 수 있다. 또한, 패러핏은 방파제 전면 면적의 40%를 차지하지만 패러핏에 작용하는 파력(Fp)는 방파제 전면에 작용하는 파력(Fc)에 비하여 작음을 알 수 있다.
방파제의 안정성에 영향을 미치는 파력특성을 정량적으로 살펴보기 위하여, 패러핏의 상대위치(lp/L)에 따라서 방파제에 작용하는 평균최대총파력(
표를 보면, 입사파 조건과 패러핏 위치에 따라 다소 편차가 있지만, 패러핏이 전면에 위치했을 때의 평균최대총파력(
Fig. 13~15은 Model 1과 Model 3의 특정시간의 파압분포를 도시한 것으로, Model 1은 방파제에 작용하는 총파력이 최대(FT, max)일 때 파압분포이고, Model 3은 케이슨에 작용하는 파력이 최대(Fc, max)일 때와 패러핏에 작용하는 파력이 최대(Fp, max)일 때의 파압분포이다. Fig. 13은 설계파 조건으로 파고 15 cm, 주기 2.0초이고, Fig. 14는 파고 10 cm, 주기 2.0초이고, Fig. 15은 파고 10 cm, 주기 1.5초인 경우이다. 각 그림의 (a)는 정수면에서 파압(정수면에서 0.25 cm 아래의 파압)이 최대가 되며, Fig. 13(a)는 0.92, Fig. 14(a)는 1.00, Fig. 15(a)는 0.88이다. 직립제에 작용하는 파압을 이론해와 실험결과를 분석한 연구에 의하면(Goda and Kakizaki, 1966), 상대수심(h/L, relative water depth)이 깊어지고 파형경사(H/L, wave steepness)가 커질수록 정수면에 작용하는 최대파압은 감소하게 된다. 수치해석결과도 이와 같은 경향을 보이는 것을 알 수 있고, 기존 연구(Goda and Kakizaki, 1966)의 정수면에서 직립제에 작용하는 최대파압을 도시한 그림에 의하면, 본 연구의 입사파 조건에 대한 최대파압은 정량적으로 각각 0.93, 1.1, 0.9로 수치해석결과와 매우 근접함을 알수 있다. 그리고 각 그림의 (b)는 방파제 전면에 작용하는 파력이 최대일 때(방파제에 작용하는 총 파력도 최대임)의 파압분포로 패러핏에 작용하는 파압은 무시할 만큼 작은 것을 볼 수 있다. 그리고 각 그림의 (c)는 패러핏에 작용하는 파력이 최대일 때 파압분포로 방파제 전면에 부압이 작용함을 볼 수 있다.
3.3 패러핏 위치에 따른 방파제의 안정성 평가본 절에서는 설계파 조건(파고 15 cm, 주기 2.0초)에 대하여 패러핏의 위치에 따라서 활동과 전도 안정성 검토를 수행하여 방파제의 유효자중을 계산하고, 이를 활용하여 지반지지력 안정성 검토를 수행하였다(Goda, 2010). 그리고 안정성 검토할 때 방파제 상부구조의 무게중심이 케이슨의 가운데로 위치하도록 설계하였다. 활동과 전도에 대한 안정성 평가식은 각각 식(5)와 식(6)으로 표현된다.
여기서, SF, S는 활동에 대한 안전율, SF, O는 전도에 대한 안전율, μ는 정지마찰계수, We(= W - B)는 부력(B)을 제외한 방파제의 유효자중, U는 직립부 저면에 작용하는 양압력, tw는 케이슨의 후면하단(heel)부터 유효자중 및 부력의 작용점까지의 거리, MU는 케이슨의 후면하단에서 양압력 모멘트, MP는 케이슨의 후면하단에서 방파제에 작용하는 수평파력의 모멘트이다. 활동 및 전도에 대한 안전율은 1.2를 적용하였고, 콘크리트와 사석간의 정지마찰계수로 0.6을 사용하였다. Goda의 파압식에 의하면, 케이슨 저면에 사석마운드가 없고 케이슨 전면이 일정수심이면, 항외측 케이슨 저면에 작용하는 압력(pu)은 케이슨 전면의 최하단부에 작용하는 파압과 같다(Fig. 3의 p1). 그래서 양압력은 항외측 케이슨 저면에 작용하는 압력을 p1으로 하고, 항내측 케이슨 저면에 작용하는 압력을 0인 삼각형 분포로 가정하여 계산하였다. 수평파력 모멘트는 Fig. 3의 각각의 측정구간별 파력과 작용점을 이용하여 계산하였다.
Fig. 16에 활동 및 전도 안정성 평가식으로부터 계산한 유효자중을 도시하였다. y축은 유효자중(We)으로 패러핏이 전면에 위치해 있을 때(lp/L = 0) 계산된 유효자중(We, s)으로 무차원화하였다. 활동 안정성 평가식으로부터 도출된 유효자중을 보면, 패러핏 위치가 중간에 위치한 경우(lp/L = 0.0515)는 패러핏이 전면에 위치한 경우보다 약 9%, 후면에 위치한 경우(lp/L = 0.1030)는 약 13% 유효자중이 감소하였음을 알 수 있으며, 전도에 대한 경우도 유사한 정도의 감소효과를 보임을 알 수 있다.
앞에서 계산된 유효자중을 활용하여 지반지지력 검토를 수행하였다. 지반지지력은 아래 식으로 산정할 수 있다(Goda, 2010).
여기서, ph는 케이슨의 후면하단(heel)에 작용하는 지반지지력, pt는 케이슨의 전면하단(tow)에 작용하는 지반지지력, WB는 방파제의 폭, te(=(Wetw - MU - MP)/(We - U))는 케이슨의 후면하단에서 케이슨의 전면방향으로 지반반력(= We - U)의 편심량이다. 식(7)은 케이슨 하단에 삼각형 분포로 지반지지력이 작용하는 경우로, 케이슨 후면하단에서 3te 떨어진 위치에 지반지지력이 0이 된다(pt = 0). 식(8)은 사다리꼴 분포로 가정하여 유도된 식이다.
패러핏의 위치에 따라서 편심량을 계산해본 결과, 본 연구에서 대상으로 한 Fig. 3의 Model 1, 2, 3 모두 식(7)에 해당하여 이에 따라 케이슨 하단에 지반지지력을 계산하였다. 패러핏이 전면에 위치한 경우 지반지지력은 9.817 kN/m2, 패러핏이 중간에 위치한 경우는 8.476 kN/m2, 패러핏이 후면에 위치한 경우는 6.860 kN/m2으로, 패러핏이 전면에 위치한 경우보다 지반지지력이 중간 및 후면에 위치한 경우가 각각 약 14%와 30% 감소하였다. 이는 축척 1/40을 고려하면, 각각 392.693 kN/m2, 339.041 kN/m2, 274.399 kN/m2로 허용지지력 600 kN/m2보다 작은 수준으로 지반지지력 측면에서만 보면 현재 설정된 케이슨 폭(20 m)을 줄일 수 있는 여지가 충분히 있다고 평가할 수 있다.
4. 결 과본 연구에서는 수치해석을 통하여 패러핏의 설치 위치가 케이슨 방파제에 미치는 영향에 대해서 살펴보았다. 도출된 주요 연구결과를 정리하면 다음과 같다.
1. 후부 패러핏을 적용하면 방파제 전면에 작용하는 최대 파압이 감소하며, 패러핏에 작용하는 파압은 다소 증가할 수 있으나, 전면 최대파압과의 위상차가 커 실제로 방파제 안정성에는 거의 영향을 미치지 못하는 것으로 평가되었다. 또한, Yamamoto et al.(2013)의 연구에서 제시된 충격성 파압은 본 실험에서는 발생하지 않았다.
2. 후부 패러핏 케이슨 방파제에 작용하는 총 파력은 패러핏을 전면에 설치한 경우의 총 파력보다 최대 18.56% 정도 감소하였고, 이때의 패러핏에 작용하는 파력의 기여율은 위상차로 인하여 0.27%로 아주 미미하여 무시할 만 한 것으로 평가되었다.
3. 활동 및 전도에 대한 안정중량을 산정해 본 결과, 후부 패러핏 케이슨 방파제의 유효자중은 패러핏을 전면에 설치한 경우의 유효자중에 비하여 87% 수준이고, 지반지지력의 경우는 후부 패러핏을 채택하면 최대 30% 감소시킬 수 있는 것으로 평가되었다.
4. 후부 패러핏에 작용하는 최대 파압의 위상차와 충격성 파압발생 가능성을 판단하는데 기초자료가 될 것으로 판단되는 방파제를 월파한 수괴의 이동속도에 대한 검토 결과, 중복파고에서 방파제의 전벽 천단고(hc')를 뺀 수심에 대한 천해파의 파속으로 이동하는 것으로 가정하면, 패러핏을 방파제 중간에 둔 이동거리가 짧은 경우는 다소 느리게 예측하나, 항내측에 위치시킨 이동거리가 긴 경우에는 상당히 정확하게 예측하는 것으로 평가되었다.
상기 결과는 규칙파에 대한 수치해석에 의해 도출된 것으로, 후부 패러핏 구조의 실제 현장 적용을 위해서는 불규칙파에 대한 검토, 수리모형실험을 통한 결과의 검증 등 추가 연구가 필요하다.
Fig. 5.Time series of wave pressures (pc = p10 and pp = p13) and water surface elevations in front of the caisson with the cap concrete (ηc) and the parapet (ηp): H = 15 cm, T = 2.0 s. 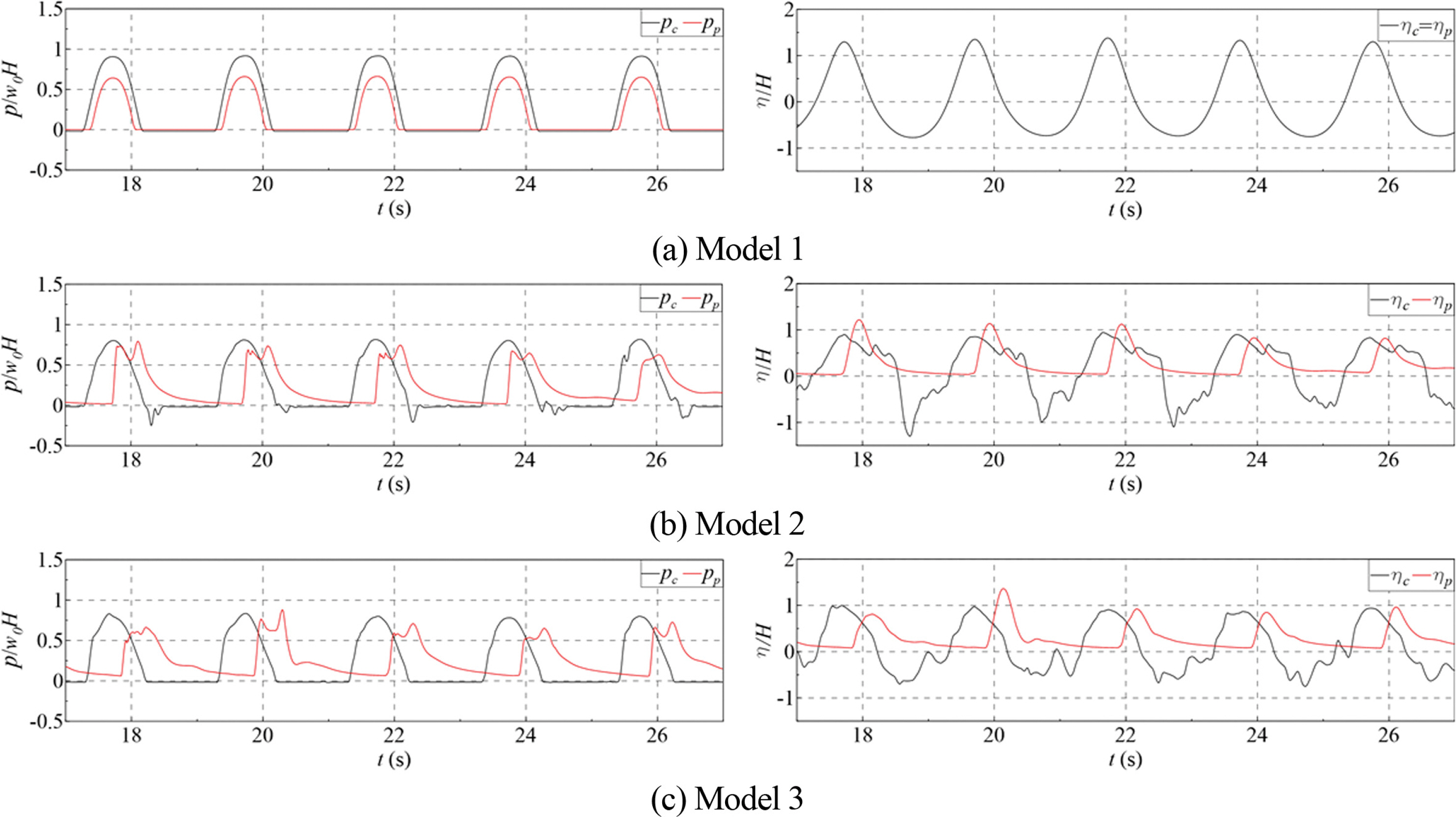
Fig. 6.Time series of wave pressures (pc = p10 and pp = p13) and water surface elevations in front of the caisson with the cap concrete (ηc) and the parapet (ηp): H = 10 cm, T = 2.0 s. 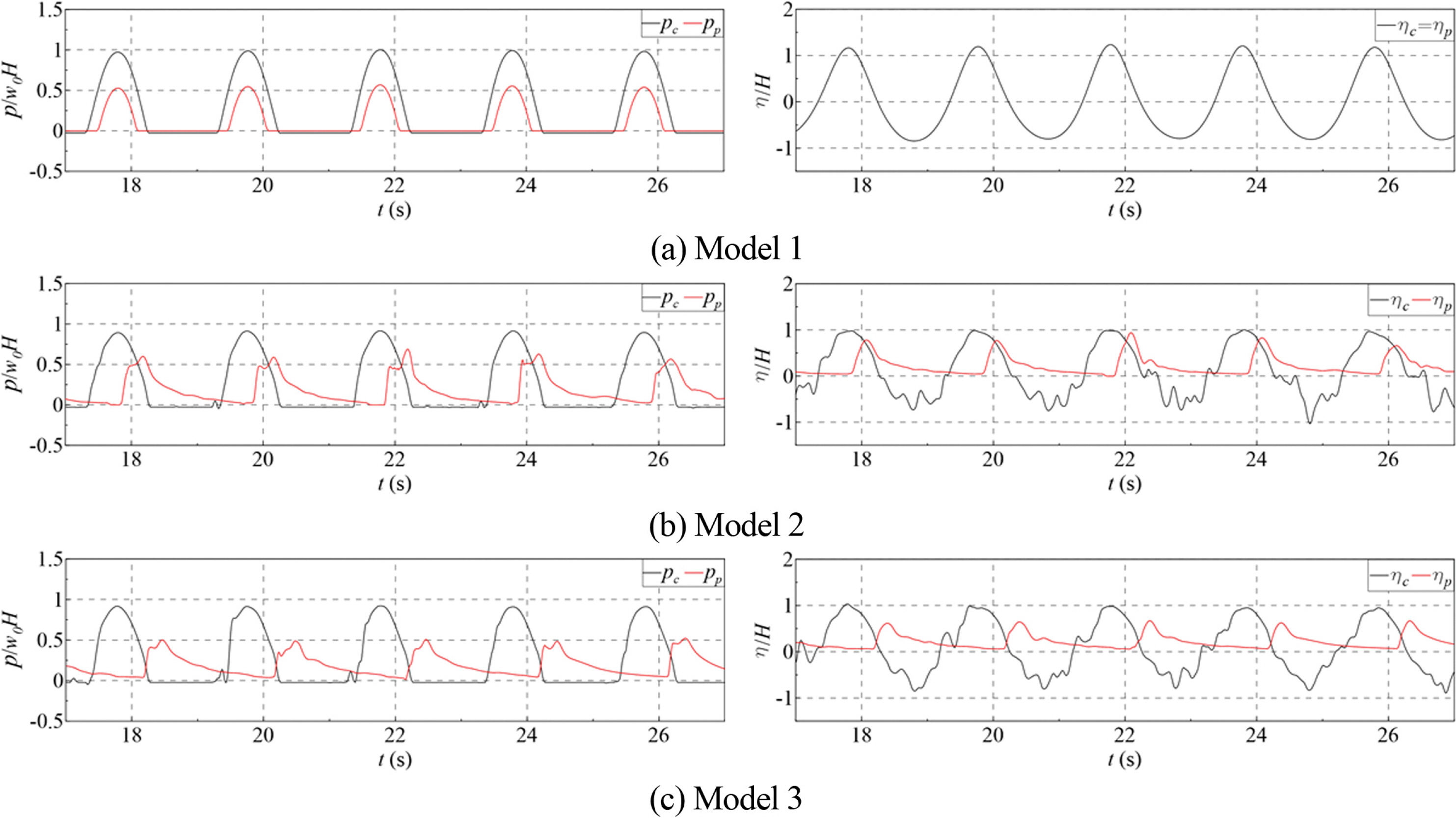
Fig. 7.Time series of wave pressures (pc = p10 and pp = p13) and water surface elevations in front of the caisson with the cap concrete (ηc) and the parapet (ηp): H = 10 cm, T = 1.5 s. 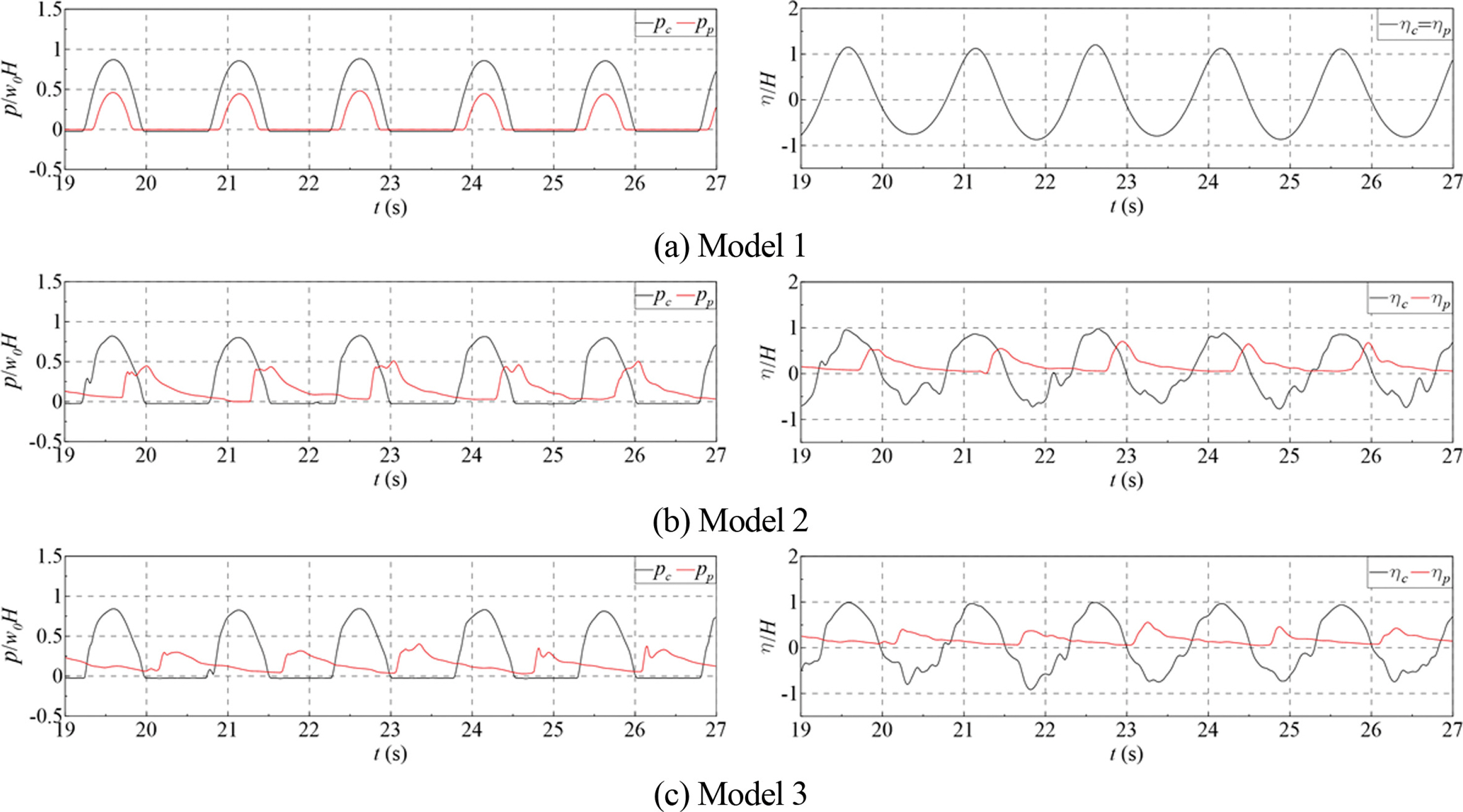
Fig. 9.Phase differences (= 2πt/T) between the maximum wave pressures acting on the caisson and the parapet. 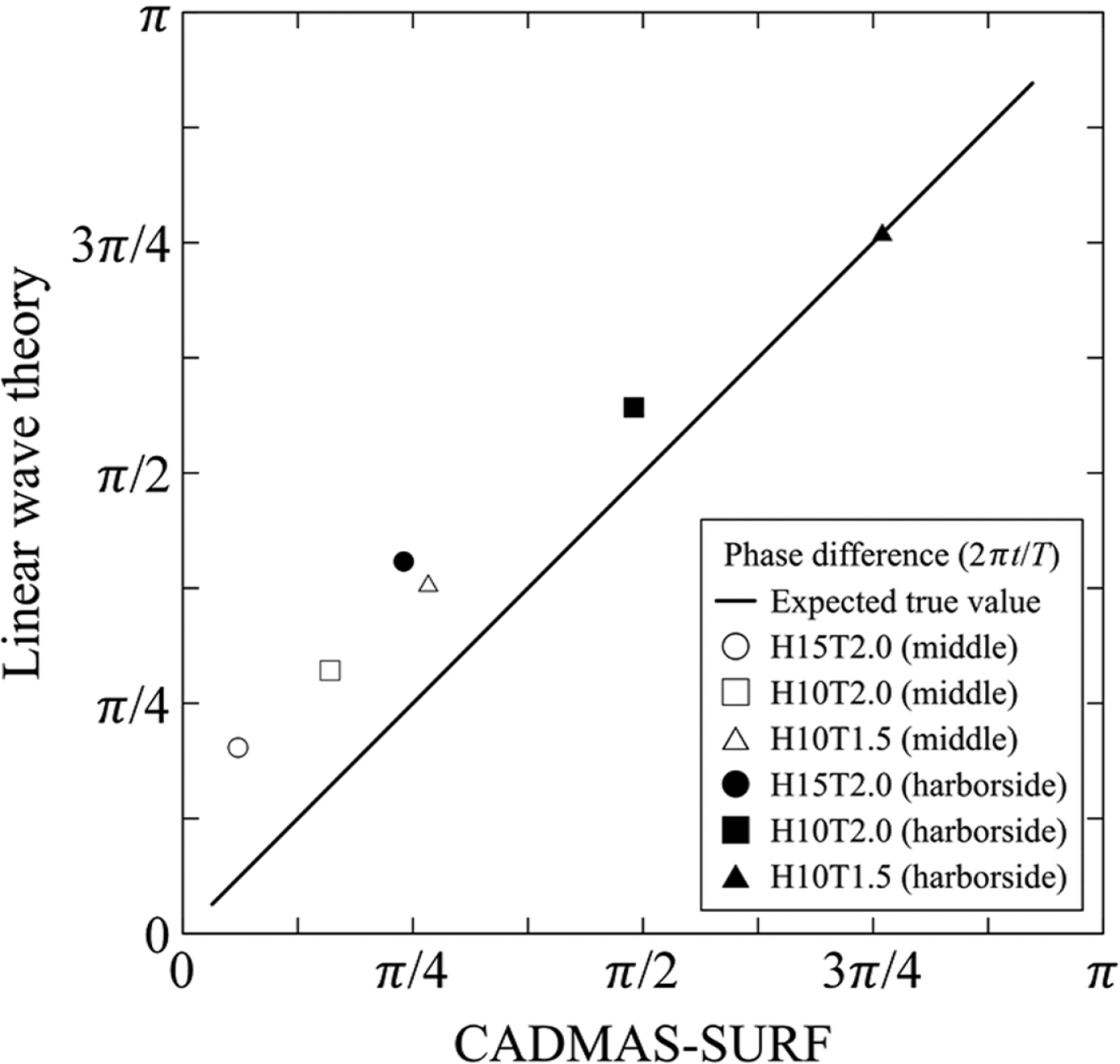
Fig. 10.Time series of wave forces acting on the caisson with the cap concrete (Fc), on the parapet (Fp) and on the breakwater (FT): H = 15 cm, T = 2.0 sec. 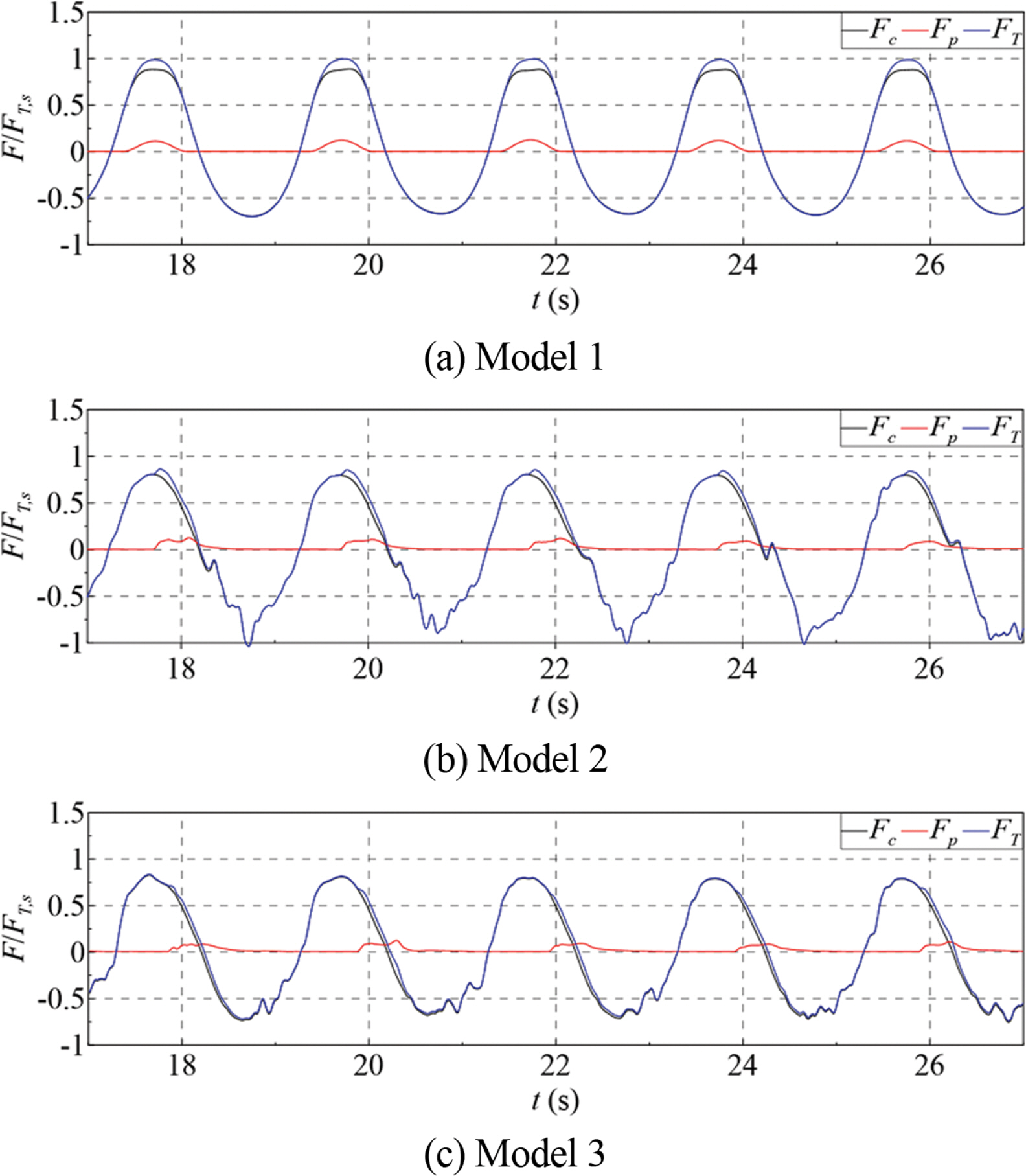
Fig. 11.Time series of wave forces acting on the caisson with the cap concrete (Fc), on the parapet (Fp) and on the breakwater (FT): H = 10 cm, T = 2.0 sec. 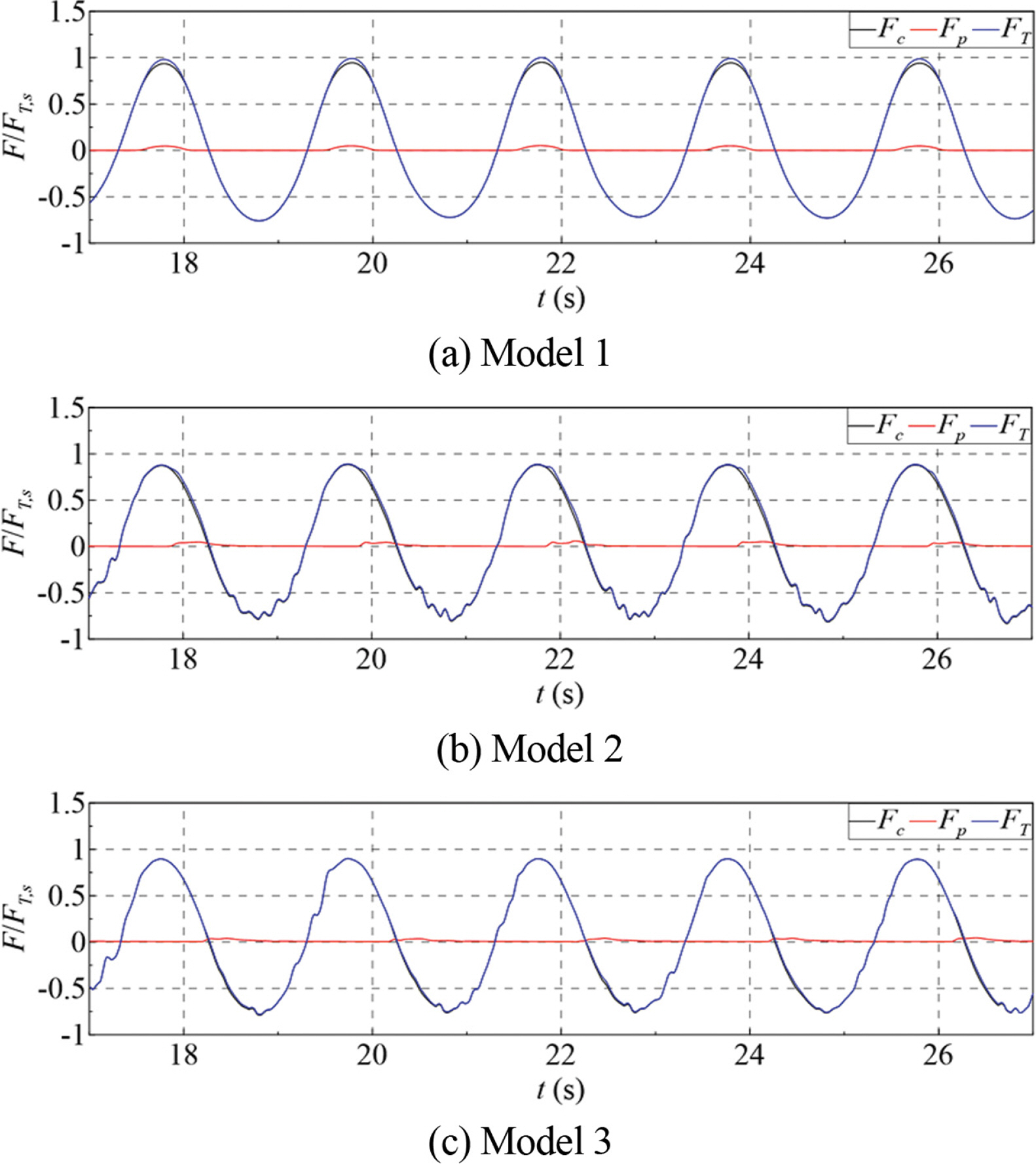
Fig. 12.Time series of wave forces acting on the caisson with the cap concrete (Fc), on the parapet (Fp) and on the breakwater (FT): H = 10 cm, T = 1.5 sec. 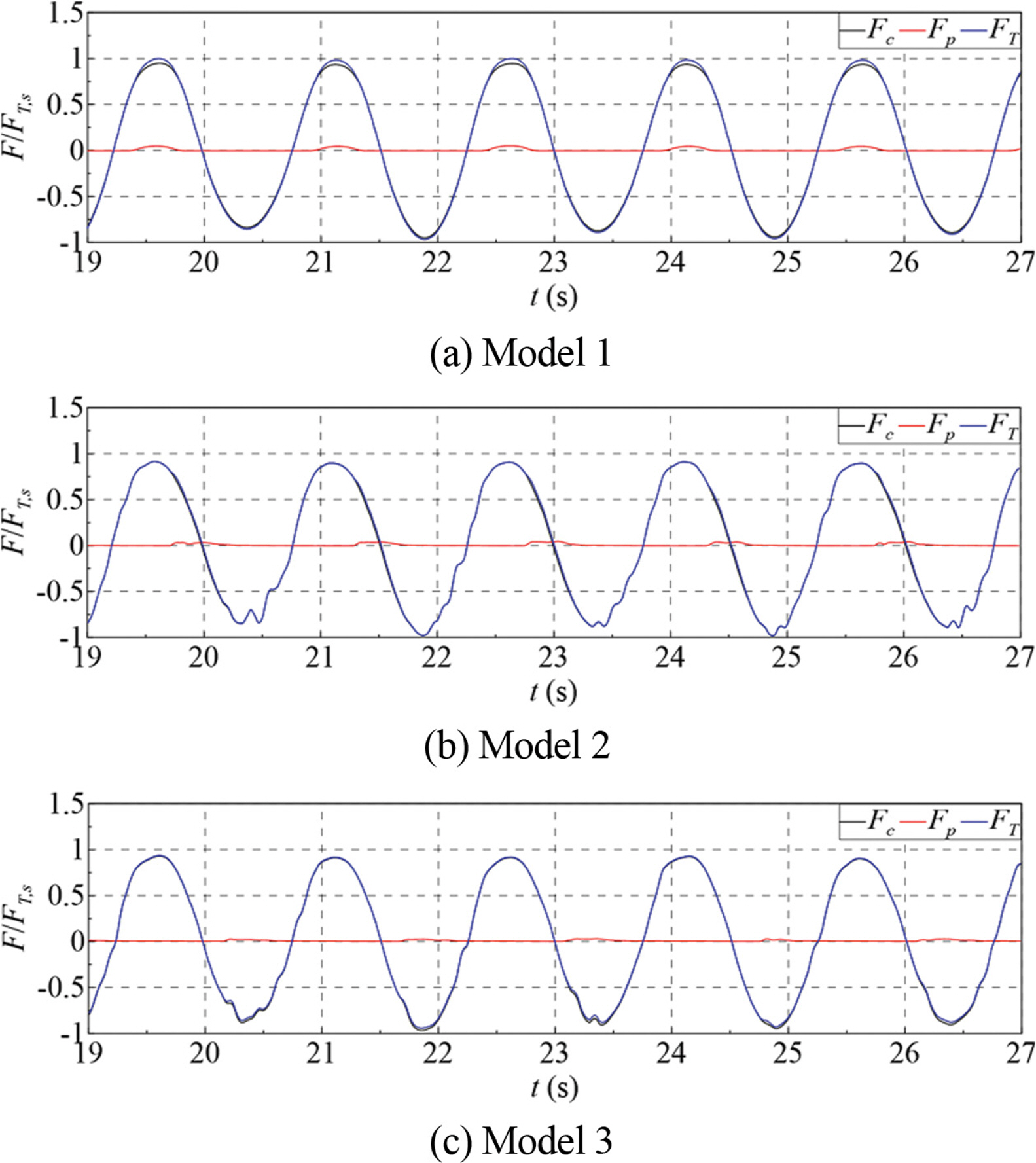
Fig. 13.Pressure distributions (H = 15 cm, T = 2.0 s, h/L = 0.116, H/L = 0.039): (a) Model 1, (b) and (c) Model 3. 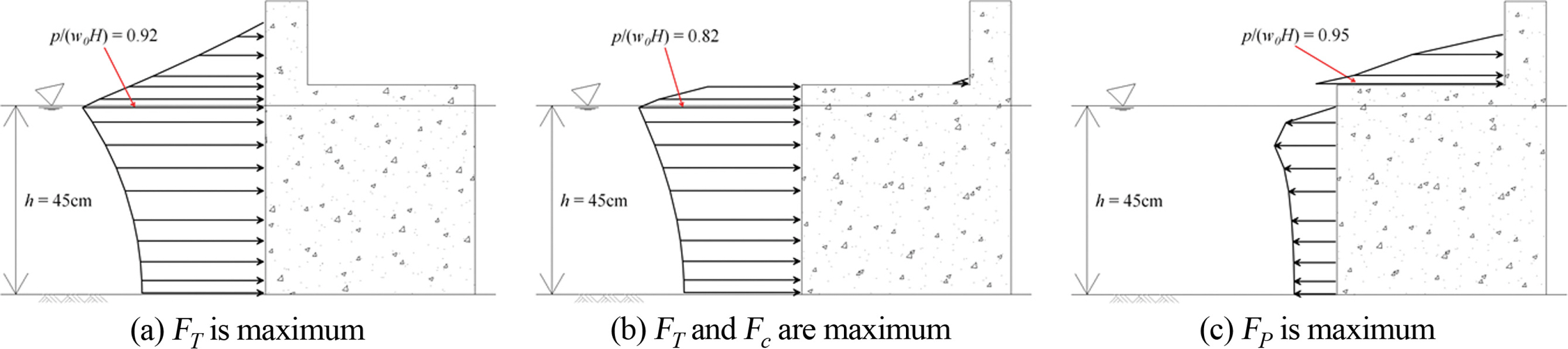
Fig. 14.Pressure distributions (H = 10 cm, T = 2.0 s, h/L = 0.116, H/L = 0.026): (a) Model 1, (b) and (c) Model 3. 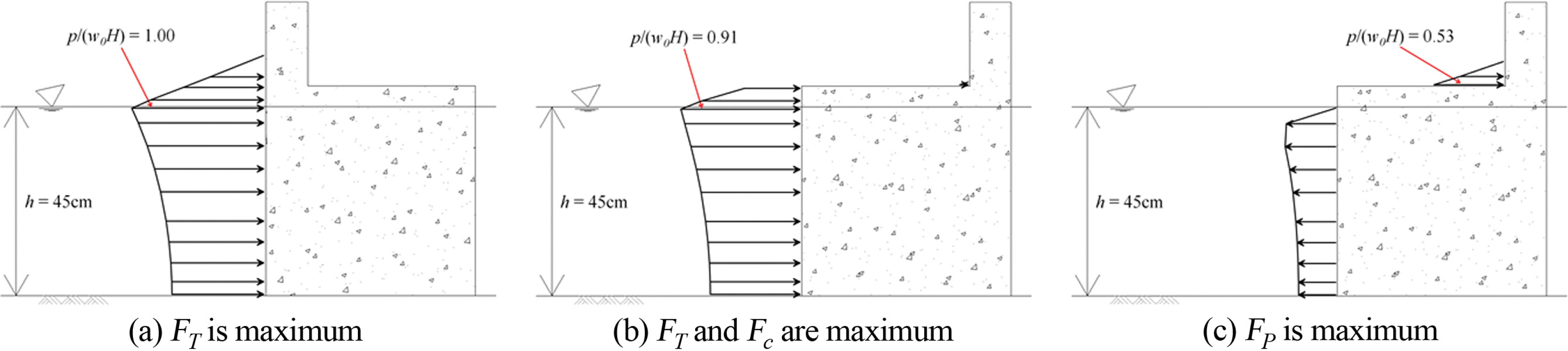
Fig. 15.Pressure distributions (H = 10 cm, T = 1.5 s, h/L = 0.165, H/L = 0.037): (a) Model 1, (b) and (c) Model 3. 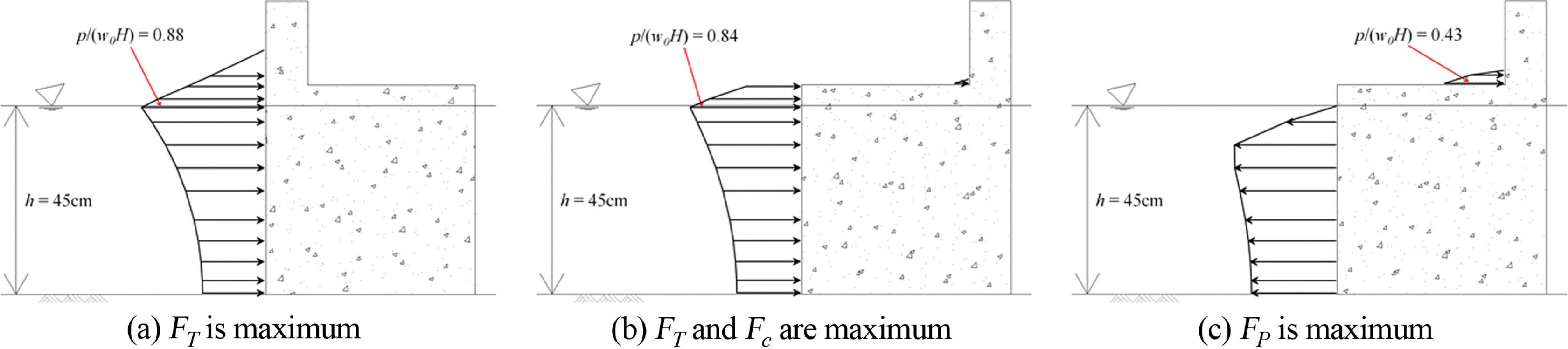
Table 1.Averaged maximum forces with respect to relative parapet locations ReferencesCho, JH, Park, WK, Choe, H, Oh, SB (2018). Research and analysis on reinforcement case of rubble-mound and vertical cassion breakwaters, Proceedings of Korean Society of Civil Engineers, 11-12 (in Korean)..
Coastal Development Institute of Technology (2001). Research and development of numerical wave channel, Coastal Development of Institute of Technology, CDIT Library, (12):(in Japanese)..
Dean, RG (1965). Stream function representation of nonlinear ocean waves, Journal of Geophysical Research, 70(18):4561-4572.
DY Engineering (2013). Report of the working design project of Seogwipo port for the construction to repair damage caused by the typhoon, Jeju Special Self-Governing Province, (in Korean)..
Goda, Y, Kakizaki, S (1966). Study on finite amplitude standing waves and their pressures upon a vertical wall, Report of Port and Harbour Research Institute Ministry of Transport Japan, 5(10):1-57 (in Japanese)..
Goda, Y. (2010). Random seas and design of maritime structures. World Scientific.
Hirt, CW, Nichols, BD (1981). Volume of fluid (VOF) method for the dynamics of free boundaries, Journal of Computational Physics, 39(1):201-225.
Hong, K, Kang, Y-K, Kim, H-J, Yoon, H-S, Ryu, C-R (2018). Analysis of change process in the design conditions of harbor breakwaters in Korea, Journal of Korean Society of Coastal and Ocean Engineers, 30(3):123-133 (in Korean)..
Hyein E&C (2012). Report of the working design project of Gageodo port for the construction to repair damage caused by the typhoon, Ministry for Food, Agriculture, Forestry and Fisheries (MIFAFF), (in Korean)..
IPCC (The Intergovernmental Panel on Climate Change). (2019). Global warming of 1.5°C. Switzerland.
Jung, J-S, Yoon, J-S (2019). Experimental study for over-topping discharges of sea dike having Low Mound and High Wave Wall (LMHW), Journal of Korean Society of Coastal and Ocean Engineers, 31(6):335-343 (in Korean)..
Ko, J-H, Kwon, O-G, Song, S-H, Kim, D-K (2011). Design of construction of contour facilities to improve calmness of Gamcheon harbor, 2011 Conference of the Korean Association of Ocean Science and Technology Societies, 2021-2024 (in Korean)..
Oh, S-H (2016). Analysis of the effect of reducing wave overtopping by wave return walls, Journal of Korean Society of Coastal and Ocean Engineers, 28(1):1-6 (in Korean)..
Sakakiyama, T, Abe, N, Kajima, R (1990). Analysis of nonlinear wave around permeable structure by porous model, Proceedings of Coastal Engineering, JSCE, 37, 554-558 (in Japanese)..
SEKWANG EnC (2018). Report of the working design project of counter facilities of Gamcheon port for the construction to repair damage caused by the typhoon, Ministry of Oceans and Fisheries (MOF), (in Korean)..
Sha, WT, Domanus, HM, Schmitt, RC, Oras, JJ, Lin, EIH (1978). COMMIX-1: A three dimensional transient single-phase component computer program for thermal-hydraulic analysis, Argonne National Laboratory, NUREG/CR-0785, ANL-7796.
Sorensen, RM. (2006). Basic coastal engineering. Springer Science+ Business Media.
Yamada, Y, Satoh, M, Sugi, M, Kodama, C, Noda, AT, Nakano, M, Nasuno, T (2017). Response of tropical cyclone activity and structure to global warming in a high-resolution global non-hydrostatic model, Journal of Climate, 30, 9703-9724.
Yamamoto, Y, Mototama, K, Kamikubo, K (2013). Study on an improvement method for breakwaters at small ports, Research Report, Cold-Region Hydraulic and Aquatic Environmental Engineering Research Group, Public Works Research Institute, (in Japanese)..
|
|
||||||||||||||||||||||||||||||||