Numerical Analysis of the Hydraulic Characteristics of a Boundary Layer Streaming over Beach Cusps Surf-Zone Using LES and One Equation Dynamic Smagorinsky Turbulence Model

Yong Jun Cho

doi:10.9765/KSCOE.2020.32.1.55

Journal of Korean Society of Coastal and Ocean Engineers > Volume 32(1); 2020 > Article

LES와 One Equation Dynamic Smagorinsky 난류모형을 이용한 Beach Cusps 쇄파역에서의 경계층 Streaming 수치해석

Article

J Korean Soc Coast Ocean Eng 2020; 32(1): 55-68.

Published online: February 28, 2020

DOI: https://doi.org/10.9765/KSCOE.2020.32.1.55

LES와 One Equation Dynamic Smagorinsky 난류모형을 이용한 Beach Cusps 쇄파역에서의 경계층 Streaming 수치해석

조용준^*

^*서울시립대학교 토목공학과 교수

Numerical Analysis of the Hydraulic Characteristics of a Boundary Layer Streaming over Beach Cusps Surf-Zone Using LES and One Equation Dynamic Smagorinsky Turbulence Model

Yong Jun Cho^*

^*Professor, Department of Civil Engineering, University of Seoul 163 Seoulsiripdaero, Dongdaemun-gu, Seoul 02504 Korea

Corresponding author: Yong Jun Cho, Professor, Department of Civil Engineering, University of Seoul 163 Seoulsiripdaero, Dongdaemun-gu, Seoul 02504 Korea, Tel: +82-2-6490-2427, Fax: +82-2-6490-2424, young@uos.ac.kr

Received January 18, 2020 Revised February 13, 2020 Accepted February 17, 2020

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted noncommercial use, distribution, and reproduction in any medium, provided the original work is properly cited.

요약

너울이 우세한 온화한 해양환경에서 출현하는 beach cusp에서의 경계층 streaming 수리특성을 살펴보기 위해 edge waves의 천수 과정을 수치 모의하였다. Beach cusp을 유지하는 것으로 알려진 synchronous edge waves는 같은 주기와 파고를 지니는 두 개의 Cnoidal wave가 전면해역에서 비스듬히 조우 되도록 조파하여 재현하였다. Beach cusp의 진폭 A_B과 파장 L_B은 맹방 해변에서 수행된 관측결과를 토대로 각각 1.25 m, 18 m로 선정하였다. 모의결과 천수 각 단계에서 예외 없이 경계층 streaming을 관측할 수 있었으며 최대 경계층 streaming은 사주 정점에서 발생하였다. 주기가 가장 짧은 RUN 1의 경우 그 세기는 약 0.32 m/s 내외에 분포하며 이러한 수치는 free stream 유속 u_∞ 진폭의 두 배에 달하는 것으로 wave Reynolds 응력에 기반한 Longuet-Higgins(1957)의 해석 해와는 상당한 차이를 보였다. 수치 모의과정에서 온화한 해양환경에서 해빈이 복원되는 과정을 특정할 수 있었으며 이 과정을 정리하면 다음과 같다: 너울로 구성된 파랑 무리에서 성분 파랑 간의 공진성 상호작용으로 생성된 외 중력파가 쇄파선 인근에 도달하는 경우 중력으로 인한 가속이 더해진 Phase II 파랑 궤도 운동으로 수면 가까이 상승한 많은 모래가 쇄파 시 발생하는 파 마루로부터 시작된 up-rush에 의해 전 빈 정점 가까이 이동하며 이 과정에서 발생하는 침투로 인해 퇴적되는 것으로 모의 되었다.

핵심용어: beach cusp, synchronous edge wave, 경계층 streaming, LES(Large Eddy Simulation), one equation dynamic smagorinsky 난류모형

Abstract

In order to investigate the hydraulic characteristics of a boundary layer streaming over the beach cusps appeared in swells prevailing mild seas, we numerically simulated the shoaling process of Edge waves over the beach cusp. Synchronous Edge waves known to sustain the beach cusps could successfully be duplicated by generating two obliquely colliding Edge waves in front of beach cusps. The amplitude A_B and length L_B of Beach Cusp were elected to be 1.25 m and 18 m, respectively based on the measured data along the Mang-Bang beach. Numerical results show that boundary layer streaming was formed at every phase of shoaling process without exception, and the maximum boundary layer streaming was observed to occur at the crest of sand bar. In RUN 1 where the shortest waves were deployed, the maximum boundary layer streaming was observed to be around 0.32 m/s, which far exceeds the amplitude of free stream by two times. It is also noted that the maximum boundary layer streaming mentioned above greatly differs from the analytical solution by Longuet-Higgins (1957) based on wave Reynolds stress. In doing so, we also identify the recovery procedure of natural beaches in swells prevailing mild seas, which can be summarized such as: as the infra-gravity waves formed in swells by the resonance wave-wave interaction arrives near the breaking line, the sediments ascending near the free surface by the Phase II waves orbital motion were carried toward the pinnacle of foreshore by the shoreward flow commenced at the steep front of breaking waves, and were deposited near the pinnacle of foreshore due to the infiltration.

Keywords: beach cusp, synchronous edge wave, boundary layer streaming, LES (Large Eddy Simulation), one equation dynamic smagorinsky turbulence model

1. 서론

자연 해빈에서는 해안선이 원호 모양으로 먼바다를 향해 번갈아 가며 나가고 들어오는 것이 흔히 관측되며 이러한 원호 모양의 해안선은 beach cusp이라 불린다. 우리나라 동해안의 여러 백사장 중 아직 개발의 손길이 미치지 못해 자연 해빈에 가깝게 보존된 맹방 해안에서도 상당히 다양한 크기의 beach cusp을 관측할 수 있다(Cho, 2019b; Lee and Cho, 2019).

Beach cusp은 퇴적 성 해빈처럼 간조 단구(low tide terrace)와 해안 사이에 급경사의 전 빈이 형성되는 경우 전빈 수주에서 자극된 sub-harmonic edge waves에 의해 해빈 표사가 재배치되는 과정에서 생성된다(Guza, 1974). 전술한 subharmonic edge waves는 해안에 beach cusp이라는 흔적을 남기고 소멸하며, 이렇게 초기화된 beach cusp은 내습하는 파랑과 같은 주기를 지니는 synchronous edge waves에 의해 유지된다(Guza, 1974; Cho, 2019b; Lee and Cho, 2019).

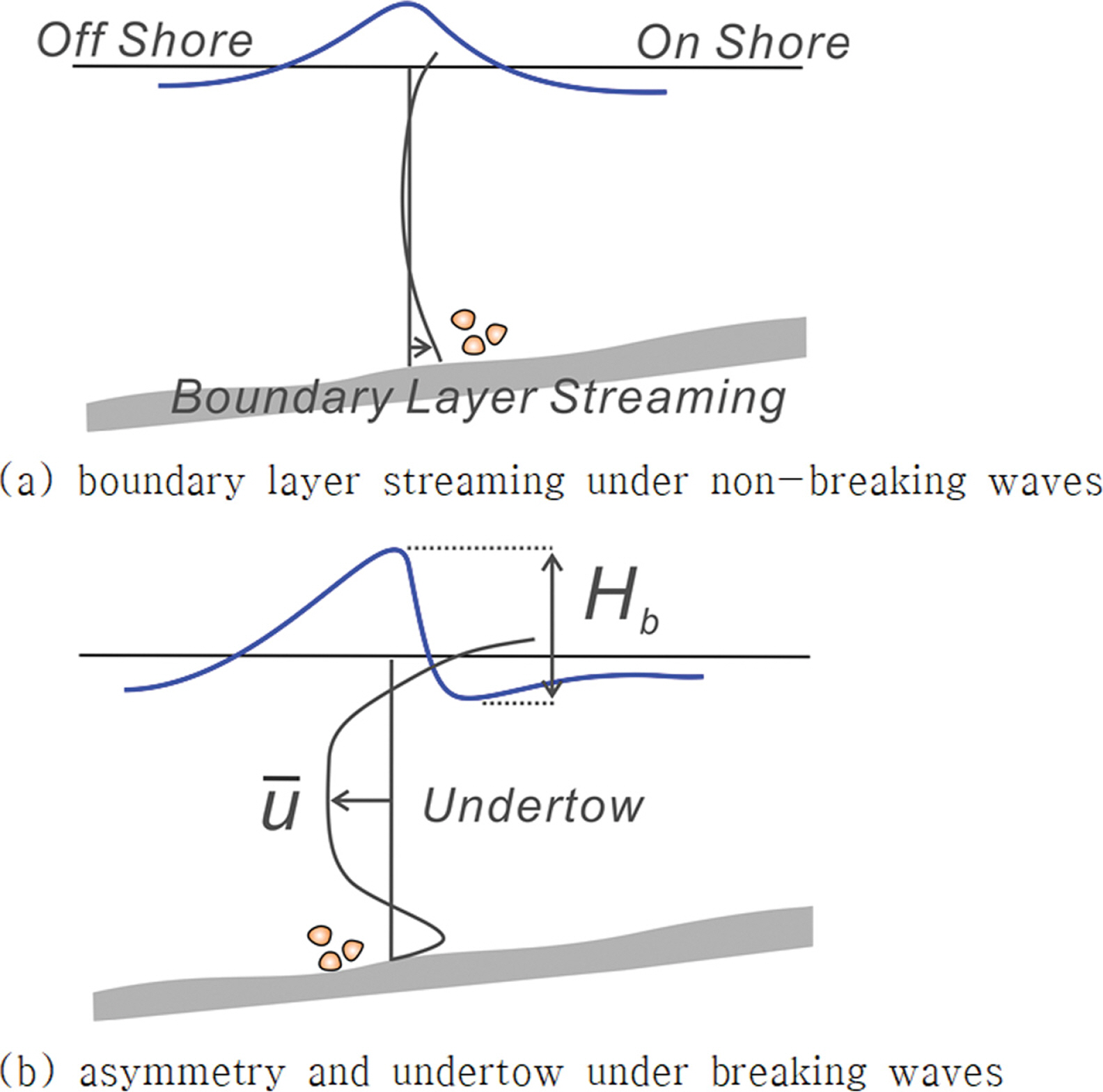
자연 해빈은 고 파랑에 의해 해빈이 대규모로 침식되더라도 폭풍이 잦아들고 너울이 우세한 해양환경이 회복되는 경우 점진적으로 복원되며, 이러한 해빈 복원은 경계층 streaming을 통해 이루어진다(Cho and Kim, 2019; Cho et al., 2019; Cho, 2019a).

온화한 해양환경 혹은 다소 거친 모래로 구성된 해빈이 장주기 파랑에 노출되는 경우 형성되는 퇴적 성 해빈은 Dean Number Ω<1로 분류되며 좁은 해빈 폭, 급한 전빈 경사, swash 대역에서 형성되는 beach cusp, 원 빈에 형성된 사주와 같은 성정을 지닌다. 이에 반해 Ω>6으로 분류되는 침식성 해빈은 거친 해양환경, 고운 모래로 구성된 해빈, 완만한 전빈 경사, 소멸한 사주와 같은 성정을 공유한다.

전술한 퇴적 성 해빈의 성정에서 유추할 수 있듯 온화한 해양환경에서 해빈에 모래가 쌓이는 과정을 정리하면 다음과 같다:

Stokes drift에 의해 부유사 형태로 해안 가까이 이송된 표사는 후행하는 처 오름 과정에서 온화한 해양환경에서 낮아진 지하 수위로 인해 흐름 일부분이 침투되는 과정에서 전 빈에 퇴적된다. 이에 반해 침투되지 못한 나머지 흐름은 처오름 정점에서 방향을 틀어 먼바다 방향으로 회귀 되며 이렇게 형성된 흐름(under-tow)은 사면을 따라 가속되며 이 과정에서 전 빈 기부를 구성하는 모래 중 일부는 부유사 혹은 소류사 형태로 under-tow와 함께 먼바다 방향으로 쓸려간다. 먼바다 방향으로 수심이 깊어짐에 따라 under-tow의 범위는 증가하나 그 세기는 점점 약해지며 함께 쓸려온 모래는 퇴적되어 원 빈에 사주가 형성된다. 수심이 깊어짐에 따라 저류의 세기가 약해지며 수주에 순 유입된 흐름은 방향을 틀어 자유수면을 향해 진행되며 이렇게 형성된 상승류는 원 빈에서 흔히 관측되는 사주 형성과 형성 위치를 결정하는 중요한 기작으로 기능한다(Cho, 2019c).

이상의 논의에서 알 수 있듯, beach cusp, 해안에 쌓이는 모래, 원빈 사주는 파랑으로 인해 해빈 모래가 재분배되는 과정으로 해석되어야 한다. 전술한 현상 중 beach cusp은 해빈 대순환과정 중 해빈 복원을 구성하는 중요한 요소라는 점에서 beach cusp swash zone에서의 경계층 streaming 수리특성을 살펴보는 작업은 상당한 공학적 가치를 지니며(Fig. 1 참조), 해빈 침식 대응방안 최적화 과정에서도 적지 않은 역할을 담당할 수 있을 것으로 판단된다(Cho, 2019b).

이러한 인식에 기초하여 본 논문에서는 너울이 우세한 온화한 해양환경에서 출현하는 beach cusp에서의 경계층 streaming 수리특성을 살펴보기 위해 전면해역에 사주를 지닌 beach cusp에서의 천수 과정이 수치 모의 된다. Beach cusp을 유지하는 기작으로 알려진 synchronous edge waves는 beach cusp 전면해역에서 비스듬히 만나는 두 개의 Cnoidal waves를 조파하여 재현되며(Lee and Cho, 2019), 비교를 위해 영의 영각으로 진입하는 Cnoidal waves의 천수 과정 수치 모의도 병행하여 수행된다. 수치 모의는 spatial averaging filter를 활용하여 차용된 격자보다 작은 규모의 난류는 등방성에 근접한다는 시각에서 LES(Large Eddy Simulation), 잔차 응력(residual stress)은 one equation dynamic Smagorinsky 난류모형을 활용하여 수행되며, 이 과정에서 파랑모형은 spatially filtered Navier-Stokes Eq.과 질량 보존 식으로 구성된다. LES 난류모형에서 평균 흐름과 비슷한 규모로 평균 흐름으로부터 유동 에너지를 추출하는 큰 규모의 와는 직접 모의 된다. 이에 반해 비교적 등방성에 가까운 부 관성 대역(inertial sub-range)에 분포하는 작은 규모의 와는 모형을 통해 수치 모의 된다는 면에서 기존의 RANS(Reynolds Averaged Navier-Stokes Eq.)에서의 eddy viscosity 기울기 모형보다 우월성을 지닌다(Pope, 2004). 이러한 SPS(Sub Particle Scale) 난류모형은 DNS(Direct Numerical Simulation)에 견줄만한 정도를 제공한다(Cho and Lee, 2007; Cho and Kim, 2008; Cho et al., 2008; Meneveau et al., 1996).

2. 맹방 해빈 Beach Cusp의 생성과정

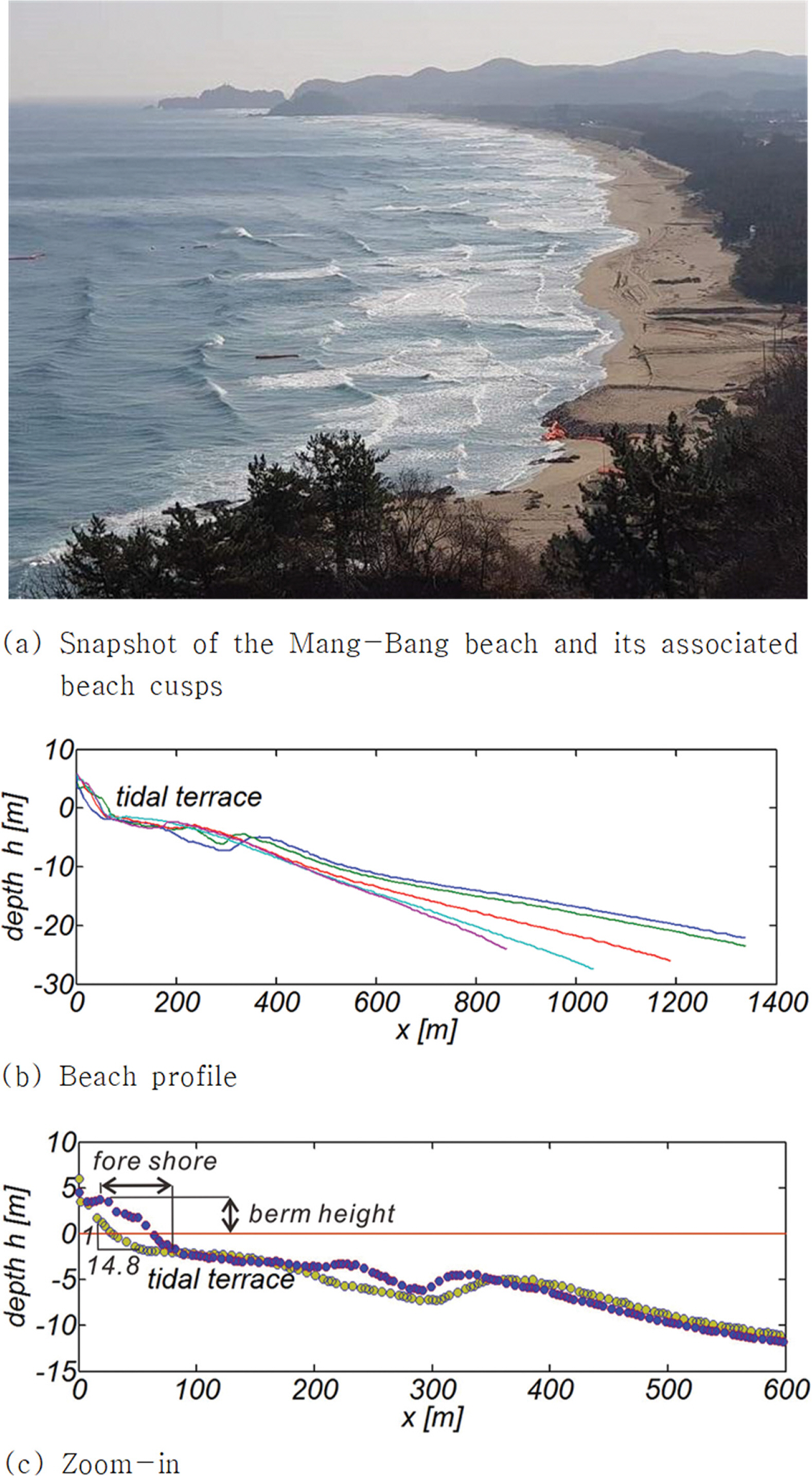
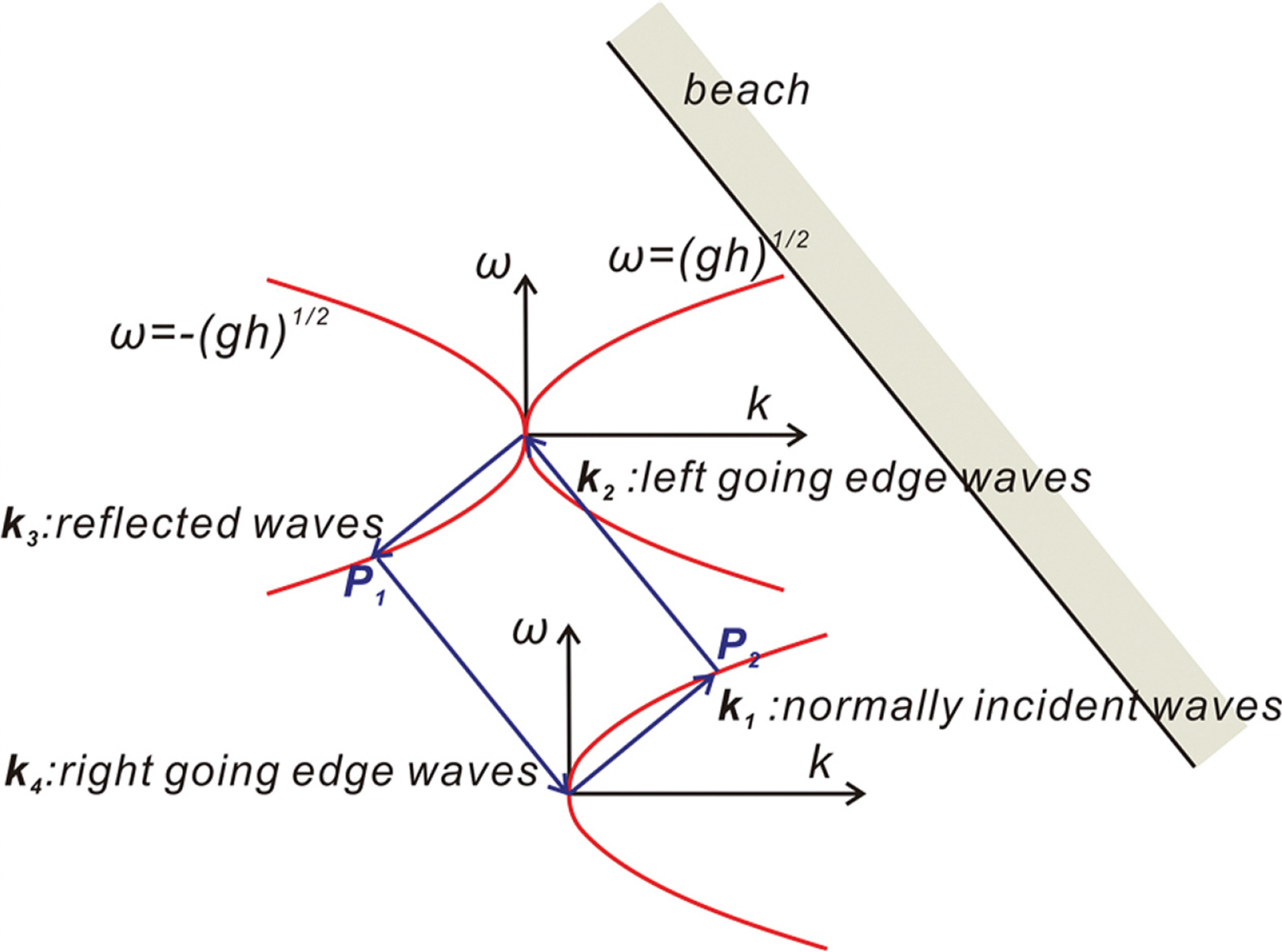
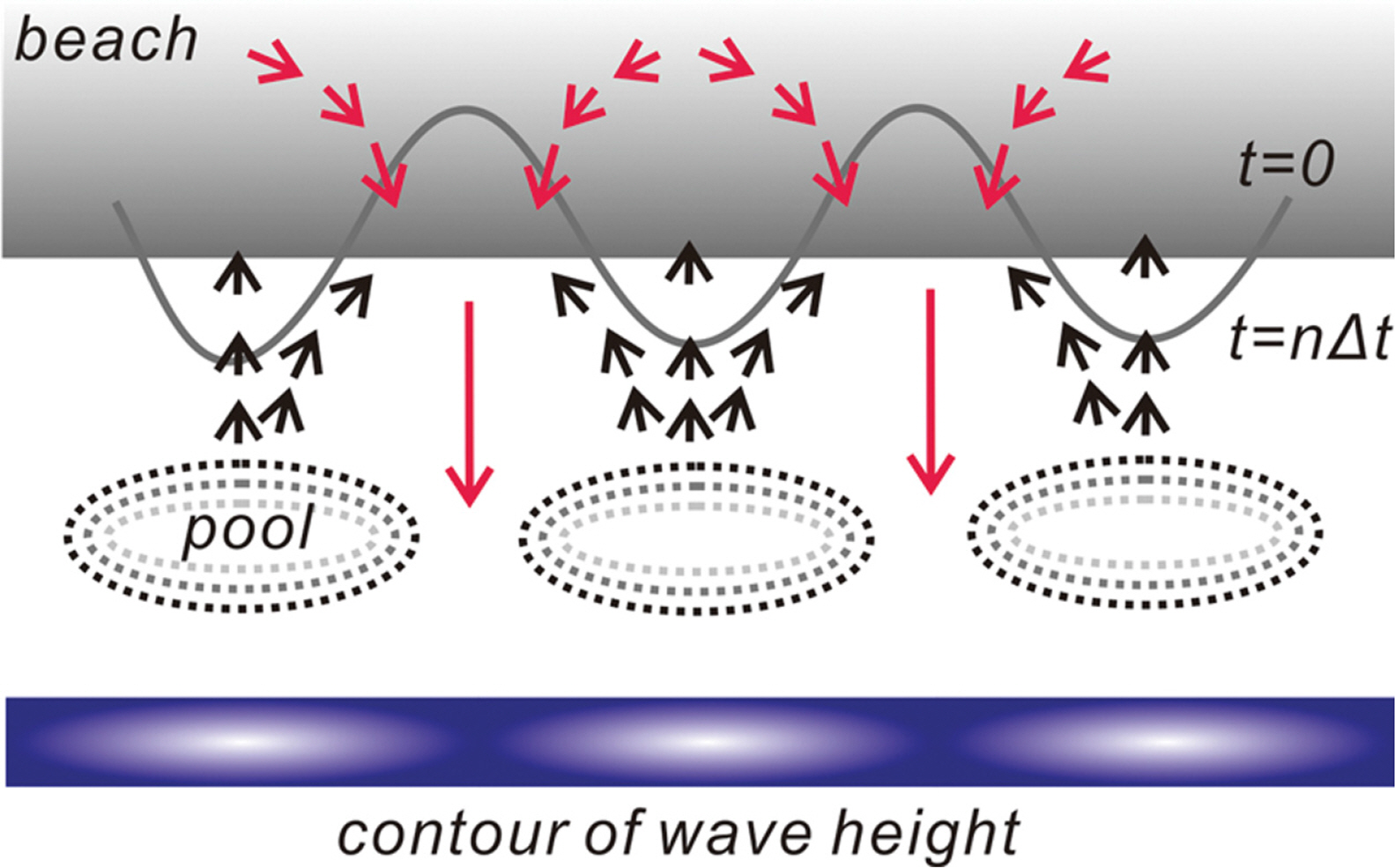
최근 해안공학 계에서는 beach cusp은 edge waves에 의해 결과되는 것으로 보는 시각이 주류를 이룬다. Beach cusp의 생성기작으로 edge waves의 가능성을 맨 처음 제기한 이는 Guza(1974)로, Guza(1974)의 연구결과에 따르면 퇴적성 해빈처럼 간조 단구(low tide terrace)와 해안 사이에 경사가 1/10 내외인 급경사의 전 빈이 형성되는 경우(Fig. 2 참조) 전빈 수주의 고유 운동 mode 중 하나인 edge waves가 쉽게 자극될 수 있는 해양환경이 마련된다. 가장 쉽게 자극될 수 있는 Edge waves 주기는 입사파 주기의 2배로 이는 Hasselmann(1967), Phillips(1980) 이후 해안공학 계에서 풍성 파의 성장과정과 관련하여 잘 알려진 sub-harmonic resonance와 결을 같이한다. 영의 영각으로 내습하는 외 중력파에 상당한 세기의 반사파가 더해져 정상 파동 계가 전 빈에 형성되고, 이어 정상 파동 계를 구성하는 외 중력파 사이에 resonance triad 혹은 quartet(Fig. 3 참조)가 충족되는 경우 출현하는 포획 상태 edge waves에 의해 beach cusp은 초기화된다(Lee and Cho, 2019). 전술한 sub-harmonic edge waves는 해안에 beach cusp이라는 흔적을 남기고 소멸하며, 이렇게 초기화된 beach cusp은 내습하는 파랑과 같은 주기를 지니는 synchronous edge waves에 의해 유지된다(Fig. 4 참조).

맹방 해빈은 해안선으로부터 60~80 m 떨어진 지점까지 경사가 1/10 내외인 급경사의 전 빈이 포진하며 이후 수심이 5 m 내외인 간조 단구(low tide terrace)가 해안으로부터의 거리가 200 m인 지점까지 길게 이어진다. 최근 Cho(2019b)는 Eckart(1951)와 Guza(1974)의 천수 방정식 해석 해에 기초하여 전술한 맹방 해빈 전빈 폭으로부터 맹방 해빈에 출현할 수 있는 포획 모드 edge waves의 주기와 resonance quartet을 구성하는 입사파 주기를 가늠하고, 포획 모드 edge waves를 초래하는 입사파는 주기는 38.9s 내외인 외 중력파로 특정한 바 있다.

Cho(2019b)의 연구결과에 따르면 맹방 해안에서 형성되는 beach cusp은 다수의 sand wave가 하나로 융합되는 과정과 이렇게 융합된 하나의 커다란 sand wave가 다시 여러 개의 작은 sand wave로 나뉘는 과정이 반복된다. 또한, 고 파랑에 의한 대규모 침식으로 해빈이 재정렬되는 과정에서 역동적인 모양의 beach cusp은 소멸하며, Spectral mean sand wave NO의 시계열 자료로부터 가늠하는 경우 beach cusp의 대순환과정은 일 년에 두 번에 걸쳐 진행된다.

3. 수치모형

3.1 파랑모형

LES에서의 파랑모형은 Navier-Stokes 방정식을 spatial averaging filter를 적용하여 여과하는 경우 얻게 되며, 이렇게 유도된 운동량 방정식과 연속방정식을 기술하면 각각 다음과 같다.

(1)

∂u¯i∂xi=0

(2)

∂u¯i∂t+∂∂xjUiUj¯=−1ρ∂p¯∂xi+v∂2u¯i∂xj∂xj

식(2)에서 ρ는 물의 밀도, ν는 물의 동점성 계수, p¯는 공간 여과된 수정 압력, u¯는 여과 속도(filtered velocity), U=u¯+u'는 순간속도를 각각 나타낸다. 식(2)의 좌측 두 번째 항을 여과 속도 u¯와 잔차 속도(residual velocity) u'으로 구분하는 경우 다음과 같이 기술될 수 있으며,

(3)

UiUj¯=u¯iu¯j¯+u′u¯j¯+u¯iuj'¯+ui'uj'¯

식(3)의 우측 오른쪽 3개 항은 여과 과정(spatial averaging)에서 발생하는 잔차 응력(residual stress)을 나타낸다. 전술한 잔차 응력을 τRij라고 정의하면 식(2)의 좌측 두 번째 항은 다음과 같이 기술될 수 있다.

(4)

∂∂xj(UiUj¯)=∂∂xj(ui'¯uj'¯)+∂∂xj(τRi¯j)

식(4)의 τRij는 비등방성 잔차 응력 τijr을 활용하는 경우 다음과 같이 기술될 수 있으며

(5)

τijR=τijr+23ksgsδij

여기서δ_ij는 Kronecker delta, k_sgs는 sub-grid scale의 운동에너지를 각각 나타내며 k_sgs는 다음과 같이 기술될 수 있다.

(6)

ksgs=12τkk=12(ukuk¯−ukuk¯)

식(2)에 식(4), (5)를 대입하고 정리하면 LES 운동방정식은 다음과 같이 기술될 수 있다.

(7)

∂ui'¯∂t+∂∂xj(ui¯uj¯)=−1ρ∂p¯∂xi+ν∂2ui¯∂xj∂xj−∂τijr¯∂xj

3.2 Subgrid-scale 난류모형 중 one equation dynamic Smagorinsky 난류모형

식(7)에 기술된 지배방정식을 완결하기 위해서는 여과 과정에서 발생한 비등방성 잔여 응력 항을 모형화할 필요가 있으며 문헌에서 자주 언급되는 Smagorinsky(1963) 모형을 기술하면 다음과 같다.

(8)

τijr=−2νsgsSij¯

여기서 v_sgs는 잔여 유속의 난류 점성계수, Sij¯는 여과 속도에 의한 변형률을 각각 나타내며 Sij¯는 다음과 같이 정의된다.

(9)

Sij¯=12(∂ui¯∂xj+∂uj¯∂xi)

식(8)에서 난류 점성계수 v_sgs 는 다음과 같이 기술될 수 있으며,

(10)

νsgs=CSksgsΔ

여기서 C_S는 Smagorinsky 계수로 일반적인 전단 흐름의 경우 0.065~0.1 사이의 값을 지니며, 본 논문에서는 0.094를 사용하였다.

식(10)에서 쇄파 역에서의 난류 에너지의 국지적 생성, 확산, 소산은 k_sgs에 대한 이송방정식을 추가로 도입하는 경우 설명될 수 있으며 k_sgs 이송방정식을 기술하면 다음과 같다(Yoshizawa and Horiuti, 1985).

(11)

∂(ρksgs)∂t+∂∂xj(ρuj¯ksgs)−∂∂xj[ρ(ν+νsgs)∂∂xj(ksgs)] =−ρτij:Sij¯−Cɛρksgs3/2Δ

식(11)에서 ν=μ/ρ는 동점성 계수, C_ε는 경험계수, △=(△_x△_y△_z)^1/3, △_x, △_y, △_z는 각 방향의 필터 크기를 각각 나타내며, 난류 에너지의 생성을 의미하는 -ρτij : Sij¯는 다음과 같이 기술될 수 있으며,

(12)

−ρτij:Sij¯=−23ρksgs∂uk¯∂xk+ρvsgs∂ui¯∂xj(2Sij¯−13tr(2S¯)δij)

여기서 S¯는 여과된 특성 변형률을 나타내며 다음과 같이 정의된다.

(13)

S¯=(2Sij¯Sij¯)1/3

4. 수치 모의

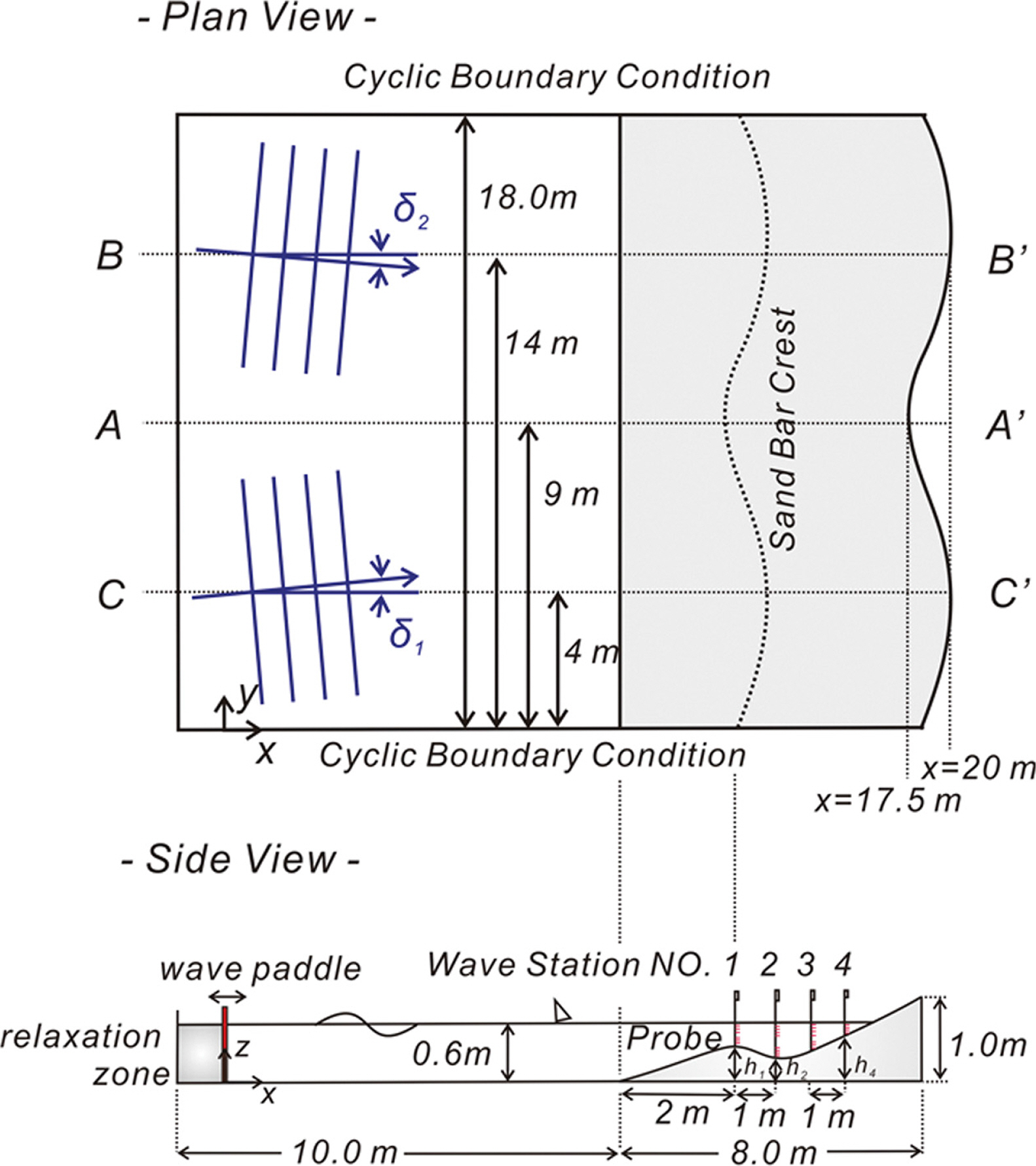
너울이 우세한 온화한 해양환경에서 출현하는 beach cusps에서의 경계층 streaming 수리특성을 살펴보기 위해 전면해역에 사주를 지닌 해빈에서의 edge waves 천수 과정을 수치 모의하였으며 beach cusp의 진폭 A_B과 파장 L_B은 맹방 해변에서 수행된 관측결과(Cho, 2019b)를 토대로 각각 1.25 m, 18 m로 선정하였다(Fig. 5, 6 참조).

Beach cusp을 유지하는 것으로 알려진 synchronous edge waves는 같은 주기와 파고를 지니는 두 개의 Cnoidal wave가 전면해역에서 비스듬히[θ = π - δ₁ - δ₂ = 140º] 조우 되도록 조파하여 재현하였다. 이 경우 결과되는 파동 계는 연안 방향으로 파고가 변조되는 short-crested waves로 synchronous edge waves와 같은 성정을 지니며, 비교를 위해 영의 영각으로 진입하는 Cnoidal waves의 천수 과정 수치 모의도 병행하여 수행하였다(Fig. 5 참조).

수치 모의는 OpenFoam 기반 Tool box인 IHFoam을 사용하여 수행하였으며(Losada et al., 2008; Cho and Bae, 2019), 파랑모형은 spatially filtered Navier-Stokes Eq.과 질량 보존식으로 구성하였다. 자유수면은 VOF(Volume Of Fraction)법을 활용하여 추적하였으며, 바닥에는 no-slip boundary condition, 측면에는 cyclic boundary condition을 적용하였다. 난류모형으로는 차용된 격자보다 작은 규모의 난류는 등방성에 근접한다는 시각에서 LES(Large Eddy Simulation), 잔차응력(Residual Stress)은 one equation dynamic Smagorinsky 모형을 활용하여 모의하였다.

Numerical wave basin은 Fig. 5에 정리하였으며, 도시된 계산영역은 1,250,000개의 절점으로 이산화하였다. Beach Cusps 쇄파 역과 포말대에서의 경계층 streaming의 수리특성을 살펴보기 위해 주기를 바꿔가며 총 6번의 수치 모의를 수행하였으며, Table 1에는 수치 모의에 사용된 해빈 경사, 파랑 조건, 해빈 형태 등을 정리하였다.

5. 수치 결과

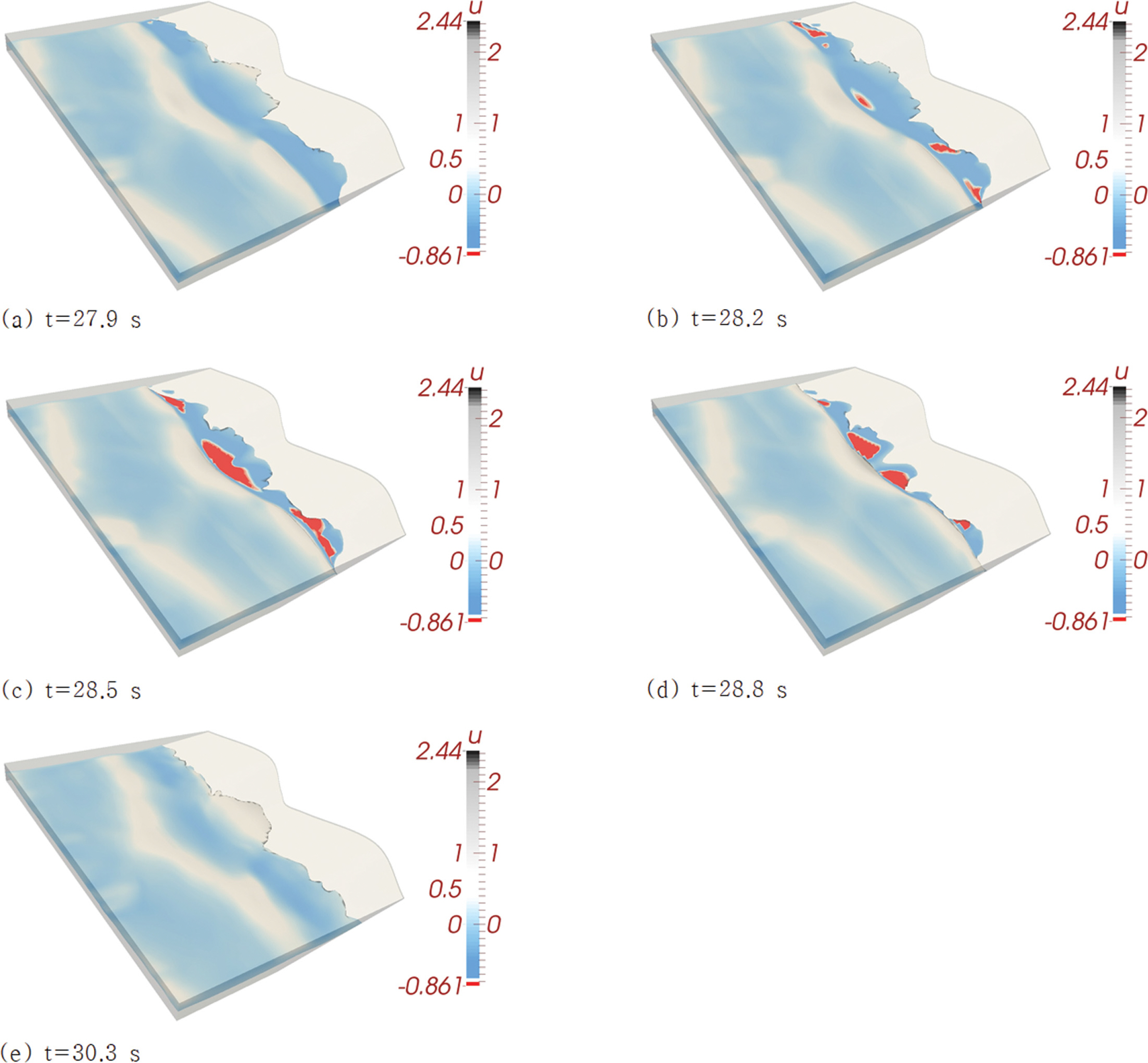
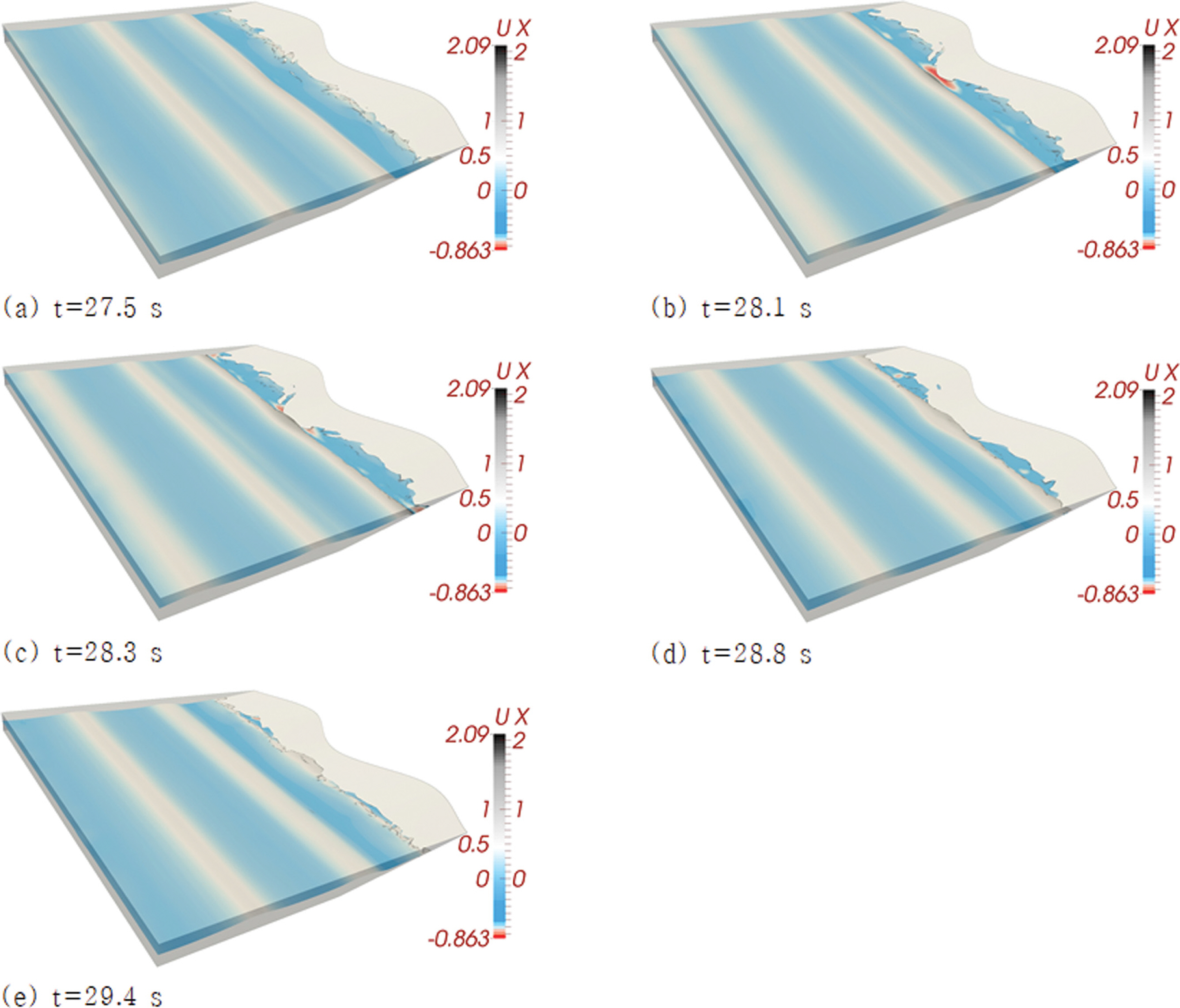
Fig. 7에는 RUN 4 수치 모의과정에서 관측된 자유 수면을, Fig. 8에는 유속 벡터 도를 차례대로 도시하였으며 천수 단계별 특성을 확연히 드러내기 위해 한 주기를 각각 다섯 개와 여섯 개의 frame으로 구성하였으며, RUN 6에서 관측된 자유 수면은 Appendix A에 수록하였다.

비스듬히 조우하는 두 개의 Cnoidal waves로 구성된 short-crested의 파랑이 beach cusp의 정점을 통과하는 경우 예상해 볼 수 있는 수리 현상이 상당한 정도로 모의 되는 것으로 판단되며 이러한 판단은 다음과 같은 관측결과에 준거한다.

A. Beach cusp 돌출부에서 발생하는 처 오름 정점에서 양쪽에 자리한 파랑 분산 영역으로 나뉘어 진행되는 backwash를 Fig. 7(c), Fig. 7(d), Fig. 8(b), Fig. 8(c) 등에서 관측할 수 있다.

B. 파랑이 집중되는 beach cusp 돌출부에서의 처 오름 높이가 파랑이 분산되는 beach cusp 만입 부에서의 처 오름 높이보다 상대적으로 크게 관측된다[Fig. 7(a) 참조].

Fig. 9, 10에는 RUN 3, 4에서 관측된 계산영역을 가로지르는 단면 A - A'에서의 유속 벡터 도를 천수 단계별로 정리하였다. 사주 배후 수역에서 진행되는 surging 형태의 쇄파와 선행 파랑에 의한 처 오름 과정을 명징하게 관측할 수 있다. 여기서 한 가지 흥미로운 현상은 선행 파랑에 의한 처 오름과 후행하는 파랑 선단부 사이 해역에서 관측되는 먼바다 방향의 흐름으로 중력에 의한 가속으로 겉보기에는 처 내림처럼 보이나 잘 갖추어진 파랑 운동의 한 부분으로 해석되어야 할 것으로 판단된다(Fig. 9, 10 참조). 이러한 시각은 전술한 해역이 파 곡(wave trough)에 해당하며 파 곡에서의 흐름은 먼바다 방향으로 진행된다는 사실을 상기하면 쉽게 이해될 수 있으며 전술한 해역에서의 유속이 Phase II을 거쳐 Phase III (Fig. 11(a) 참조)로 점진적으로 변환되는 수치 모의결과에서도 확인할 수 있다(Fig. 9, 10, 11 참조).

또 한 사주 배후 수역에서 진행되는 쇄파는 RUN 3보다 주기가 상대적으로 긴 RUN 4에서 먼저 시작되며 쇄파 형태도 더 역동적으로 보이며, 이와 더불어 처 오름 높이도 더 크다는 것을 알 수 있다. 이러한 현상은 장파가 단파보다 저면 영향을 더 일찍 받는다는 사실과 주기가 길수록 평균 수면 위에 포진하는 수주 체적이 증가한다는 사실을 상기하면 수용 가능해 보인다.

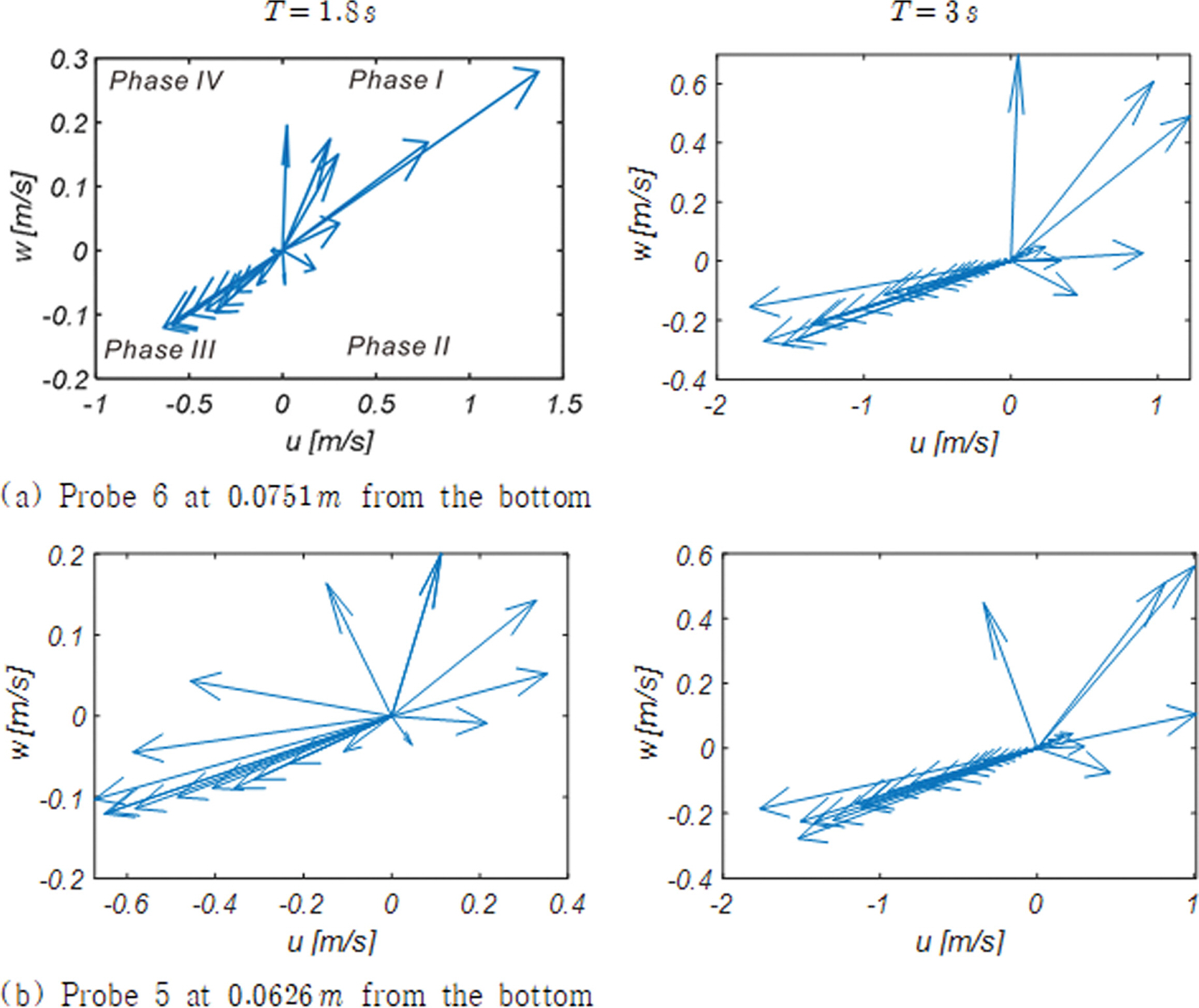
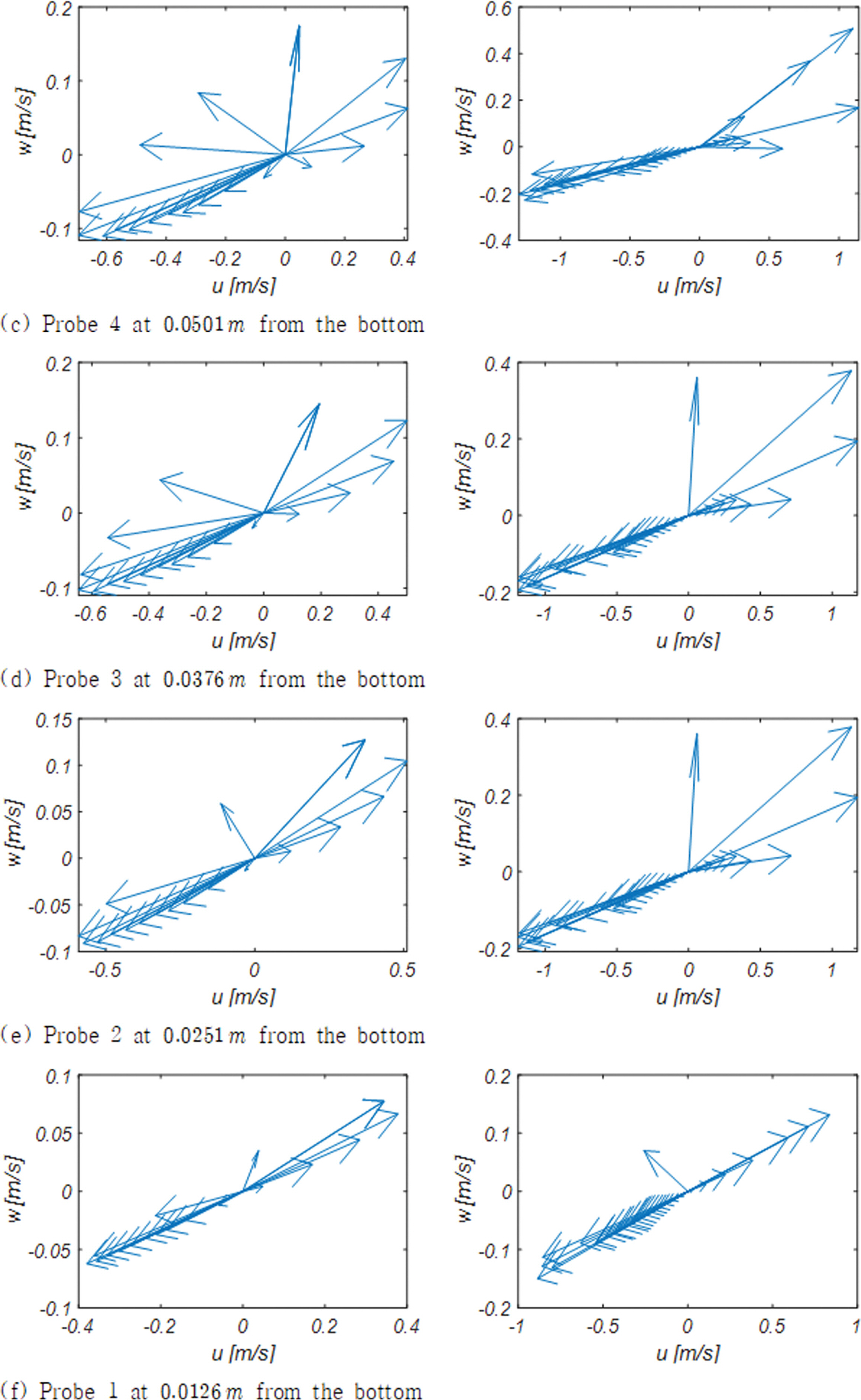
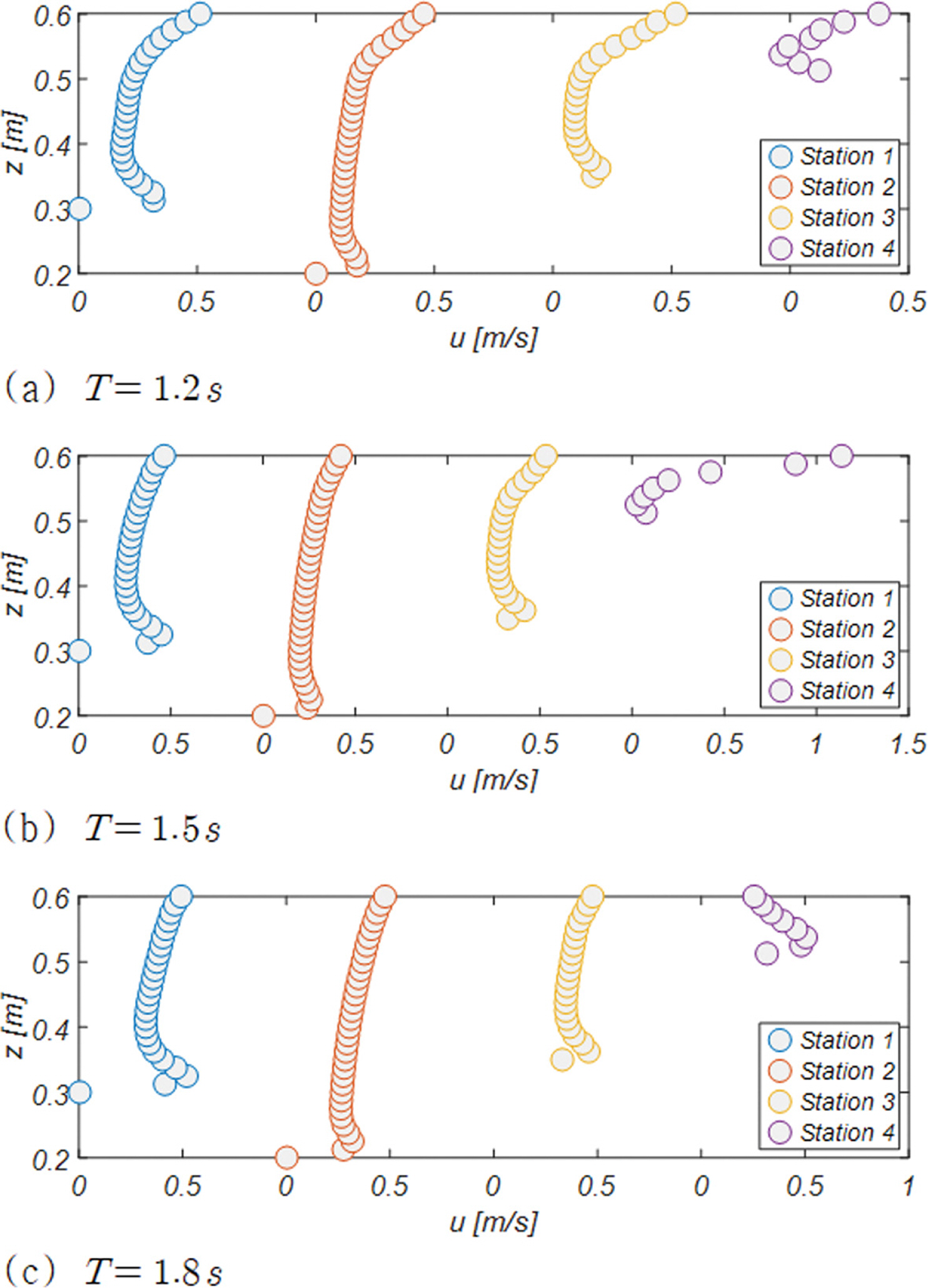
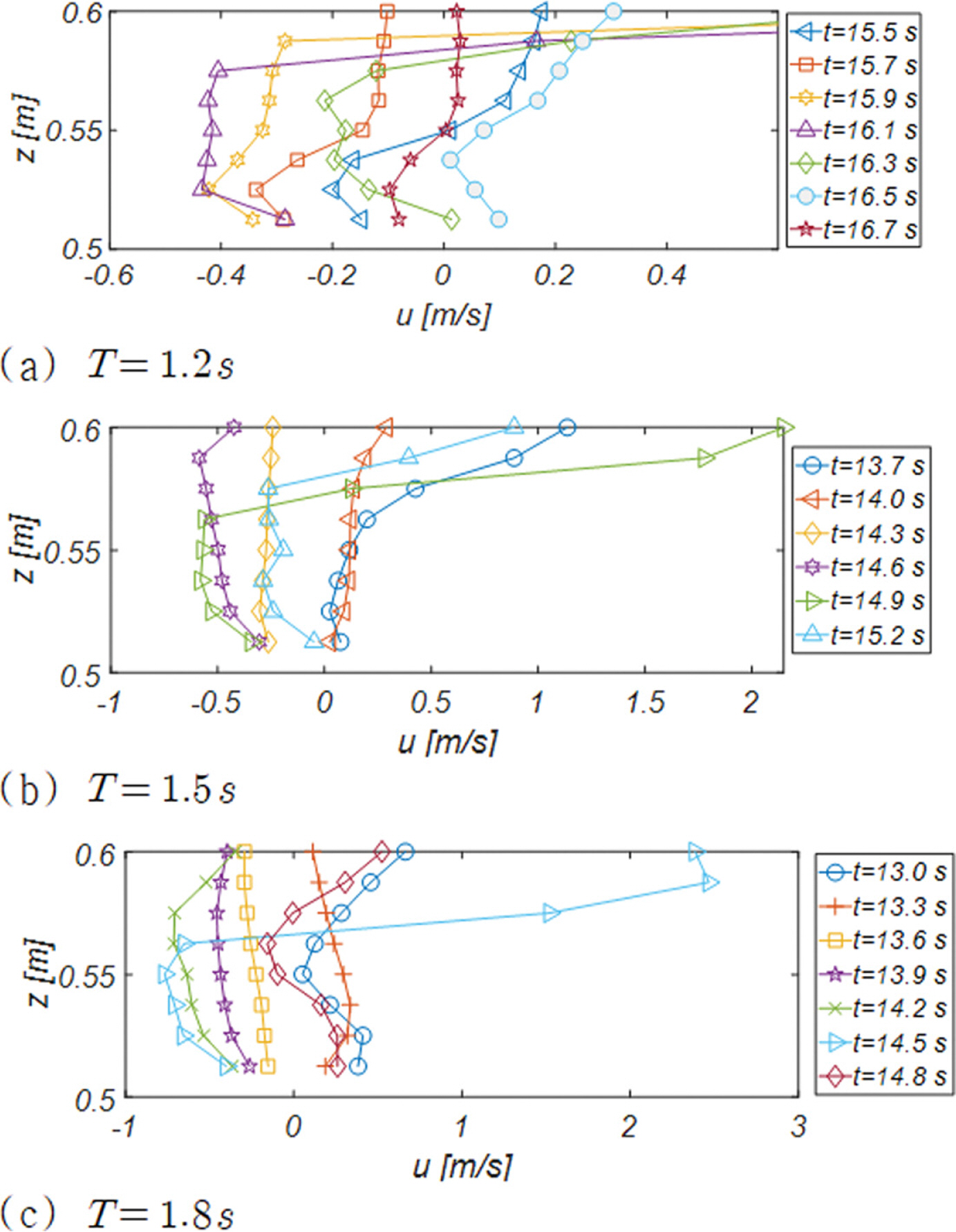
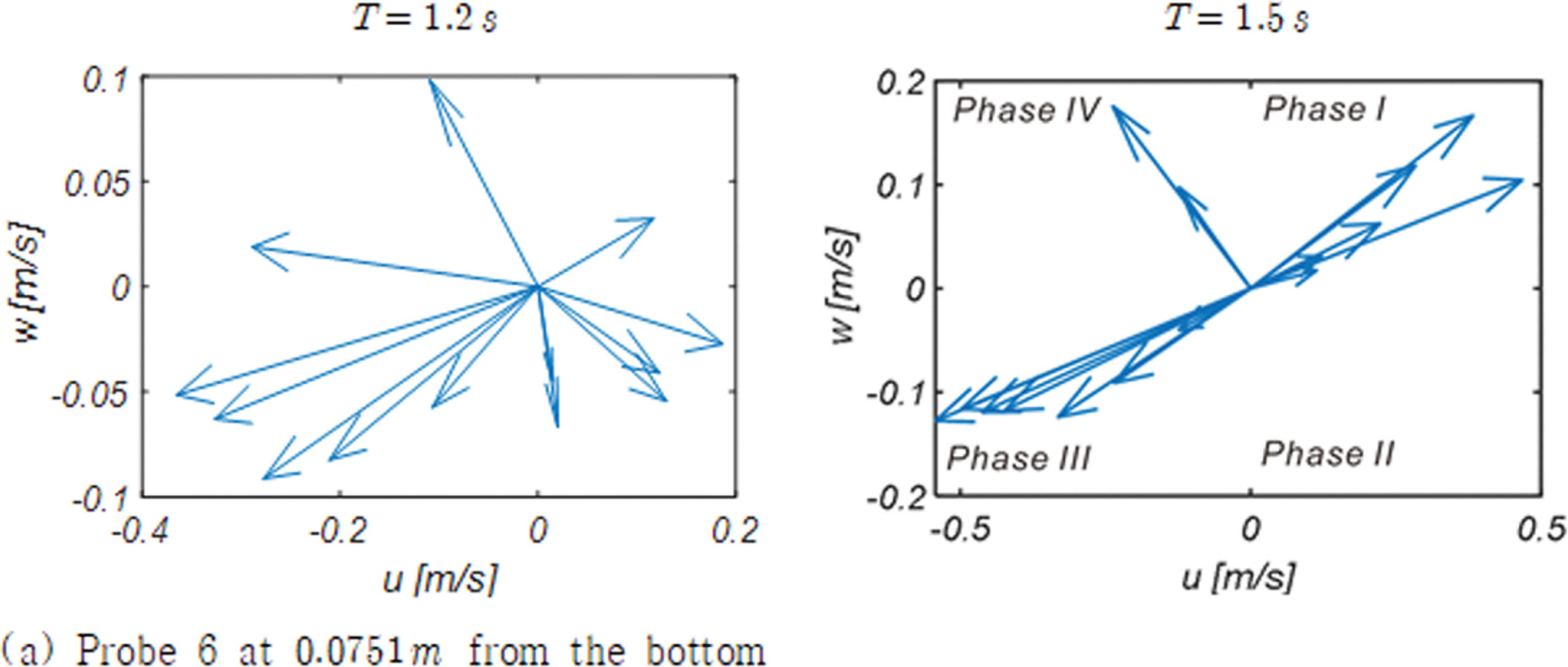
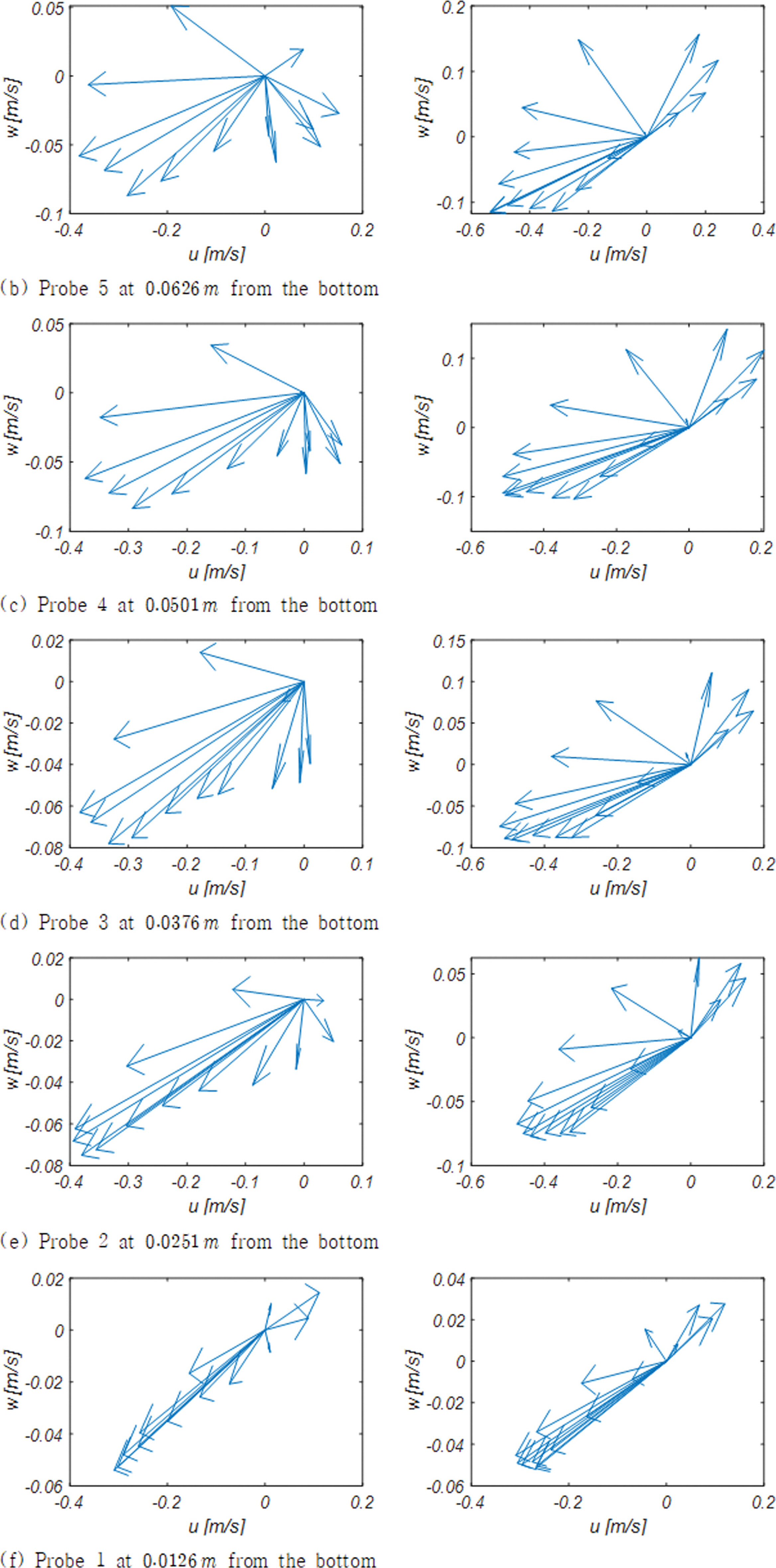
Fig. 11에는 단면 A - A'에 거치된 Wave Station 4(Fig. 5 참조)에서 바닥으로부터 각각 0.0126 m, 0.0251 m, 0.0376 m, 0.0501 m, 0.0626 m, 0.0751 m 떨어진 지점에서 유속 벡터가 [u, w]로 구성된 위상공간에서 하나의 주기에 걸쳐 그리는 궤적을 도시하였으며, RUN 1, 2에서 관측된 유속 벡터 궤적은 Appendix A에 수록하였다.

주기가 상대적으로 긴 RUN 4의 경우 선행 파랑에 의해 처올려진 해수에 의한 먼바다 방향의 회귀 류가 더해져 back wash의 세기는 RUN 3에 비해 많게는 세배 가까이 증가하는 것을 알 수 있다[Fig. 11(a) 참조].

또 한 후행 파랑의 선단부가 도착하는 경우 흐름 방향이 바닥이 거의 드러난 포 말대 방향으로 짧은 기간에 급격히 역전되는 것으로 보인다. 이러한 특성의 흐름은 온화한 해양환경에서 해빈이 복원되는 과정을 우리에게 시사하며 이 과정을 정리하면 다음과 같다: 너울로 구성된 파랑 무리에서 성분 파랑 간의 공진성 상호작용으로 생성된 외 중력파가 쇄파선 인근에 도달하는 경우 중력으로 인한 가속이 더해진 Phase II 파랑 궤도 운동으로 수면 가까이 상승한 많은 모래가 쇄파 시 발생하는 파 마루로부터 시작된 up-rush에 의해 전 빈 정점 가까이 이동하며 이 과정에서 발생하는 침투로 인해 퇴적되는 것으로 판단된다.

이에 비해 RUN 3의 경우 수면과 가까운 Probe 3, 4, 5, 6에서 전술한 변환은 점진적으로 진행되어 잘 갖추어진 파랑의 성정을 여전히 유지하고 있으나, 바닥과 가까운 Probe 1, 2에서는 해안공학계에 잘 알려진 대로 직선운동에 가까운 궤적을 그리는 것을 알 수 있다.

Fig. 12에는 수치 모의 된 유속으로부터(x = 13 m, 4 m < y < 14 m, z = 0.5 m)에서 추적을 시작한 유선을 도시하였으며, 사주 후면에 형성된 vortex tube가 잘 드러난 것으로 판단된다.

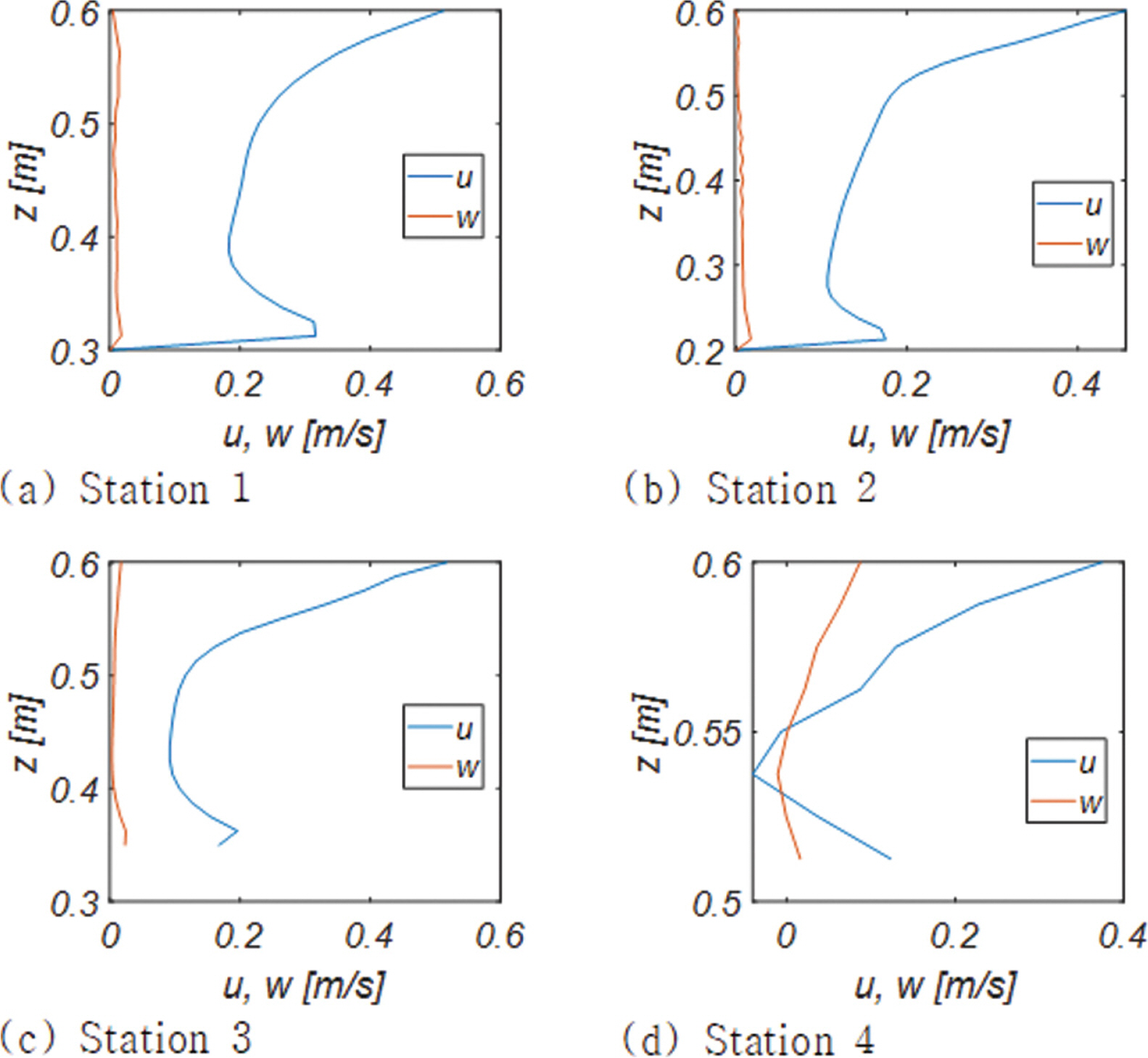
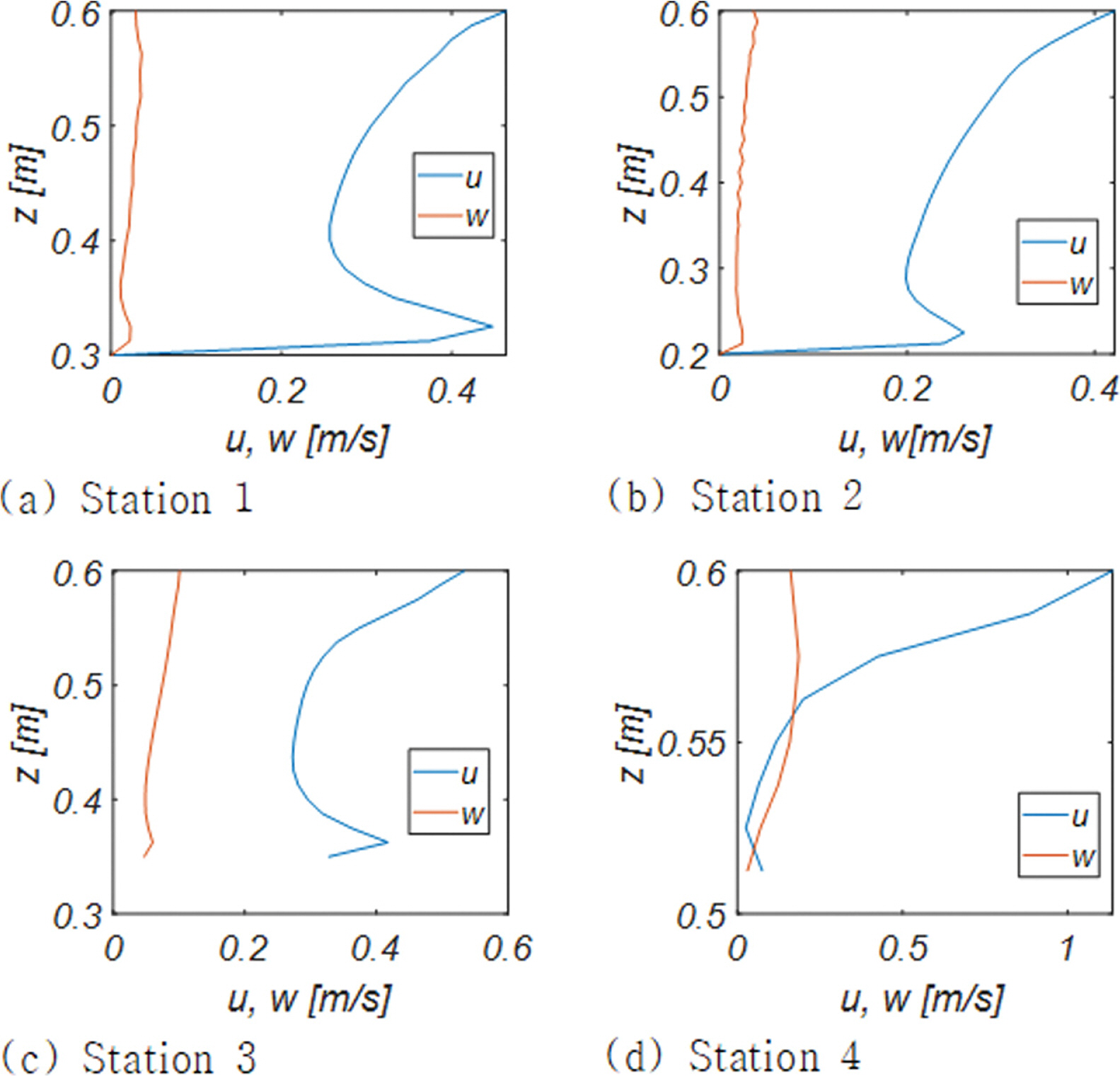
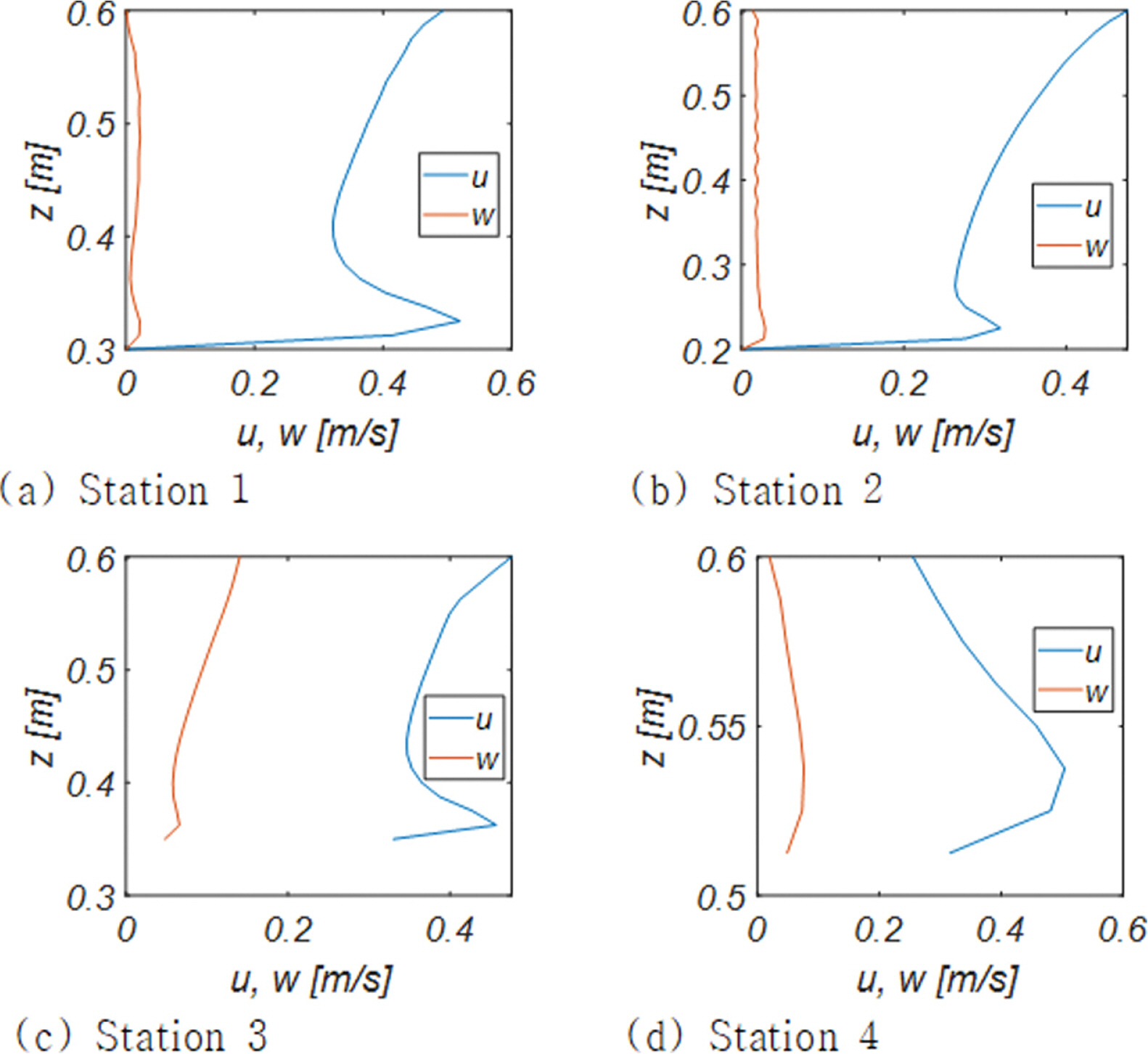
Fig. 13에는 RUN 1, 2, 3에서 관측된 단면 A - A'(Fig. 5 참조)에서의 경계층 streaming 진화과정을 도시하였으며 Fig. 14, 15, 16에는 이해를 돕기 위해 Wave Station 1, 2, 3, 4에서 관측되는 최대 해안 방향 유속 u_{B_MAX}과 u_{B_MAX} 발생 시 수직 방향 유속분포를 도시하였다.

Fig. 13, 14, 15, 16에서 알 수 있듯, 천수 과정의 각 단계에서 모두 경계층 streaming을 관측할 수 있으며, 최대 경계층 streaming은 사주 정점(Wave Station 1)에서 발생하며 주기가 가장 짧은 RUN 1의 경우 그 세기는 약 0.32 m/s 내외에 분포하였다. 이러한 수치는 free stream 유속 u_∞의 진폭(U_m = 0.18 m/s)의 두 배에 달하는 것으로 wave Reynolds 응력에 기반한 Longuet-Higgins(1957)의 해석 해(uBMAX = 0.0076 m/s)와는 상당한 차이를 보인다.

이해를 돕기 위해 경계층 streaming에 대한 Longuet-Higgins(1957)의 해석 해를 옮겨 적으면 다음과 같으며,

(14)

uBδ=fUm2c

여기서 uBδ는 경계층 상단 부(z = δ)에서의 경계층 streaming 세기, c는 파속, U_m는 경계층 상단에서의 첫 번째 성분 파랑에 기인한 유속진폭, δ는 경계층 두께를 각각 나타낸다. δ는 Stokes 길이로 불리기도 하며 다음과 같이 기술될 수 있다.

(15)

δ=2νω

식(14), (15)에서 ω는 파랑 각 주파수, f는 a/k_N에 종속하는 마찰 계수로 0.4 내외의 값을 지니는 것으로 전해지며, 여기서 a는 경계층 상단에서 파랑 내습 시 수입자가 그리는 궤적의 진폭으로 해안공학 계에서는 excursion amplitude로 불리며, k_N는 등가 Nikuradse roughness를 각각 나타낸다.

사주 저점에서 약 0.16m/s까지 감소 된 경계층 streaming은 이차 천수를 겪으면서 다시 0.2m/s까지 회복되나, 포말대(x = 15 m)에서는 다시 0.09m/s 내외로 감소하였다[Fig. 14(d) 참조].

이러한 현상은 전술한 x = 15 m는 선행 파랑에 의한 회귀류가 먼바다 방향으로 가속되는 구간으로 중간대역 0.5m< z < 0.56 m에서 관측되는 back-wash에 의해 감속되는 것으로 보인다.

Fig. 17에는 이해를 돕기 위해 Station 4에서 관측된 해안 방향 유속성분 연직 분포의 한 주기에 걸친 변화양상을 도시하였다. 한 주기를 총 여섯 개의 frame으로 나누어 위상별 유속 변화가 확연히 드러나도록 구성하였다. 그림에서 알 수 있듯 swash-zone에 해당하는 Station 4의 경우 전 수심이 경계층으로 보이며 바닥 인근으로 경계층을 제한하는 고전적인 해석방법은 한계가 있어 보인다.

5. 결론

자연 해빈은 해양환경에 따라 침·퇴적을 반복하며 고 파랑에 의해 해빈이 대규모로 침식되더라도 폭풍이 잦아들고 너울이 우세한 해양환경이 회복되는 경우 점진적으로 복원되며, 이러한 해빈 복원은 경계층 streaming을 통해 이루어진다(Cho and Kim, 2019; Cho et al., 2019; Cho, 2019a). 전술한 해빈 대순환과정 중 온화한 해양환경에서 출현하는 퇴적 성 해빈은 Dean Number Ω <1로 분류되며 좁은 해빈 폭, 급한 전빈 경사, swash 대역에서 형성되는 beach cusp, 원 빈에 형성된 사주 등의 성정을 지닌다. 이에 반해 거친 해양환경에서 출현하는 침식성 해빈은 고운 모래로 구성된 해빈, 완만한 전빈 경사, 쓸려간 사주와 같은 성정을 공유한다. 이처럼 beach cusp은 해빈 복원과정을 구성하는 중요한 요소라는 점에서 beach cusp을 포함한 swash zone에서의 경계층 streaming 수리특성을 살펴보는 작업은 상당한 공학적 가치를 지니며, 해빈 침식 대응방안 최적화 과정에서도 적지 않은 역할을 담당할 수 있을 것으로 판단된다(Cho, 2019b).

이러한 시각에서 본 논문에서는 너울이 우세한 온화한 해양환경에서 출현하는 beach cusp에서의 경계층 streaming 수리특성을 살펴보기 위해 edge waves 천수 과정을 수치 모의하였으며 beach cusp의 진폭 A_B과 파장 L_B은 맹방 해변에서 수행된 관측결과(Cho, 2019b)를 토대로 각각 1.25 m, 18 m로 선정하였다. Beach cusp을 유지하는 것으로 알려진 synchronous edge waves는 같은 주기와 파고를 지니는 두 개의 Cnoidal wave가 전면해역에서 비스듬히 조우 되도록 조파하여 재현하였으며 이 경우 결과되는 파동 계는 연안 방향으로 파고가 변조되는 short-crested waves로 synchronous edge waves와 같은 성정을 지닌다. 비교를 위해 영의 영각으로 진입하는 Cnoidal waves의 천수 과정 수치 모의도 병행하여 수행하였다. 수치 모의는 OpenFoam 기반 Tool box인 IHFoam을 사용하여 수행되었으며(Losada et al., 2008; Cho and Bae, 2019). 파랑모형은 spatially filtered Navier-Stokes Eq.과 질량 보존식으로 구성하였다. 자유수면은 VOF(Volume Of Fraction)법을 활용하여 추적하였으며, 난류모형으로는 차용된 격자보다 작은 규모의 난류는 등방성에 근접한다는 시각에서 LES(Large Eddy Simulation), 잔차 응력(residual stress)은 one equation dynamic Smagorinsky 모형을 활용하여 모의하였다.

모의결과 천수 과정의 각 단계에서 예외 없이 경계층 streaming을 관측할 수 있었으며, 최대 경계층 streaming은 사주 정점에서 발생하였으며 주기가 가장 짧은 RUN 1의 경우 그 세기는 약 0.32 m/s 내외에 분포하였다. 이러한 수치는 free stream 유속 u_∞ 진폭(U_m = 0.18 m/s)의 두 배에 달하는 것으로 wave Reynolds 응력에 기반한 Longuet-Higgins(1957)의 해석 해(uBδ = 0.0076 m/s)와는 상당한 차이를 보인다. 수치 모의과정에서 온화한 해양환경에서 해빈이 복원되는 과정을 특정할 수 있었으며 이 과정을 정리하면 다음과 같다: 너울파 군에서 성분 파랑 간의 공진성 상호작용(resonance wavewave interaction)으로 생성된 장주기의 외 중력파가 쇄파 되는 경우 전술한 파랑의 궤도 운동으로 수면 가까이 상승한 모래는 파 마루로부터 시작된 up-rush에 의해 전 빈 정점 가까이 이동하여 퇴적하는 것으로 추정된다. 또 한 swash-zone의 경우 경계층은 전 수심으로 구성되며, 바닥 인근으로 경계층을 제한하는 고전적인 해석방법을 swash-zone으로 확대 적용하는 경우 상당한 오류를 초래할 수 있는 것으로 모의 되었다.

감사의 글

본 연구는 해양수산부의 “연안 침식 저감기술 개발” 성과 중 일부로, 지원에 감사드립니다.

Fig. 1.

Schematic sketch of two dominating mechanism-boundary layer streaming and under tow- on the cross shore sediment transport under low waves and high waves [from Chang and Cho (2019)].

Fig. 2.

Layout of the Mang-Bang beach and its beach cusps, measured beach profiles across the shore of Mang-Bang.

Fig. 3.

A diagram in wave number, frequency space illustrating the four components that satisfy the quartet resonance condition where the dispersion relation, ω=±gh, is represented by trumpet shaped surface in three-dimensional spaces following Phillips (1977).

Fig. 4.

Definition sketch of synchronous edge waves, which would sustain the beach cusps formed along the shore-line [modified from Cho (2019)].

Fig. 5.

Schematic sketch of numerical basin.

Fig. 6.

Bird-eye plot of the numerical basin and its corresponding mesh used for the numerical simulation.

Fig. 7.

Sequential snapshots of numerically simulated free water surface when the short-crested waves formed by two obliquely colliding Cnoidal waves of T = 3.0 s are shoaling over the beach cusp.

Fig. 8.

Sequential vector plots of numerically simulated velocity field when short-crested waves formed by two obliquely colliding Cnoidal waves are shoaling toward the beach cusp.

Fig. 9.

Sequential vector plots of numerically simulated velocity field across the section A – A’ when short-crested waves formed by two obliquely colliding Cnoidal waves are shoaling toward the beach cusp for T = 1.8 s.

Fig. 10.

Fig. 11.

Evolution of velocity vector during the unit wave period at the varying height for T = 1.8 s and T = 3.0 s (Wave Station 4).

Fig. 12.

Vortex tube in the wake of a sand bar detected by stream-lines.

Fig. 13.

Evolution of boundary layer streaming across the shore when the short-crested waves formed by two obliquely colliding Cnoidal waves of varying period are shoaling over the beach cusp.

Fig. 14.

Comparison of boundary layer streaming and vertical velocities at the varying stages of shoaling process for T = 1.2 s.

Fig. 15.

Comparison of boundary layer streaming and vertical velocities at the varying stages of shoaling process for T = 1.5 s.

Fig. 16.

Comparison of boundary layer streaming and vertical velocities at the varying stages of shoaling process for T = 1.8 s.

Fig. 17.

Evolution of shoreward velocity during unit wave period at wave station 4 for T = 1.2 s, T = 1.5 s, and T = 1.8 s.

Table 1.

List of wave conditions used in the numerical simulations

Cases	H [m]	T [s]	Wave type
RUN 1	0.15	1.2	Two colliding Cnoidal Waves
RUN 2	0.15	1.5	Two colliding Cnoidal Waves
RUN 3	0.15	1.8	Two colliding Cnoidal Waves
RUN 4	0.15	3.0	Two colliding Cnoidal Waves
RUN 5	0.20	1.5	Normally attacking Cnoidal Waves
RUN 6	0.15	1.8	Normally attacking Cnoidal Waves

References

Chang, PS, Cho, YJ. (2019). Preliminary study on the development of a platform for the optimization of beach stabilization measures against beach erosion III - centering on the effects of random Waves occurring during the unit observation period, and infra-gravity waves of bound mode, and boundary layer streaming on the sediment transport, Journal of Korean Society of Coastal and Ocean Engineers, 31(6):434-449 (in Korean)..

Cho, YJ. (2019a). Numerical analysis of the beach stabilization effect of an asymmetric ripple mat, Journal of Korean Society of Coastal and Ocean Engineers, 31(4):209-220 (in Korean)..

Cho, YJ. (2019b). Grand circulation process of beach cusp and its seasonal variation at the Mang-Bang beach from the perspective of trapped mode Edge waves as the driving mechanism of beach cusp formation, Journal of Korean Society of Coastal and Ocean Engineers, 31(5):265-277 (in Korean)..

Cho, YJ. (2019c). Preliminary study on the development of a platform for the optimization of beach stabilization measures against beach erosion II - centering on the development of physics-based morphology model for the estimation of an erosion rate of nourished beach, Journal of Korean Society of Coastal and Ocean Engineers, 31(5):320-333 (in Korean)..

Cho, YJ, Bae, JH. (On the feasibility of freak waves formation within the harbor due to the presence of Infra-gravity waves of bound mode underlying the ever-present swells, Journal of Korean Society of Coastal and Ocean Engineers, 2019). 31(1):17-27 (in Korean)..

Cho, YJ, Kim, GS. (2008). Development of 3-D nonlinear wave driver using SPH, Journal of the Korean Society of Civil Engineers B, 28(5B):559-573 (in Korean)..

Cho, YJ, Kim, GS, Ryu, HS. (2008). Suspension of sediment over swash zone, Journal of the Korean Society of Civil Engineers B, 28(1B):95-109 (in Korean)..

Cho, YJ, Kim, IH. (2019). Preliminary study on the development of platform for the selection of an optimal beach stabilization measures against the beach erosion-centering on the yearly sediment budget of the Mang-Bang beach, Journal of Korean Society of Coastal and Ocean Engineers, 31(1):28-39 (in Korean)..

Cho, YJ, Kim, IH, Cho, YJ. (2019). Numerical analysis of the grand circulation process of Mang-Bang beach-centered on the shoreline change from 2017. 4. 26 to 2018. 4. 20, Journal of Korean Society of Coastal and Ocean Engineers, 31(3):101-114 (in Korean)..

Cho, YJ, Lee, H. (2007). Numerical analysis of nonlinear shoaling characteristics over surf zone using SPH and lagrangian dynamic smagorinsky model, Journal of Korean Society of Coastal and Ocean Engineers, 19(1):81-96 (in Korean)..

Eckart, C. (1951). Surface waves on water of variable depth, Wave Report 100, University of California, Scripps Institution of Oceanography, Wave Report, 100, SIO Ref No 51–12.

Guza, RT. (1974). Excitation of edge waves and their role in the formation of beach cusps. University of California, San diego, Ph.D., p 1974 Oceanography..

Hasselmann, K. (1967). A criterion for nonlinear wave stability, Journal of Fluid Mechanics, 30(4):737-739.

Lee, HJ, Cho, YJ. (2019). Numerical analysis of synchronous Edge wave known as the driving mechanism of beach cusp Journal of Korean Society of Coastal and Ocean Engineers, 31(6):409-422 (in Korean)..

Longuet-Higgins, MS. (1957). The mechanics of the boundary layer near the bottom in a progressive wave, Proc. 6th International Conference on Coastal Engineering, Gainesville, Palm Beach and Miami Beach. Florida: December). 184-193.

Losada, IJ, Gonzalez-Ondina, JM, Diaz, G, Gonzalez, EM. (2008). Numerical simulation of transient nonlinear response of semi-enclosed water bodies: model description and experimental validation, Coastal Engineering, 55(1):21-34.

Meneveau, C, Lund, TS, Cabot, WH. (1996). A Lagrangian dynamic sub-gird scale model of turbulence, Journal of Fluid Mechanics, 319, 353-385.

Phillips, OM. (1980). The Dynamics of the Upper Ocean. 2nd edition. Cambridge: Cambridge University Press.

Pope, SB. (2004). Ten equations concerning the large-eddy simulation of turbulent flows, New Journal of Physics, 6(35):1-24.

Smagorinsky, J. (1963). General circulation experiments with the primitive equations, Monthly Weather Rev NWB, 91(3):99-164.

Yoshizawa, A, Horiuti, K. (1985). A statistically-derived subgrid-scale kinetic energy model for the large-eddy simulation of turbulent flows, Journal of the Physical Society of Japan, 54(8):2834-2839.

APPENDICES

Appendix A

Fig. A1.

Sequential snapshots of numerically simulated free water surface when normally attacking single Cnoidal waves of T = 2.4 s are shoaling over the beach cusp.

Fig. A2.

Evolution of velocity vector during the unit wave period at the varying height for T = 1.2 s and T = 1.5 s (Wave Station 4).