1. 서 론
연안 모델의 예측 정확성을 향상시키기 위해서는 광역 모델로부터 신뢰할 수 있는 경계조건과 초기조건을 전달받아야 하며 이를 위해 다양한 해양수치모델 연구들이 한반도를 중심으로 진행되어 왔다(Kang et al., 1991; Kim and Kim, 1999; Teague et al., 2000; Lee et al., 2003; Chang et al., 2014). 하지만 광역 모델 기반의 연구들은 연안역에서 조석 재현 및 검증하기 위한 해상도가 상대적으로 낮고 고해상도 전환에 따른 높은 계산비용으로 인해 예측 한계성을 지닌다. 조석의 경우 조위 검조소의 위치는 섬을 제외한 연안역에 위치해 있으며 광역 모델의 조석전파가 연안까지 도달하면서 축소됨에 따라 연안역을 저해상도로 구성할 경우 정확성에 대한 한계점이 남아있다.
자료동화는 활용 가능한 모든 정보를 사용하여 정확도가 가장 높은 초기장으로 정의하기도 하며(Talagrand, 1997), 수치모델의 적분과정에서 초기 자료를 이용하여 다음 시간의 영역에 내삽하는 방법을 의미하기도 한다(Bennett, 2002). 이렇게 다양한 해석을 할 수 있는 자료동화의 정의에서 하나의 공통점이 있다. 그것은 관측자료를 수치모델에 반영하여 기존 수치모델의 한계점을 개선시킬 수 있는 방법론이라는 점이다.
해양 수치모델의 예측 정확성을 향상시키기 위한 자료동화 연구는 광역 모델 기반의 위성자료를 중심으로 SST(Sea Surface Temperature) 자료동화 연구가 활성화되어 있다(Weare et al., 1976; Høyer and She, 2007; Reynolds and Smith, 2009; Xu and Shen, 2013). 허나 연안 중심의 연속관측자료를 활용한 자료동화 연구 사례는 국외 연구사례로 Kruapov(2005)가 ADCP을 활용하여 연안에 수층별 유속자료를 적용한 연구가 있으나 국내의 경우에는 해당 관측자료 수집이 현실적으로 어렵기 때문에 유사 사례 연구를 찾기 힘들다.
북위 32.123도 동경 125.182도에 위치한 이어도 종합 과학기지는 한반도 해역 최초의 외해에 위치한 무인관측기지이다. 이어도 종합 과학기지에서는 쿠로시오 해류로부터 이어져 오는 황해난류와 쓰시마 난류의 기점 부근에 위치해 있어 한반도로 접근해오는 태풍의 진입경로와 접근시간을 추정하는데 유용한 해양정보를 제공한다. 또한 한반도 내륙에서 가장 멀리 떨어진 영역에서 관측되는 해양정보를 바탕으로 연안모델에 필요한 경계조건 수립에 많은 도움이 될 것으로 기대하고 있다.
본 연구는 이어도 종합 과학기지에서 제공된 연안 관측자료를 기반으로 광역 모델의 자료동화를 서남해안 연안까지 확장하고 기존 관측자료와의 자료동화연계를 통한 해양수치모델의 정확성 개선을 도모하고자 한다. 그러기 위해 서남해안을 중심으로 수층별 유속관측자료를 활용하여 해양순환모델에 최적내삽법을 적용할 경우 요구되는 최적매개변수를 산정하였다. 자료동화 적용시 배경 모델은 복잡한 해안성을 포함하는 한반도해역에 적합한 비구조격자체계의 해양순환모델을 기반한다. 적용된 해양 자료동화기법은 최적내삽법을 이용하였고 이어도 과학기지를 포함하는 서남해역의 정점별 ADCP 유속자료를 활용하였다. 자료동화를 적용하기에 앞서 요구되는 매개변수들의 최적값을 산정하기 위하여 각 실험별 결과들을 Taylor diagram을 사용하여 최적조건을 산출하고 이를 바탕으로 서남해안에서의 유속자료를 최적내삽법으로 적용할 경우 요구되는 매개변수의 의미와 향후 해양자료동화의 연구개발 방향성을 제시한다.
2. 연구 개요
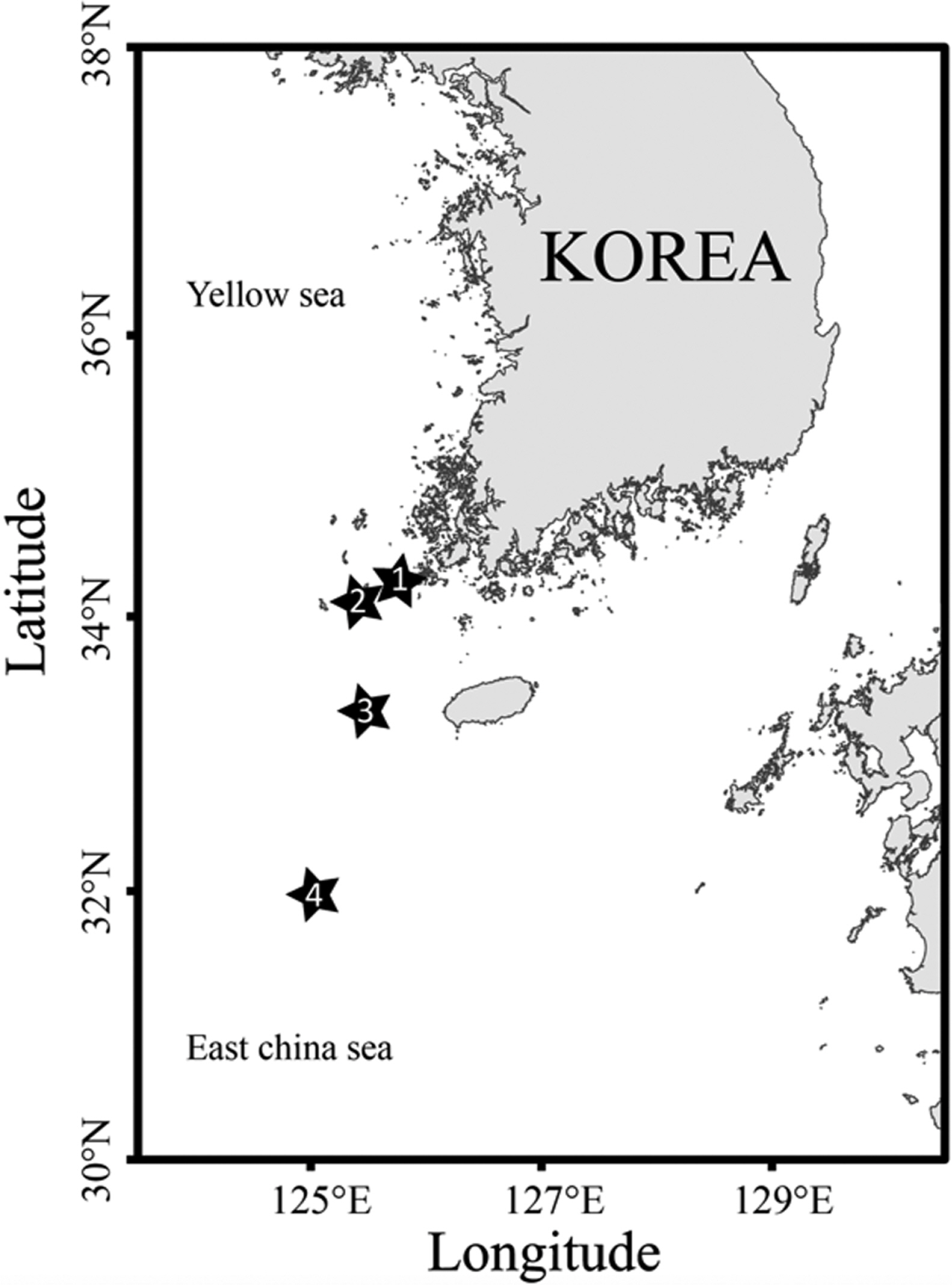
연구 대상은 Fig. 1에서 알 수 있듯이 이어도 과학 기지를 포함하여 서남해역과 동중국해 일부을 포함하는 한반도 중심으로 설정하였다. 자료동화를 적용하기 위해서는 3가지 요소가 필요하다. 첫 번째는 시스템이라 일컫는 배경 모델이 필요하며 배경 모델로부터 배경 오차 공분산이 산정된다. 두 번째는 자료동화에 필요한 관측 자료이며 자료동화 적용전에 관측 오차가 관측 시행자의 분석에 의해 선정되어야 한다. 마지막으로는 자료동화 기법을 선정해야 한다. 계산 비용과 추정값에 대한 반응이 연구 목적에 적합한 자료동화 기법을 선정해야한다.
2.1 관측자료 - 수층별 유속자료
해양자료동화를 적용하기 위해 사용된 수층별 유속자료는 국립해양조사원에서 관측시행하여 얻는 자료를 사용하였다. 관측에 사용된 장비는 ADCP를 사용했으며 이는 도플러효과를 이용하여 유속 수직 단면관측이 가능하다. 본 연구에 Fig. 1처럼 이어도 종합 과학기지를 포함하여 서남해역에 3곳의 추가 정점에서의 수층별 유속자료를 활용하였고 관측정점별로 시간 및 관측간격, 좌표 등 의 정보는 Table 1에 정리하였다.
이어도 과학 기지 자료는 국립해양조사원으로부터 정보 제공 동의를 받아 사용하였으며 해당 자료는 2006년 자료에 해당된다. 이어도 과학 기지의 관측자료를 제외한 나머지 3정점의 자료 기간은 각각 상이하며 이는 향후 조화분해를 통해 다시 동일 기간 자료로 재생성하여 자료동화에 사용되었다. 특히 이어도 과학기지의 위치는 쿠로시오 해류와 쓰시마 난류의 영향을 받는 해역으로써 그 영향을 고려해야 하지만 본 연구에서는 광역 모델의 조석 전파를 중점적으로 보기 때문에 조석류 외의 영향 성분을 제한하고 접근하였다.
2.2 배경 모델
Chen et al.(2003)에 의해 개발된 FVCOM 은 연안모델에 적합한 비구조격자체계의 3차원 해양 순환 수치모델이다. FVCOM이 갖고 있는 주요 장점은 유한체적법과 비구조격자체계, 병렬화기법이다. 기존의 유한차분법이 갖는 수직적분의 빠른 차분화기법과 유한요소법의 기하학적 장점을 차분형태가 아닌 적분형태로 병렬화하기 때문에 정확성과 계산효율이 효과적이다.
관측자료가 위치한 서남해안에서는 동해와 외해에 비해 상대적으로 수심이 매우 낮고 복잡한 해안선을 가지고 있기 때문에 조석의 영향이 지배적이고 이로 인해 조수간만의 차가 크다. 본 연구에서는 유속 자료의 조석성분만을 고려하여 관측자료를 재구성한 뒤 자료동화하였고 요구되는 매개변수의 최적값을 찾기 위한 배경 모델은 조석만 외력조건으로 구성하였다. 조화상수중에서 서남해안에서 영향력이 가장 높은 반일주조 성분 M2 만 사용하여 실험 목적에 적합하게 구성하였다. 조화상수값은 NAO.99Jb(Matsumoto et al., 2000) 로부터 얻은 조화상수값을 개방경계 절점에 내삽한 뒤 배경 모델 입력자료 형태로 변환하여 모델 내에 반영하였다.
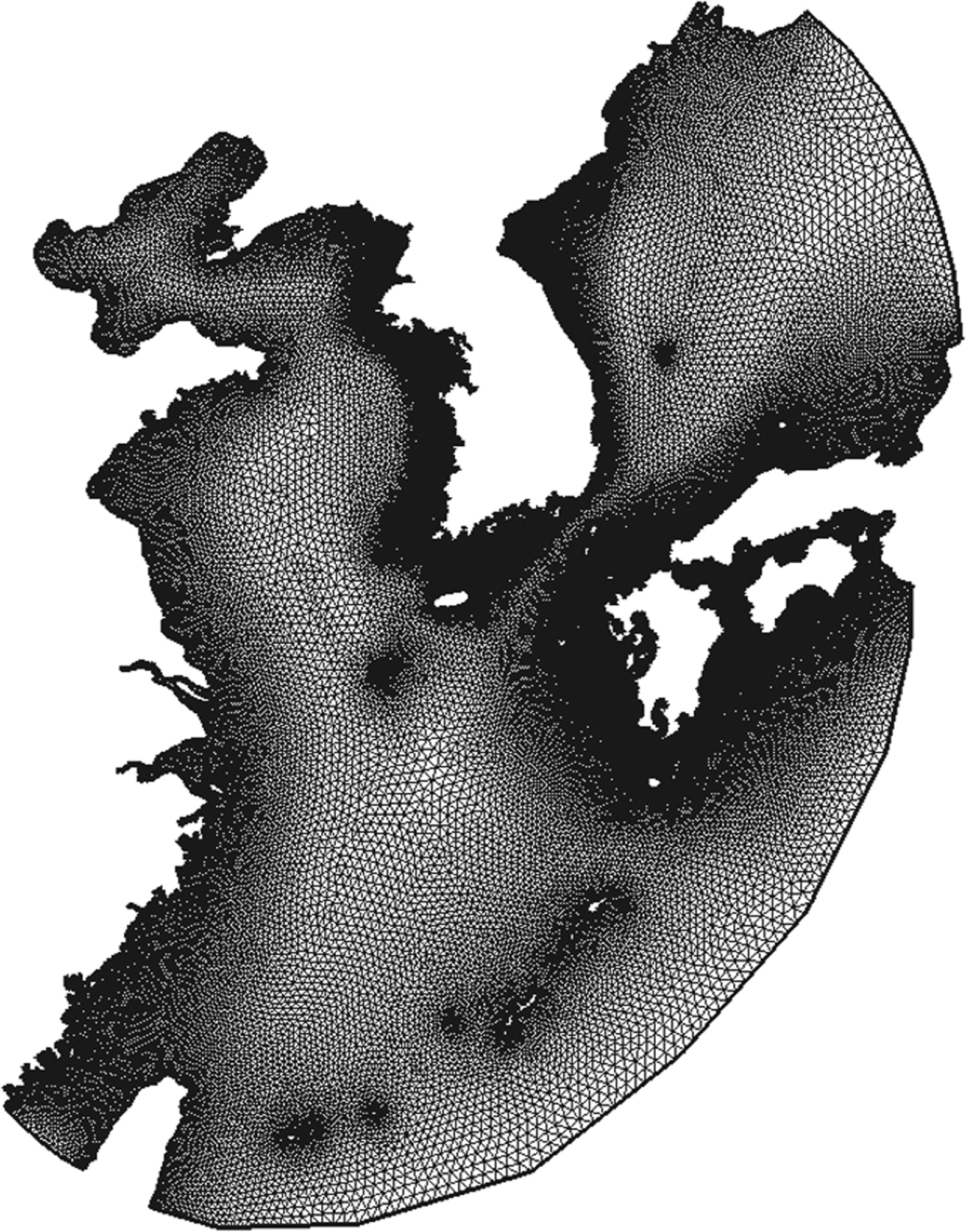
배경 모델의 전체 영역은 Fig. 2와 같이 한반도를 중심으로 구성하였다. 동중국해와 동해에서 조간대 및 연안역을 진입을 할 때 극심한 수심변화를 나타나게 되는데 이 때 발생되는 수치모델의 불안정을 방지하기 위하여 격자해상도를 연안으로 진입할 수록 부드럽게 재구성하였다. 배경 모델 격자의 해상도 범위는 0.12~30 km이고 모델 영역을 구성하는 절점수와 요소수는 각각 49,244개와 93,727개이다. 모델 영역 내의 수심구성은 Seo(2008)가 개발한 한국 주변해역 30초 격자수심(KorBathy30s)을 사용하였으며 수심의 범위는 조간대를 포함하여 -5.0~7237 m이다. 초기 구성된 배경 모델은 안정화 시간 5일을 포함하여 총 35일을 모의했으며 CFL(Courant-Friedrich Levy) 조건을 고려하여 계산시간은 5초 단위로 설정하였다. 연직수층의 경우에는 σ-좌표계를 활용하여 10개의 Sigma-layer로 균등하게 적용하였다.
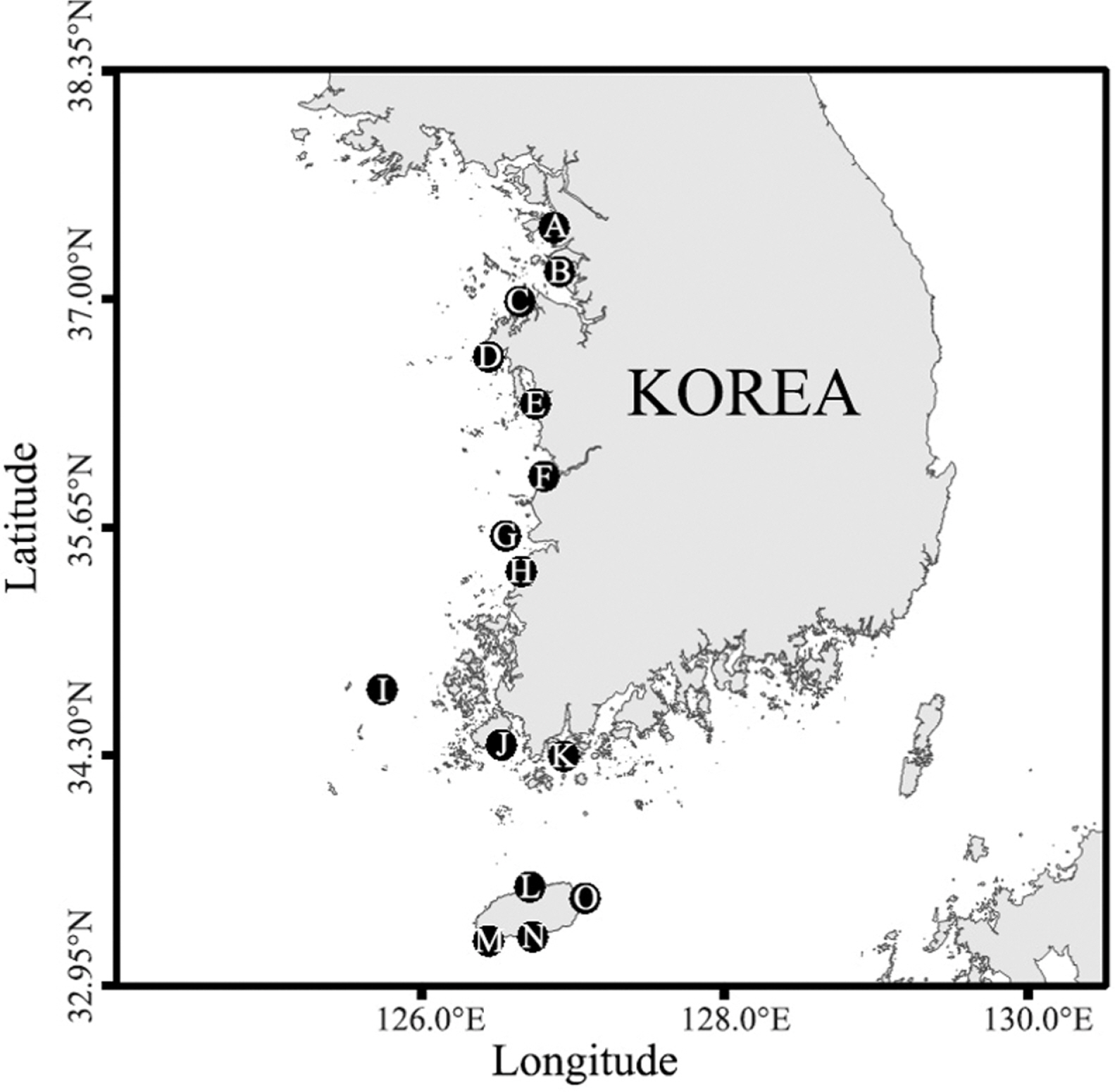
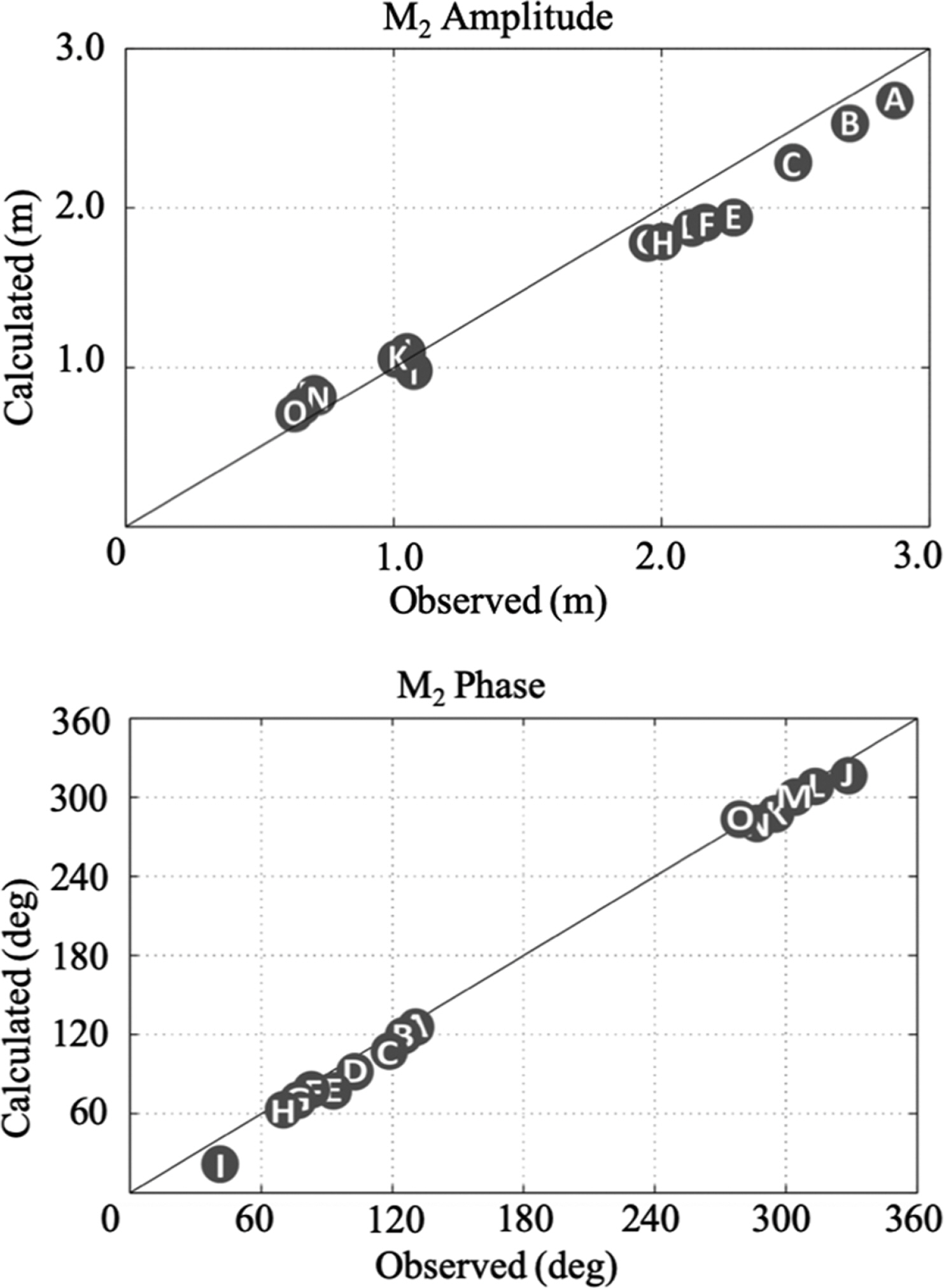
자료동화 적용하기 전 배경 모델의 신뢰성을 검증하기 위해 서남해안에 위치한 조위관측소(Fig. 3)의 조위자료를 활용하여 조석검증하였다. 총 15개의 조위관측소별로 얻은 조위자료에서 조화분해분석을 통하여 M2에 대한 조화상수를 추출하고 모델 계산 결과에서도 동일한 위치에서의 조위시계열에서 같은 조화분해방법을 통해 M2에 대한 조화상수를 추출하여 비교하였다. Fig. 4에서 알 수 있듯이 조위관측소의 자료와 수치모의한 모델의 결과값이 1:1 상응했을 때 수치모델은 90% 이상 대상해역을 재현했다고 할 수 있다.
정략적인 오차분석을 통해 과학적으로 모델을 검증하고자 평균 제곱근 오차(Root Mean Square Error; RMSE)을 계산하였다. 평균 제곱근 오차는 정량적으로 관측값와 배경값 사이의 오차를 표시하는데 특히 제곱근방식을 사용함에 따라 오차의 편차가 커질수록 그 값들이 커진다는 특징이 있다. 본 연구에 활용된 배경모델의 M2 진폭의 평균 제곱근 오차는 0.05 m이고 위상은 0.86도이다. 결과적으로 구축한 해양순환 수치모델의 조석결과는 관측값과 10% 내외의 오차율을 보여주고 있다.
2.3 자료동화 기법 - 최적내삽법
자료동화 과정에서 추정값(Xanalysis)은 식(1)과 같이 관측값(Yobservation)과 배경값(Xbackground)을 기반으로 계산된다.
여기서 H는 관측값(Yobservation)의 위치 정보를 갖고 있는 행렬인 Measurement function이다. [Yobservation H(Xbackground)] 을 일컫는 Innovation은 배경값에서 H와 행렬곱을 통해 관측값의 위치에 있는 배경값을 구하고 이를 관측값과의 오차로 표현한다. 이러한 Innovation과 곱해지는 Wtotal는 Total weight function으로써 0부터 1 사이의 값을 가지는 무차원수이다. 이는 자료동화에서 관측값과 배경값의 상관관계를 결정짓는 중요한 요소로 작용하는데, Wtotal = 1일 경우에는 관측값을 100% 신뢰하겠다는 의미를 가지는 반면 Wtotal = 0일 경우에는 관측값을 신뢰할 수 없고 오직 배경값에만 의존한다는 것을 의미한다. 일반적으로 Wtotal는 관측오차공분산과 배경오차공분산의 상관관계를 통해서 산정되고 관측오차공분산이 클수록 Wtotal는 감소하고 이는 관측값의 신뢰도가 낮아지는 것을 나타낸다.
본 연구에서 적용된 OI에서는 Cressman(1959) 가 개발한 Cressman analysis와 연계한다. 식(2)와 같이 Cressman analysis의 추정값은 앞서 설명한 일반적인 추정값 계산방식과 동일하나 Cressman weight라 불리는 Weight function에서 차이를 둔다. 이는 Kalman filter에서 사용되는 Gain matrix와 의미가 같으며 Innovation과 행렬곱을 계산하기전에 관측값과 모델값의 단순한 시·공간상의 거리비를 기준으로 산정되고 이 값을 최종적으로 Gain matrix의 벡터곱으로 자료동화보정값을 산정한다. 이러한 Cressman weight는 OI보다 쉽고 간단한 Nudging에서 찾아 볼 수 있다.
여기서 α0는 관측값을 나타내고 αp는 i번째 관측정점에서의 배경값을 나타낸다. F(a, x, y, z, t)는 시간 t 그리고 x, y, z 공간상에서 위치한 배경값을 의미하고 Gα는 본 연구에서 산정하고자 하는 매개변수 Scaling factor를 의미한다. Scaling factor란 일반적으로 연변화나 계절변화와 같은 주기변화가 긴 상태에서 순간적인 오차분산을 나타내기 어려울 때 사용된다. 따라서 Cressman analysis에서 Scaling factor의 값의 차이가 자료동화의 효율과 성능을 나타내는데 영향을 미친다.
본 연구에 Scale factor 외에 산정하는 다른 자료동화 매개변수는 Correlation length이며 이는 Cressman analysis에서 사용되는 Total weight function에서 사용된다. Total weight function 인 Wi는 식(3)과 같이 표현되며 각 성분은 식(4)~(7)과 같이 표현된다.
여기서 Wi는 관측정점에서 관측값과 임의의 모델 절점에서 계산된 배경값 사이의 시공간적인 비중을 모두 곱한 값으로 사용된다. 여기서 Wxy는 수평공간에서의 관측정점과 모델 계산절점간의 수평 사이거리를 비율로 환산하여 결정한다. Wσ는 수직공간에서의 비중을 뜻하고 Wθ는 관측정점과 배경절점 사이의 기울기를 의미하며 Wt는 관측시간에 대한 현재 모의시간의 비중을 의미한다.
특히 Wxy과 Wσ에서는 Correlation length(R)가 사용되는데 계산절점이 관측정점과 사이거리인 r이 0에 가까울 수록 Wxy는 1에 수렴하고 r이 R을 넘는 모든 계산 절점에선 Wxy = 0이 됨으로써 Wi = 0이 된다. Wσ도 마찬가지로 수직방향으로 R의 범위내에서 Wσ를 산정하는데, FVCOM의 경우에는 수직좌표체계를 σ-좌표계를 사용하기 때문에 SI단위을 σ 단위로 환산한 Rσ로 수직방향의 Weight을 결정한다.
일반적으로 Correlation length는 해당 관측정점에서 관측값이 주변에 영향을 미칠수 있는 범위를 나타낸다. 이는 계산절점으로부터 자료동화 계산 모듈이 미치는 영향거리를 의미하며 계산절점과 거리가 가까울수록 관측자료의 의존성이 높아지고 멀리 떨어질수록 배경 모델의 의존성이 높아지게 된다. 이것이 보여주는 의미는 실질적으로 해당 관측정점의 지형적, 물리적 특성이 공간적으로 영향을 미치도록 설정하는 것이며 경험적 연구를 통해 산정되는 매개변수이다.
3. 자료동화 적용 및 연구 방법
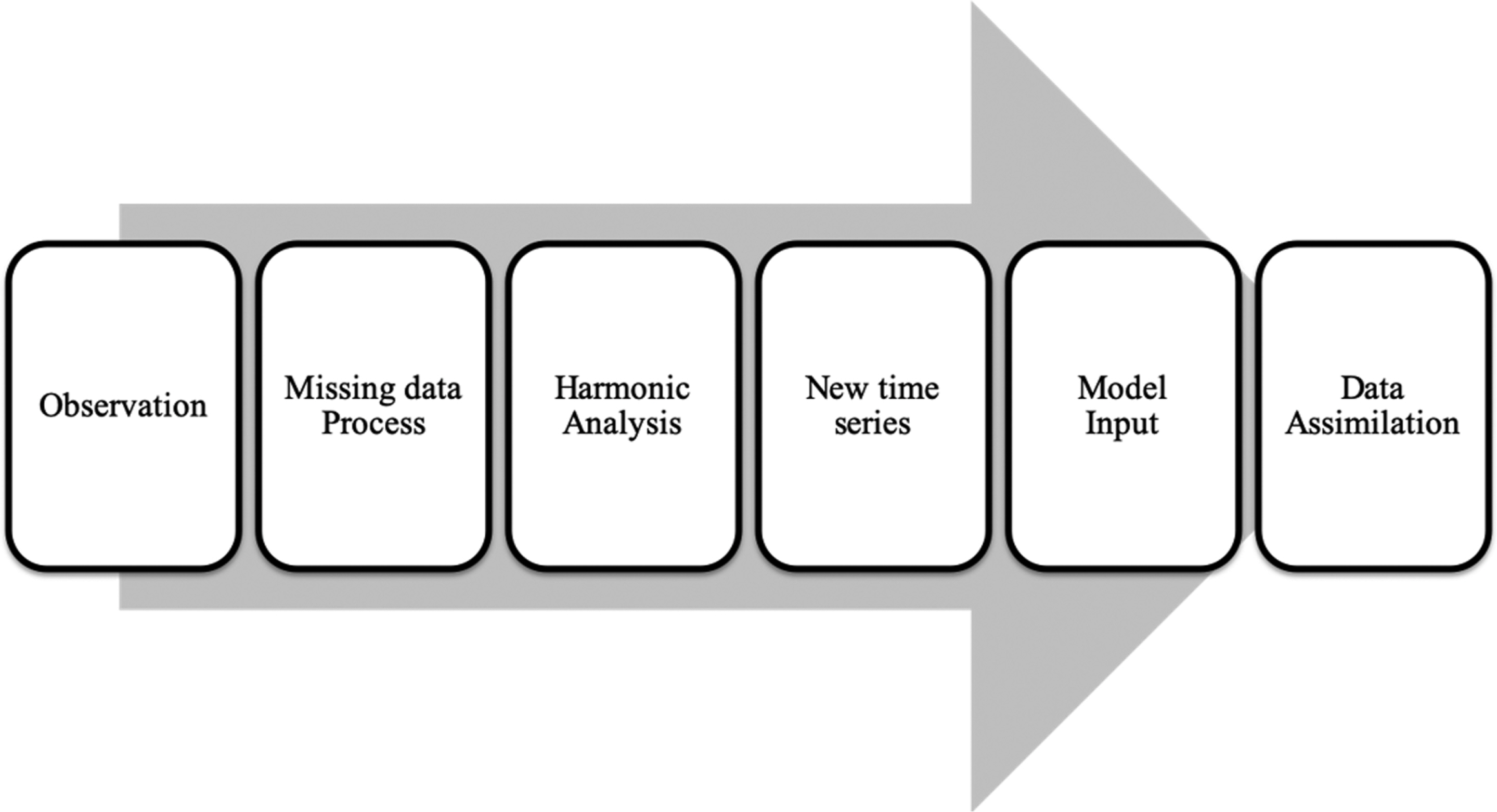
본 연구에 활용된 유속 관측 자료들은 관측된 시기가 서로 상이하다. 동시에 외해역과 연안역에서의 장기 연속 관측을 시행하기에 요구되는 관측비용과 분석 시간이 현실적으로 어렵기 때문이다. 따라서 본 연구의 목적에 맞게 각 관측 정점에서의 장기 유속 시계열 자료를 조화분해 한 후, 다시 모의시간에 맞게 입력자료를 재생성하였다. 본 과정을 단계별로 설명하자면 Fig. 5과 같이 정리할 수 있는데 먼저 원시자료로부터 결측구간을 보정한 뒤 시계열자료를 생성하고 조화분해를 한다. 조화분해하여 얻은 조화상수값들을 바탕으로 모의기간동안의 시계열자료를 재생성한 다음에 이를 바탕으로 모델 입력 자료로 구성한다. 조화분해 후 시계열 자료를 재생성하는데 사용된 도구로는 T_Tide Harmonic Analysis Toolbox(Pawlowicz et al., 2002)을 활용했다.
본 연구에서 선정할 매개변수의 최적값은 관측자료의 위치에 따라 물리적, 지형적 요인 등의 다양한 이유로 요구되는 값이 상이하다. 현재까지 서남해안 내에 관측 정점별로 명확한 매개변수의 최적값이 제시되지 않고 있으며 이는 경험적 산정을 통해 결정해야하는 부분이다. 따라서 최적매개변수을 선정하기 위해 실험표를 구성하고 모델 개선에 따라 자료동화 효과가 미치는 영향에 대해서도 실험을 진행하였다. 이어도 과학기지를 포함한 한반도 주변으로 구축된 FVCOM 조석모델과 조화분해를 통해 재생산한 수층별 유속자료를 바탕으로 Table 2와 같이 실험표를 구성하였다. Table 2에서 알 수 있듯이 Correlation length(R)를 10 km~100 km까지, Scaling factor(Ga)를 0.1~4까지 조절하면서 실험을 진행하고 자료동화를 미적용한 실험결과를 포함한 총 25개 결과를 종합하여 관측 정점별 최적의 조건을 찾는다.
추가적인 실험으로서 해양자료동화의 효과가 배경 모델이 수반하는 정확성의 차이에 따라 어떻게 반응하는지 확인하였다. 일반적으로 해양수치모델은 개방경계조건과 초기조건에 따라 연안에서의 정확성이 결정되는데 초기조건과 지형조건을 고정하고 오직 개방경계조건만으로 조석에 대한 검증을 2가지로 나누어 실시하였다. 즉, 서로 다른 2개의 정확도를 가진 배경 모델을 준비하고 상대적으로 정확도의 차이가 난 상태에서 앞서 구성한 총 25개의 자료동화 실험을 각각 수행했다. Fig. 4에서 사전 검증된 개방경계조건의 기존 평균 제곱근 오차(진폭 0.05 m, 위상 0.86도)보다 4배 이상 크기를 가지는 추가 개방경계조건을 준비하였다(진폭 0.19 m, 위상 6.45도). 본 실험을 통해 배경 모델이 가진 자체 정확도가 자료동화 적용시 최적매개변수에 대한 변화를 유도하는지 분석하였다.
자료동화를 적용하는 총 24개의 모의 결과를 바탕으로 Taylor(2001)가 개발한 Taylor diagram을 활용하여 최적매개변수를 산정하였다. Taylor diagram은 다수의 시계열자료 가운데 통계학적 개념을 바탕으로 절대참값으로 가정하는 관측값과 가장 근접한 실험 조건을 선정하는데 활용가능한 Diagram이다. Taylor diagram에서는 고정된 관측값과 다수의 배경값 사이의 상관계수와 각각의 표준편차 그리고 중앙 평균 제곱근 오차를 계산하여 이를 하나의 Diagram에 표시한다. Taylor diagram의 최종결과를 통해서 24개의 실험조건 중에서 관측자료와 가장 상관도가 높고 편차가 적으며 오차가 낮은 실험 조건를 찾는데 매우 효과적인 장점을 가지고 있다.
최적매개변수 산정에서 Taylor diagram을 사용하는 이유는 다수의 시계열 자료 가운데 필요한 최적매개변수을 시각적으로 쉽게 찾을 수 있고 이는 배경값과 관측값의 정확한 상관분석이 가능하기 때문이다. 국지적으로 자료동화 적용시 요구되는 최적매개변수를 찾기 위해서는 다양한 경험적 연구가 필요하고 이 빈도는 크면 클수록 최적화된 매개변수값을 산정할 수 있기 때문에 Taylor diagram 분석이 적합하다.
4. 연구 결과
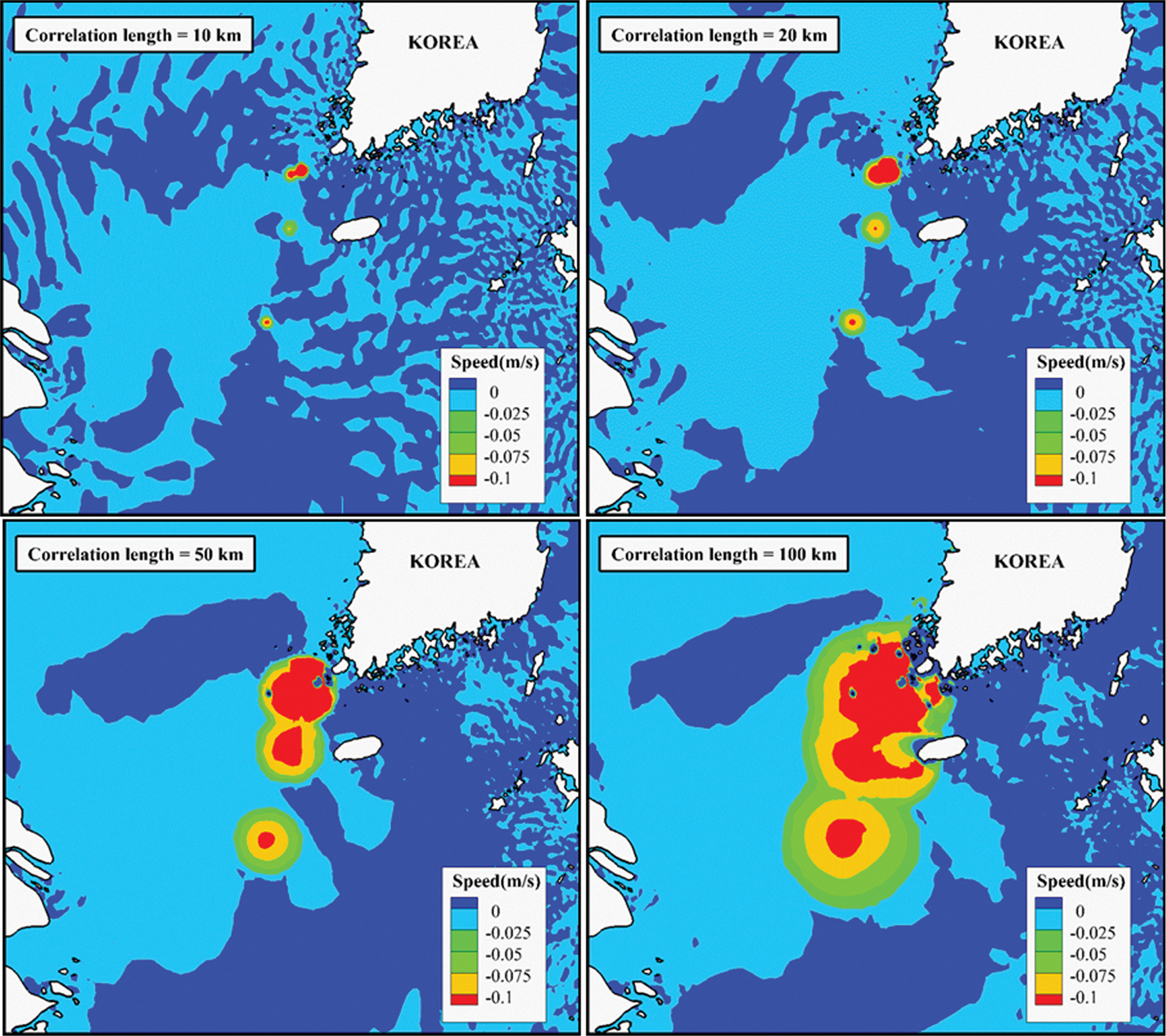
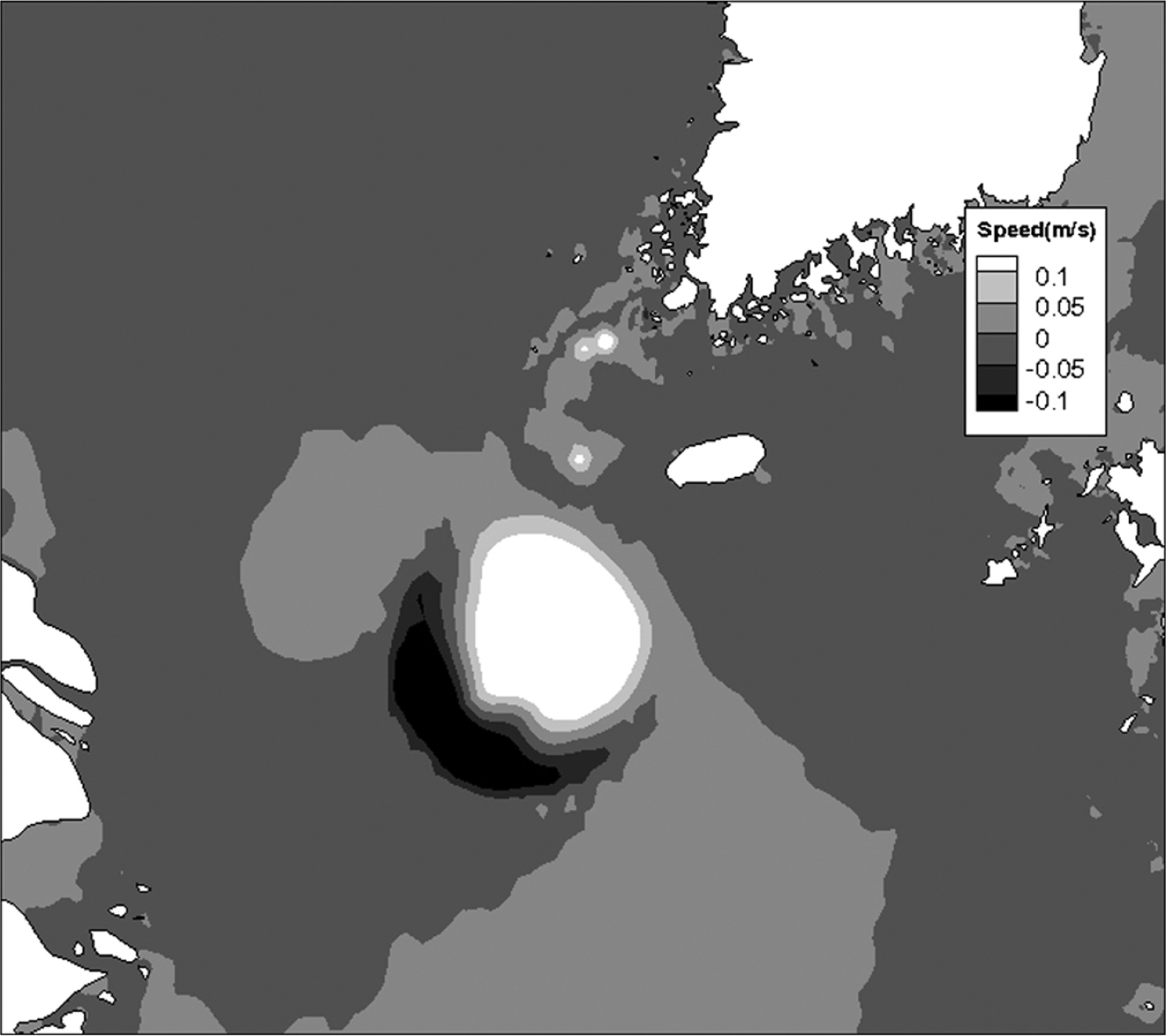
자료동화 효과를 파악하기 위해 자료동화 적용 전/후 유속 크기의 공간분포 차이를 Scale factor 0.5를 기준으로 Correlation length 별로 분석하였다(Fig. 6). 관측정점을 기준으로 Correlation length 범위 내로 10 cm/s 이상의 유속차이가 나타났고 모의기간 중 최대 2 7 cm/s 유속을 나타났다. Scale factor가 고정인 상태에서 Correlation length가 커짐에 따라 1번 정점부터 3번 정점까지 점차 상관범위가 중첩되는 현상이 나타나고 이로 인해 최대유속차이 분포가 Correlation length보다 커지기도 한다.
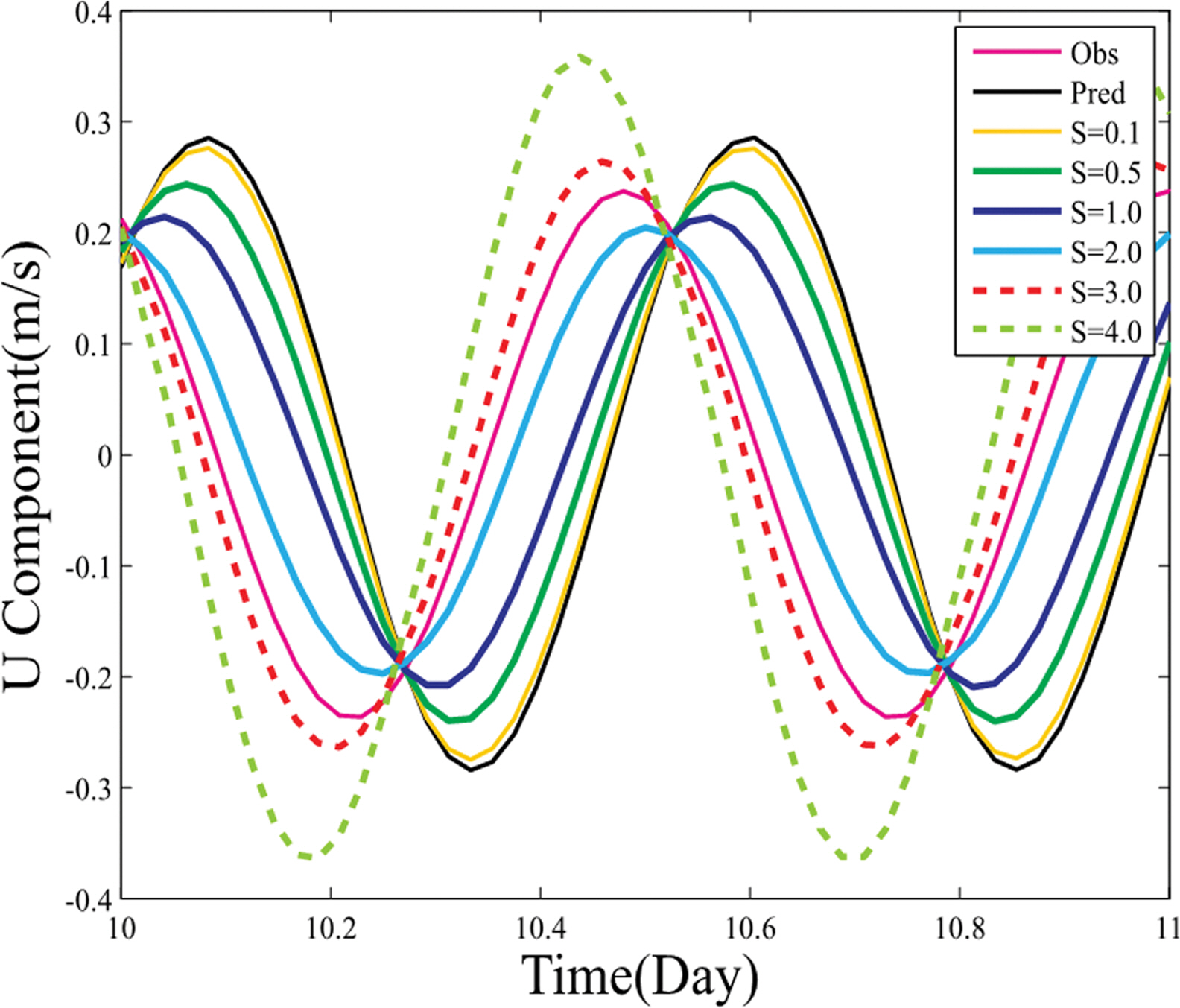
모든 정점마다의 Correlation length을 고정하고 Scale factor에 따른 유속 성분 시계열을 비교해볼 수 있다. 예를 들어 이어도 과학 기지에 위치한 4번 정점을 기준으로 총 25가지의 실험결과에서 Correlation length가 20 km일 때, Scale factor에 따른 결과차이를 보면 Scale factor가 점점 증가하면서 배경값이 관측값과 근사해지는 것을 알 수 있다(Fig. 7). 하지만 매 정점마다 유속벡터별 2가지의 매개변수를 고정시켜가면서 다수의 시계열을 비교하는 것은 정확한 최적매개변수를 산정하는데 어려움이 있다. 따라서 시계열분석을 통해 최적매개변수을 산정하는 것이 아닌 Taylor diagram을 통한 통계적접근으로 Correlation length와 Scale factor의 최적값을 산정하였다.
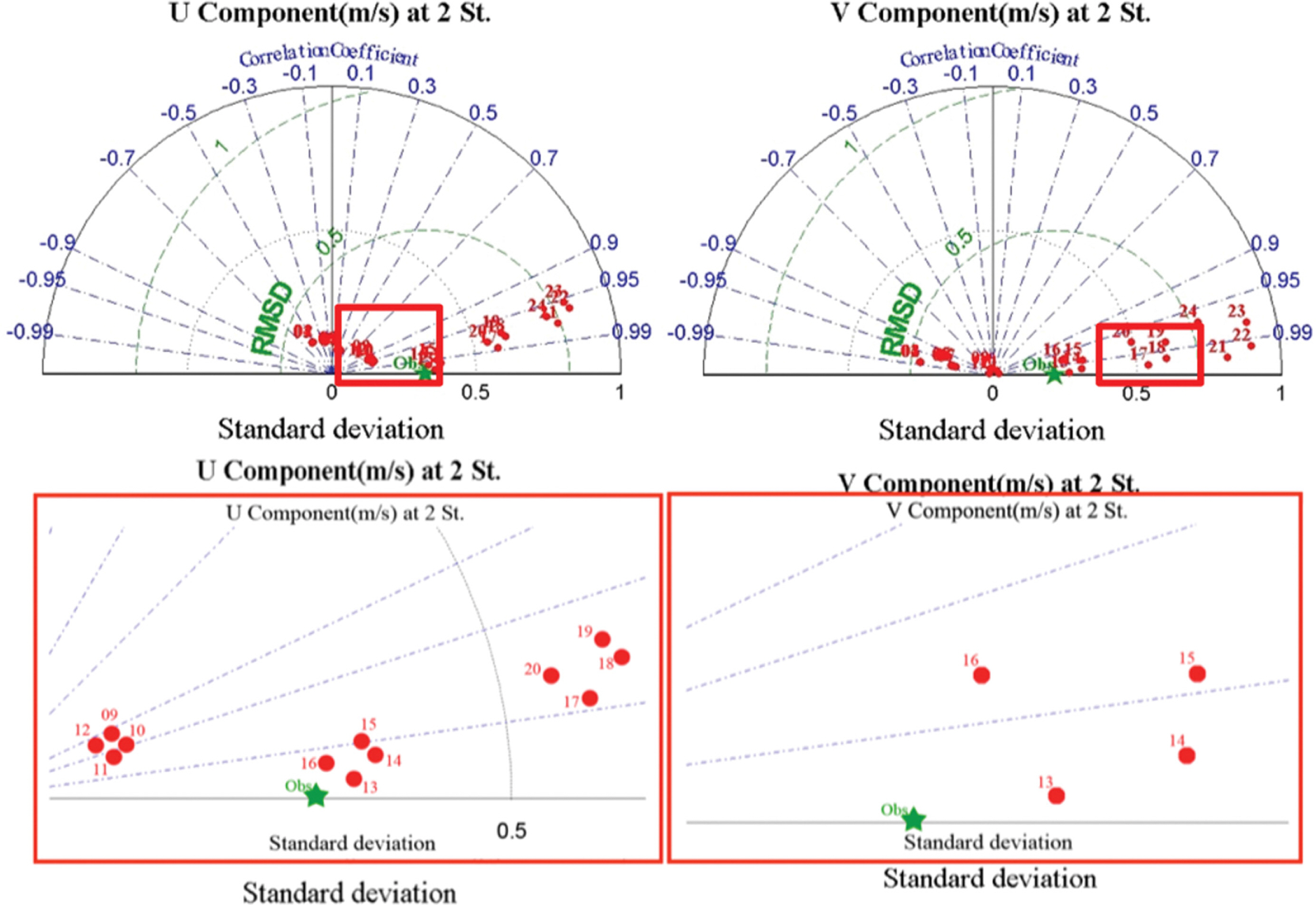
총 25가지의 실험결과를 시계열로 표현하고 이를 비교해본 결과, 관측지점별로 도출된 최적의 Scaling factor와 Correlation length는 각각 다르다는 것을 알 수 있다. 최적매개변수 산정을 위한 Taylor diagram을 표현하기 위해 표준편차와 중앙 평균 제곱근 편차 그리고 상관계수를 계산하였다. Fig. 8을 예를 들면, 2번 관측정점에서 유속 벡터성분별 관측값과 가장 상관도가 높고 편차가 적은 실험은 Taylor diagram을 통해 확인해볼 경우 13번 실험이 가장 관측값과 유사도가 높다. 즉, 2번 정점에서는 13번 실험에 사용된 매개변수가 최적매개변수라 할 수 있다.
추가적인 실험으로 조석검증이 진행되기 전의 배경 모델과 검증된 배경 모델을 사용하여 각각의 자료동화 적용 결과를 비교하였다. Table 3에서는 배경 모델의 정확성 개선 후 변동된 관측 정점별 최적매개변수를 제시하고 있다. 1번 정점의 경우 배경 모델의 정확성이 개선됨에 따라 요구되는 Correlation length의 최적값이 상대적으로 감소하였다. 2번 정점의 경우에는 Correlation length의 차이는 없지만 요구되는 Scale factor가 감소되었다. 3번 정점에서는 차이가 없었으나 이어도 과학 기지에서는 요구되는 Scale factor의 최적값이 감소되었다. 결과적으로 조석검증을 통해 배경 모델의 정확성이 증진됨에 따라서 요구되는 최적매개변수의 값들이 감소하는 특징이 나타났다.
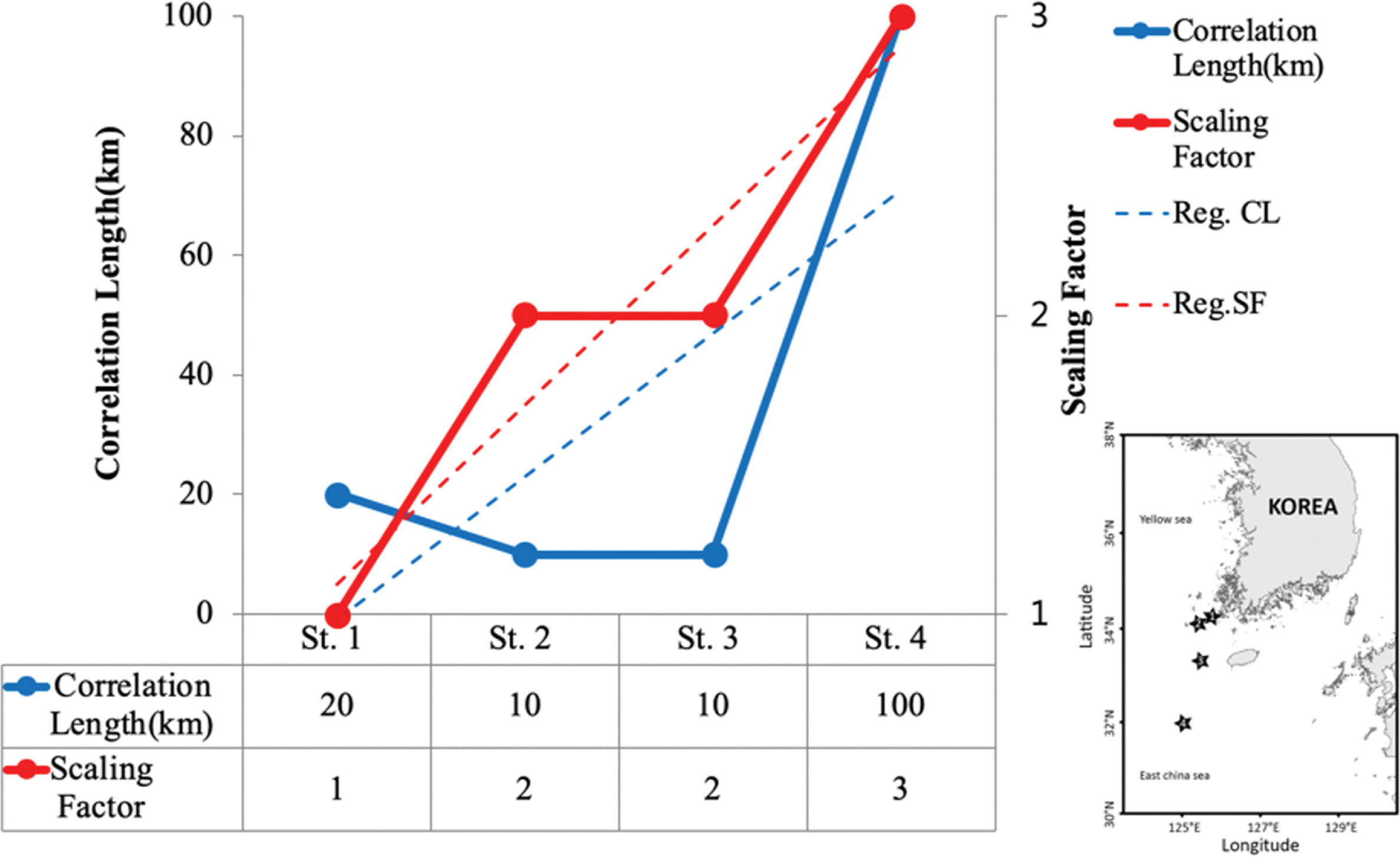
Taylor diagram을 통해 빠르고 정확하게 정점별 및 성분별 최적매개변수를 찾을 수 있으며 본 연구에서는 Fig. 9처럼 종합적으로 정점별 최적매개변수를 제시하였다. 이를 보면 알 수 있듯이 최적매개변수의 특징은 연안에서 제일 가까운 1번 지점부터 가장 멀리 떨어진 이어도 과학 기지(4번 정점)까지 진입할수록 Scale factor가 1에서부터 3까지 점진적으로 증가하는 경향을 보인다. Correlation length의 최적값은 연안과 가까운 정점들에서 10~20 km을 보이고 외해 관측 정점인 이어도 과학기지에서는 100 km을 보임으로써 연안과 외해에서의 최적값의 차이가 나타났다. 이 밖에도 공통점으로서 모든 정점에서의 유속에 대한 북방성분과 동방성분에 대해서는 모두 같은 값의 Scaling factor와 Correlation length가 최적의 조건으로 나타났다.
5. 결론 및 고찰
광역 모델 기반에서의 조석에 대한 재현 및 예측 향상을 위해 자료동화기법 중 하나인 최적내삽법을 적용하였고 자료동화에서 요구되는 국지적 최적매개변수를 산정하였다. 최적내삽법에 필요한 Scaling factor와 Correlation length는 관측정점의 위치에 따라 요구되는 최적값이 상이하다. 본 연구 결과에 따르면 연안에 근접한 관측 정점에서의 Correlation length 최적값은 10~20 km이다. 이는 관측정점 주변 연안에서 조석에 의한 해류의 영향 범위는 최대 20 km을 넘지 않는다는 것을 의미한다. 최적값이 외해 정점과 상대적으로 작은 이유는 연안에 가까울수록 조석 기인의 해류 성분이 증가하고 동시에 연안의 복잡한 지형적 특성으로 나타나는 간섭으로 인해 비선형성이 커지기 때문이다. 더불어 이미 외해 정점에서의 자료동화가 동시에 적용되었고 이는 즉, 외해 정점에서 전파되는 개선된 조석류가 연안까지 전달됨에 따라 연안 정점에서 관측값과 오차가 줄어들어 상대적으로 최적화 요구량이 적어지는 효과도 있다. 따라서 외해에 위치한 관측정점의 최적매개변수는 조석경계조건이 연안역까지 정상적으로 도달하기 위해 상대적으로 요구되는 값이 높다는 것을 의미한다.
기본 시스템인 즉, 배경 모델이 기본적으로 가지고 있는 정확성이 향상될 수록 매개변수의 최적값이 감소한다. 검증된 모델을 바탕으로 자료동화를 적용할 경우, 관측값과 배경값의 차이인 오차가 줄고 배경오차공분산 또한 관측오차공분산보다 상대적으로 줄어들기 때문에 결과적으로 비중함수가 관측보다는 모델측에 신뢰를 더 두게 됨으로써 요구되는 Scaling factor와 Correlation length의 최적값이 줄어든다. 이를 확인해보기 위해 추가 연구를 진행해본 결과, 유속자료동화의 성능도 배경 모델이 실제 시스템과 가까울수록 향상됨을 확인하였다. 따라서 배경 모델이 과거 관측값으로부터 얼마나 유사한지에 따라서 배경오차공분산이 결정되고, 이에 따라 최종 예측 성능도 좌우된다. 즉, 자료동화의 성능은 시스템 모델(배경모델)이 실제 시스템(관측값)과 가까울수록 좋아진다. 결론적으로 해양자료동화에서 첫번째로 확인해야할 사항은 기본 모델의 정확성이며 특히, 서남해안과 같은 복잡한 해안선 및 불규칙한 지형적 특성에서 정확성을 확보하기 위해선 비구조격자체계 해양모델이 기반 모델로써 적합하다.
Cressman analysis에서 사용된 Total weight function의 가장 큰 장점은 계산 구조가 간단하기 때문에 수치해석적으로 계산이 용이하다는 점이다. 하지만 이는 Correlation length에 의해 절점에서 추정값에 대한 계산여부가 결정되기 때문에 Correlation length 범위 외에 위치한 절점에서는 자료동화가 아예 적용되지 않아 계산비용 절감효과를 낳는 것이다. 따라서 위성자료가 아닌 mooring 연속 자료와 같은 소수의 관측정점을 가진 지역에서 Cressman method을 적용할 경우에는 불연속적인 예측 결과를 보여줄 수 있다. 외해에 위치한 관측정점의 경우에는 Correlation length에 따라서 개방경계조건을 변형시켜 연안으로 전달시킬수 있고 연안에 위치한 관측정점은 그 범위가 서로 중첩될 경우 비선형성을 증폭시켜 예측 결과가 상이할 수 있다. 따라서 관측정점에 대한 Correlation length의 최적값은 Cressman analysis에서 중요한 매개변수이며 최적값을 산정하기 위해서는 반드시 관측정점 주변의 물리적 특성을 고려해야한다.
본 연구에 사용되는 모든 관측값은 사이거리만을 기준으로 중첩되지 않는 범위내에 최적값을 산정하였다. 즉, Correlation length가 다른 관측정점의 상관길이 범위내로 포함되지 않게 구성하였다. 따라서 향후에는 상관길이의 범위가 중첩될 경우에 대한 추가적인 연구가 필요하다. 현재는 본 연구를 바탕으로 산정된 최적매개변수를 각 정점별로 적용하도록 시스템을 개선하였으며 자료동화 적용시 중첩영역에 대한 최적매개변수 산정에 대한 구체적인 연구는 진행중에 있다(Fig. 10). 추가로 연안에서 관측할 수 있는 수층별 연속 유속자료뿐만 아니라 수온과 염분에 대한 자료동화 연구도 함께 진행할 예정이다.