1. 서 론
자연해안의 경우 해안선이 먼 바다를 향해 번갈아가며 나가고 들어오는 현상이 흔히 관측되며 이러한 원호모양 해안선은 beach cusp이라 불린다(Cho, 2019b). 현재 우리나라 동해안의 여러 백사장 중 아직 개발의 손길이 미치지 못해 자연표사 계에 가깝게 보존된 맹방해안에서도 상당히 다양한 크기의 beach cusp을 관측 할 수 있다(Cho, 2019b). 자연해빈은 고파랑에 의해 일시적으로 침식되더라도 너울이 우월한 해양환경에서 장기간에 걸쳐 복원된다(Cho and Kim, 2019; Cho et al., 2019; Cho, 2019a). Beach cusp은 전술한 일년에 걸친 해빈 대순환과정을 구성하는 중요한 요소라는 점에서 맹방해안 beach cusp의 생성기작으로 알려진 Synchronous Edge wave의 수리특성을 살펴보는 작업은 상당한 공학적 가치를 지니며, 해빈침식 대응방안 최적화 과정에도 적지 않은 역할을 수행할 수 있을 것으로 판단된다(Cho, 2019b).
최근 해안공학 계에서는 beach cusp은 Edge waves에 의해 기인되는 것으로 보는 시각이 주류를 이룬다. Beach cusp의 생성기작으로 Edge waves의 가능성을 맨 처음 제기한 이는 Guza(1974)로, 이 연구에서 Guza(1974)는 포획모드 Edge waves에 의해 재배치되는 해빈 표사와 이로 인해 형성되는 beach cusp을 이동상 수리실험을 통해 예증한 바 있다. Guza(1974)에 따르면 영의 영각으로 내습하는 외중력파에 상당한 세기의 반사파가 더해져 정상파동계가 전빈에 형성되고, 이어 정상파동계를 구성하는 외중력파 사이에 resonance triad 혹은 quartet가 충족되는 경우 출현하는 포획모드 Edge waves에 의해 beach cusp은 초기화된다(Cho, 2019b). 전술한 subharmonic Edge waves는 표사계에 beach cusp이라는 흔적을 남기고 소멸되며, 이 후 이렇게 초기화된 beach cusp은 내습하는 파랑과 동일한 주기를 지니는 Synchronous Edge waves에 의해 유지된다.
따라서 적지 않은 에너지 소산을 수반하는 plunging 혹은 collapsing 형태의 쇄파가 진행되는 경우 Edge waves가 출현할 수 있는 가능성은 상당히 낮아지며, 주로 surging 형태의 breaker 로 이어지는 천수과정에서 sub-harmonic Edge wave가 발생한다. 그러나 beach cusp을 초기화하고 소멸되는 짧은 지속기간으로 인해 현장 관측 자료에서 sub-harmonic Edge wave는 잘 드러나지 않은 경우가 대부분으로, 이로 인해 현재 전술한 인과관계에 대해 의문을 제기하는 이도 있으나, Edge waves에 의해 결과되는 beach cusp으로 보는 시각이 현재 해안공학계의 정설로 간주되는 듯하다(Guza, 1974; Dodd et al., 2008).
전술한 계측의 어려움을 극복하기 위해 최근 Cho(2019b)는 surging 형태의 breaker와 장주기 외중력파가 우월한 해양환경에서 출현하는 sub-harmonic Edge wave의 특성을 활용하여 파랑관측 자료(Cho and Kim, 2019)와 실측된 해안선 위치(Cho et al., 2019)을 활용하여 맹방해안에 형성되는 beach cusp의 일 년에 걸친 대순환 과정과 계절별 특성, beach cusp의 여러 생성기작 중 포획모드 Edge waves를 중심으로 Edge waves에 의해 결과되는 beach cusp의 상관관계를 살펴본 바 있다.
이 연구에서 Cho(2019b)는 Eckart(1951)와 Guza(1974)의 천수방정식 해석해에 기초하여 맹방해빈 전빈 폭으로부터 맹방해빈에 출현할 수 있는 포획모드 Edge waves의 주기와 resonance quartet을 구성하는 입사파 주기를 가늠하고, 포획모드 Edge waves를 야기하는 입사파는 주기는 28.9 s 내외인 외중력파로 특정 하는 등 적지 않은 성과를 거둔 것으로 보인다.
또한 맹방해안에서 형성되는 beach cusp은 다수의 sand wave가 하나로 융합되는 과정과 이렇게 융합된 하나의 커다란 sand wave가 다시 여러 개의 작은 sand wave로 나뉘는 과정이 반복되며, 고파랑에 의한 대규모 침식으로 해빈이 재정렬되는 과정에서 역동적인 모양의 beach cusp은 소멸되며, spectral mean sand wave NO의 시계열자료로부터 beach cusp의 대순환과정은 일 년에 두 번에 걸쳐 진행된다는 사실 등도 확인된 바 있다.
그러나 Cho(2019b)는 간헐적으로 출현하여 직접 관측이 어려운 sub-harmonic Edge waves의 특성으로 인해, Edge waves를 결과하는 외중력파를 중심으로 Edge waves와 beach cusp의 상관관계를 간접적으로 다루었을 뿐 beach cusp을 유지하는 것으로 전해지는 Synchronous Edge waves를 직접 다루지는 못한 것으로 보인다. 이러한 결과는 한 시간 간격으로 통계처리 된 파랑정보만을 다루며, 원시자료는 제공되지 않은 우리나라 파랑관측 관행에 일정부분 기인된 것으로 보이나 beach cusp이 Synchronous Edge wave에 의해 유지된다는 사실을 상기하며 Synchronous Edge waves의 수리특성을 밝히는 작업은 상당한 공학적 가치를 지닌다.
이상의 논의를 토대로 본 논문에서는 맹방해빈에서 형성될 수 있는 Synchronous Edge waves의 수리특성을 수치해석에 기초하여 살펴보려 한다. 수치모의는 OpenFOAM에 기반 한 tool box인 IHFOAM에 준거하여 수행되며, 파랑모형은 RANS(Reynolds Averaged Navier-Stokes equation)와 질량 보존식으로 구성된다.
2. Synchronous Edge Waves와 Beach Cusp의 상호작용
이해를 돕기 위해 synchronous Edge waves에 의해 beach cusp이 유지되는 과정을 단계별로 정리하면 다음과 같다(Guza, 1974; Dodd et al., 2008; Cho, 2019b).
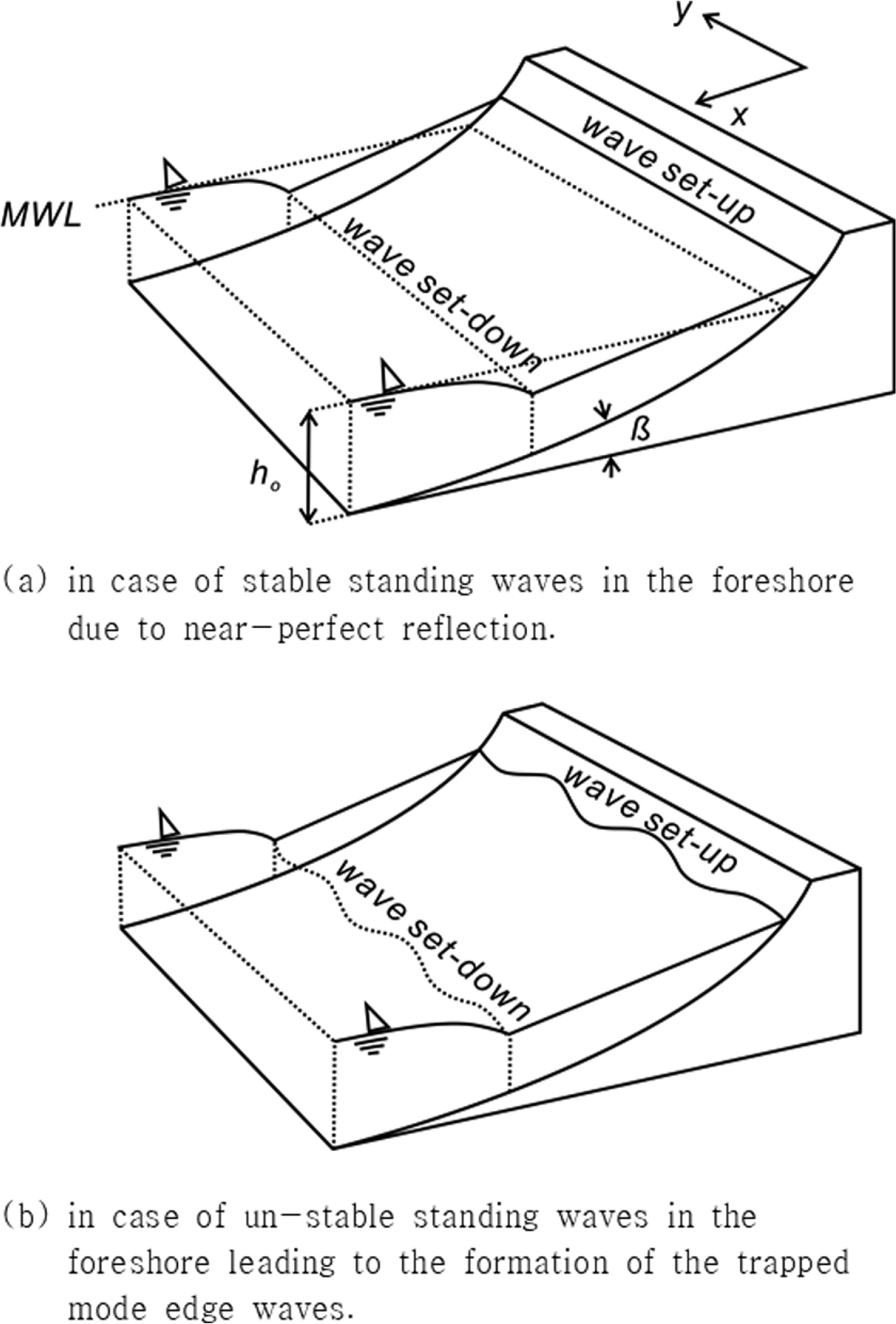
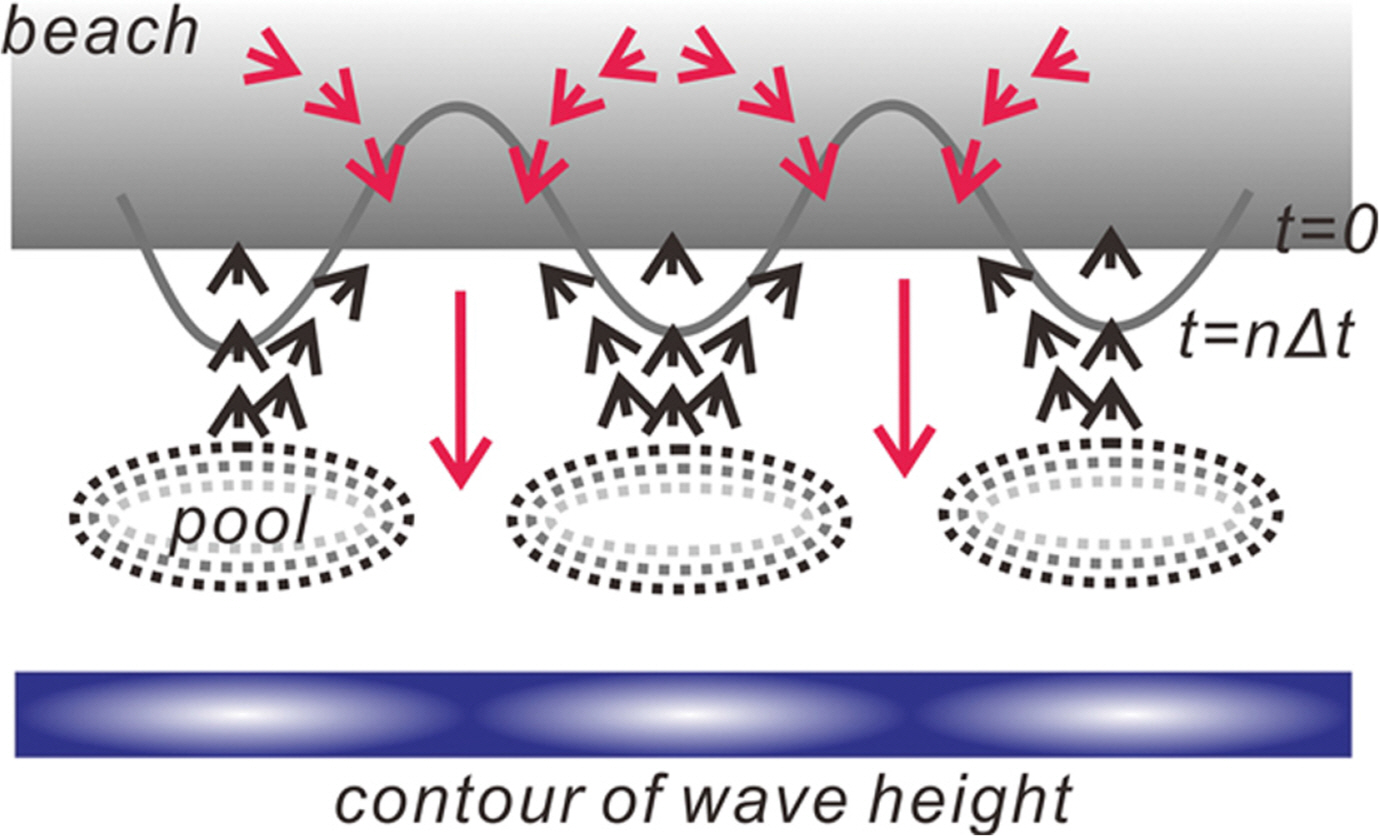
A. 파고가 연안방향으로 일정하지 않은 파랑이 영의 영각으로 내습하는 경우 상대적으로 큰 파고에 노출된 영역에서는 처오름 높이가 상대적으로 크며, 이 경우 처오름[up-rush] 정점에서 흐름은 양쪽의 분산단면으로 방향을 틀어 처오름 높이가 작은 영역으로 나뉜다[Fig. 1, 2 참조].
B. 이렇게 집수가 이루어지는 해역에서는 처내려지는 흐름[back-wash는]의 강도는 증가하며, 이로 인해 집수 해역에는 만이, 높은 처오름이 진행되는 해역에는 돌출부가 형성되며, 돌출부에서는 처오름[up-rush] 정점에서 바뀐 흐름 방향으로 인해 먼 바다로 회귀되는 back-wash의 세기는 감소된다[Fig. 1, 2 참조].
C. 전술한 집수효과로 만에서 한층 강해진 back-wash는 후행하여 접근하는 파랑으로 인한 up-rush를 제한함으로써 내습하는 파동계와 교감하며 결국 이러한 되먹임으로 인해 전빈 파동계에는 Synchronous Edge waves와 유사한 파동이 출현하고 beach cusp은 유지된다[Dodd et al., 2008].
3. 수치모형
수치모의는 OpenFoam 기반 Tool box인 IHFoam에 준거하여 수행되며(Losada et al., 2008), IHFoam에서 파랑모형은 RANS(Reynolds Averaged Navier-Stokes equation)와 질량 보존식으로 구성되며, 자유수면은 VOF(Volume Of Fraction) 법을 활용하여 추적된다. 난류모형으로는 k-ε 모델을 차용하였다.
IHFoam(Losada et al., 2008)을 구성하는 파랑모형인 RANS, 연속 방정식을 기술하면 다음과 같으며,
여기서 U는 속도벡터, g는 중력가속도벡터, X는 위치벡터를 각각 나타낸다. μeff는 μ + ρνturb로서 동점성계수, p*는 유사동압력을 각각 나타낸다.
이상 유체를 해석하기 위한 VOF 식을 기술하면 다음과 같으며,
여기서 γ는 단위격자 체적에서 물이 차지하는 비율을 나타낸다.
3.1 Energy absorbing boundary condition
계산영역내부에서 반사되어 먼 바다로 회귀하는 반사파가 개방경계에서 적절히 제어되지 못하는 경우 수치모의는 왜곡될 수 있으며, 전술한 반사파를 제어하는 방법은 크게 passive wave absorbers와 active wave absorption 등으로 분류할 수 있다. Artificial beach, 다공성 물질, 다공성 판, 수치적으로 감소 등이 passive wave absorbers에 해당하나, 전술한 방법으로는 접근하는 파랑 에너지의 소산을 완벽하게 구현하는 것은 어렵고 어느 정도의 수치적 반사가 발생하기 마련이다. 특히, 장주기파의 경우 artificial beach는 취약하며 상당한 수치적 반사가 생성되는 것으로 전해진다(Pengzhi and Liu, 1999; Lara et al., 2006; Wei and Kirby, 1995; Losada et al., 2008).
이에 비해 active wave absorption은 조파 피스톤의 움직임을 측정된 파랑 세기에 맞게 조절하여 계산영역 내부로부터 접근하는 파랑의 수치반사를 억제하는 방법으로, 초기에는 수리모형실험에서 활용하기 위해 개발되었으나, 이 후 수치모형으로 확대되었으며 조파 경계와 개방 경계에 적용가능하며, 경계에 적절한 유속성분을 수치적으로 부과하는 경우, 파랑을 효과적으로 흡수할 수 있는 것으로 알려진 바 있다.
Active wave absorption systems의 유도과정을 정리하면 다음과 같다:
먼저 다음과 같이 정의되는 수심평균 연속방정식으로부터
다음과 같은 관계식을 얻을 수 있다.
파속 c는 선형이론으로부터 다음과 값이 기술될 수 있으나,
여기서 파속 c는 천해역에서 g h
반사파 제어를 위해 경계에서는 접근하는 파랑과 반대방향으로 접근하는 파랑과 같은 속도를 지니는 가상의 파랑이 조파되며, 식(5)를 반사파 파고 ηR을 중심으로 기술하면 다음과 같이 전환되며,
여기서 Uc는 경계에서 수직하게 계산영역 내부를 향하는 교정 속도를 나타내며, 반사파 파고 ηR는 다음과 같이 산출할 수 있다.
식(9)에서 ηM는 관측된 파고, ηT는 목표파고를 각각 나타낸다. 그러나 대부분의 경우 반사파랑은 개방경계 혹은 조판경계로 직각으로 접근하는 것은 아니므로, Schaffer와 Klopman(2000)은 식(9)를 다음과 같이 일반화 하였으며,
여기서 ∆β는 접근 파랑의 입사각을 나타낸다.
4. 수치모의
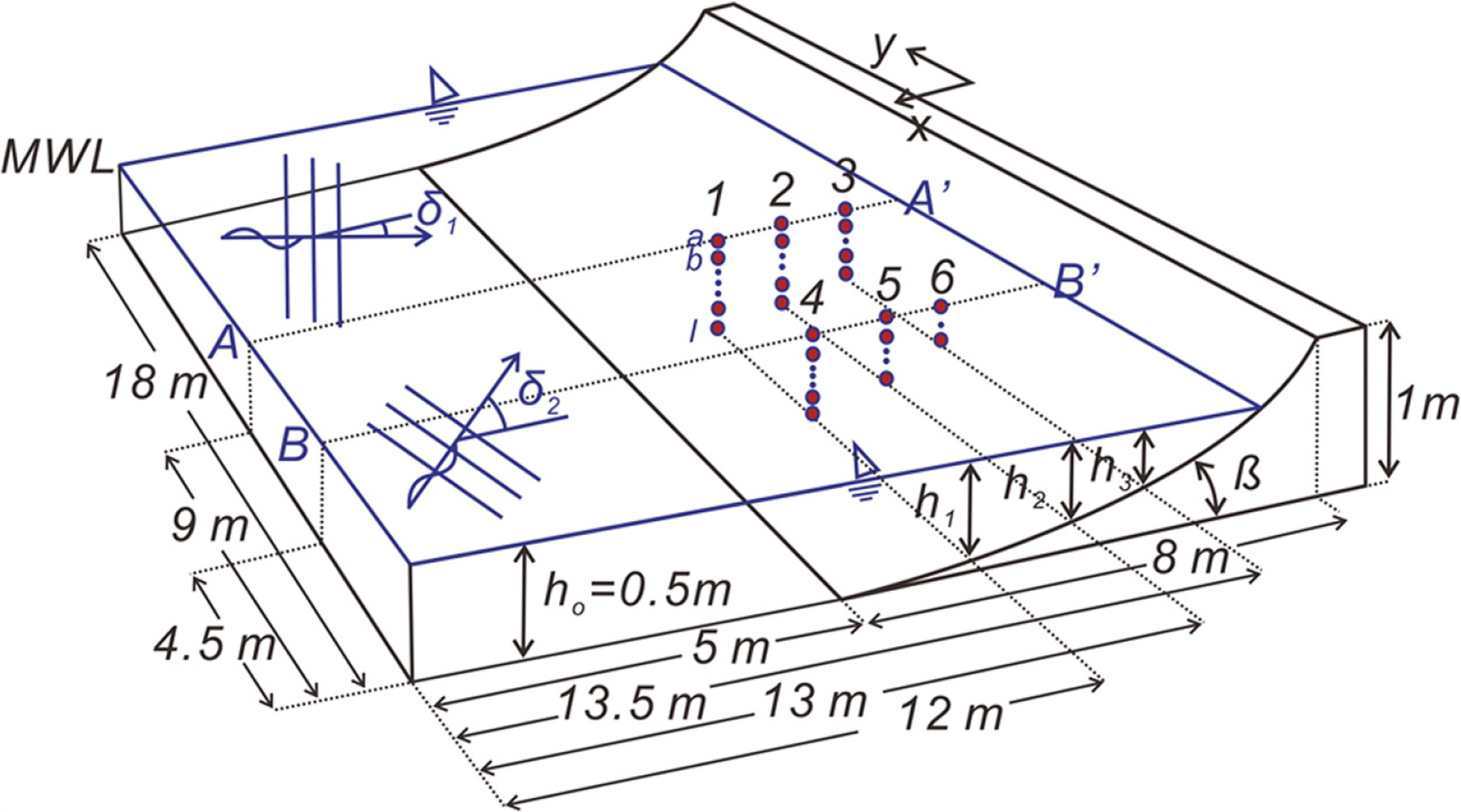
Sub-harmonic edge wave에 의해 초기화된 beach cusp을 유지하는 기작으로 알려진 Synchronous Edge waves의 수리특성을 살펴보기 위해 경사가 1/m인 단조 해안에서의 surging 형태의 breaker로 이어지는 천수과정, 처오름, 처내림 과정을 수치 모의하였다. 해안선으로부터 60~80 m 이격된 지점까지 경사가 1/8 내외인 급경사의 전빈이 포진하며 이 후 수심이 5 m 내외인 간조단구[low tide terrace]가 길게 이어지는 맹방해빈 전빈특성과 간조단구에서의 수심을 고려하여 파형은 Korteweg-de Vries 식의 해석해로 정의되는 Cnoidal wave로 취하였다(Cho, 2019b). 해빈경사는 1/8로 선정하였으며, 과다한 계산량을 피하고 보다 효율적인 수치모의를 위해 수심은 0.5 m로 선정하였으며, 이는 1/10 Scale에 해당한다. 수치모의에 사용된 numerical wave basin은 Fig. 3에 도시하였으며, 계산영역은 1,250,000 여개의 격자를 이용하여 이산화 하였으며, 수치수조의 좌안과 우안, down-wave side 개방경계에는 3.1절에서 다룬 Energy absorbing boundary condition을 부과하여 수치적 반사가 최소화 되도록 노력하였다.
Surging 형태의 breaker로 이어지는 천수과정과 장주기 외중력파가 우월한 해양환경에서 출현하는 sub-harmonic edge wave의 특성을 고려하여 주기에 변화를 주어 총 세 번의 수치모의를 수행하였으며, Table 1에는 수치모의에 사용된 해빈 경사, 파랑조건, Iribarren NO. ξ를 수록하였다. Surging 형태의 쇄파는 ξ > 3.3인 경우에 발생하며, Table 2에는 Iribarren NO. ξ에 따른 쇄파형태의 변화를 정리하였다.
Iribarren NO. ξ는 심해파고 Ho와 심해에서의 파장 Lo으로 기술하는 경우 다음과 같이 정의되며
여기서 심해 파장 Lo은 다음과 같이 산출될 수 있다.
유한수심에서의 대표적 비선형 파랑모형인 Cnoidal wave를 기술하면 다음과 같으며,
여기서 ζ는 해수면 변위, H는 파고, Ch은 Jacobi elliptic function, c는 파속, L은 파장, T는 주기, M은 0과 1 사이의 값을 지니는 elliptic parameter를 각각 나타낸다. KM은 제1종 타원적분, EM은 제2종 타원적분을 각각 나타내며, KM과 EM은 M 값에 종속한다. Cnoidal wave 파형은 M이 0에 수렴하면 StokesⅠ파형에, M이 1에 수렴하면 Solitary wave 파형에 수렴한다.
Cnoidal wave에서의 유속은 다음과 같이 기술될 수 있으며
여기서 ζx, ζxx, ζxxx는 x에 대한 자유수면의 1차, 2차, 3차 도함수, ·
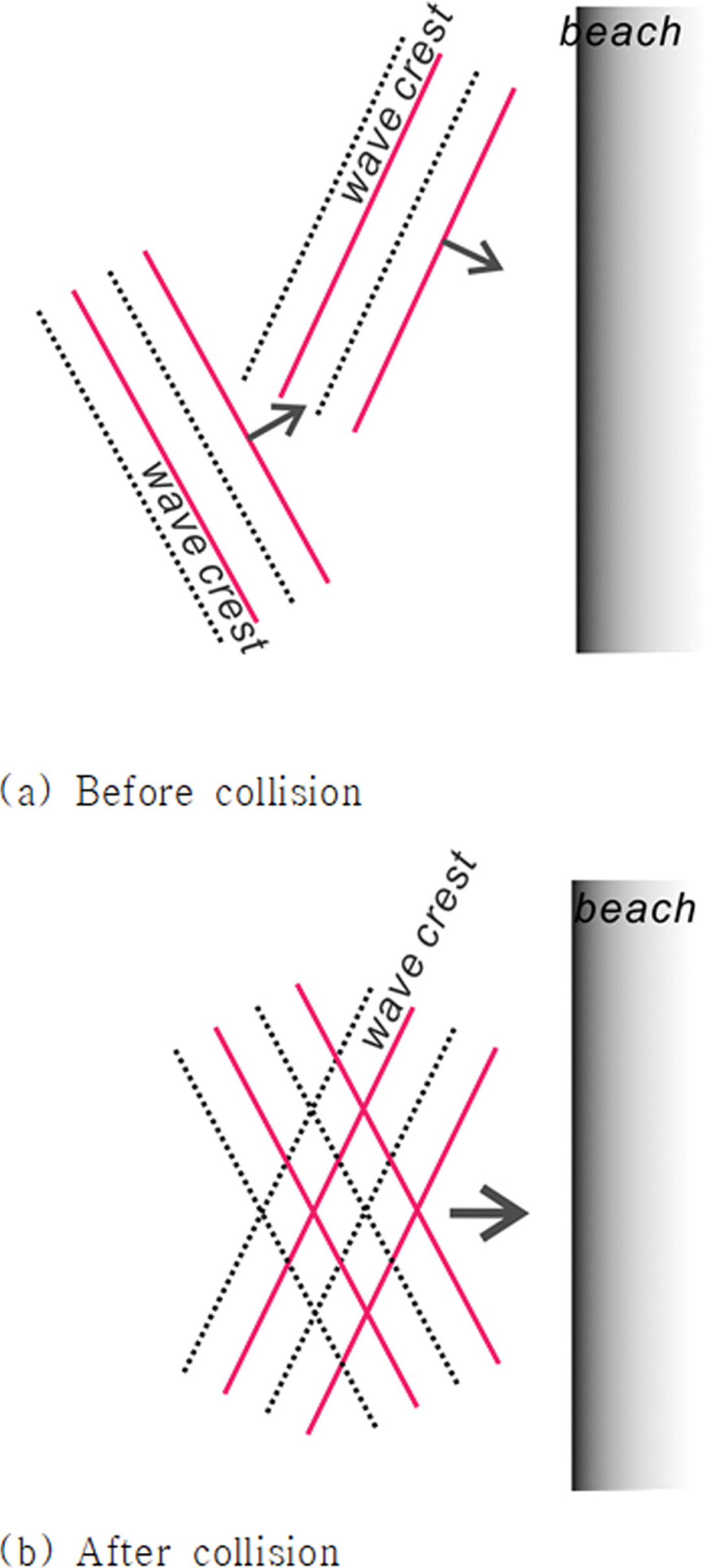
4.1 Short-crested wave
2장에서 살펴보았듯 Synchronous Edge waves가 형성되기 위해서는 연안방향으로 파고가 변조되어야 하며. 본 논문에서는 전술한 short-crested waves를 재현하기 위해 동일한 주기와 파고를 지니는 두 개의 Cnoidal wave가 전면 해역에서 비스듬히 조우되도록 조파하였으며 Colliding Angle은 θ = 140°[θ = π - δ1 - δ2]로 조절하였다. 이는 δ1 = 20°, δ2 = - 20°에 해당되며[Fig. 3 참조], Fig. 4에는 이해를 돕기 위해 비스듬히 조우하는 두 개의 Cnoidal wave로 인해 전면 해역에 형성되는 short-crested waves의 개념도를 수록하였다.
4.2 수치결과 및 분석
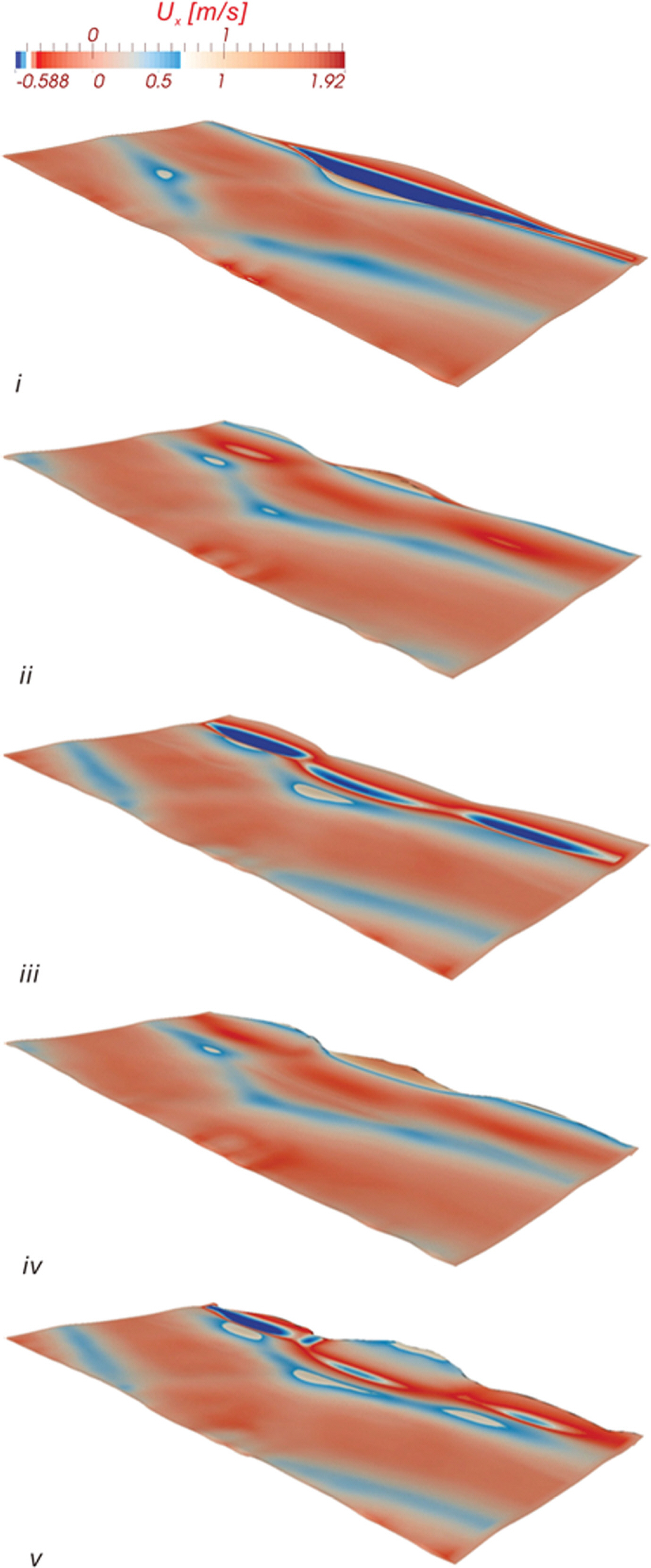
Fig. 5에는 RUN1에서 관측된 자유수면 snapshot을 순차적으로 도시하였으며 전면 해역에서 형성되는 short-crested wave와 해안과 나란한 방향으로의 처오름 높이 차이로 인해 형성되는 Synchronous Edge waves를 관측할 수 있다.
Fig. 6에는 RUN 2에서 관측된 자유수면 snapshot과 해안방향 유속 Ux 등고선 도를 순차적으로 도시하였다. 상대적으로 긴 주기로 인해 RUN 1에 비해 보다 역동적인 처오름 과정이 관측되며 처오름 높이가 증가하는 것을 관측할 수 있다.
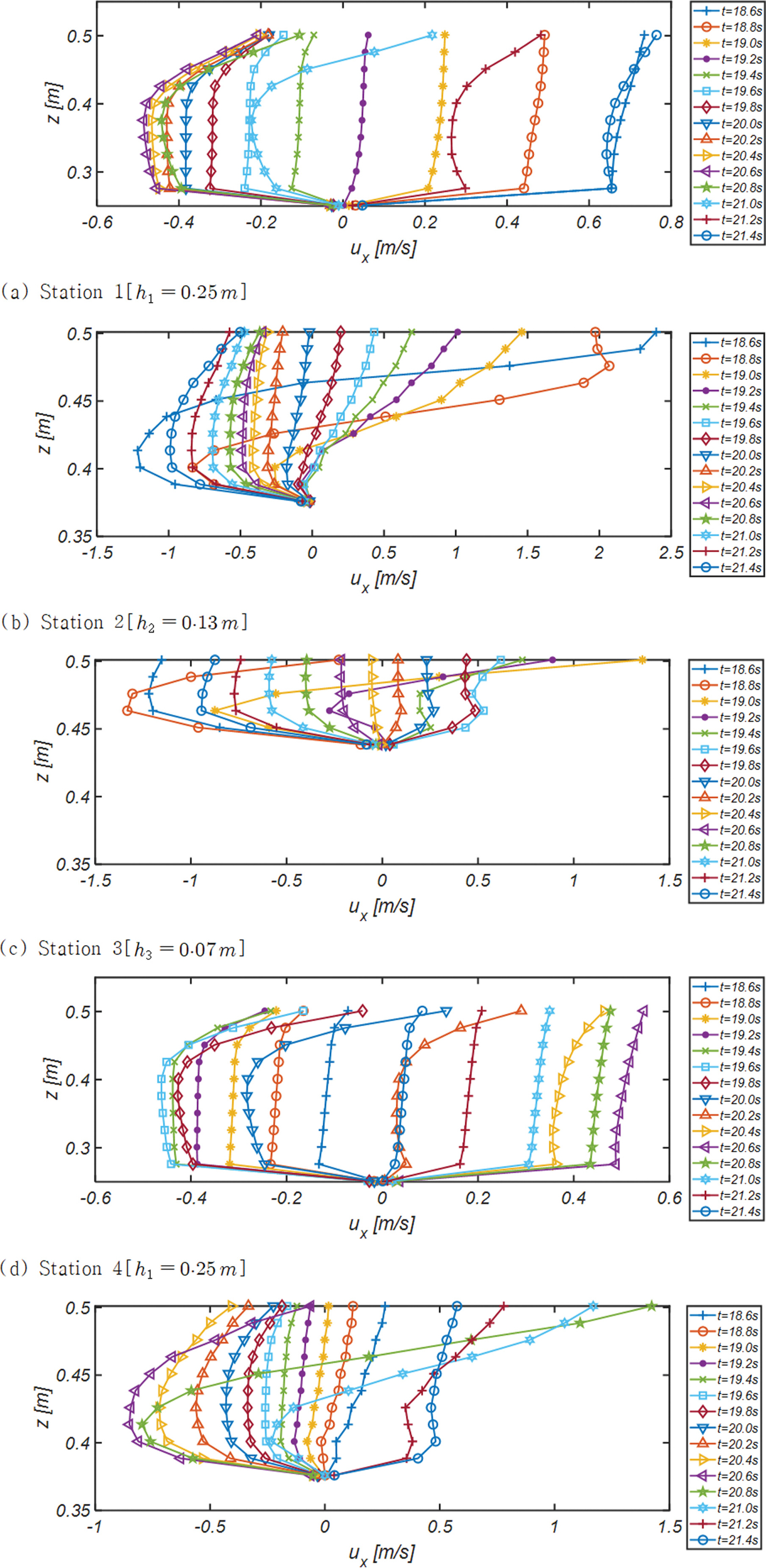
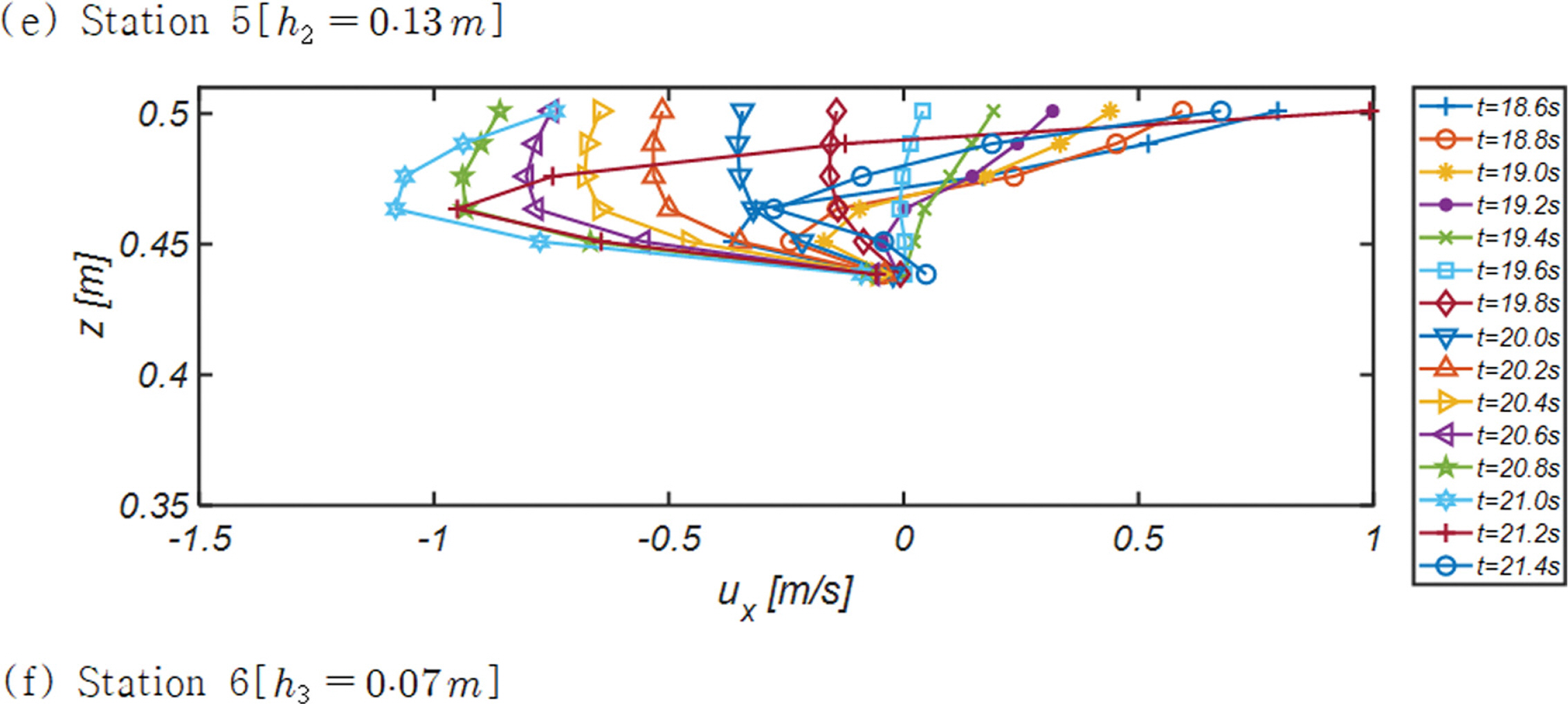
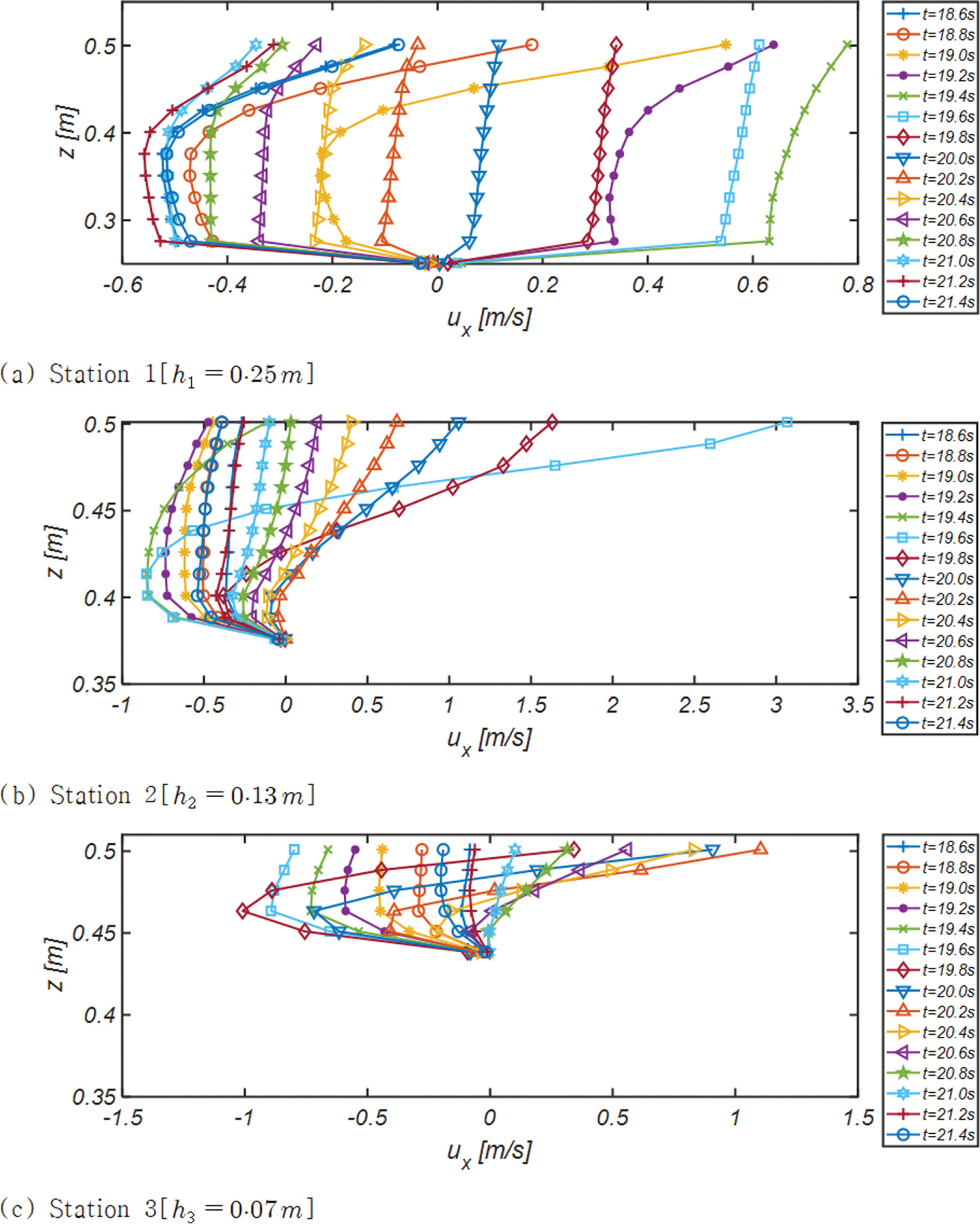
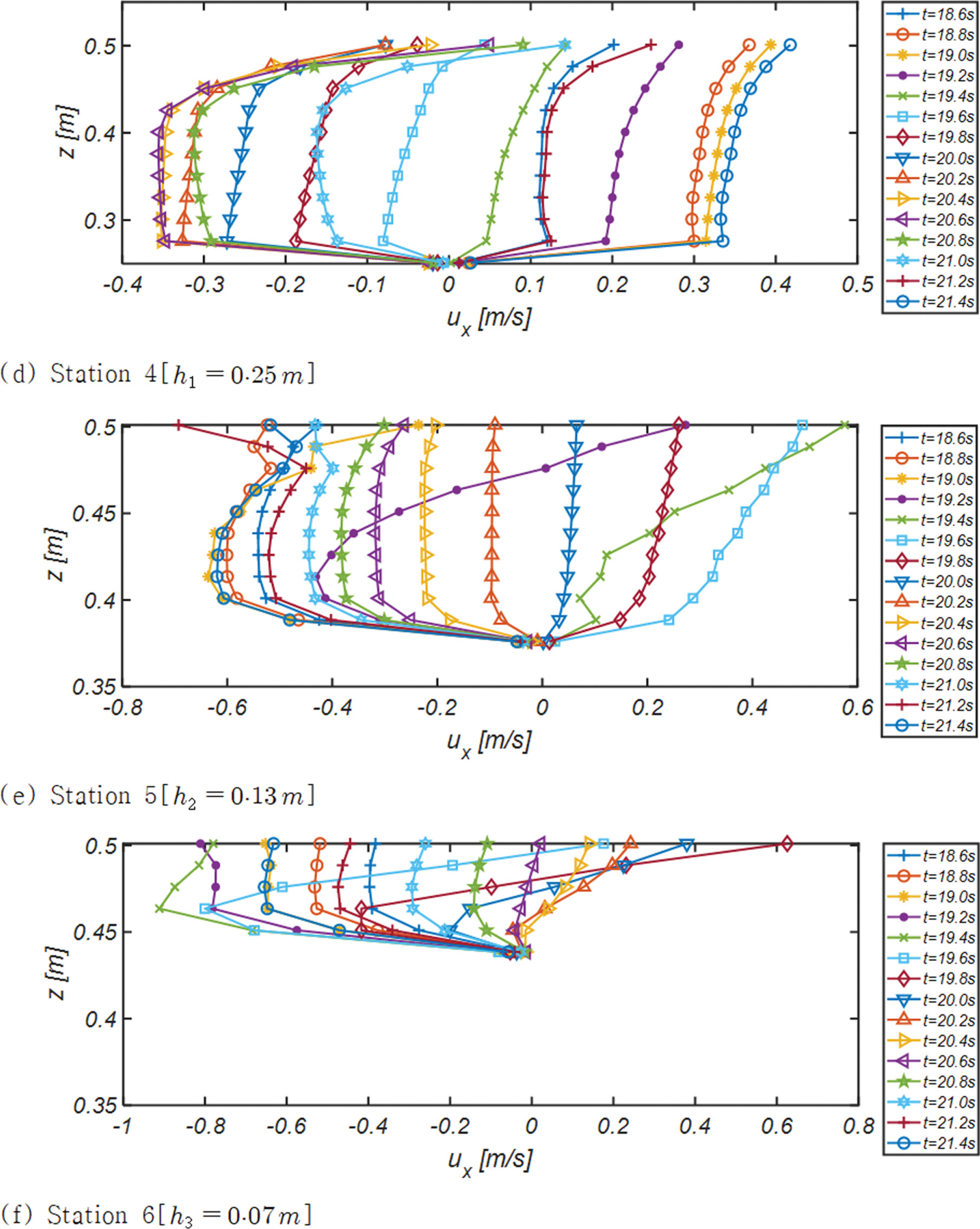
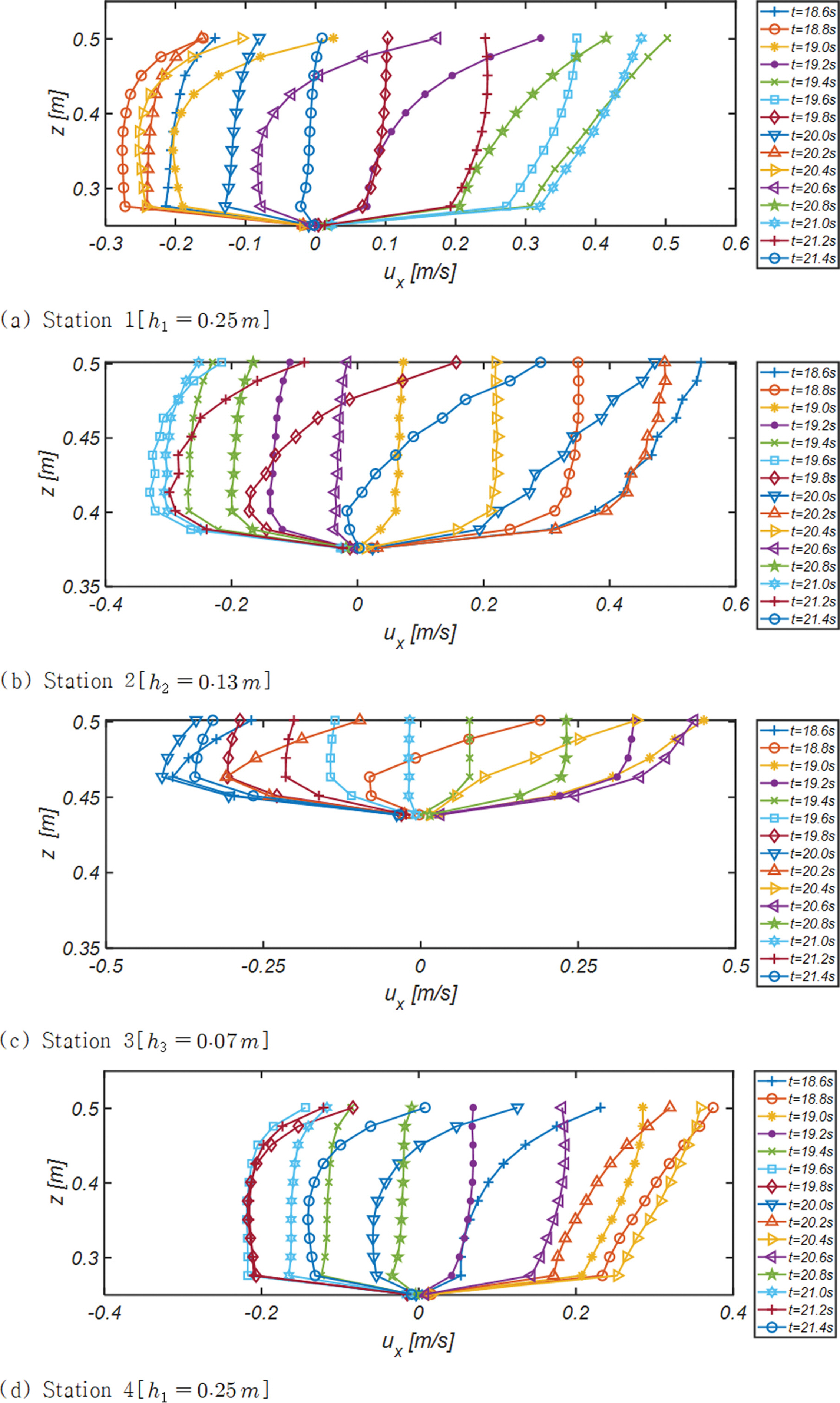
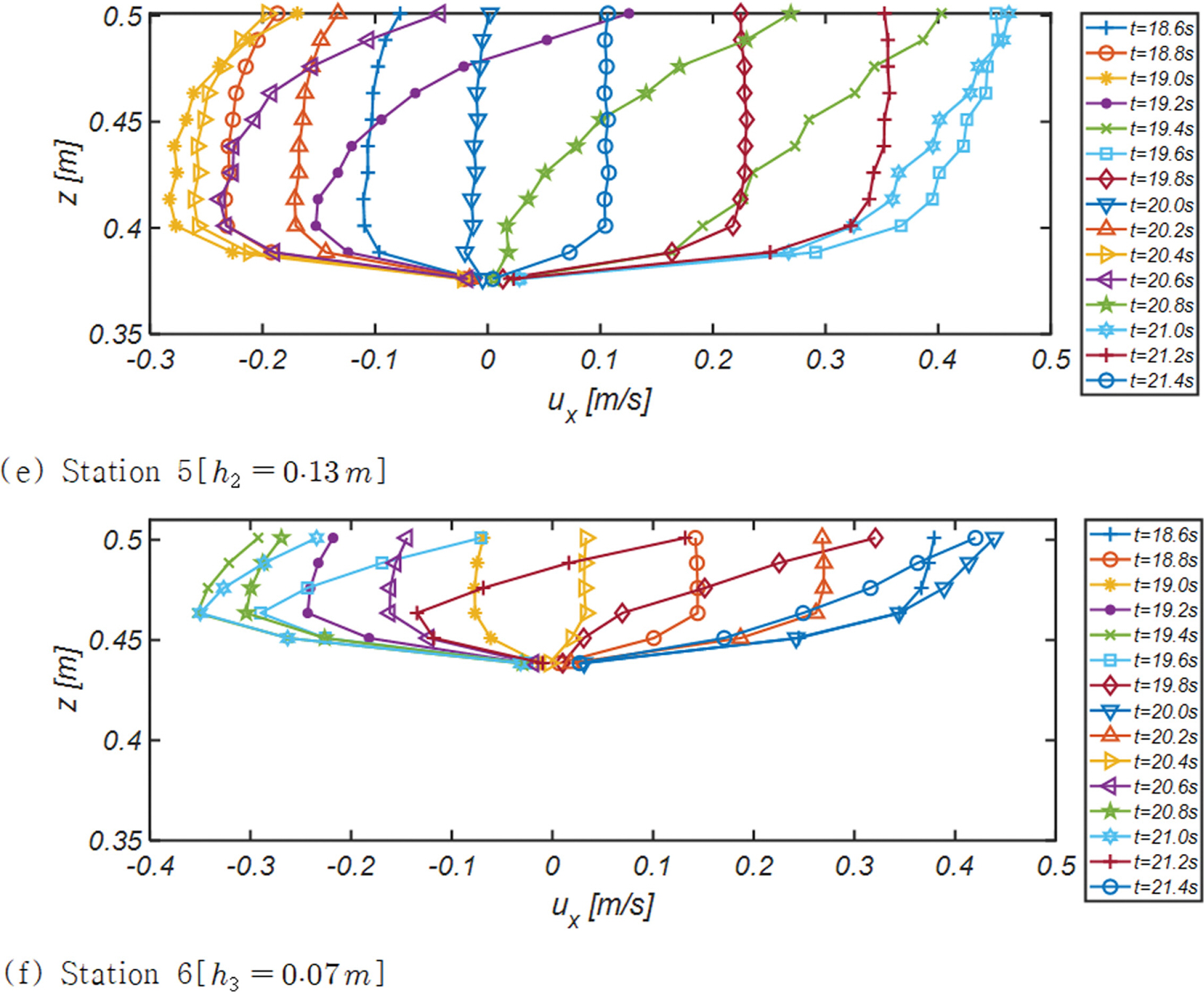
Fig. 7, 8, 9에는 수조중앙을 가로지르는 단면 A - A'[Fig. 3 참조] 천수구역에 거치된 Station 1, 2, 3과 수조중앙을 빗겨간 단면 C - C'[Fig. 3 참조] 천수구역에 거치된 Station 4, 5, 6에서 관측된 해안방향 유속성분 연직분포의 한 주기에 걸친 변화양상을 도시하였다. 한 주기를 총 열 다섯 개의 frame으로 나누어 위상별 유속 변화가 확연하게 드러나도록 구성하였다.
가장 눈에 띄는 추이는 파랑이 집중되는 단면 A - A'에서의 유속이 파랑이 분산되는 단면 C - C'에서의 유속보다 큰 값을 지니며, 주기가 가장 긴 RUN3을 중심으로 각 Station에서 관측되는 특기할 만한 수리현상을 정리하면 다음과 같다:
A. Station 1
I. 천수가 시작되는 초입부에 해당하는 Station1의 경우 해안방향 유속이 먼 바다를 향하는 유속보다 큰 값을 지니나, 지속 시간은 먼 바다 방향흐름이 우월한 전형적인 비선형 파동계의 특징을 찾아볼 수 있다. 또한 유속 구배로 저면 전단응력을 추정하는 경우 해안방향 전단력이 상대적으로 크다는 것을 확인할 수 있다.
II. 후행 파랑이 도달한 t = 21 s의 경우 수면 인근에서의 흐름은 해안을 향하나 그 밖의 수심에서는 [0 < z < 0.45m] 선행 파랑에 의한 back-wash로 먼 바다를 향하는 것을 알 수 있다.
III. 여기서 한 가지 흥미로운 수리현상은 up-rush가 진행 중인 t = 21.2 s의 경우 저면 인근에서의 해안 방향 유속이 중간대역보다 큰 값을 지닌다. 이러한 현상은 중간 대역에서 back-wash는 빠르게 진행되며, 이는 큰 관성력으로 이어진다. 따라서 흐름방향이 해안으로 역전되기 위해서는 많은 힘이 소요되나, 저면 인근의 경우 느린 유속으로 인해 흐름 방향 역전이 비교적 용이하여 발생하는 것으로 판단된다.
IV. 전술한 해석은 경계층 streaming에 대한 Longuet-Higgins (1953)의 해석과는 결을 달리하는 것으로 너울이 우세한 해양환경에서 고파랑에 의해 일시적으로 침식된 자연해빈이 복원되는 과정에서 중요한 기작으로 기능하는 경계층 streaming과 경계층 streaming이 표사이송에 미치는 영향에 대해서는 향후 상당한 논의가 필요해 보인다.
B. Station 2
I. 천수구간 깊숙이 위치한 Station 2에서는 중력에 의해 먼 바다로 회귀하는 back-wash가 충분히 가속되어 상당한 세기의 먼 바다 방향의 흐름이 전 수심에서 관측된다[t = 21.4 s].
II. Up-rush가 정점을 이루는 t=18.6s에서도 해안 방향 흐름은 수면 인근으로 제한되며, 그 밖의 대역에서는 먼 바다 방향의 흐름이 여전히 유지되는 것이 흥미롭다. 후행 파랑이 도달한 t = 18.6 s에서 해안 방향 흐름의 세기는 정점에 이르며 최대 유속은 2.4 m/s로 관측된다.
III. Back-wash시 먼 바다 방향의 최대유속은 약 - 1.25 m/s로 관측되어 해안방향으로의 흐름 비대칭성은 유지되나, 여전히 먼 바다 방향흐름의 지속 시간이 우월하다.
C. Station 3
I. 해안에 인근 한 Station 3에서 중력에 의해 먼 바다로 회귀하는 back-wash는 가속되기 시작하는 것으로 보이며 먼 바다 방향의 최대유속은 약 - 1.4 m/s로 관측되어, 여전히 해안 방향의 최대유속[1.5 m/s, t = 19 s]이 우월한 비대칭성은 유지되는 것으로 보인다.
II. Up-rush가 정점을 이루는 t = 19 s에서도 Station 2에서와 동일하게 해안 방향 흐름은 수면 인근으로 제한되며, 그밖의 대역에서는 먼 바다 방향의 흐름이 여전히 유지된다.
III. 저면 인근에서는 느린 유속과 작은 관성력으로 인해 흐름방향 전환이 비교적 용이하여 t = 19.2 s, t = 19.6 s의 경우 저면 인근 흐름이 중간 대역보다 빠르게 진행되는 것을 확인할 수 있다[A-III, IV 참조].
D. Station 4
I. 전체적으로 파랑 분산으로 인해 유속은 Station 1에서 보다 적은 값을 지니며, 최대유속 기준으로 17% 감속되는 것을 알 수 있다.
II. 단면 A - A'에서의 처오름 정점에서 단면 B - B'와 C - C' 방향으로 나뉘어 먼 바다 방향으로의 흐름에 더해지는 집수효과로 먼 바다를 향하는 흐름과 해안 방향 흐름의 비대칭성은 현저히 감소되는 것을 확인할 수 있다.
III. 저면 인근 흐름이 중간 대역보다 빠르게 진행되는 현상이 t = 20.2 s와 t = 20.4 s에서 확인할 수 있다[A-III 참조].
E. Station 5
I. D-II에서 살펴보았듯 집수효과로 먼 바다를 향하는 흐름과 해안 방향 흐름의 비대칭성은 현저히 감소되는 것을 알 수 있다.
II. 저면 인근 흐름이 중간 대역보다 빠르게 진행되는 현상이 t = 21.0 s와 t = 21.2 s에서 확인할 수 있다[A-III, D-III 참조].
F. Station 6
I. 집수효과로 먼 바다를 향하는 흐름과 해안 방향 흐름의 비대칭성은 현저히 감소되는 것으로 보인다[D-II 참조].
II. 전술한 집수효과로 먼 바다를 향하는 흐름 강도가 해안방향 흐름 강도보다 큰 것을 확인할 수 있다. 이는 해안방향유속이 먼 바다를 향하는 유속보다 큰 비선형 파동계의 일반적인 성정과는 각을 세우는 것으로 집수효과로 파랑이 분산되는 단면에서 b ac k-wash가 지배적인 Synchronous Edge waves가 정확히 모의되었음을 함의한다.
전술한 RUN3에서 관측된 Station 1~6 수리특성은 RUN1, RUN2에서도 유사하게 관측되나, RUN2 Station 5 t = 21 s, 21.2 s에서 관측되는 유속분포가 흥미롭다[Fig. 8(e) 참조]. 중간 수심대역에서 정점에 이르는 back-wash의 일반적인 성정과는 다르게 자유수면 인근에서 back-wash 최대 유속이 발생하였다. Station 5는 파랑이 분산되는 단면으로 전술한 집수효과로 추가로 도입되는 먼 바다를 향하는 흐름에 기인하는 것으로 추정되나, 왜 RUN2에서만 관측되는 지에 대해서는 상당한 논의가 필요해 보이나, 처오름 정점에서 시작되는 먼 바다 방향의 회귀류 생성 주기가 입사파랑 주기에 근접하여 생기는 공진 현상으로 판단된다.
4.3 주기평균 유동계의 수리특성- Under tow, Stokes Drift, Boundary layer streaming
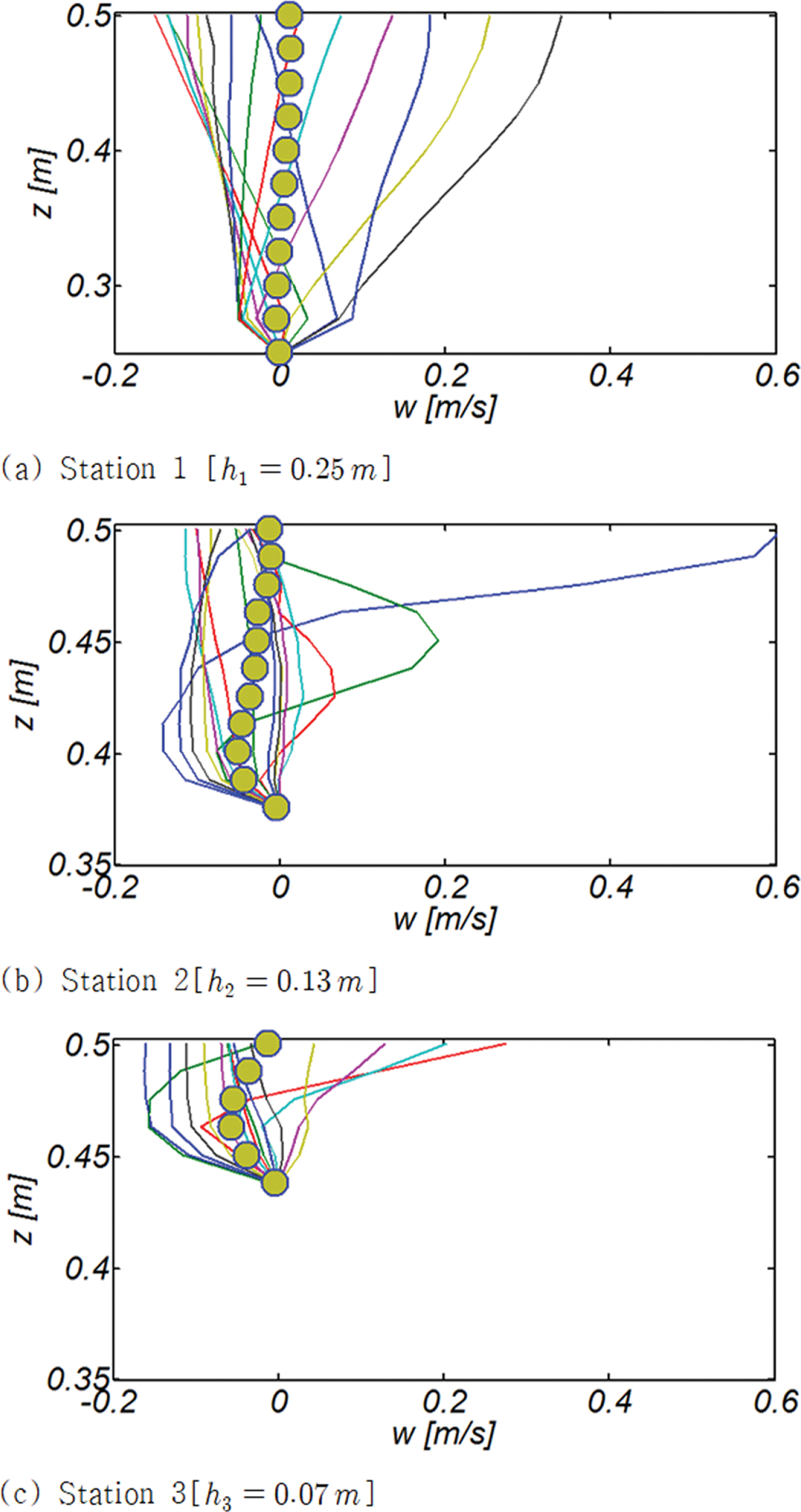
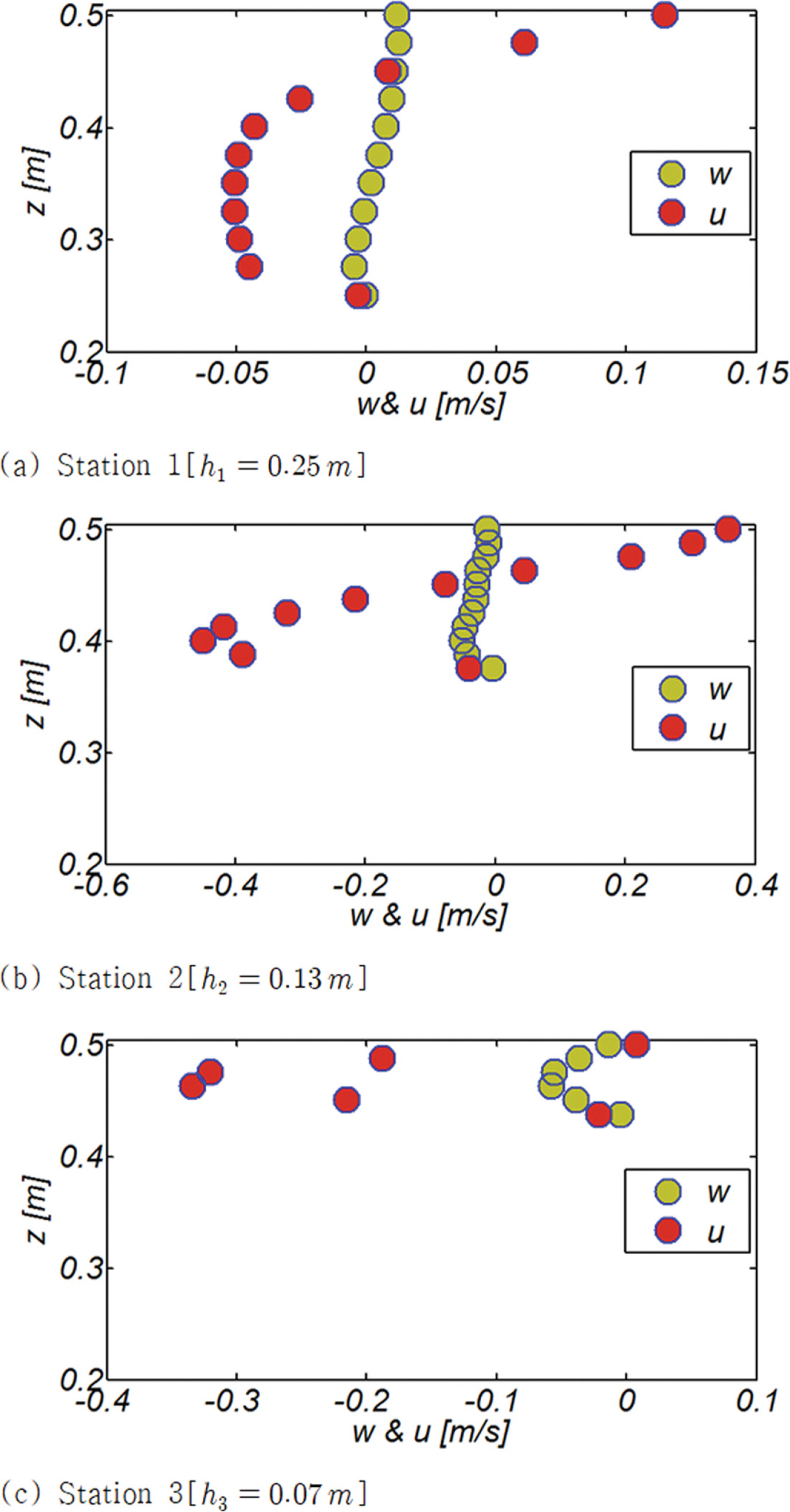
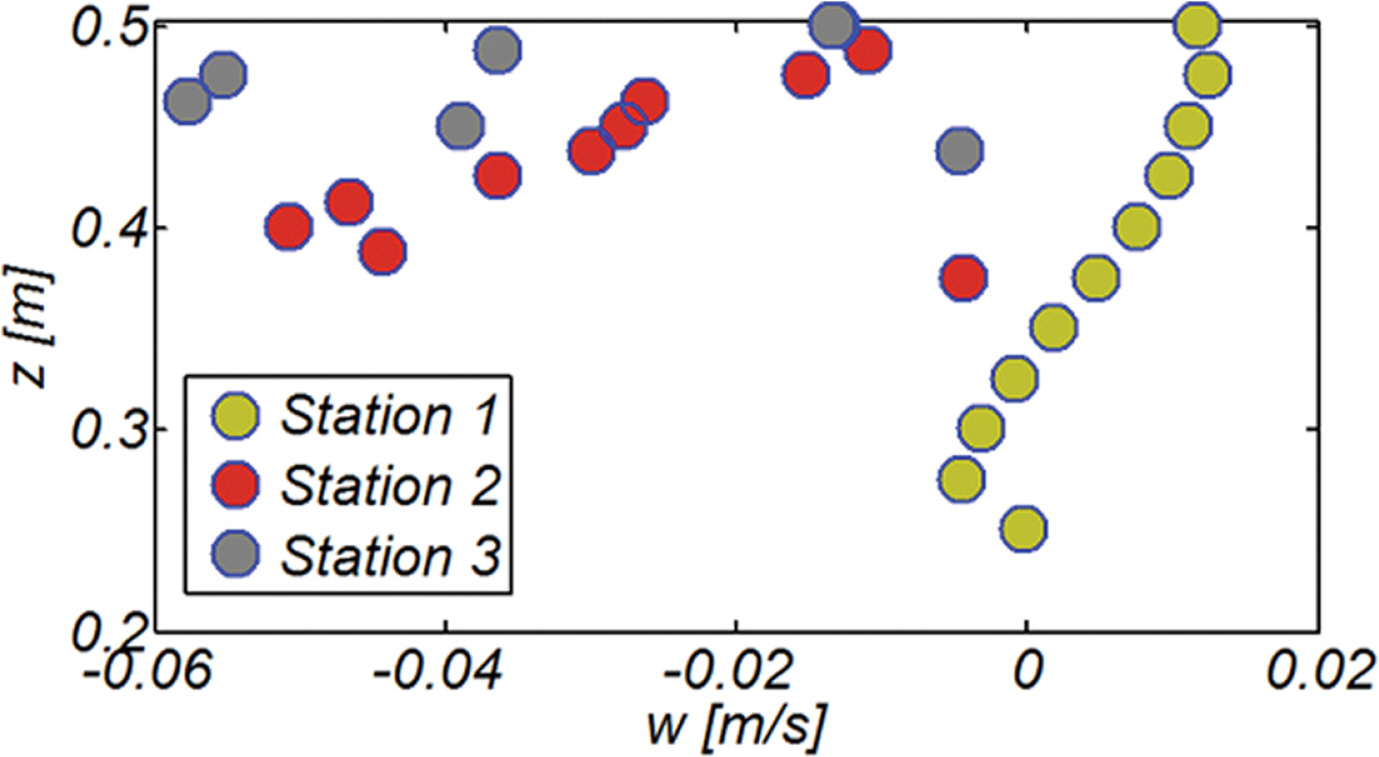
Synchronous Edge waves가 순 해빈표사 이송에 미치는 영향을 살펴보기 위해 수치모의 된 유속을 주기 평균하였다. Fig. 10에는 Station 1, 2, 3에서 관측되는 연직방향 유속의 한 주기에 걸친 변화양상과 주기 평균 유속을 도시하였으며[RUN3], Fig. 11에는 Station 1, 2, 3에서 관측되는 주기 평균 파랑 진행방향 유속과 연직 방향 유속 분포를 함께 도시하였다[RUN3].
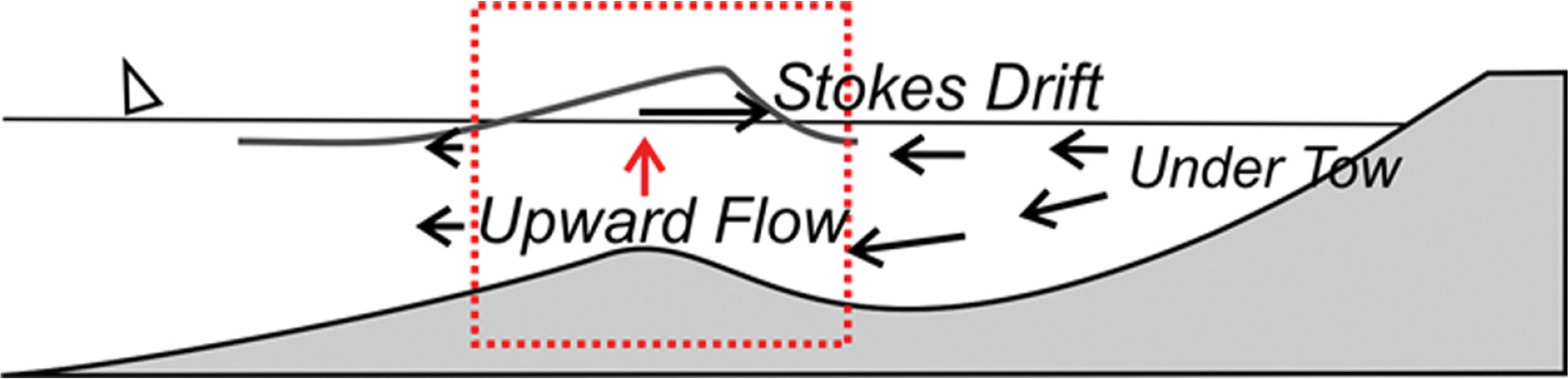
주기 평균된 유동계의 경우 저면 인근에서는 하향하는 연직 유속성분이 우월하며, 이러한 경향은 해안에 근접할수록 증가하며 하향 연직 유속성분이 우월한 수심 대역도 수면 인근까지 확대되는 것을 알 수 있다[Fig. 10, 11. 12 참조]. 해빈표사 이송의 주 기작으로 알려진 Under-tow는 처오름 정점에서 먼 바다 방향으로 회귀되는 흐름의 특성으로 인해 해안에 가장 가까운 Station 3에서는 이미 상당히 가속되어 전수심 대역에서 먼 바다 방향 흐름이 지배적이며, 천수 중간 단계인 Station 2에서는 저면 인근에는 먼 바다 방향 흐름인 Under-tow가 우월하나, 수면 인근에서는 해안 방향 흐름인 Stokes Drift가 지배적인 것으로 모의되었다. 천수 시작 단계인 Station 1에서는 순 흐름 방향은 상당한 수심 대역에서 여전히 먼 바다를 향하나 수심 증가에 따라 그 세기는 - 0.05 m/s 내외로 상당히 약해진 것을 알 수 있으며, 수면 인근에서는 최대 0.12 m/s에 이르는 상당한 세기의 Stokes Drift가 진행되는 것을 알 수 있다. 여기서 한 가지 눈에 띄는 수리현상은 Station 1의 경우 저면 인근을 제외한 상당한 수심대역에서 연직 유속성분이 상향하는 것으로 보인다[Fig. 12 참조]. 이러한 현상은 먼 바다 방향으로 점차 감소하는 undertow로 인해 통제용적으로 순유입 된 질량과 균형을 이루기 위해 생성된 흐름으로 쇄파역에서 관측되는 사주[sand bar]형성에 중요한 역할을 수행하는 것으로 판단된다[Fig. 13 참조].
이상의 논의를 종합하면 너울이 우월한 해양환경에서 경계층 streaming 등으로 해안으로 회귀되는 표사의 이동궤적은 사주 언저리까지는 소류사 형태로 이동되다 사주에서 부유되어 Stokes Drift에 의해 해안까지 이송된다는 추론이 가능해 보인다. 이렇게 해안으로 회귀된 표사는 해안공학 계에 잘 알려진 것처럼 포말 대에서 진행되는 처오름 과정에서 너울이 우월한 해양환경에서 낮아진 지하수위로 인해 발생하는 부분적인 침투로 전빈에 퇴적된다.
5. 결 론
자연해안에서 흔히 관측되는 beach cusp은 일 년에 걸친 해빈 대순환과정을 구성하는 중요한 형태학적 요소라는 점에서 Beach cusp 생성기작으로 알려진 Synchronous Edge wave의 수리특성을 살펴보는 작업은 상당한 공학적 가치를 지닌다. 이러한 시각에서 본 논문에서는 Beach cusp의 생성기작으로 알려진 Synchronous Edge wave의 수리특성을 살펴보기 위한 3D 수치모의를 수행하였다. 수치모의는 OpenFOAM 기반 tool box인 IHFOAM에 기초하여 수행되었으며, 파랑모형은 RANS(Reynolds Averaged Navier-Stokes equation)와 질량 보존식으로 구성하였다. Synchronous Edge waves 형성에 필요한 연안방향으로 파고가 변조되는 short-crested waves는 동일한 주기와 파고를 지니는 두 개의 Cnoidal wave가 전면 해역에서 비스듬히 조우되도록 조파하여 재현하였다.
모의결과 파랑 집중단면에서의 유속이 파랑 분산단면보다 전체적으로 크게 모의되었다. 또한 파랑 집중단면에서는 해안방향 흐름[up-rush]이 먼 바다방향 흐름[back-wash]보다 세기는 우월하나 지속기간은 짧은 비선형 파동계의 일반적인 성정을 지니는 것으로 모의되었다. 이와 더불어 처오름 정점에서 양쪽의 파랑 분산단면으로 흐름이 둘로 나뉘며 약해지는 back-wash로 인해 up-rush 최대유속은 back-wash 최대유속의 두 배 가까이 증가하는 것으로 관측되었다. 이에 비해 파랑분산단면의 경우 파랑 집중단면 처오름 정점에서 양쪽의 분산단면으로 흐름이 나뉘며 발생하는 분산단면에서 집수되는 효과로 인해 해안 인근 수역에서는 먼 바다방향 흐름이 해안방향 흐름보다 우월하게 모의되었다. 또한 천수 중간 수역에서는 해안방향 흐름이 여전히 우세하나 비대칭 정도는 현저하게 감소하였다. 이러한 수리특성은 Synchronous Edge wave의 전형적인 성정으로 수치모의가 성공적으로 이루어진 것으로 판단된다. 이 과정에서 너울이 우월한 해양환경에서 해빈이 느리지만 점진적으로 복원되는 과정에서 주 기작으로 기능하는 경계층 streaming에 대한 새로운 해석도 제시되었다.
수치모의 과정에서 상당 기간 동안 저면 인근 해안방향 유속이 중간 수심대역보다 큰 값을 지니는 것으로 관측되었다. 이러한 현상은 중간 대역에서 빠르게 진행되는 back-wash는 큰 관성력을 지니며, 따라서 흐름방향이 해안방향으로 역전되기 위해서는 많은 힘이 소요되나, 저면 인근의 경우 느린 유속으로 인해 흐름 방향 역전이 비교적 용이하여 발생하는 것으로 판단된다. 이러한 해석은 경계층 streaming에 대한 Longuet-Higgins(1953)의 해석과는 결을 달리하는 것으로 이러한 경계층 streaming 해석이 표사이송에 미치는 영향에 대해서는 향후 상당한 논의가 필요해 보인다. 중간 수심대역에서 정점에 이르는 back-wash의 일반적인 성정과는 다르게 RUN2에서 자유수면 인근에서 최대 back-wash 유속이 발생하는 현상은 파랑 분산되는 단면에서 관측되어 2장에서 다룬 집수효과로 추가로 도입되는 먼 바다를 향하는 흐름에 기인하는 것으로 추정되나, 왜 RUN2에서만 관측되는 지에 대해서는 향 후 상당한 논의가 필요해 보이나, 처오름 정점에서 시작되는 먼 바다 방향의 회귀류 생성 주기가 입사파랑 주기에 근접하여 생기는 공진 현상으로 판단된다.
Synchronous Edge waves가 순 해빈표사 이송에 미치는 영향을 가늠할 수 있는 주기 평균 유동계의 저면 인근에서는 하향하는 연직 유속성분이 우월하며, 이러한 경향은 해안에 근접할수록 증가하며 하향 연직 유속성분이 우월한 수심 대역도 수면 인근까지 확대되는 것으로 모의되었다. 해빈표사이송의 주 기작으로 알려진 Under-tow는 처오름 정점으로부터 먼 바다 방향으로 회귀되는 흐름의 특성으로 인해 해안인근에서는 기 가속되어 전 수심 대역에서 먼 바다 방향 흐름이 지배적이며, 천수 중간단계에서는 저면 인근에는 먼 바다방향 흐름인 Under-tow가 우월하나, 수면 인근에서는 해안 방향 흐름인 Stokes Drift가 지배적인 것으로 드러났다. 이에 반해 천수 시작 단계에서는 순 흐름 방향은 상당한 수심 대역에서 여전히 먼 바다를 향하나 수심 증가에 따라 그 세기는 상당히 약해지며, 수면 인근에서는 상당한 세기의 Stokes Drift가 진행되는 것으로 모의되었다. 주기 평균 유동계에서 가장 눈에 띄는 수리현상은 천수 시작 단계에서 저면 인근을 제외한 상당한 수심대역에서 연직 유속성분이 상향하는 것으로 보인다. 이러한 현상은 먼 바다 방향으로 점진적으로 감소하는 under-tow로 인해 통제용적으로 순유입 된 질량과 균형을 이루기 위해 생성된 흐름으로 쇄파역에서 관측되는 사주[sand bar]형성 주 기작으로 기능하는 것으로 판단된다. 이상의 모의결과를 종합하면 너울이 우월한 해양환경에서 경계층 streaming 등으로 해안으로 회귀되는 표사의 이동궤적은 사주 언저리까지는 소류사 형태로 이동되다 사주에서 부유되어 Stokes Drift에 의해 해안까지 이송된다는 추정이 가능해 보인다. 이렇게 해안으로 회귀된 표사는 해안공학 계에 잘 알려진 것처럼, 포말대에서 진행되는 처오름 과정에서 너울이 우월한 해양환경에서 낮아진 지하수위로 인해 발생하는 부분적인 침투로 전빈에 퇴적된다.