요약해수의 유동 및 염분 변화에 대한 재현성이 검증된 3차원 수치모델을 활용하여 한강 유량에 따른 경기만 염하수로에서의 담수 영향범위를 모의하였다. 염하수로 상류의 입구를 기준으로, 표층에서 28 psu의 염분이 나타나는 지점까지의 거리를 담수가 확산되는 거리로 정의하였으며, 한강으로부터 유출되는 담수 유량을 총 10가지(200~10,000 m3/s)로 구분하여 실험을 구성하였다. 수치모델 결과를 바탕으로, 비선형 회귀분석을 수행하여 유량과 담수 확산 거리에 대한 관계식을 산정하였다. 경기만 염하수로에서의 담수 영향범위는 한강 유량이 증가함에 따라 최소 강화도 남부 해역부터 최대 영흥도 북부 해역까지 확장된다. 유량과 담수 확산 거리는 비례하는 관계로 산정되었으며, 유량이 증가함에 따라 담수 확산 거리의 증가율은 점차적으로 감소하였다. 본 연구에서 산정한 관계식을 바탕으로 특정 시기의 월 평균 한강 유량을 이용하여 염하수로에서의 담수 확산 거리를 추정할 수 있다. 이를 통해, 급격한 담수 유출에 의한 수질 및 생태학적인 피해와 관련된 문제에 대응 및 예측할 수 있을 것으로 기대한다.
AbstractThis study estimates the region of freshwater influence (ROFI) by Han River discharge in the Yeomha channel, Gyeonggi Bay. A 3-D numerical model, which is validated for reproducibility of variation in current velocity and salinity, is applied in Gyeonggi Bay. Distance of freshwater influence (DOFI) is defined as the distance from the entrance of Yeomha channel to the point where surface salinity is 28 psu. Model scenarios were constructed by dividing the Han River discharge into 10 categories (200~10,000 m3/s). The relation equation between freshwater discharge and DOFI was calculated based on performing a non-linear regression analysis. ROFI in Yeomha channel expands from the southern sea area of Ganghwa-do to the northern sea area of Yeongheung-do as the intensity of Han River discharge increases. The discharge and DOFI are a proportional relationship, and the increase rate of DOFI gradually decreases as discharge increases. Based on the relation equation calculated in this study, DOFI in the Yeomha channel can be estimated through the monthly mean Han River discharge. Accordingly, it will be possible to respond and predict problems related to damage to water quality and ecology due to rapid freshwater runoff.
1. 서 론담수 영향범위(Region of freshwater influence, ROFI)는 하천으로부터 유출된 담수가 이류 및 확산 과정을 통해 인근 해역에 영향을 미치는 영역으로 정의된다(Simpson, 1997). 이 영역은 조석, 담수 유출량, 바람, 지형적인 특성, 지구 자전효과 등에 의하여 크기 및 형태가 결정된다(Horner-Devine et al., 2015). 하천으로부터 유출된 담수는 인근 해역에 영양염류, 오염물질, 퇴적물 등을 공급하며, 수괴의 염분을 감소시키는 주된 요인으로 작용한다(Flores et al., 2017). 이로 인하여, 하천이 존재하는 연안 환경에서는 담수 유출에 의한 환경 피해 사례가 지속적으로 제시되어 왔다. 예를 들어, 도시하수의 영향으로 인해 담수와 함께 유출된 PAHs, TBT, 중금속 등의 유해화학물질은 연안생태계의 환경 문제를 야기시키며, 다량의 유기물이 함유된 담수의 유출은 인근 해역에 부영양화 현상을 발생시킨다(Jeong et al., 2017). 또한, 강한 담수 유출량에 의한 염분의 감소는 해양 생물들의 성장과 생존에 악영향을 미친다(Park and Min, 2018). 따라서, 연안 환경에서의 담수 영향범위를 추정하는 것은 수질 및 생태학적 관점에서 중요하다.
대한민국 서해안 중부에 위치한 경기만은 주로 한강, 임진강, 예성강을 통하여 담수 영향범위가 조절되는 해역이다(Fig. 1a). 특히, 3개의 하천 중에서 한강에 의한 담수 유출량이 지배적으로 나타나는 해역이다(Park et al., 2002). 동아시아 몬순 지역에 속하는 한반도의 기후적인 특성에 의하여, 경기만 해역은 담수 유출량의 계절적인 변동성이 뚜렷하게 나타난다. 한강대교의 월 평균 유량을 기반으로, 동계 1~2월의 유량은 약 300 m3/s 이하인 반면에, 하계 7~8월의 유량은 최대 5,500m3/s까지 측정된다. 이에 따라, 하계의 홍수기에는 한강 기원의 영양염류, 오염물질, 퇴적물 등의 육상기원 물질들이 여과 없이 경기만의 외해역까지 운반될 수 있으며, 이는 연안 생태계에 큰 변화를 초래하는 주요 요인으로 작용된다(Lim et al., 2007). 게다가, 대한민국의 산업화, 도시화 등으로 인해 한강으로부터 유출되는 오염 물질의 양은 지속적으로 증가하고 있으며(Kim et al., 2019), 지구온난화에 의한 기후 변화가 가속화됨에 따라 여름철의 강수 현상은 예측하기 어려울 정도로 강도와 빈도수가 증가하고 있다(Kim et al., 2020). 예를 들어, 2020년 8월에 발생한 장기간의 집중호우에 의하여 일 평균 한강 유량이 20,000 m3/s을 초과한 시기가 존재한다. 따라서, 담수 유출 피해와 관련된 문제에 대응 및 예측하기 위하여, 한강 유량을 통해 담수 영향범위를 정량적으로 추정할 수 있는 기술이 필요하다.
경기만 해역에서의 담수 영향범위에 관한 여러가지 연구가 수행되어 왔다(Cho et al., 2008; Jeong et al., 2007; Park, 2004; Yoon and Woo, 2012). 경기만의 총 16개의 정점에 대한 염분 관측 자료를 통해 2000~2002년의 기간 동안의 담수 영향범위를 분석한 Park(2004)의 결과에 따르면, 담수 유출량이 낮은 동계 시기에는 인천 북항 주변의 해역까지 담수가 영향을 미치며, 담수 유출량이 높은 하계 시기에는 팔미도 인근의 해역까지 담수 영향범위가 확장될 수 있다. Yoon and Woo(2012)은 염하수로의 총 9개의 정점에 대한 분기별 염분 관측 자료를 수집하여 1997~2009년의 기간 동안의 염분 분포를 분석하였으며, Park(2004)이 제시한 담수 영향범위를 2차적으로 검증하였다. 하지만, 관측 자료를 기반으로 수행된 선행 연구에서는 공간적인 한계성 및 관측 시간 간격의 불연속성이 존재하기 때문에, 지속적으로 변화하는 담수 유출량의 특성이 반영될 수 없다고 판단된다. 또한, 2020년에는 기록적인 폭우에 의해 기존에 보고되지 않은 한강 유량이 관측되었으나, 이에 따른 담수 영향범위가 어느 영역까지 확장된 지에 대해 보고된 바가 없다.
따라서, 본 연구에서는 경기만 염하수로에서의 유동 및 염분 변화에 대한 검증이 완료된 3차원 수치모델을 활용하여 한강 유량에 따른 담수 영향범위를 추정하였다. 한강으로부터 유출되는 담수 유량을 총 10가지로 구분하여 실험을 구성하였으며, 총 30일의 모의 기간에 대하여 후반 7일 동안의 평균적인 담수 영향범위를 분석하였다. 염하수로의 입구(A)로부터 수심이 가장 깊은 수로를 따라 약 80 km 떨어진 위치(B)까지의 단면을 선정하였으며(A-B in Figs. 1b and c), A-B 단면의 A 지점으로부터의 담수 확산 거리를 계산하였다. 최종적으로, 각 실험의 유량에 따른 담수 확산 거리에 대한 비선형 회귀분석을 수행함으로써, 한강 유량을 통해 담수 확산 거리를 추정할 수 있는 관계식을 제시하였다.
2. 연구 방법2.1 유량 및 염분 자료 수집국가수자원관리종합정보시스템(WAter resource Management Information System, WAMIS)으로부터 2011~2020년 기간에 대한 한강대교의 일 단위 유량 자료를 수집하였다(Fig. 2a). 수집한 유량 자료를 바탕으로, 월별 평균 유량의 10년 치에 대한 최대-최소의 범위 및 평균 값을 계산하였다(Fig. 2b). 최근 10년 간, 동계(1~2월)의 월 평균 유량은 약 90~376 m3/s 의 범위이며, 10년 동안의 평균치는 약 200 m3/s이다. 하계(7~8월)의 월 평균 유량은 약 153~5,500 m3/s의 범위이며, 10년 동안의 평균치는 약 1,500 m3/s이다.
10년 동안의 유량 자료 내에서 홍수기를 선정하기 위하여, 유량이 500 m3/s 이상으로 나타난 26개의 기간들을 1차적으로 선택하였다. 이 기간들 중에서, 평균 유량이 1,000 m3/s 이상으로 나타난 시기를 홍수기로 정의하였다(R1-R11 in Fig. 2a). 10년의 기간 내에서 총 11회의 홍수기가 존재하며, 각 홍수기에 대한 유량 값과 지속 기간을 Table 1에 제시하였다. 11개의 홍수기 중에서 최대 규모의 담수 방류가 나타났던 시기는 R1과 R11이다. R1과 R11 시기의 평균 유량은 각각 3897.6, 4040.4 m3/s로 나타났으며, 지속 기간은 각각 68일, 54일이다. 11개의 홍수기에 대한 평균 유량은 2097.5 m3/s이며, 평균 지속 기간은 약 33.6일로 산정되었다.
해양환경공단(Korea Marine Environment Management Corporation, KOEM)에서 관리하는 해양환경측정망으로부터 A-B 단면에 포함되는 총 6개의 정점(W1-W6 in Fig. 1b)에 대하여 2011~2020년의 기간에 해당하는 표층의 염분 자료를 수집하였다. 해당 염분 자료는 매년 2, 5, 8, 11월에 각각 1회씩 제공되기 때문에 단기적인 시계열 분석에 대하여 한계가 있지만, 염분 분포의 장기적인 변동성을 분석함에 있어서 용이하다(Yoon and Woo, 2012). 수집한 10년치의 염분 자료를 바탕으로, 각 정점의 염분 값의 최대-최소의 범위를 산정하였으며, 2, 5, 8, 11월에 해당하는 평균 염분 값을 각각 계산하였다(Fig. 2c). 전반적으로 W1 정점에서 W6 정점으로 갈수록 염분의 변동성이 감소한다. W1 정점에 대한 염분의 변동성은 약 0~30 psu이며, W6 정점은 약 24~32 psu이다. W1~W6 정점에서 2, 5, 11월의 평균 염분 값은 약 25~31 psu의 범위이며, 상대적으로 담수 유출량이 강한 시기인 8월의 평균 염분 값은 약 21~28 psu의 범위이다. 결과적으로, 염하수로에서의 염분 분포는 한강으로부터 유출되는 담수 유량과 관련이 높으며, 기후적인 특성에 의한 담수 유출량의 계절적인 변동성은 염분 분포의 계절적인 변동성을 야기시키는 주요 메커니즘으로 작용한다(Yoon and Woo, 2012).
2.2 수치모델 구축 및 적용본 연구에서는 Chen et al.(2003)에 의해 개발된 비정규 격자 해양순환 모델인 Finite Volume Coastal Ocean Model (FVCOM)을 사용하였다. FVCOM의 격자는 복잡한 해안선과 지형을 가진 해역에 대해서 효율적으로 계산하기 위해 삼각형 형태로 구성되어 있다(Chen et al., 2008). 또한, 연속방정식, 운동 방정식, 열-염 보존 방정식 등을 포함하는 여러가지 지배방정식에 대한 차분을 통해 격자 내에서 수치적인 계산이 이루어지는 유한 체적법이 사용된다. FVCOM은 매사추세츠 다트머스 대학(University of Massachusetts Dartmouth, UMASSD) 및 우즈홀 해양학 연구팀(Woods Hole Oceanographic Institution, WHOI)에 의해 지속적으로 개발되고 있으며, 세부적인 내용은 Chen et al.(2013)에 상세히 기술되어 있다.
Lee et al.(2021)은 경기만 한강 하구에서의 염 수송에 대한 메커니즘을 분석하기 위해 FVCOM을 사용하여 조위, 유속, 염분에 대한 모델의 검증 및 보정을 수행하였으며, Willmott (1981)에 의해 제시된 predicted skill(Skill)을 계산함으로써 관측 자료에 대한 FVCOM의 재현성을 정량적으로 평가하였다. 해당 모델 결과의 조위, 유속, 염분에 대해서 계산된 Skill은 각각 0.99, 0.95, 0.87 이상으로 나타났으며, 유동 및 염분에 대한 FVCOM의 재현성이 입증되었다. Lee et al.(2021)의 경기만 격자는 한강으로부터 유출되는 담수가 외해 개방경계에 영향을 미치지 않을 정도의 영역으로 구성되어 있다(Fig. 1a). 또한, 외해 개방경계에서는 조위, 유속, 밀도에 대한 완충 작용이 적용된다. 본 연구에서는 담수 입력 조건을 제외하고, 경기만 전체의 격자 구성(Fig. 1) 및 FVCOM의 세부 설정 값들을 Lee et al.(2021)과 동일하게 적용하였다. 수치모델의 담수 입력 조건은 [Section 2.3]에서 언급하였다.
2.3 실험 구성[Section 2.1]에서 제시된 유량 자료를 기반으로, 한강에 대한 수치모델의 담수 입력 조건을 총 10가지로 구분하여 실험을 구성하였다(C1-C10 in Table 2). 최근 10년 동안, 경기만에서 홍수기의 평균 지속 기간은 약 30일이다(Table 1). 이를 기반으로, 30일 평균 한강 유량(Q30)에 따른 담수 확산 거리를 모의하기 위하여, 모든 Case에서의 모의 기간을 총 31일로 설정하였다. 모의 기간 동안 입력된 한강 유량은 일정하게 지속되며, 염분 초기장은 Lee et al.(2021)와 동일하다. 한강대교의 월 평균 유량을 기준으로, C1~C9는 갈수기의 평균 유량(200 m3/s)과 홍수기의 최대 유량(5,500 m3/s)이 포함되도록 구성하였다(Fig. 2b). 담수 유출이 극단적으로 발생하는 경우에 대해서 추가적인 분석을 수행하기 위해 10,000m3/s의 유량이 발생하는 C10을 선정하였다. 임진강과 예성강의 유량은 유역비를 적용하여 각각 한강 유량의 30%, 15%를 입력하였다(Park et al., 2002). 본 연구에서는 총 31일의 모의기간 중에서 대조와 소조 시기가 모두 포함되는 후반 7일 동안의 결과를 활용하여 수치모델 검증 및 결과 분석을 수행하였다. 최종적으로, 각 Case의 Q30에 따른 담수 확산 거리를 계산하였으며, Q30을 통해 담수 확산 거리를 추정할 수 있는 관계식을 산정하였다.
3. 모델 검증경기만 염하수로에서의 담수 확산 거리에 대한 수치모델의 재현성 및 모의 시간의 타당성을 검토하기 위하여, Q30에 따른 W1~W6 정점의 염분 분포에 대한 수치모델의 추가적인 검증이 필요하다. [Section 2.1]에서 제시한 유량과 염분 자료를 토대로, W1~W6 정점에서 관측된 시기 별 염분 값들에 대응하는 Q30을 계산하였다(Table 3). 예를 들어, 2013년 8월 13일에 관측된 W1~W6 정점에서의 염분 값들에 대응하는 Q30은 2013년 7월 14일부터 2013년 8월 12일까지의 기간(30일)의 유량에 대한 평균 값인 3313.1 m3/s이다(Table 3). 하지만, 수집된 염분 자료는 연 4회 제공되는 자료이기 때문에, 대소/소조 및 창조/낙조와 같은 조석 변화에 대한 염분 변동성을 고려할 수 없다. 따라서, 모델 결과에서 나타나는 염분의 조석 변동성 범위 내에 관측 자료가 포함되는지 여부를 통하여 모델 검증을 수행하였다(Fig. 3).
수치모델의 총 31일의 모의 기간 동안 대조와 소조는 각각 3회, 2회씩 발생한다(Fig. 3a). 대표적으로, Q30이 3,000 m3/s인 C6의 실험에 대하여 W3 정점에서의 염분 시계열을 제시하였다(Fig. 3b). 전체 모의 기간 중 대조와 소조 시기를 모두 포함하는 후반 7일 동안의 염분 변동성은 10.6~27.4 psu로 나타났다(Yellow area in Fig. 3b; Pink error bar in Fig. 3e). 이러한 과정을 모든 실험 및 정점에 적용하여 각 Case의 Q30에 따른 염분의 조석 변동성에 대한 최대-최소의 범위를 산정하였으며, 각각의 최댓값을 연결한 선을 Maximum, 최솟값을 연결한 선을 Minimum으로 표시하였다(Sky-blue area in Figs. 3c, d, e, f, g and h). 또한, Table 3에서 제시된 관측 자료 기반의 Q30에 따른 염분 값들을 함께 나타냈다(Red × in Figs. 3c, d, e, f, g and h). 전체 관측 자료의 약 98%가 모델 결과에 대한 염분의 조석 변동성 범위 내에서 재현되었다. 따라서, 한강 유량에 따른 염하수로에서의 담수 확산 거리를 수치모델이 재현함에 있어서, 31일의 모의 기간은 적합하다고 판단된다.
본 연구에서 사용된 수치모델의 담수 유출량은 특정 값이 31일 동안 일정하게 지속된다. 하지만, 실제 현상에서의 담수 유출량은 일정하게 지속되지 않기 때문에, Q30에 따른 염하수로에서의 염분 분포를 수치모델이 재현함에 있어서 일부 오차가 존재할 수 있다. 또한, 수치모델에서 바람에 대한 입력 조건을 구성하지 않았기 때문에, 바람에 의한 표층 염분 분포의 변화는 고려되지 않았다. 이러한 이유로 인하여, 전체 관측 자료의 약 2%는 모델 결과에 대한 염분의 조석 변동성 범위 내에서 재현되지 않았다(E1-E6 in Figs. 3c, d, e, f, g and h).
4. 연구 결과담수 영향범위는 대상 해역의 특성에 따라 다르게 정의된다. 담수 영향범위를 벗어난 지역에서의 염분은 증발 및 강수 등의 요인에 의하여 결정된다(Cho et al., 2008). Connor et al.(2006)은 영국 연안에서 염분이 34 psu 이하로 나타나는 영역을 담수 영향범위로 정의하였다. Cho et al.(2008)은 아산만 연안에서 30 psu의 염분을 기준으로 5%의 변동 범위를 벗어나는 지역을 담수 영향범위로 정의하였다. 이와 같이, 경기만 해역에서도 담수 영향범위를 산정하기 위하여, 영역의 기준이 되는 염분 값에 대한 정의가 필요하다. 국립수산과학원(National Institute of Fisheries Science, NIFS)에서 제공하는 정선해양관측자료로부터 2001~2020년 기간에 해당하는 경기만 외해 지역의 염분 자료를 조사한 결과, 염분의 변동성은 29~32 psu로 나타났다(not shown). 외해 지역에 대한 표층 염분의 감소는 강수에 의한 결과로 판단되며, 이에 따라 담수의 영향이 없는 지역에서의 염분은 강수에 의해 최소29 psu까지 나타날 수 있다. 따라서, 본 연구에서는 한강 유량에 의한 염분의 감소와 강수에 의한 염분의 감소를 구분하기 위해, 염분이 28 psu 이하로 나타나는 영역에 대해서 담수 영향범위로 정의하였다. 이를 토대로, 10가지의 Case에 대해서 모의 기간의 후반 7일 동안의 결과를 활용하여(Yellow area in Figs. 3a and b), 평균적인 담수 영향범위 및 확산 거리를 분석하였다.
4.1 경기만의 담수 영향범위수치모델 결과의 총 10가지의 Case 중, 대표적인 6개의 Case에 대하여 Q30에 따른 경기만 하구의 표층 염분 분포를 제시하였다(Fig. 4). 10,000 m3/s의 극단적인 담수 방류가 발생하는 C10을 제외하고, 경기만의 갈수기를 대표하는 결과는 C1이며, 홍수기를 대표하는 결과는 C3, C5, C6, C9이다. 각 Case 마다 28 psu의 등염분선을 연결하여 담수 영향범위를 표시하였으며(Solid yellow lines in Fig. 4), 경기만의 대표적인 섬 6개(교동도, 석모도, 강화도, 영종도, 무의도, 영흥도)와 항구 2개(북항, 남항)의 위치를 기준으로 담수 영향범위를 분석하였다.
경기만 하구에서 한강 및 임진강으로부터 유출된 담수는 강화도 북부 수로와 염하수로를 통해 각각 85%, 15%의 비율로 유출된다(Red arrow in Fig. 4a; Lee et al., 2021). Q30이 200 m3/s인 C1의 경우, 강화도 북부 수로를 통해 유출된 담수는 석모도 인근 해역까지 확장되며, 염하수로를 통해 유출된 담수는 강화도와 영종도 사이의 해역까지 확장된다(Fig. 4a). Q30이 1,000 m3/s 이상으로 증가되면, 강화도 북부 수로와 염하수로를 통해 유출된 담수는 강화도 남서부 해역에서 서로 만나게 되며(White arrow in Fig. 4b), 인천 북항 인근의 해역까지 담수가 영향을 미치게 된다(NP in Fig. 4b). 담수 영향범위가 인천 남항까지 확장되기 위한 Q30은 2,000m3/s로 나타났으며(SP in Fig. 4c), 이 경우에는 팔미도 인근 해역까지 담수가 확장된다(Green triangle in Fig. 4c). Q30이 3,000 m3/s 이상으로 증가되면, 무의도 인근 해역까지 담수가 영향을 미친다(Figs. 4d, e and f). 또한, Q30이 3,000m3/s 이상인 경우에 대해서 담수 영향범위가 확장되는 비율은 급격하게 감소한다. 10,000 m3/s의 극단적인 담수 방류가 발생하는 C10의 경우, 담수 영향범위는 영흥도 인근 해역까지 확장된다(Fig. 4f). 위의 내용을 종합하면, 갈수기에 경기만 염하수로에서의 담수 영향범위는 강화도 남부 및 영종도 북부해역에서 균형을 이루어 분포한다. 하지만, 홍수기에는 담수 유출량의 세기에 따라 담수가 확산되는 범위는 유동적으로 변화하며, 최대 무의도 남부 및 영흥도 북부 해역까지 확장될 수 있다.
4.2 유량과 담수 확산 거리의 관계식수치모델 결과의 총 10가지의 Case에 대하여, A-B 단면(Fig. 1c)에서의 A 지점으로부터 표층에서 28 psu의 염분이 나타나는 지점까지의 거리(D28)를 계산하여 각 Case 별로 담수 확산 거리를 종합하였다(C1-C10 in Fig. 5a). 또한, [Section 4.1]에서 제시된 경기만 하구에서의 담수 영향범위를 각 Case 별로 종합하여 표시하였다(Fig. 5b). Q30이 200 m3/s인 C1에서의 D28은 약 26.42 km이며, W1과 W2 정점 사이에 위치한다(C1 in Fig. 5a). Q30이 1,000 m3/s인 C3에서의 D28은 약 42.97 km이며, W5 정점 부근에 위치한다(C3 in Fig. 5a). Q30이 2,000 m3/s 이상으로 나타나는 C5~C10의 경우, D28은 항상 W6 정점 이후에 위치하며, C10에서 최대 65.84 km까지 증가한다(C5-C10 in Fig. 5a).
유량과 담수 확산 거리의 상관관계를 파악하기 위하여, A-B 단면에서의 Q30와 D28에 대한 단순 비선형 회귀분석을 수행하였다(Fig. 5c). 각 Case에 대한 D28은 전체 모의 기간에서 후반 7일 동안의 평균적인 확산 거리이기 때문에, 조석에 의해 변동하는 D28의 최대-최소의 범위를 함께 표시하였다(Yellow area in Fig. 5c). Q30와 D28의 관계에 대한 비선형 회귀분석을 통해 산정된 관계식은 식(1)과 같다.
산정된 관계식으로부터 D28은 Q-1/8와 관계가 있는 것으로 나타났으며, 관계식의 결정계수(R2)는 0.98로 산정되었다. 관계식에서 Q-1/8의 계수는 -206.25이며, 관계식의 상수는 130.63이다. Q30와 D28은 비례하는 관계이며, 관계식의 기울기는 감소하는 형태이다.
Q30이 200~1,000 m3/s인 구간에서의 D28은 약 24~44 km이며, Q30이 1,000~6,000 m3/s인 구간에서의 D28은 약 44~61 km이다(Fig. 5c). Q30이 200~1,000 m3/s인 구간에서의 D28의 증가율은 Q30이 1,000~6,000 m3/s인 구간보다 약 7배 이상 높게 나타났다. 결과적으로, 경기만 염하수로에서 Q30이 1,000 m3/s 이하인 경우에 담수 확산 거리의 증가율이 높으며, Q30이 1,000 m3/s 이상인 구간에서는 담수 확산 거리의 증가율이 감소한다.
Q30이 6,000~10,000 m3/s인 구간에서의 D28은 약 61~65 km이다(Fig. 5c). 또한, D28의 증가율은 Q30이 1,000~6,000 m3/s인 구간의 약 0.4배로 나타났다. 하지만, [Section 2.1]에서 제시된 한강대교의 유량 자료를 기준으로, Q30이 10,000 m3/s을 초과한 사례는 존재하지 않는다. 실제로, 경기만의 Q30은 약 90~5,500 m3/s의 범위에서 변화하며, 이를 식(1)에 대입하면 약 13~60 km의 D28이 계산된다. 따라서, 현재까지 측정된 유량 자료를 기준으로, 경기만 염하수로에서의 담수 확산 거리는 최대 60 km(영흥도 북부 해역)까지 나타날 수 있다.
5. 논 의본 연구에서 산정한 관계식에서 담수 확산 거리의 기준 염분은 28 psu이다. 하지만, 수질 및 생태 분야 등의 여러 관점에 따라 담수 확산 거리의 정의는 다를 수 있기 때문에, 기준 염분을 확장할 필요가 있다. 따라서, 기준 염분의 영역을 17~31 psu로 확장하여 각각의 기준 염분에 대한 Q30와 Dn의 관계식을 모두 산정하였다(Fig. 6).
n은 기준 염분을 의미하며, 17~31 psu의 값을 나타낸다. Dn은 A-B 단면에서 A로부터 n psu가 나타나는 지점까지의 거리이다. n이 16 psu 이하인 경우, 담수 확산 거리가 A 지점보다 상류에 위치할 수 있기 때문에, 관계식 산정의 대상에서 제외되었다. 또한, n이 32 psu 이상인 경우에 대해서는 수치모델의 외해 개방경계에 입력된 염분 값과 근사하기 때문에, 마찬가지로 관계식 산정의 대상에서 제외되었다. 모든 관계식에 대하여 Q-1/8의 계수를 HA, 관계식의 상수를 HB라고 하면, Dn은 식(2)와 같이 표현된다.
Q30와 Dn에 대한 모든 관계식의 형태는 Fig. 5c와 유사하며, n이 증가할수록 Dn의 값은 그래프의 형태가 유지된 상태로 점점 증가한다(Fig. 6). Q30와 Dn의 관계식에 대한 HA와 HB의 값을 Table 4에 제시하였다. 관계식의 R2는 n이 20~27 psu인 구간에서 0.97로 나타났으며, 그 외의 구간에서는 0.98이상으로 나타났다.
Q30, n, Dn의 관계성을 파악하기 위하여, Q30와 n을 독립 변수로 지정하여 다중 비선형 회귀분석을 수행하였다. 산정된 관계식의 형태는 식(3a)와 같으며, Dn은 Q-1/8와 n3.7에 대하여 높은 관계성이 나타났다. Q-1/8의 계수를 MA, n3.7의 계수를 MB, 관계식의 상수를 MC라고 하였을 때, 계산된 값은 식(3b, c, d)와 같다.
C1~C10에서 각각 계산된 Dn과 식(3a)의 곡면 그림을 비교한 결과, R2는 0.98로 산정되었다(Fig. 7). 따라서, 30일 평균 한강 유량 값과 기준 염분 값을 식(3a)에 대입하면, 사용자가 선정한 기준 염분 값에 대한 경기만 염하수로에서의 담수 확산 거리를 추정할 수 있다. 예를 들어, 기준 염분을 26 psu로 선정하였을 때 특정 시기의 30일 평균 한강 유량이 1,000 m3/s 라고 하면, 염하수로에서의 담수 확산 거리(D26)는 약 38.35 km로 계산되며 W4와 W5 정점 사이(남항 인근 해역)에 위치한다.
본 연구에서 산정한 유량과 담수 확산 거리에 대한 관계식의 형태는 기울기가 점차적으로 감소하는 형태이다. 이는 조석과 담수의 균형에 의하여 최대로 확장될 수 있는 담수 영향범위가 제한됨을 의미한다. 실제 발생한 사례는 아니지만, Q30이 10,000 m3/s을 초과하더라도 담수 확산 거리의 변동성은 거의 없을 것으로 판단된다. 따라서, 경기만 염하수로에서의 담수 확산 거리는 최대 65 km 이내(영흥도 서부 해역)로 제한된다.
선행 연구에서 제시된 경기만에서의 담수 영향범위는 최대 팔미도 해역이다(Park, 2004; Yoon and Woo, 2012). Yoon and Woo(2012)은 1974~2009년의 기간에 해당하는 36년치의 장기적인 유량 자료를 평균하여 2, 5, 8, 11월의 평균 담수 유출량을 계산하였다. 8월 평균 담수 유출량은 1,478 m3/s로 산정되었으며, 이 값과 염분 관측 자료를 토대로 경기만의 담수 영향범위는 최대 팔미도 해역이라고 추정하였다. 식(1)의 Q30에 1,478 m3/s을 대입하면 약 48 km로 계산되며, 팔미도 해역과 근접한 위치이다. 하지만, 본 연구의 수치모델 시나리오 중, 월 평균 유량이 3,000 m3/s 이상인 시나리오(C6~C10)에서 계산된 담수 영향범위는 팔미도 해역보다 더 넓은 영역까지 확장되었다(Figs. 4d, e and f). 실제로, 한강 유량은 매년 홍수기 마다 지속적으로 변화하는 값이며, 월 평균 유량을 기준으로 최대 5,500 m3/s까지 증가된 시기가 존재한다(Fig. 2b). 이 시기에 염하수로에서의 담수 확산 거리는 식(1)을 기준으로, A-B 단면에서 약 60 km로 계산되며, 위치는 영흥도 북부 인근의 해역에 해당한다. 따라서, 염하수로에서의 담수 확산 거리를 추정하기 위하여, 연 단위 수준에 대한 유량의 장기적인 특성보다 월 단위 수준의 단기적인 특성을 고려해야 한다.
6. 결 론3차원 수치모델을 활용하여 한강 유량을 통해 경기만 염하수로에서의 담수 영향범위를 추정하였다. 한강으로부터 유출되는 담수 유량을 총 10가지로 구분하여 실험을 구성하였으며, 표층의 염분이 28 psu 이하로 나타나는 해역을 담수 영향범위로 정의하였다. 각 실험마다 경기만 해역에서의 공간적인 담수 영향범위를 분석하였으며, 염하수로의 A-B 단면에 대한 수평적인 담수 확산 거리를 정량적으로 계산하였다. 최종적으로, 비선형 회귀분석을 통해 한강 유량과 담수 확산 거리의 관계식을 산정하였다. 본 연구의 결과를 요약하면 다음과 같이 정리된다.
1) 경기만에서의 담수 영향범위는 한강 유량에 따라서 유동적으로 변화한다. 월 평균 한강 유량이 200 m3/s 이하인 갈수기에는 최대 강화도 남부 해역까지 담수가 영향을 미친다. 홍수기에는 월 평균 한강 유량이 1,000~5,500 m3/s의 범위에서 불규칙적으로 나타나며, 담수 영향 범위는 인천 북항 해역부터 최대 영흥도 북부 해역까지 확장된다.
2) 유량과 담수 확산 거리는 서로 비례하는 관계이며, 유량이 증가함에 따라 담수 확산 거리의 증가율은 점차적으로 감소한다. 이는 유량의 증가와 상관없이, 조석과 담수의 균형에 의하여 최대로 확장될 수 있는 담수 영향범위가 제한됨을 의미한다. 따라서, 월 평균 유량이 10,000 m3/s을 초과하더라도 경기만 염하수로에서의 담수 영향범위는 최대 영흥도 서부 해역 이내로 제한된다.
3) 경기만 해역에서의 담수 영향 범위는 유량의 단기적인 특성에 민감한 변화를 보였다. 선행 연구에서는 36년치의 장기적인 유량 자료에 대한 평균치를 토대로 분석하였기 때문에, 담수 영향 범위가 과소 산정이 되었다. 하지만, 본 연구에서 월 평균 유량을 기반으로 분석한 담수 영향범위는 선행 연구에서 제시된 팔미도 해역보다 더 넓은 영역까지 확장된다. 따라서, 정확한 담수 영향범위를 분석하기 위해 유량의 단기적인 특성을 고려해야 한다.
본 연구에서 산정한 관계식을 기반으로, 특정 시기의 월 평균 한강 유량을 이용하여 염하수로에서의 담수 확산 거리를 추정할 수 있다. 이를 통해, 담수 확산에 의한 수질 및 생태학적 피해가 발생할 수 있는 지역들을 한강 유량에 따라 분류할 수 있으며, 홍수기의 급격한 담수 유출에 따른 막대한 피해에 대응할 수 있을 것으로 기대한다. 하지만, 본 수치모델의 결과는 대조/소조 및 고조/저조가 포함된 7일 동안의 평균적인 담수 확산 거리이기 때문에, 조석에 따라 수 시간~수일 단위로 변화하는 담수 확산 거리의 변동성이 고려되지 않았다. 또한, 실제로 특정 담수 유출량이 일정한 값으로 30일 동안 지속되는 경우는 존재하지 않기 때문에, 관계식의 결과에 대하여 오차가 존재할 수 있다. 따라서, 정확한 담수 확산 거리를 산정하기 위해, 앞서 제시한 한계점들을 단계적으로 고려함으로써 관계식을 확장할 수 있는 연구를 지속적으로 수행할 필요가 있다.
감사의 글이 논문은 2021년도 정부(과학기술정보통신부)의 재원으로 정보통신기획평가원의 지원을 받아 수행된 연구임(2020-0-01389, 인공지능융합연구센터지원(인하대학교)). 이 논문은 2021년 해양수산부 재원으로 해양수산과학기술진흥원의 지원을 받아 수행된 연구임(경기씨그랜트).
Figure 1.Map of the Gyeonggi Bay and the computational grid for numerical modeling (a), study area (b), and depth variation along A-B line (c), showing six stations W1-W6 for surface salinity data from KOEM (blue circles). 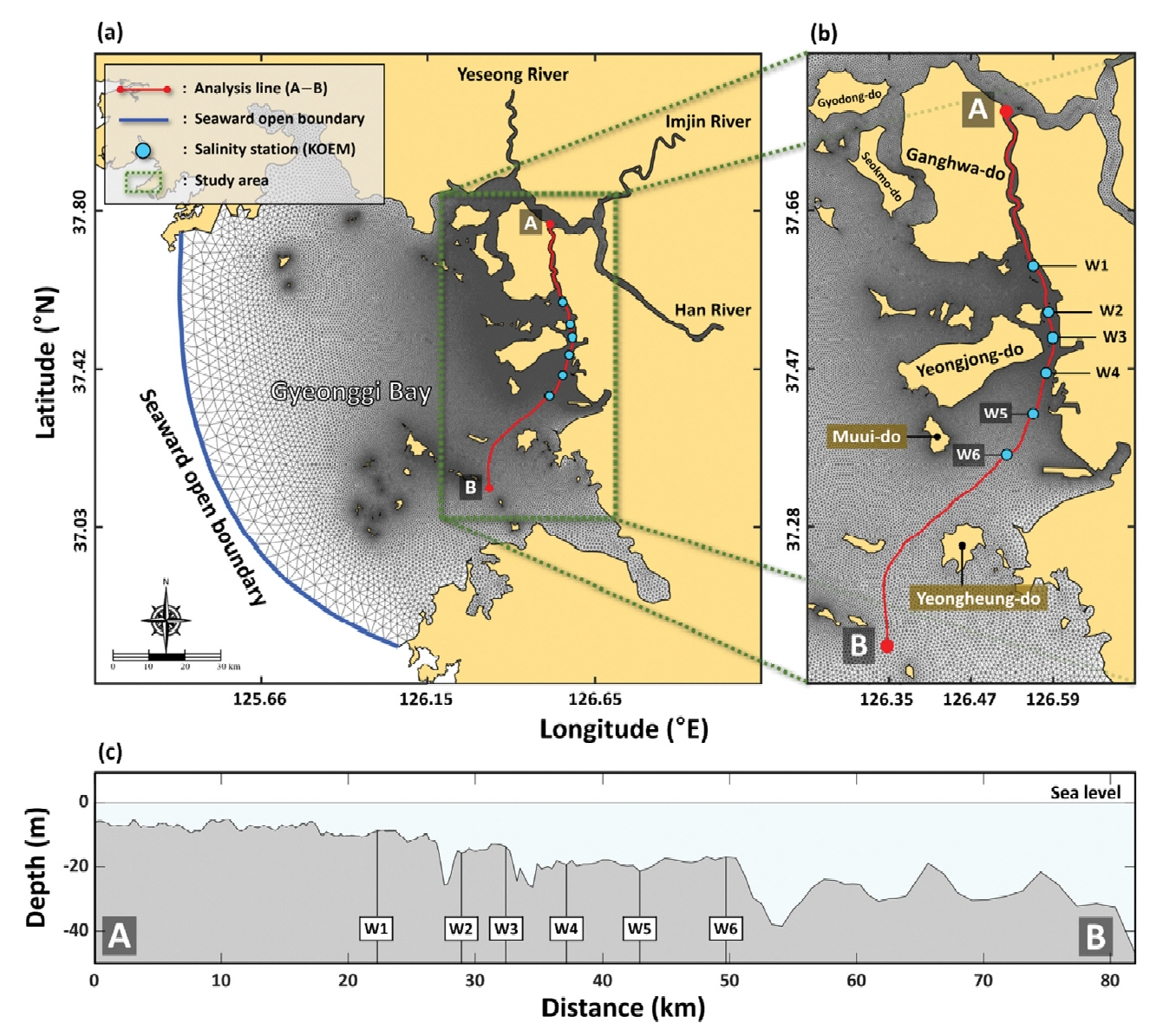
Figure 2.Analysis for river discharge and salinity data: (a) daily mean freshwater discharge at Han River over 2011~2020, showing 11 wet seasons R1-R11, (b) monthly mean freshwater discharge at Han River averaged over 2011~2020, (c) decadal mean salinity data for February (Red line), May (Yellow line), August (Green line), and November (Blue line) at W1-W6 over 2011~2020. The error bar in (b)
and (c) means the maximum-minimum range for 10 years. 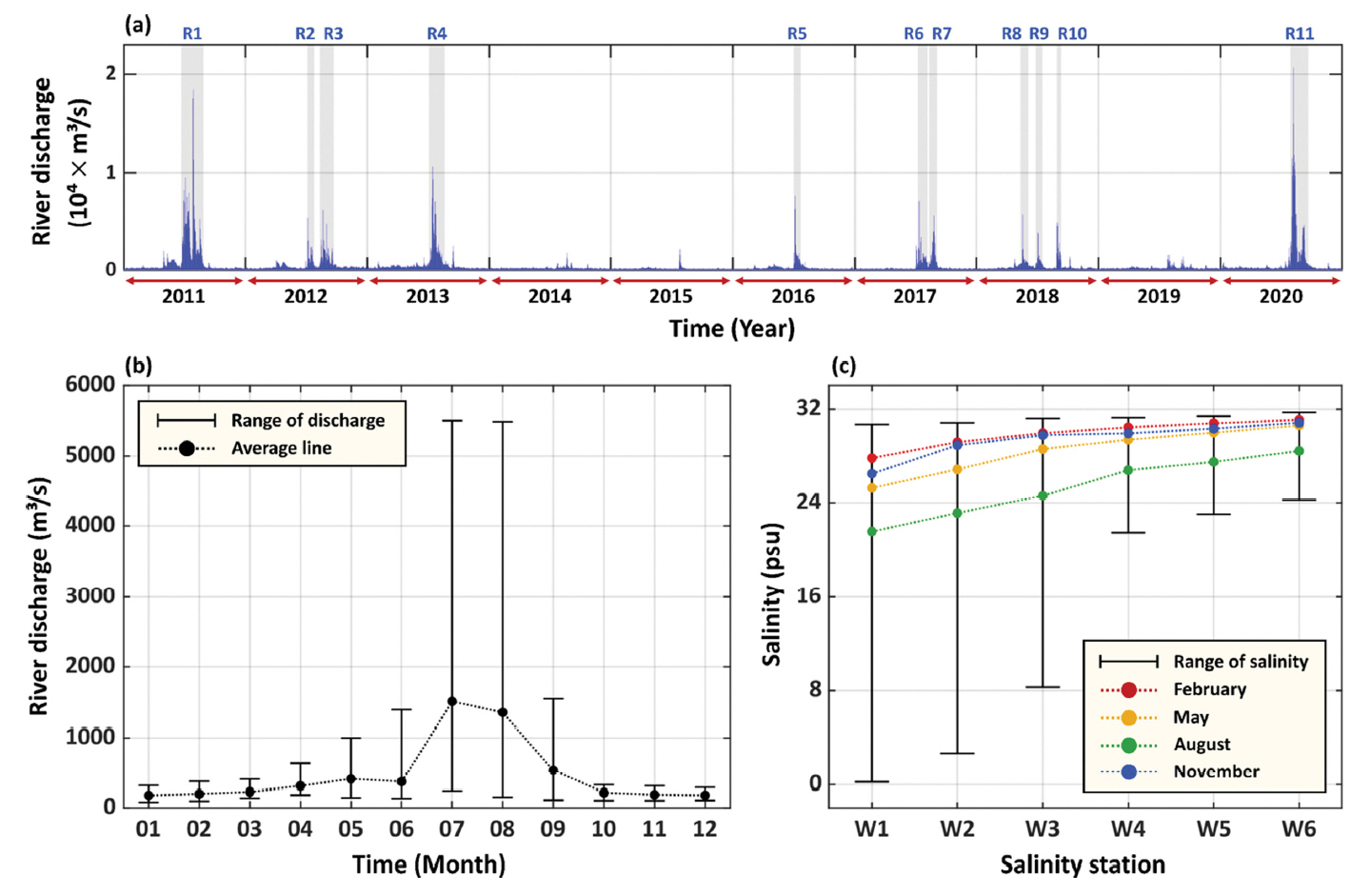
Figure 3.Model validation for salinity in W1-W6: (a) time series of tide level for 31 days simulation period in W3. (b) time series of surface salinity in W3 for case number C6. (c-h) comparison of model results and observation data for surface salinity according to Q30 in W1-W6. The red × denotes the observed salinity given in Table 3, and the error bar is a maximum-minimum range of modeled salinity for tide variation during days 24~30 (Yellow area in (a) and (b)). 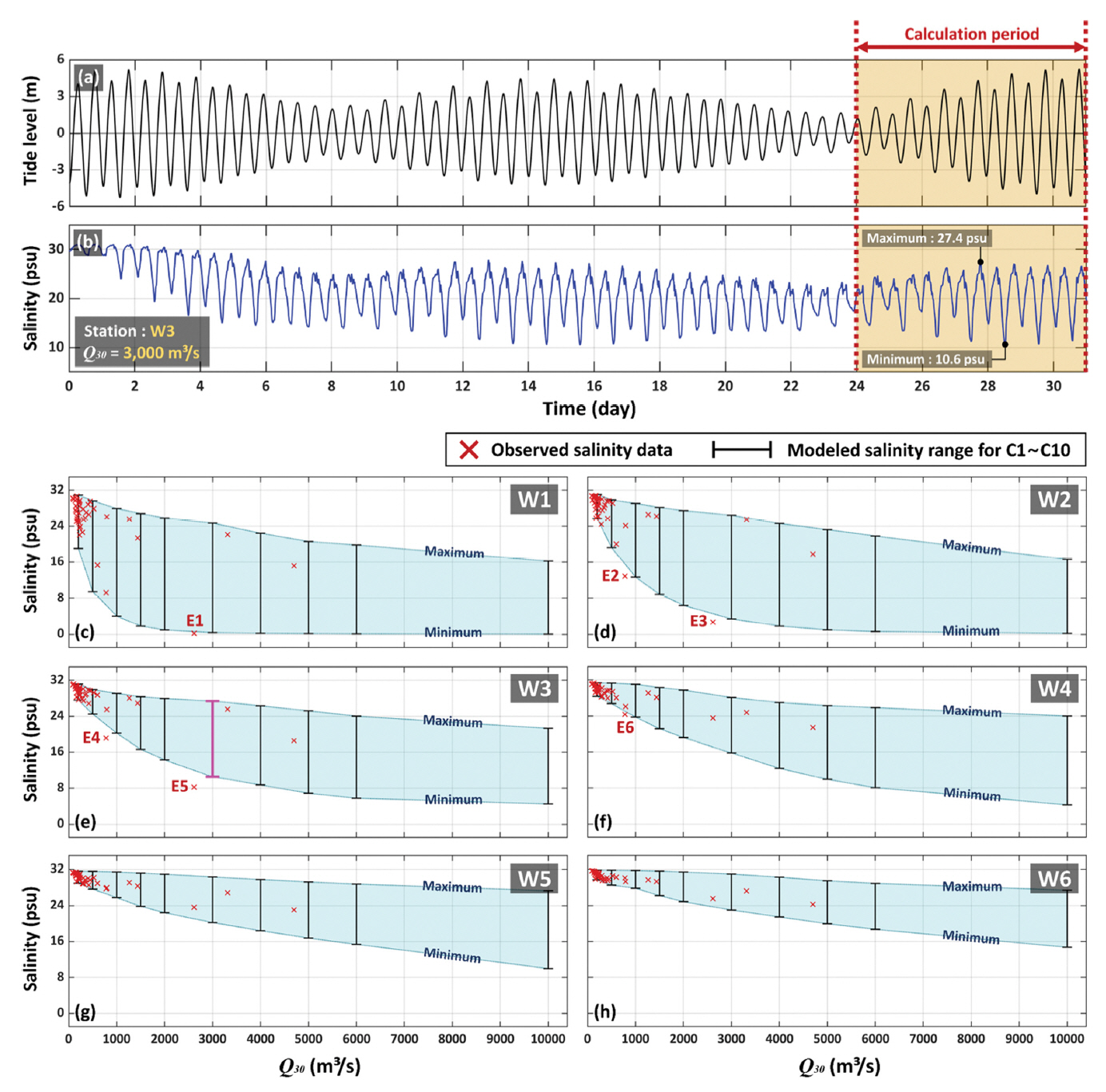
Figure 4.Surface salinity distribution in Gyeonggi Bay for results of six numerical simulations (Case numbers C1, C3, C5, C6, C9, and C10). The solid yellow lines represent isohaline of 28 psu. The results of all scenarios are mean salinity distribution during days 24~30 (see the yellow area in Figs. 3a and b). 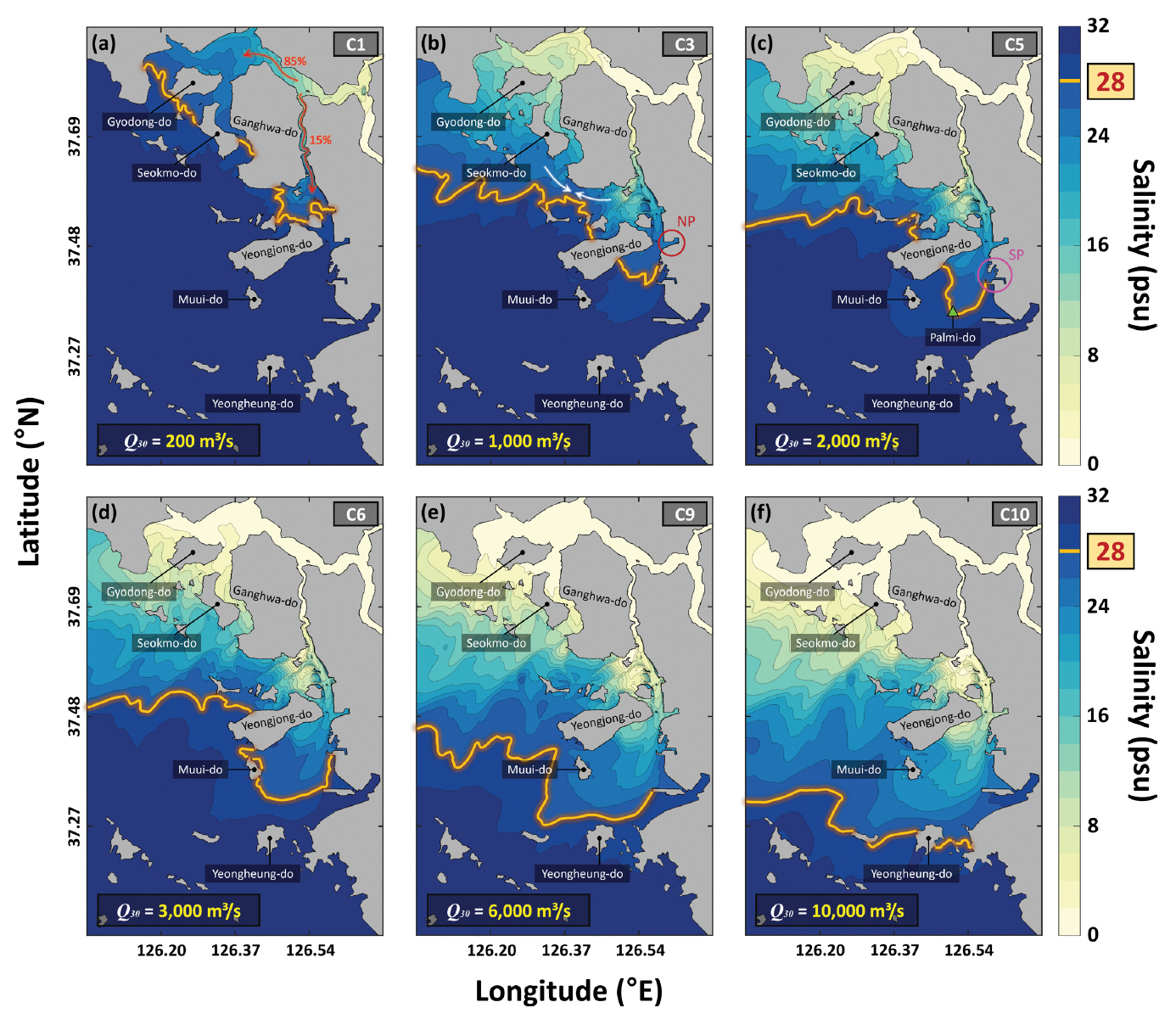
Figure 5.Analysis of relationship between Q30 and D28: (a) distance of freshwater influence (DOFI) in A-B line for C1-C10, (b) region of freshwater influence (ROFI) in Gyeonggi Bay for C1-C10, and (c) simple non-linear regression analysis for Q30 and D28. The error bar in (c) means the maximum-minimum range of D28 during days 24~30 (see the yellow area in Figs. 3a and b). 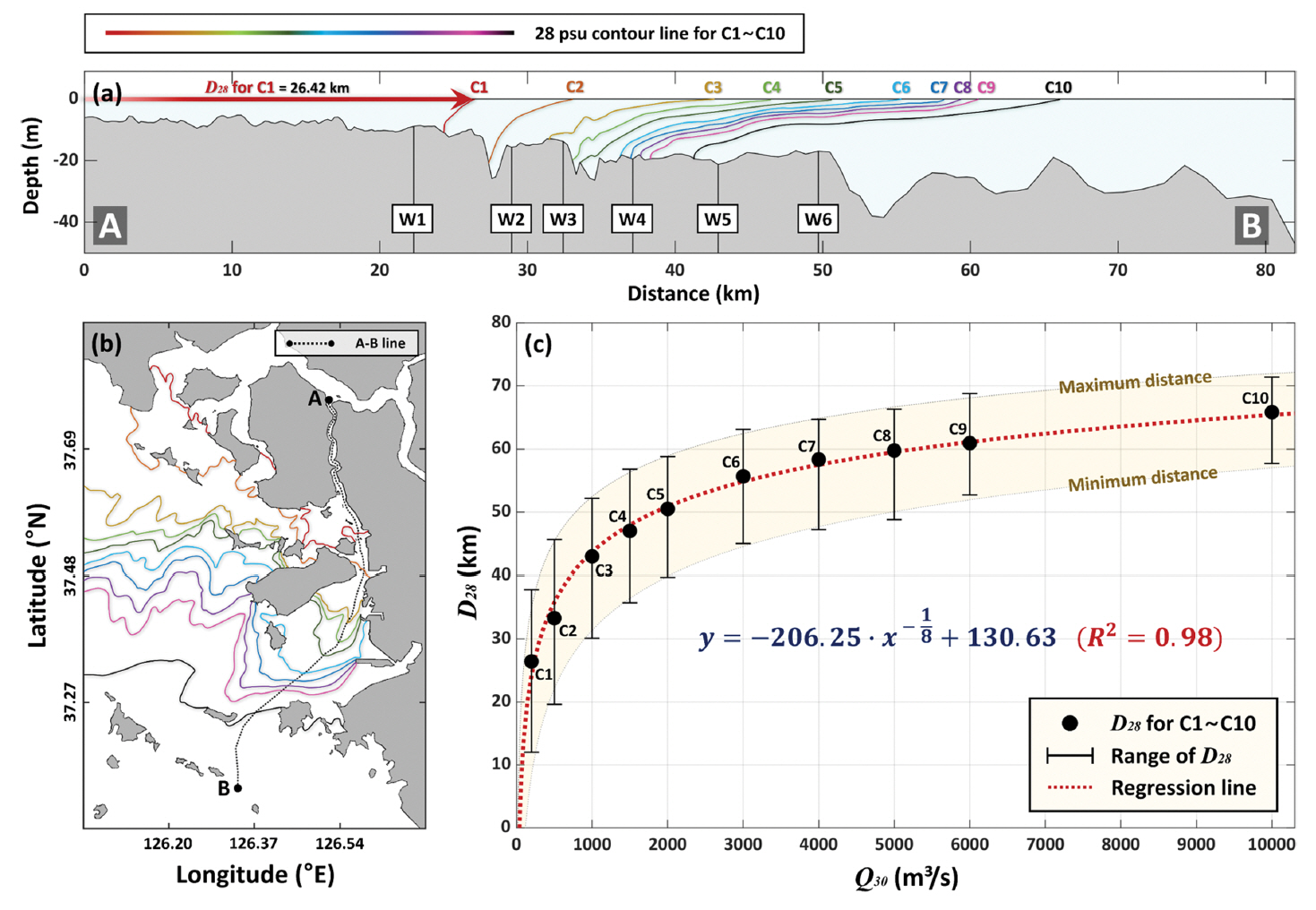
Table 1.Statistics for 11 wet seasons R1-R11 suggested by Fig. 2a
Table 2.10 numerical model scenarios for Q30
Table 3.List of Q30 corresponding to the observation dates of salinity measured at W1-W6 Table 4.
HA and HB for the regression equation of Q30 and Dn
ReferencesChen, C., Beardsley, R.C., Cowles, G., Qi, J., Lai, Z., Gao, G. and Ji, R. (2013). An unstructured grid, finite-volume community ocean model FVCOM user manual. SMAST (p. 404). UMASSD Technical Report-13-0701, University of Massachusetts-Dartmouth.
Chen, C., Liu, H., Beardsley, R.C. (2003). An unstructured grid, finite-volume, three-dimensional, primitive equations ocean model: application to coastal ocean and estuaries, Journal of Atmospheric and Oceanic Technology, 20(1):159-186.
Chen, C., Qi, J., Li, C., Beardsley, R.C., Lin, H., Walker, R., Gates, K. (2008). Complexity of the flooding/drying process in an estuarine tidal‐creek salt‐marsh system: An application of FVCOM, Journal of Geophysical Research: Oceans, 113(C7.
Cho, H.Y., Cho, B.J., Kim, S.J. (2008). Estimation on the regions of freshwater influence using the seasonal salinity data in Asan Bay coastal zone, Journal of Korean Society of Coastal and Ocean Engineers, 20(2):219-231 (in Korean).
Connor, D.W., Gilliland, P.M., Golding, N., Robinson, P., Todd, D. and Verling, E. (2006). UKSeaMap: The mapping of seabed and water column features of UK seas, Joint Nature Conservation Committee, Peterborough.
Flores, R.P., Rijnsburger, S., Horner‐Devine, A.R., Souza, A.J., Pietrzak, J.D. (2017). The impact of storms and stratification on sediment transport in the Rhine region of freshwater influence, Journal of Geophysical Research: Oceans, 122(5):4456-4477.
Horner-Devine, A.R., Hetland, R.D., MacDonald, D.G. (2015). Mixing and transport in coastal river plumes, Annual Review of Fluid Mechanics, 47, 569-594.
Jeong, H.H., Kang, S.D., Jung, H.J., Jeong, D.J., Oh, J.H., Choi, S.M., An, Y.K., Choo, H.S., Choi, S.D., Kim, S.S., Kim, P.J., Lee, W.C., Cho, H.S. (2017). The Current status of eutrophication and suggestions of the purification & restoration on surface sediment in the northwestern Gamak bay, Korea, 2017, Journal of the Korean Society for Marine Environment and Energy, 22(2):105-113 (in Korean).
Jeong, J.H., Kim, K.J., Yang, K.H., Chang, Y.Y., Park, S.H., Kim, Y.T. (2007). Study on the temporal and spatial variations of salinity by freshwater discharge in Gyeonggi Bay, Journal of Environmental Impact Assessment, 16(6):421-432 (in Korean).
Kim, D.Y., Yoon, C.G., Rhee, H.P., Choi, J.H., Hwang, H.S. (2019). Estimation of pollution contribution TMDL unit watershed in Han-River according to hydrological characteristic using flow duration curve, Journal of Korean Society on Water Environment, 35(6):497-509 (in Korean).
Kim, Y.T., Park, M., Kwon, H.H. (2020). Spatio-temporal summer rainfall pattern in 2020 from a rainfall frequency perspective, Journal of Korean Society of Disaster and Security, 93-104 (in Korean).
Lee, H.M., Kim, J.W., Choi, J.Y., Yoon, B.I., Woo, S.B. (2021). Mechanisms of salt transport in the Han River Estuary, Gyeonggi Bay, Journal of Korean Society of Coastal and Ocean Engineers, 33(1):13-29 (in Korean).
Lim, D.I., Rho, K.C., Jang, P.G., Kang, S.M., Jung, H.S., Jung, R.H., Lee, W.C. (2007). Temporal-spatial variations of water quality in Gyeonggi Bay, west coast of Korea, and their controlling factor, Ocean and Polar Research, 29(2):135-153 (in Korean).
Park, G.S. (2004). Salinity distribution and ecological environment of Han river estuary, Journal of Wetlands Research, 6(1):149-166 (in Korean).
Park, H.J., Min, B.H. (2018). Stress responses of Olive Flounder (Paralichthys olivaceus) to salinity changes, Korean Journal of Ichthyology, 30(1):1-8 (in Korean).
Park, K., Oh, J.H., Kim, H.S., Im, H.H. (2002). Case study:mass transport mechanism in Kyunggi Bay around Han River mouth, Korea, Journal of Hydraulic Engineering, 128(3):257-267.
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||