1. 서 론
평균월파량은 항만 및 해안구조물의 마루높이를 설정하는 데 있어 필요한 중요한 설계요소로서 오랜 기간동안에 걸쳐 유럽을 중심으로 많은 연구자들에 의해 다양한 경험식들이 제안되었다(Owen, 1982; Bradbury and Allsop, 1988; van der Meer and Janssen, 1995; Pedersen, 1996; van der Meer and Bruce, 2014; Altomare et al., 2016). 직립식 및 경사식 구조물을 대상으로 평균월파량 산정과 관련된 대표적인 연구성과로는 EurOtop(2018)을 들 수 있다. 그러나 유럽을 중심으로 제안된 경험식들을 국내 설계시 적용하는데 있어 유의할 사항들이 있다. 기 제안된 많은 경험식들이 비쇄파조건을 대상으로 한 것이 많으며, 적용된 피복재 또한 다르다. 유럽에서는 주 피복재로 사석을 적용하는 경우가 많은 반면, 국내에서는 주 피복재로 콘크리트블록을 주로 사용하는 차이가 있다. 또한 국내에서는 중간 피복층에 콘크리트블록을 적용하는 경우가 많으며, 중간피복층에 사석을 적용하는 것과 투수성의 차이가 발생된다. 따라서 국내외의 기존 연구성과를 활용하는 경우에 파랑조건뿐만 아니라 단면의 기하학적 제원 등이 설계조건에 부합되는지 확인하는 과정이 필수적이다. 예를 들어, 국내에서 가장 많이 적용되고 있는 테트라포드가 피복된 경사식 구조물의 경우에 EurOtop(2018)의 제안식은 테트라포드가 전사면 피복된 조건에 대한 식으로서 과소하게 월파량을 추정하는 것으로 알려져 있다(Yoo et al., 2024).
국내에서는 항만 및 해안구조물 설계시 항만 및 어항 설계 기준(MOF, 2020)을 활용하고 있으며, 평균월파량 산정과 관련된 사항은 일본의 연구결과가 수록되어 있으나 국내 연구 성과를 활용하는 방안으로 개정하는 작업중에 있다. 최근 들어 직립식 및 경사식 구조물의 평균월파량 산정과 관련된 여러 국내연구가 진행되고 있으며, 지속적인 연구성과가 제시되고 있다(Kim and Lee, 2012, 2023; Lee and Kim, 2023; Yoo et al., 2024). Kim and Lee(2012, 2023)는 직립식 구조물의 평균월파량 산정 경험식을 제안하였으며, Yoo et al.(2024)는 경사식 구조물의 상대여유고가 낮은 조건에 대해 실험을 실시하고, 결과를 제시하였다. Lee and Kim(2023)은 테트라포드가 피복된 경사식 구조물을 대상으로 평균월파량을 산정할 수 있는 경험식의 기본형을 제안하였다.
본 연구에서는 경사식 구조물을 대상으로 평균월파량 산정을 위한 수리모형실험을 수행하였으며, Lee and Kim(2023)이 고려하지 않은 사항을 검토하는 것이다. 주된 실험의 목적은 제체 사면경사의 변화 및 피복재 어깨폭의 변화가 월파량에 미치는 영향을 검토하는 것이다. 수리모형실험은 2차원 수로에서 여러 수심조건, 다양한 파랑조건 및 상대여유고 조건 등에 대해 수행되었으며, 불규칙파를 적용하였다. 수행된 실험결과는 Lee and Kim(2023)이 제안한 경험식에 제체 사면경사 및 피복재 어깨폭의 영향을 포함하여 평균월파량을 산정할 수 있는 경험식을 제안하였다.
2. 실험시설 및 실험조건
2.1 실험시설
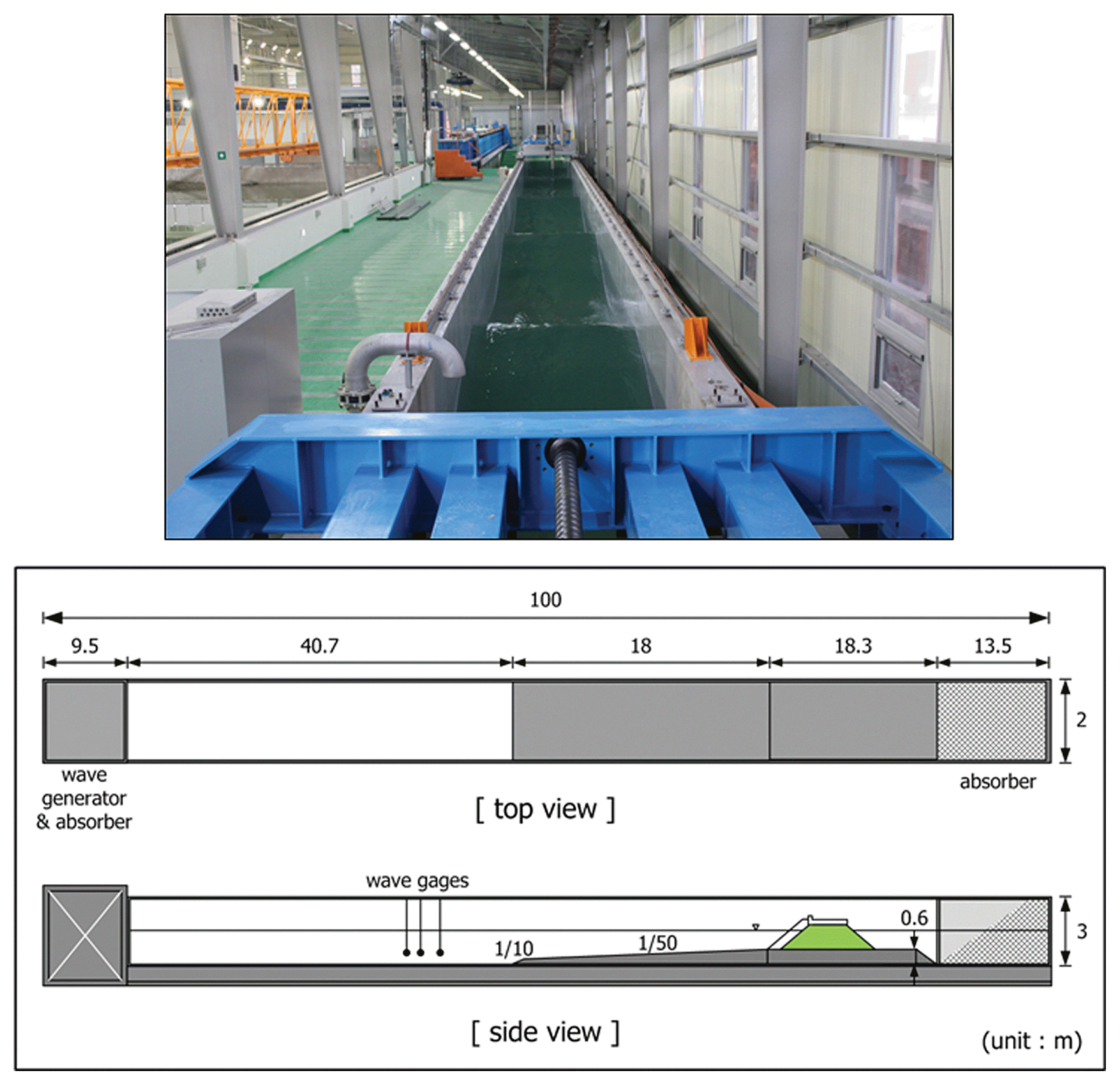
본 실험은 전남대학교 해안항만실험센터 2차원 수로에서 수행되었으며, 사용된 수로의 제원은 폭 2 m, 길이 100 m, 높이 3 m이며, 전기서보피스톤식 조파기가 설치되어 있고, 규칙파 및 불규칙파를 조파할 수 있다. 또한 조파판 전면에 부착된 파고계를 이용하여 독취한 자료를 바탕으로 반사파 흡수식 제어가 가능하고 수로 양쪽 끝부분에는 소파시설이 설치되어 있다. 설치된 조파기의 성능은 최대파고 1.3 m, 재현 가능 주기 0.5~10 sec이다. 본 실험에서 실험파 설정 및 실험시 입사파의 증폭 유무를 확인하기 위해 구조물 전면에 설치한 파고계는 용량식으로서 계측범위는 ± 75 cm이다. 월파량은 월파량 수집장치에 수중펌프 및 유량계를 설치하여 연속적으로 계측하였다. Fig. 1은 단면수로의 개념도이다.
2.2 실험조건
본 실험에 적용된 목표 실험파는 Table 1에 제시되어 있다. 목표 실험파의 유의파주기(significant wave period, TS) 및 유의파고(significant wave height, HS)는 각각 (TS)target = 2.1~3.6 sec, (HS)target = 0.16~0.36 m 범위이며, 유의파주기는 (∆TS)target = 0 .3 sec 간격, 유의파고는 (∆HS)target = 0.04m 간격으로 설정하였다. 그리고 구조물이 설치되는 수심(d)은 d = 0.4, 0.55, 0.7 m로서 실험에 적용된 실험파는 쇄파 및 비쇄파가 포함된 수심조건이다. Table 1에 제시된 파랑제원은 목표 파랑제원이며, 실험결과 분석시에는 실험파 설정시 구조물 설치위치에서 계측된 자유수면으로부터 분석된 각 수심별 파랑제원(유의파주기 TS 및 유의파고 HS)을 이용하였다. 즉, 실험파는 쇄파가 발생하지 않는 수심(조파기 전면 수심)에서 목표파랑 및 스펙트럼을 설정하고, 구조물 위치에서는 계측된 유의파고 및 유의주기를 분석하였다. 조파기 전면과 구조물 설치위치 사이에는 1/50의 일정한 경사면이 설치되어 있으며, 파랑이 사면을 따라 진행하면서 쇄파가 발생되도록 하였다(Fig. 1 참조). 조파기 전면에서 목표 파랑을 재현하였을 경우에 구조물 설치위치에서 d = 0.4 m인 경우에 HS = 0.156~0.208 m, d = 0.55 m인 경우에 HS = 0.168~0.288 m, d = 0.7 m인 경우에 HS = 0.212~0.324 m 범위의 유의파고가 설정되었다.
본 실험은 평균월파량을 산정하기 위한 실험으로서 조파시간은 목표 유의파주기 기준으로 600파이며, 월파량 계측은 각각의 유의파 주기 기준으로 100파 후 500파 시간동안을 대상으로 하였다. 즉, 평균월파량은 목표 유의파주기별 500파 시간동안 계측된 전체 월파량을 이용하여 분석하였다.
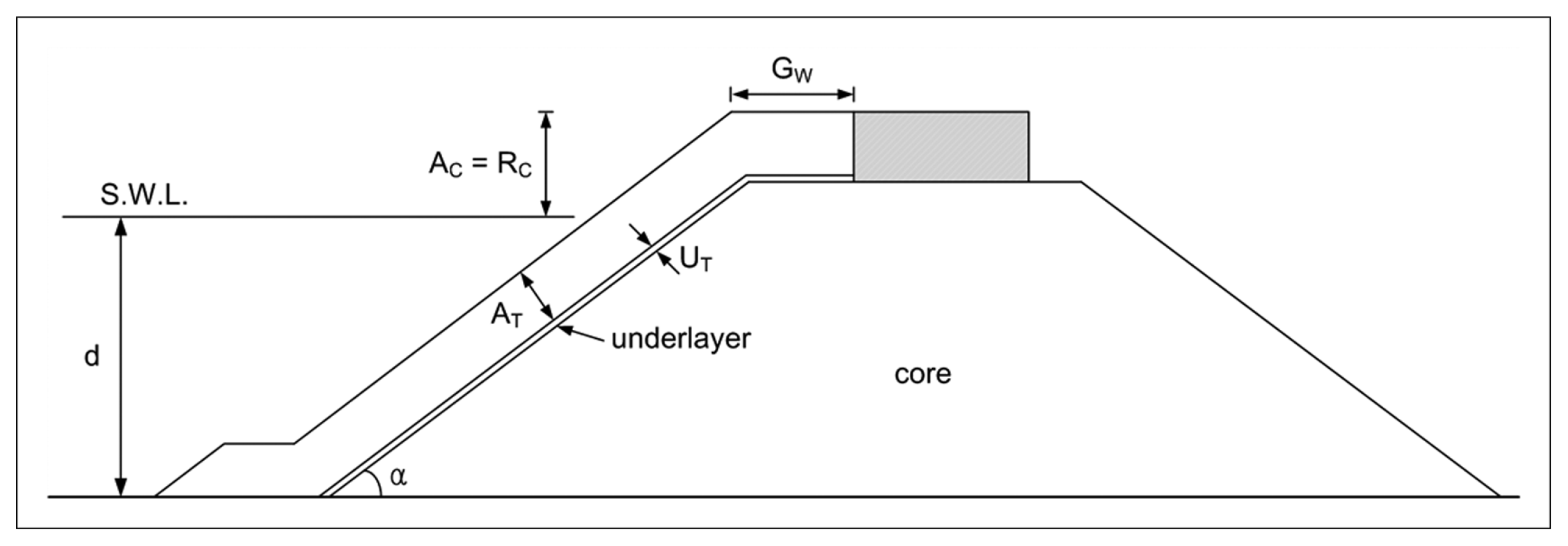
본 실험에 적용된 실험단면은 Fig. 2와 같은 경사식 구조물이다. Fig. 2에서 RC는 여유고(freeboard), AC는 피복재 높이(crest height of armor block), GW는 상치콘크리트 전면 피복재 어깨폭(width of armour crest), AT는 주 피복층 두께(armour layer thickness), UT는 중간 피복층 두께(underlayer thickness)이고, α는 제체 사면경사이다. 본 실험에서 적용한 모형구조물의 기하학적 제원은 Table 2와 같다. 실험에서 피복재 높이와 상치콘크리트 높이가 같은 조건(RC/AC = 1)을 대상으로 하였으며, 상대여유고(R = RC/HS)는 R = 0.77~2.22 범위이다. 주 피복재인 테트라포드는 2층 정적으로 피복하였으며, 피복두께(AT)는 서로 다른 피복재의 크기를 적용하여 0.2 m와 0.22 m이고, 트라이포드(tripod)가 설치된 중간 피복층의 두께(UT)는 0.035 m이다. 그리고 상치콘크리트 전면 피복재 어깨폭(GW)은 0.252 m(GW/Dn = 2.32), 0.352 m(GW/Dn = 3.79), 0.404 m(GW/Dn = 3.72), 0.556 m(GW/Dn = 5.12), 0.86 m(GW/Dn = 7.92)이다. 여기서, Dn(= V1/3)은 피복재의 공칭길이(nominal length)이고, V는 사용된 피복재의 체적이다. 또한 제체 사면경사도 월파량의 변화에 영향을 미치기 때문에 본 실험에서는 cotα = 1.5와 cotα = 2.0을 적용하였다.
3. 결과분석
Lee and Kim(2023)은 RC = AC, GW/Dn = 3 .79, cotα = 1.5인 조건에 대해 수리모형실험을 수행하고, 기존 연구성과와의 비교 및 적정 무차원변수에 대한 검토 후에 경사식 구조물의 평균월파량을 산정할 수 있는 경험식을 제안하였다. 본 논문에서는 이와 관련된 일반적인 사항은 생략하였고, Lee and Kim(2023)을 참조할 수 있다.
본 실험은 Lee and Kim(2023)이 수행한 연구의 후속 실험이며, 경사식 구조물의 제체 사면경사와 피복재 어깨폭이 평균월파량에 미치는 영향을 검토하기 위한 것으로 Lee and Kim(2023)의 실험결과도 포함하여 분석하였다.
3.1 제체 사면경사 영향
국내에서는 경사식 구조물 설계시 일반적으로 cotα = 1.5의 제체 사면경사를 적용하고 있으며, 피복재의 안정 확보 등의 사유로 cotα = 2.0의 제체 사면경사가 일부 적용되고 있는 실정이다.
본 연구에서는 제체 사면경사가 평균월파량에 미치는 영향을 검토하기 위해 RC = AC, GW/Dn = 3 .79, cotα = 2.0인 조건에 대해 실험을 수행하고, cotα = 1.5인 조건의 실험결 과와 비교하였다.
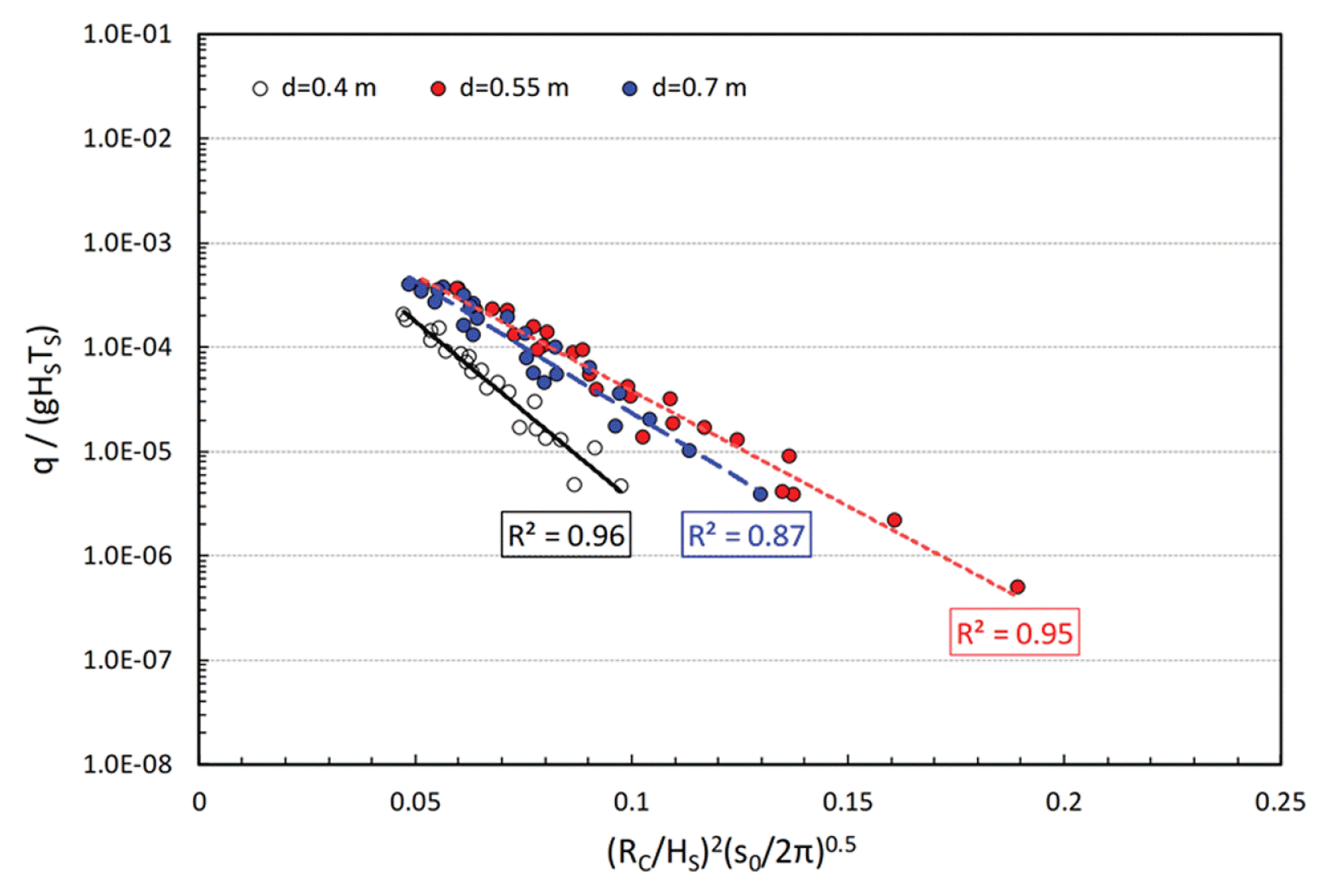
Fig. 3은 Bradbury and Allsop(1988)의 무차원변수를 이용하여 cotα = 2.0인 조건의 실험결과를 나타낸 것으로서 각 수심별 상관계수(R2)는 비교적 높게 나타났다. 수심이 d = 0.40 m인 조건에서 가장 적은 평균월파량이 계측되었으며, 이는 쇄파가 영향을 미치기 때문으로 판단된다. d = 0.55 m와 d = 0.70 m인 경우에는 d = 0.55 m인 경우가 약간 많은 월파가 계측되었으나 그 차이는 크지 않았다.
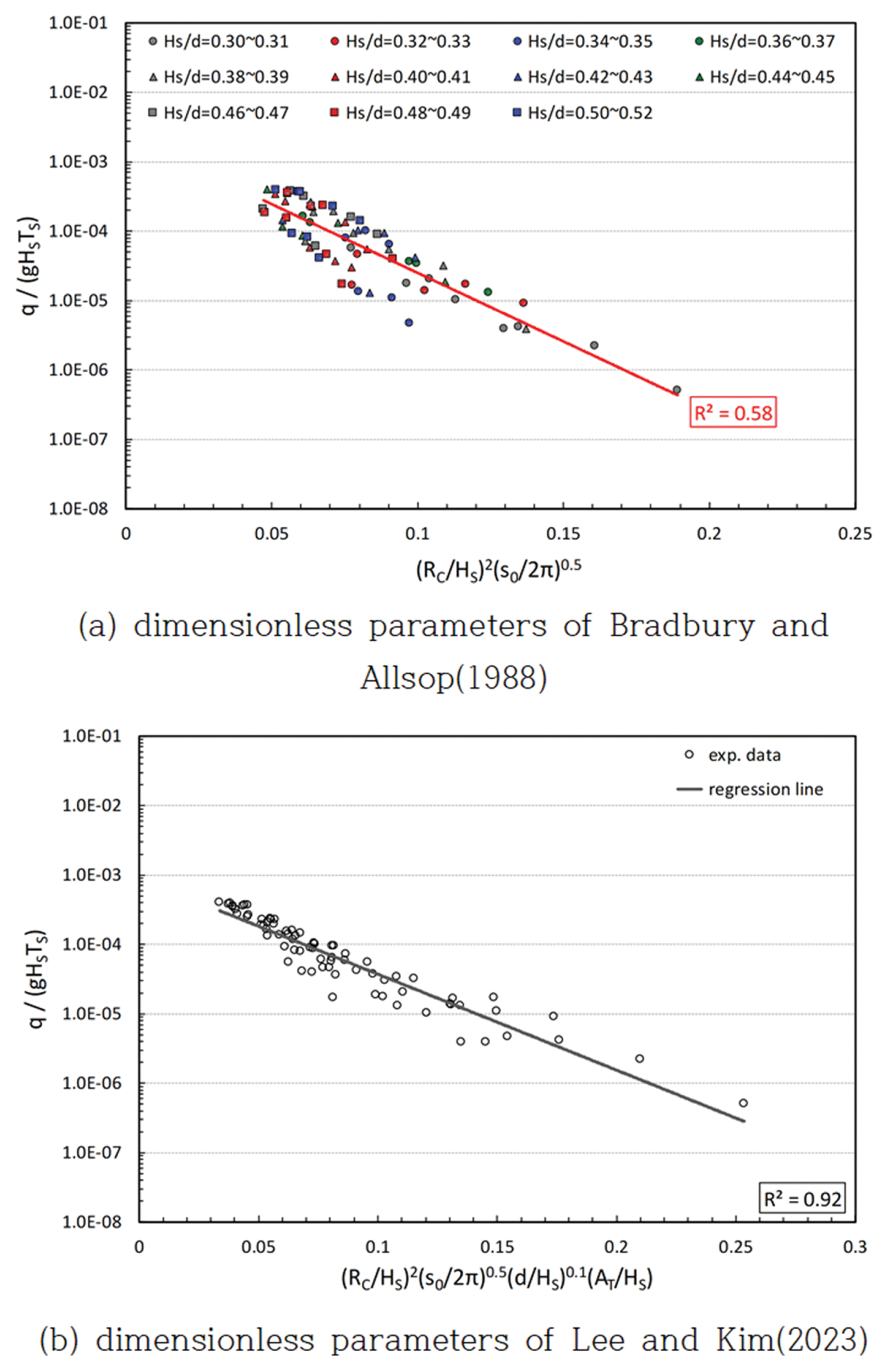
Fig. 4(a)는 Bradbury and Allsop(1988)의 무차원변수를 이용하여 cotα = 2.0인 조건의 실험결과를 수심조건과 관계없이 전체 결과를 상대파고(HS/d)별로 도시한 것으로 계측자료의 분산이 크게 발생하였으며, 상관계수는 R2 = 0.58로 낮게 나타났다. 즉, 상대여유고(RC/HS)와 파형경사(s0 = HS/L0) 만으로는 쇄파의 영향을 적절히 고려하지 못함을 의미한다. 여기서, L0는 유의파주기에 대응하는 심해파장이다. Fig. 4(b)는 Lee and Kim(2023)의 무차원변수를 이용하여 실험결과를 도시한 것으로서 Fig. 4(a)보다 상관계수가 상대적으로 높게 나타남을 알 수 있다. 즉, 구조물 전면에서의 유의파고와 수심의 비인 상대파고(HS/d)를 추가로 고려함으로서 쇄파의 영향을 어느 정도 고려할 수 있기 때문으로 판단된다.
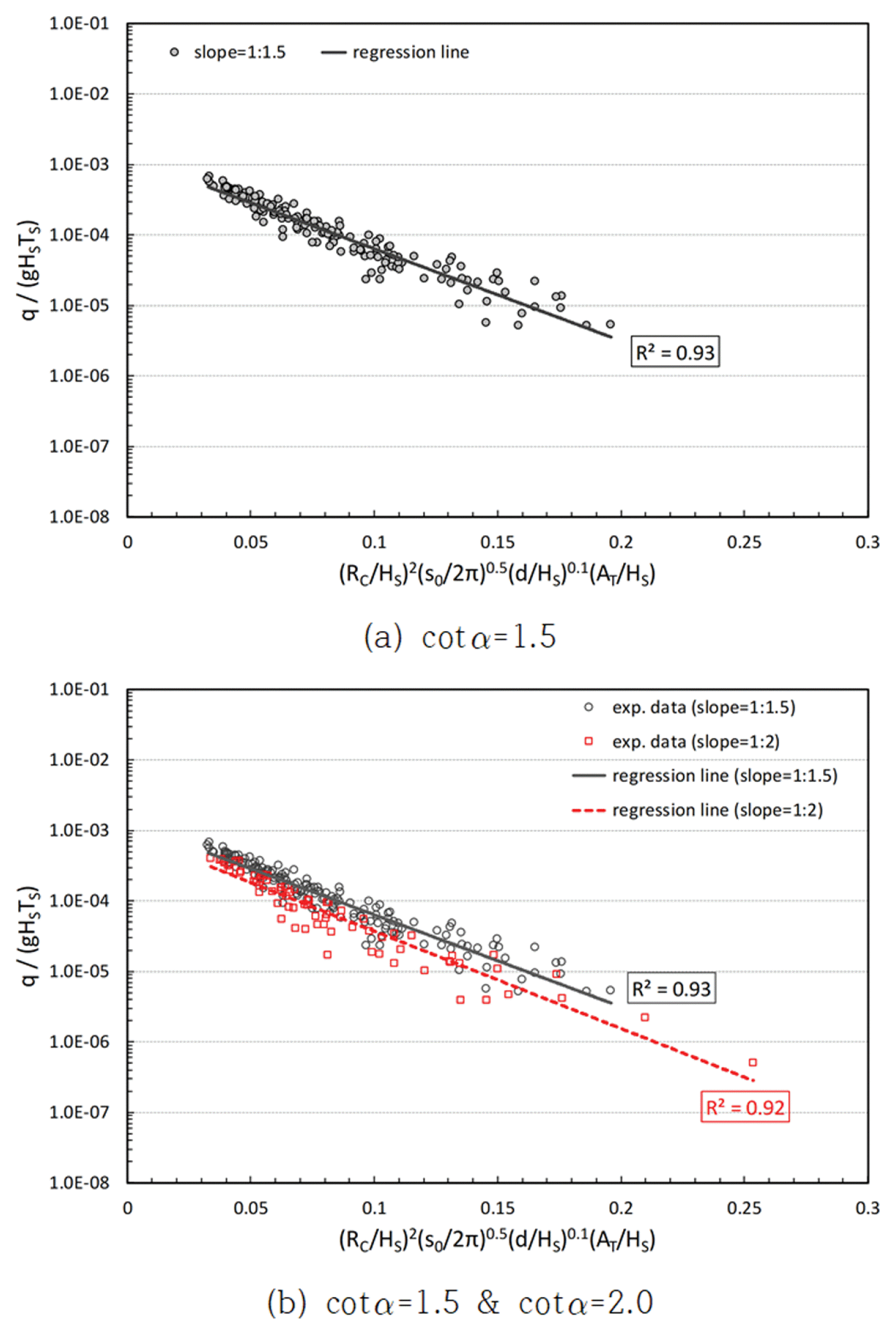
Fig. 5는 제체 사면경사 cotα = 1.5와 cotα = 2.0의 결과를 상대여유고(RC/HS), 파형경사(s0 = HS/L0), 상대파고(HS/d) 및 상대 피복층 두께(AT/HS)의 무차원변수를 이용하여 도시한 것이다. Fig. 5(a)는 cotα = 1.5 조건에 대한 Lee and Kim(2023)의 결과로서 상관계수는 R2 = 0.93이다. Fig. 5(b)는 cotα = 2.0 조건에 대한 결과인 Fig. 4(b)와 Fig. 5(a)의 cotα = 1.5를 비교한 것으로서 cotα = 2.0 조건이 cotα = 1.5 조건에 비해 평균월파량이 다소 적게 나타남을 알 수 있으며, 전체적인 기울기는 유사하게 나타났다.
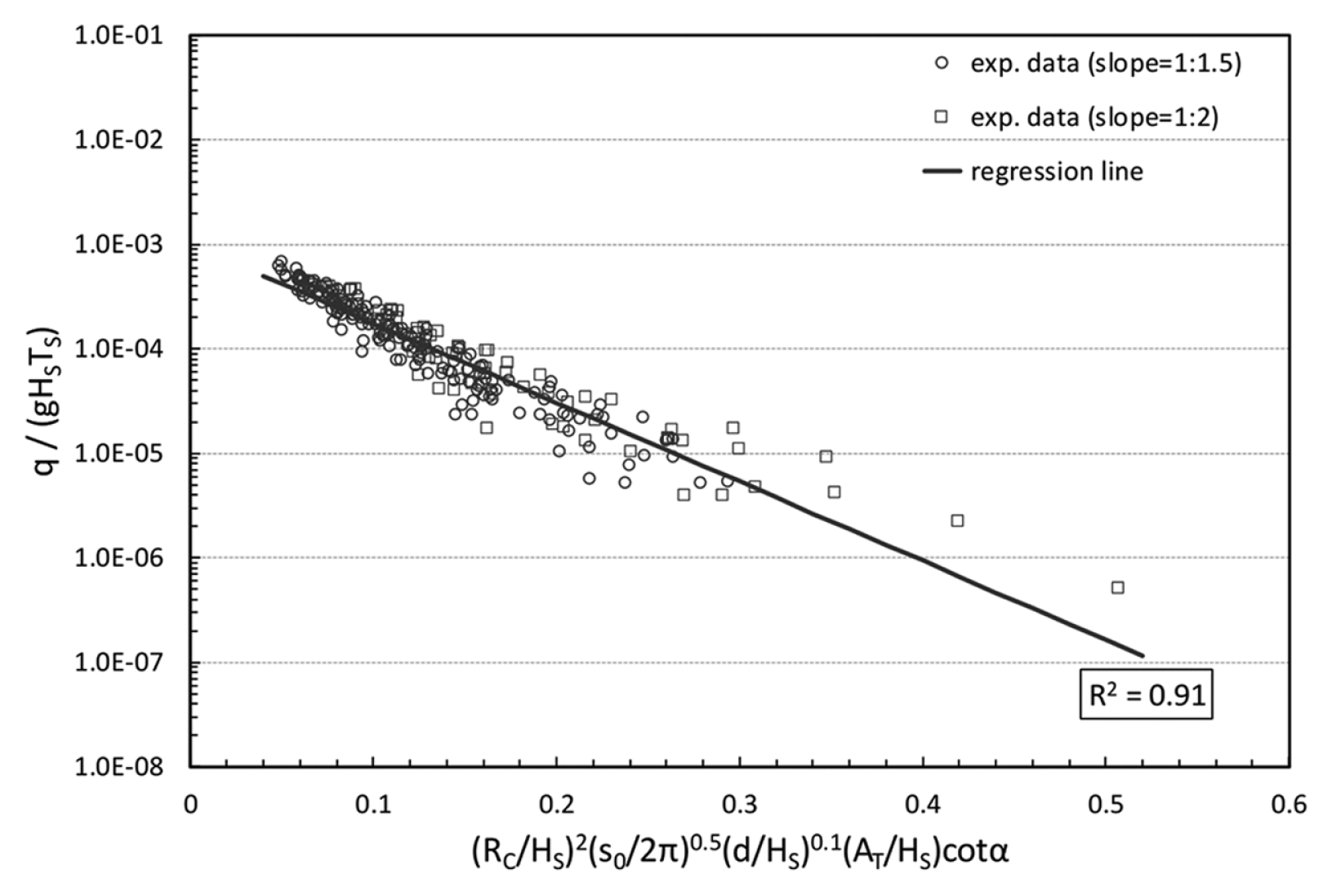
Fig. 6은 횡축의 무차원변수에 제체 사면경사 cotα를 포함하여 cotα = 1.5와 cotα = 2.0의 결과를 같이 도시한 것으로서 상관계수는 R2 = 0.91로 나타났다. 즉, cotα = 1.5와 cotα = 2.0인 경우에는 무차원변수로 cotα를 고려하면 제체 사면경사에 따른 월파량의 변화를 적절히 고려할 수 있음을 의미한다.
3.2 피복재 어깨폭의 영향
피복재 어깨폭이 월파량의 변화에 미치는 영향은 Table 2에서 피복재 어깨폭 GW = 0.252 m(GW/Dn = 2.32), 0.404 m(GW/Dn = 3.72), 0.556 m(GW/Dn = 5.12), 0.86 m(GW/Dn = 7.92)를 대상으로 수심 d = 0.55 m, 0.70 m 조건에서 cotα = 1.5 및 AT = 0.22 m를 적용하여 월파량 계측실험을 수행하고, 결과를 검토하였다.
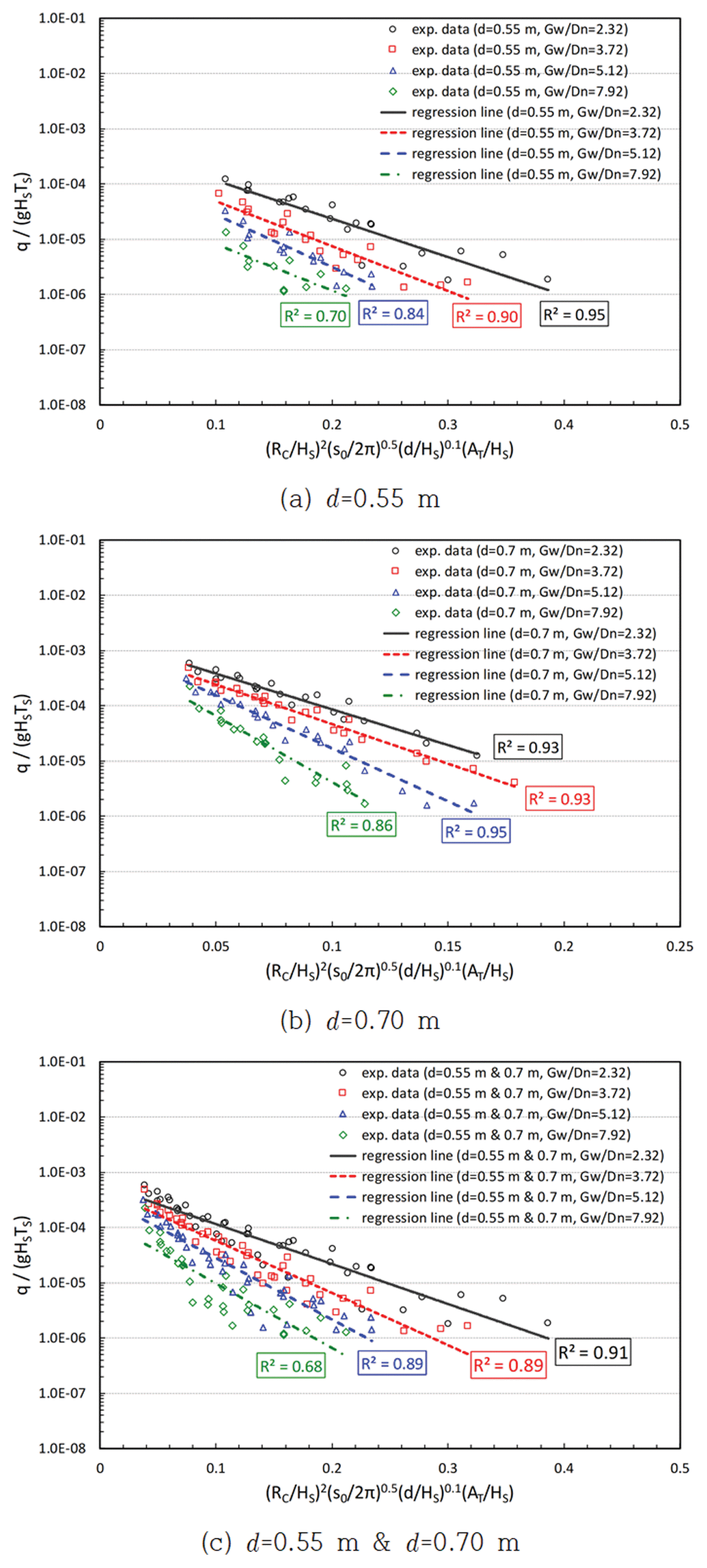
Fig. 7(a, b)는 각각 d = 0.55 m와 d = 0.70 m의 결과를 상대여유고(RC/HS), 파형경사(s0 = HS/L0), 상대파고(HS/d) 및 상대 피복층 두께(AT/HS)의 무차원변수를 이용하여 도시한 것이다. 전체적으로 피복재 어깨폭이 증가할수록 평균월파량은 감소하는 것으로 나타났다. Fig. 7(c)는 d = 0.55 m와 d = 0.70 m의 결과를 통합하여 도시한 것으로서 전체적인 경향은 각 수심별 경향과 유사하게 나타났다. GW/Dn = 7.92의 경우에는 피복재 어깨폭이 상당히 넓어 계측된 월파량이 적기 때문에 실험결과의 분산이 다소 크게 나타나 상관계수가 낮게 나타났다. 그러나 GW/Dn = 7.92 이외의 다른 조건에서는 상관계수는 비교적 높게 나타났다.
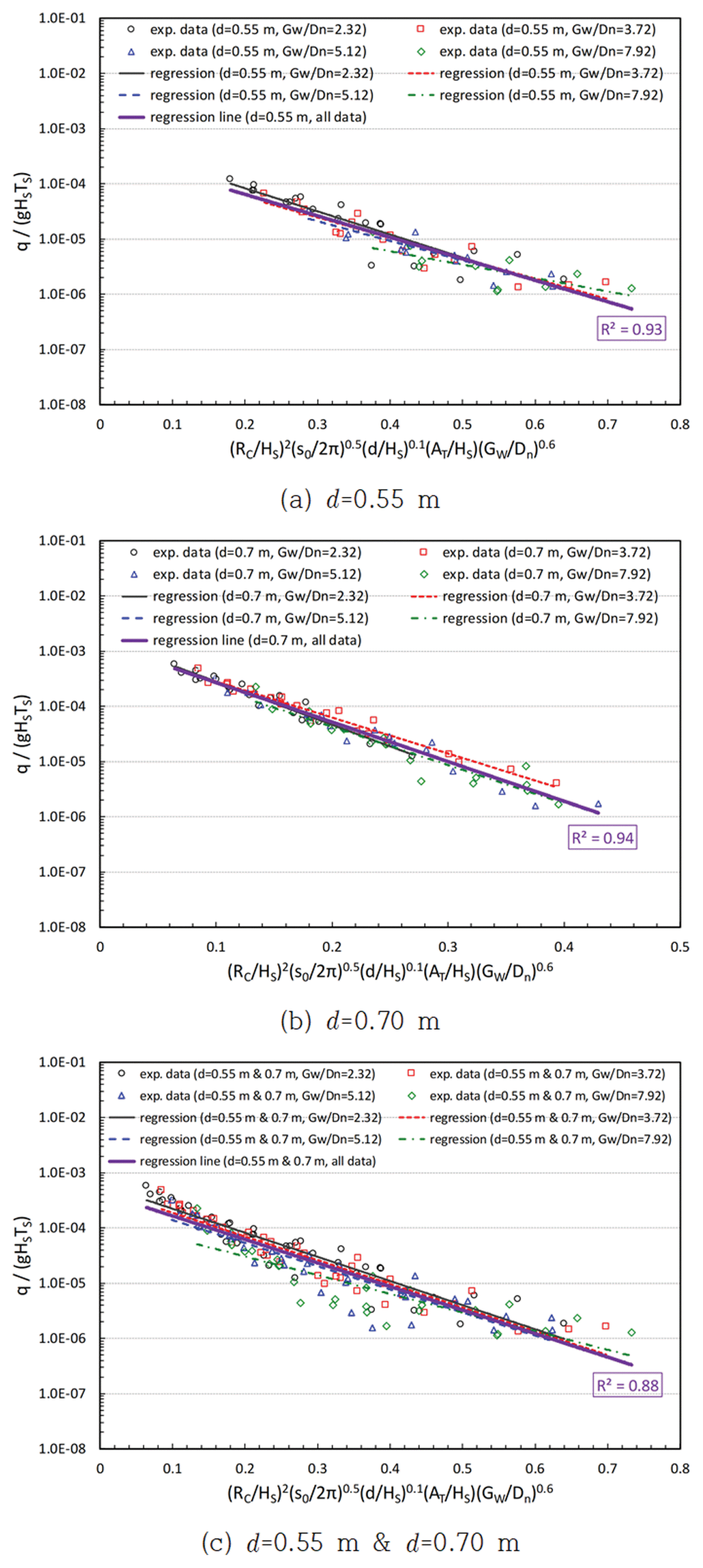
Fig. 8은 피복재 어깨폭의 영향을 고려하기 위해 무차원변수로 상대 피복재 어깨폭(GW/Dn)을 고려하여 결과를 도시한 것으로 전체적으로 피복재 어깨폭의 영향이 잘 고려되고 있으며, 전체 실험결과가 하나의 경향으로 비교적 잘 수렴됨을 알 수 있다.
3.3 경사식구조물의 평균월파량 산정 경험식
마루높이(RC)와 피복재 높이(AC)가 동일한 경사식 구조물평균월파량 산정을 위한 경험식을 도출하기 위해 Lee and Kim(2023)의 cotα = 1.5 결과와 본 실험에서 수행한 제체사면경사 cotα = 2.0 및 피복재 어깨폭에 결과를 포함하여 분석하였다.
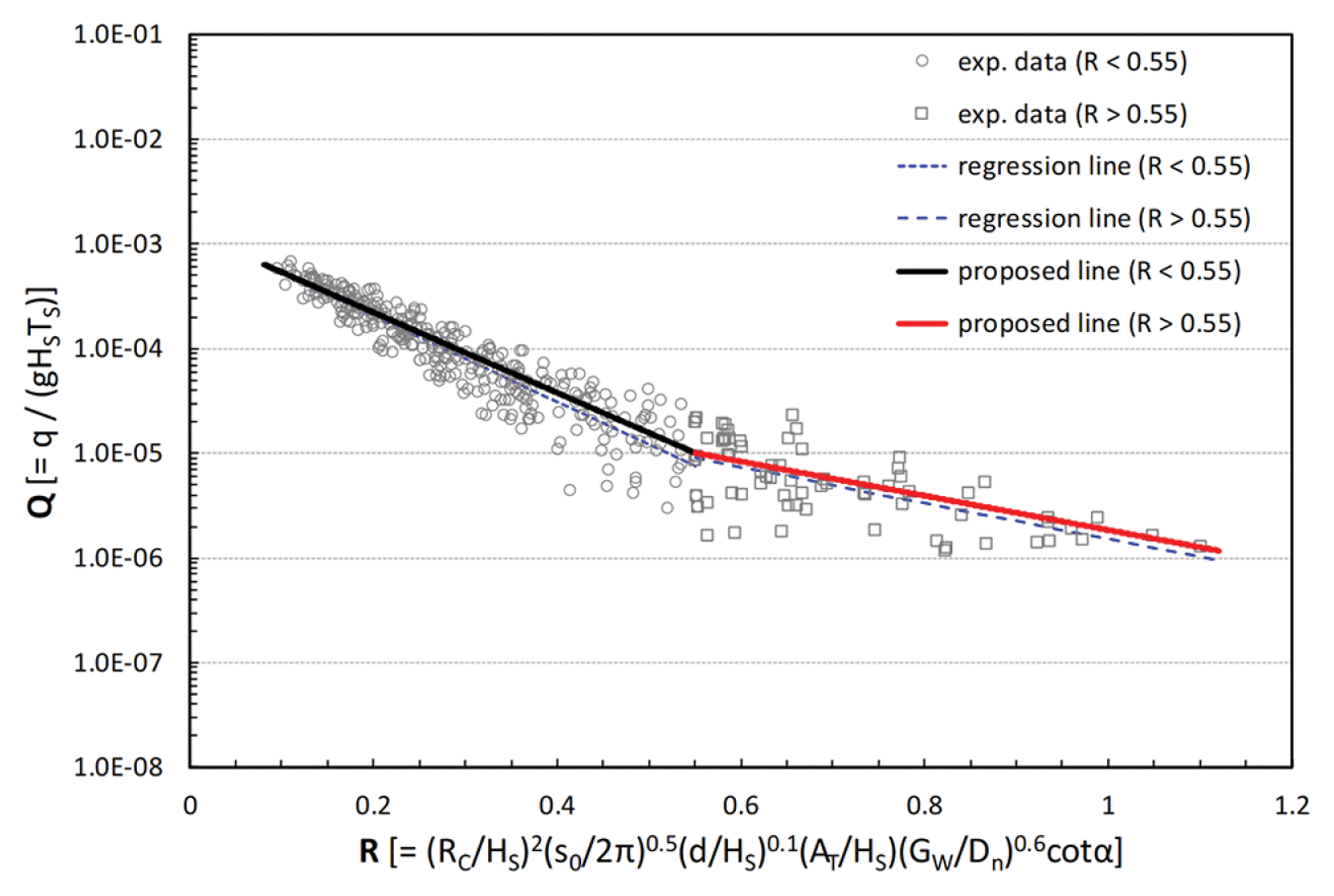
Fig. 9는 Lee and Kim(2023)의 무차원변수에 상대 피복재 어깨폭[(GW/Dn)γ]과 제체 사면경사 cotα를 추가하여 무차원 월파량을 도시한 것이다. 실험결과 분석시 상대 피복재 어깨폭의 가중치(γ)는 γ = 0.6이 가장 적절한 것으로 검토되었다. 본 연구에서 제안하는 경험식은 지수형으로서 식(1)과 같으며, a와 b는 경험식의 계수이다.
식(1)에서 Q는 무차원 평균월파량이고, R은 무차원 변수로서 식(2)와 같다. 식(2)에서 q는 단위폭당 단위시간당 평균월파량, g는 중력가속도이다.
본 연구에서는 Fig. 9에서 알 수 있는 바와 같이 R = 0.55를 기준으로 경험식의 계수 a와 b를 각각 다르게 제안하였다. 실험결과 분석시 하나의 경험식 계수로도 검토하였지만 적절하지 않은 것으로 판단하였다.
본 실험결과를 이용하여 R = 0.55으로 구분하여 분석된 경험식의 계수 a와 b는 식(3)과 같다. 그러나 식(3)을 적용할 경우에는 R = 0.55에서 불연속이 발생한다(Fig. 9 참조).
Fig. 9에서 볼 수 있는 바와 같이 실험결과는 일정수준의 분산이 존재한다. 본 연구에서는 약간 보수적인 평균월파량 산정을 위해 0.05σ를 할증하고, R = 0.55에서 불연속이 발생하지 않도록 조정하여 식(4)와 같은 경험식의 계수 a와 b를 제안하고자 한다. 여기서, σ는 무차원 월파량의 표준편차이다.
식(1)~(4)의 적용범위는 RC/HS = 0.77~2.0, s0 = 0.007~0.049, HS/d = 0.30~0.53, AT/HS = 0.60~1.52, GW/Dn = 2.32~7.92, cotα = 1.5 및 2.0이다. 식(1)~(4)의 적용범위 내에서 평균월파량 산정식을 적용하는 것이 바람직하지만, Fig. 9의 경향으로 미루어 일부 적용범위를 벗어난 경우에도 적용이 가능할 것으로 판단된다.
4. 결 론
본 연구에서는 마루높이와 피복재의 피복높이가 동일한 조건에서 테트라포드가 2층 피복되고, 중간피복층으로 트라이포드가 설치된 경사식 구조물을 대상으로 제체 사면경사와 피복재 상단 어깨폭의 변화가 평균월파량에 미치는 영향을 2차원 실험을 통해 검토하였다.
주요 실험결과를 요약하면 다음과 같다.
(1) 제체 사면경사 cotα = 2.0인 경우가 cotα = 1.5인 경우에 비해 월파량이 감소하였다.
(2) 피복재 상단 어깨폭이 증가할수록 월파량은 감소하였다. 즉, 동일 상대여유고 조건에서 피복재 어깨폭을 증가시킴으로서 월파량을 저감시킬 수 있다.
(3) 경사식 구조물의 상치콘크리트 마루높이와 피복재 높이가 같은 조건에 대해 평균월파량을 산정할 수 있는 경험식을 제안하였다. 무차원변수로 상대여유고, 파형경사, 상대파고, 상대 피복층 두께, 상대 피복재 어깨폭을 적용하였고, 제체 사면경사는 cotα = 1.5 및 cotα = 2.0에 적용 가능하다.
본 연구에서 제안하는 경사식 구조물의 평균월파량 산정을 위한 경험식은 다음과 같다.
여기서, Q는 무차원 평균월파량이고, R은 무차원변수이다.
본 연구에서는 상치콘크리트의 마루높이와 피복재높이가 동일한 조건(RC/AC = 1)을 대상으로 하였으나, 항만 및 호안구조물 설계시에는 파라펫이 설치되는 경우(RC/AC > 1)가 다수 있다. 따라서, 평균월파량 산정식에 RC/AC > 1인 조건이 포함되도록 개선할 필요가 있다. 이와 관련하여 수리모형실험이 진행중에 있으며, 추후 결과를 제시하고자 한다.