기상청 지진 자료를 이용한 내진설계 지진규모의 신뢰구간 추정

Technical Notes

J Korean Soc Coast Ocean Eng 2017; 29(1): 62-66.

Published online: February 28, 2017

DOI: https://doi.org/10.9765/KSCOE.2017.29.1.62

기상청 지진 자료를 이용한 내진설계 지진규모의 신뢰구간 추정

조홍연*, 이기섭**

*한국해양과학기술원 해양자료과학연구실

**부산대학교 해양학과

Confidence Interval Estimation of the Earthquake Magnitude for Seismic Design using the KMA Earthquake Data

Hong Yeon Cho*, Gi-Seop Lee**

*Ocean Data Science Lab., Korea Institute of Ocean Science and Technology, 787 Haeanro, Ansan, Gyeonggi, 15627, Korea

**Dept. of Oceanography, Pusan National Univ.

Corresponding author: Hong Yeon Cho, Ocean Data Science Lab., Korea Institute of Ocean Science and Technology, 787 Haeanro, Ansan, Gyeonggi, 15627, Korea, Tel:+82-31-400-6318, Fax:+82-31-400-7868, hycho@kiost.ac.kr

Received November 21, 2016       Revised December 22, 2016       Accepted January 10, 2017

Copyright: © Korean Society of Coastal and Ocean Engineers

This is an Open Access article distributed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted noncommercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Cited By
Citations to this article as recorded by
Probabilistic blast load for performance-based blast resistant design of building structures in petrochemical facilities
Seung-Hoon Lee, Bo-Young Choi, Han-Soo Kim
Journal of Building Engineering.2024; 98: 111313.     CrossRef
Case Study on Slope Stability Changes Caused by Earthquakes—Focusing on Gyeongju 5.8 ML EQ
Sangki Park, Wooseok Kim, Jonghyun Lee, Yong Baek
Sustainability.2018; 10(10): 3441.     CrossRef
Development of Design Blast Load Model according to Probabilistic Explosion Risk in Industrial Facilities
Seung-Hoon Lee, Bo-Young Choi, Han-Soo Kim
Journal of the Computational Structural Engineerin.2024; 37(1): 1.     CrossRef

요약

최근 발생한 기록적인 5.8 규모의 경주지진으로 한반도에서 발생 가능한 지진규모에 대한 관심과 해안구조물에 대한 내진 설계검토에 대한 요구가 고조되고 있다. 본 연구에서는 기상청에서 제공하는 지진규모 자료(규모 3.5, 4.0 이상의 자료)를 이용하여 비모수적인 극치해석 기법을 이용하여 재현기간에 따른 지진규모와 신뢰구간을 추정하였다. 지진규모 4.0 이상의 자료를 이용하여 추정한 결과, 재현기간 50, 100년에 해당하는 지진규모는 각각 5.81, 5.94, 추정 지진규모의 90% 신뢰구간은 각각 5.52-6.11, 5.62-6.29 범위로 추정되었다. 본 연구에서 추정한 지진규모는 공간적인 지진위험 영향을 반영하지 못하는 한계가 있으나, 한반도에서 발생 가능한 지진규모를 극치해석과 가용한 자료의 한정된 기간을 반영하여 신뢰구간을 추정하였기 때문에 다양한 연안 구조물의 설계 관점에서 활용이 가능하다.

핵심용어: 지진규모, 재현기간, 극치해석, 신뢰구간, Kernel 분포함수, 해안구조물

Abstract

The interest on the potential earthquake magnitude and the request on the earthquake-resistant design examination for coastal structures are emerged because of the recently occurred magnitude 5.8 earthquake in Gyeoung-Ju, Korea. In this study, the magnitude and its confidence intervals with the return periods are estimated using the KMA earthquake magnitude data (over 3.5 and 4.0 in magnitude) by the non-parametric extreme value analysis. In case of using the “over 4.0” data set, the estimated magnitudes on the 50- and 100-years return periods are 5.81 and 5.94, respectively. Their 90% confidence intervals are estimated to be 5.52-6.11, 5.62-6.29, respectively. Even though the estimated magnitudes have limitations not considering the spatial distribution, it can be used to check the stability of the diverse coastal structures in the perspective of the life design because the potential magnitude and its confidence intervals in Korea are estimated based on the available 38-years data by the extreme value analysis.

Keywords: Earthquake magnitude, return period, extreme value analysis, confidence intervals, Kernel distribution function, coastal structures

1. 서 론

한반도는 지진 안전지역이라는 기존의 인식이 있었지만, 2016년 9월 12일 경주에서 5.8 규모의 지진이 발생하고, 관측사상 최대 규모 기록을 갱신하면서 지진에 대한 우려가 확산되고 있다. 이러한 우려는 기존 항만 및 연안구조물의 내진설계에 대한 검토 요구로 이어지고 있다. 그러나 이러한 검토요구는 내진 설계방법에 대한 검토보다는 향후 발생 가능한 지진규모의 추정에 대한 검토가 선행되어야 한다. Kim et al.(2005)은 해안구조물의 내진성능 평가에 대한 연구를 수행한 바 있으며, Shin et al.(2013)은 동해 지진자료 발생빈도 해석에 혼합분포함수(mixed distribution function)를 적용한바가 있으나, 기상청에서 관측한 한반도에서 발생하는 지진자료를 이용하여 빈도해석을 실시한 연구는 제한되어 있는 상황이다.
본 연구에서는 한반도에서 발생한 가용한 지진규모 자료를 이용하여 극치분석을 수행하여, 장기 재현기간에 대한 지진규모와 지진규모의 신뢰구간을 추정하였다. 이 추정결과는 지진규모에 대한 막연한 우려보다는 관측 자료에 근거한 통계적인 추정에 근거를 두고 있으며, 지진규모와 내진설계에 이용되는 기초지반의 연직가속도로의 변환 과정을 포함하는 경우, 항만 및 어항 구조물 설계에 활용할 수 있다. 본 연구는 해안 구조물의 지진 안정 검토에 대한 기초 자료 제시를 목적으로 한다.

2. 재료 및 방법

2.1 KMA 지진자료

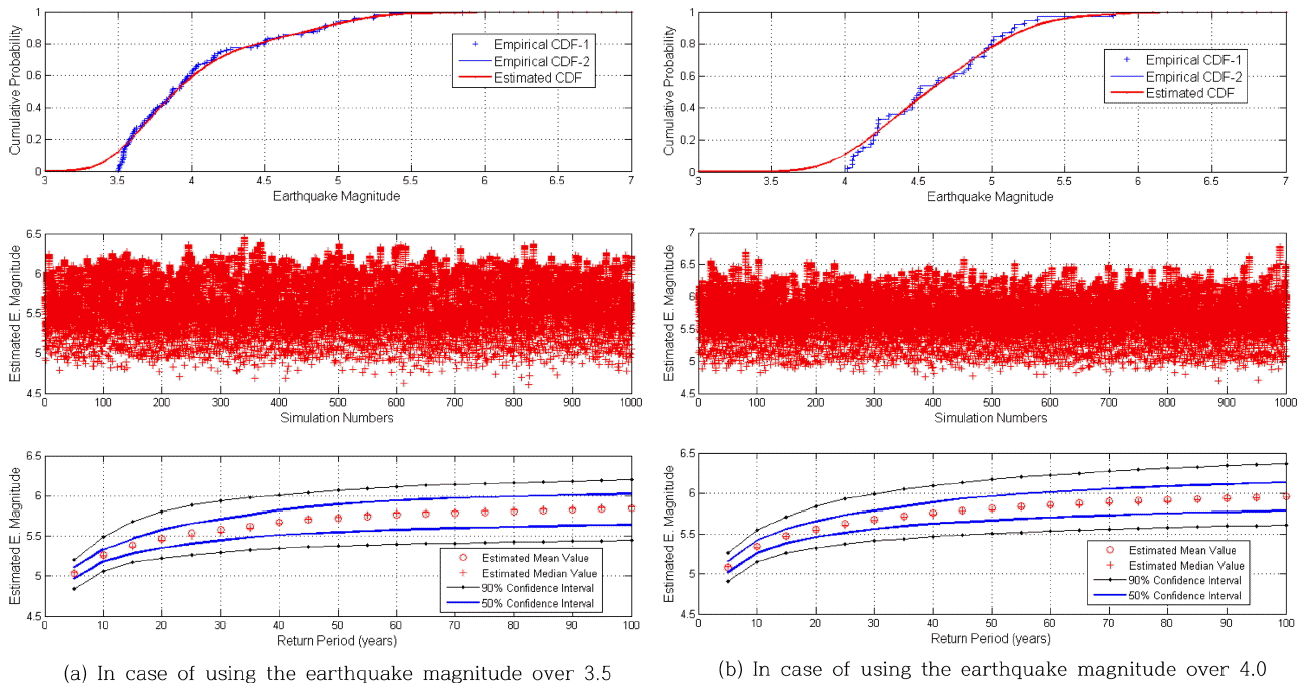
기상청에서는 1978년 8월 30일 관측 자료를 시작으로 현재(2016년 11월 10일)까지 지진규모 2.0 이상의 1,440개의 지진정보(발생일시 및 지점, 규모)를 제공하고 있다 (KMA, 2016; www.kma.go.kr → 날씨 → 지진·화산). 정보를 제공하는 기간은 총 38년 3개월 동안의 자료에 해당된다. 본 연구에서는 한반도에서 발생한 지진으로 공간범위를 한정하고, 지진자료에 대한 기본적인 통계분석을 실시하고, Richter 규모로 제시되는 지진규모 수치를 이용하여 극치해석을 수행하였다. 연간 지진발생회수는 뚜렷한 증가양상을 보이고 있으나, 1978년부터 1998년 동안은 Analogue 관측기간으로 연간 발생회수는 평균 20회 정도이며, Digital 관측이 수행된 1999년 이후의 연간 발생회수는 평균 48회, 다수의 여진이 발생한 2016년 자료를 추가하는 경우에는 평균 58회 정도 발생하고 있다. 관측방법이 다른 1999년 이전 자료와 다른 연도와는 유별나게 다수의 지진이 발생한 2016년(227회), 2003년(93회) 발생회수 자료를 제외하더라도 지진 발생회수는 95% 신뢰구간에서 증가 추세가 있는 것으로 파악되었다. 한편 3.5, 4.0 이상의 지진규모는 관측기간 동안 각각 116회, 44회 발생하였으며, 이 규모를 넘어서는 지진규모 자료를 이용하여 극치해석을 수행하였다.

2.2 지진강도의 극치해석 방법

극치해석은 하천 및 해안·항만공학 분야에서 설계 강우, 설계수위, 설계조위, 설계파고 등의 추정에 전통적으로 이용되는 방법으로, 일반적으로 매년 최대 설계변수 자료를 추출하거나 또는 유의미한 기준을 넘어서는 독립적인 사상의 설계변수 자료를 추출하여 수행한다. 설계변수의 통계적인 특성을 반영하여 설계변수의 확률분포에 적합한 분포함수를 추정하고, 설계조건에서 필요로 하는 재현기간에 대한 누적확률에 해당하는 확률변수(설계변수)를 추정하는 과정을 구성된다. 그러나 기존의 방법은 후보 확률분포를 함수를 가정하여야 하는 모수적인 방법이며, 확률변수의 도시위치의 영향을 크게 받는 단점이 있기 때문에 본 연구에서는 특정 분포함수 가정이 필요 없는 비모수적인 기법을 이용하여 극치해석을 수행하였다. 이 방법은 Jeong et al.(2013)이 설계파고 추정에 적용한 사례가 있으며, 설계변수에 대한 최적의 누적분포함수(cumulative distribution function, CDF) 추정이 가장 중요한 과정으로, 본 연구에서는 Gaussian Kernel 함수를 이용하여 최적 CDF 추정을 수행하였다. 최적 CDF 추정에서 요구되는 추정 매개변수는 Bandwidth 매개변수로 다양한 추정방법이 제시되고 있으나(Wang, 2015; Alejandro et al., 2012), 본 연구에서는 Altman & Leger 공식(Altman & Leger, 1995)을 이용하여 추정하였다.
hopt=(0.25V2/B3)1/3n−1/3
여기서, hopt =최적 Bandwidth 매개변수,
V2=ρ(K)1n(n−1)∑i=1n∑j=1n1αK(xi−xjα)(i≠j),
B3=0.25[μ2(K)]2⋅D3(F),
ρ(K)=2∫−∞∞xK(x)H(x)dx,  H(x)=∫−∞xK(t)dt,
K(x)=(1/2π)⋅exp[−x2/2],
α=n−0.3σ(xi)=n−0.3⋅min{s^,(Q3−Q1)/1.349}μ2(K)=∫x2K(x)dx
D3(F)=1n3α4∑i=1n∑j=1n∑k=1nK′(xi−xjα)K′(xi−xkα),
K′(χ) = dK(χ) ⁄ dχ이다.
이론적으로 확률밀도함수는 누적분포함수의 미분함수로 얻어지기 때문에, Kernel 함수를 이용하여 최적 추정한 지진규모 CDF 매개변수는 지진규모 확률밀도함수(probability density function, pdf) 매개변수와 이론적으로 동일하여야 하지만, 실질적으로는 목적함수의 차이 또는 추정방법의 차이로 최적 매개변수가 차이를 보이고 있기 때문에 각각의 최적 매개변수와 평균 매개변수에 대한 지진 규모 추정 결과의 차이도 분석하였다.
fM(x)=1nh∑i=1nKf(x−xih)
FM(x)=1nh∑i=1nKF(x−xih), ∂FM(x)∂x=fM(x)
여기서, fM(χ), FM(χ) 각각 지진규모의 확률밀도함수와 누적분포함수이며, n =자료의 개수, h = Bandwidth 매개변수, Kf(χ)=KF(χ)= 각각 지진규모 확률변수에 대한 Kernel Gaussian 밀도함수와 분포함수이다.
최적 CDF 추정이 완료되면, 재현기간에 대한 누적확률을 계산하고, 그 누적확률에 대한 설계변수를 추정(inverse CDF)하면 된다. 한편 추정 설계변수에 대한 신뢰구간 추정은 Monte-Carlo 기법에 근거하고 있는 Bootstrap 기법(모의회수 n = 1,000; Efron, 1979; Efron and Tibshirani, 1986)을 이용하여 추정하였다. 본 연구에서 사용한 지진규모 자료는 특정 수치를 기준으로 절단한 자료이기 때문에 연속적인 함수로 표현하는 경우 경계수치를 기준으로 대수함수 등을 이용하는 처리 기법 등이 요구된다. 그러나 본 연구에서 이용한 방법은 경계수치를 기준으로 Mirror 개념(경계를 기준으로 대칭이 되는 함수를 가정)을 도입하여 경계를 초과하는 확률을 경계이내의 확률 수치에 추가되는 확률로 처리하는 기법으로, 연속적인 확률변수로 표현되는 지진규모 자료를 특정 기준 이상의 자료만을 대상으로 하는 경우에 해당하는 절단 분포함수로 간주할 수 있다. 이 방법은 기술적인 처리기법으로 확률변수의 상한-하한 경계가 명확한 경우, 대수함수를 이용한 과도한 수학적인 처리기법보다 간편하고 효과적인 분포함수 추정결과를 제시하는 장점이 있다. 이 방법의 수학적인 표현은 아래에 제시하였으며, 대수함수기법을 이용하는 방법보다 명확한 분포형태를 제시하는 것으로 판단된다.
F(x)=1/n∑i=1nH[(x−xi)/hopt],
xB=상한 또는 하한 경계가 되는 확률변수(경계 지진규모) 수치라고 하면, 절삭(truncated) 확률밀도함수, fT(χ)와 누적 분포함수, FT(χ) 는 각각 다음과 같이 추정된다.
(1) xB =상한 경계의 경우, f(χ) for all x, 그리고 , fr(χ), x≤xB.
f(x)={fL(x),x≤xBfU(x),x≥xB, fL(xB)=fU(xB),
fU(χ)함수에 대응하는 Mirror 함수를 fUm(χ), x≤xB라고 하면, fUm(xB+α)=fU(xB+α), α≥0 조건을 만족하고, fT(χ)=fL(χ)+fUm(χ), x≤xB.
절삭 누적 분포함수(fT(χ), x≤xB)도 동일한 과정을 거쳐, 동일한 형태로 변환하면 다음과 같은 분포함수가 얻어진다.
FT(x)=FL(x)+FUm(x),  x≤xB.
(2) xB =하한 경계의 경우, f(χ) for all x, 그리고 fT(χ), x≤xB.
f(x)={fL(x),x≤xBfU(x),x≥xB,  fL(xB)=fU(xB),
fL(χ) 함수에 대응하는 Mirror 함수를 fLm(χ), x≥xB 라고 하면, fLm(xB+α)=fL(xB-α), x≥xB 조건을 만족하고, fL(χ)=fLm(χ)+fU(χ), x≥xB.
절삭 누적 분포함수(FT(χ),x≥xB)도 동일한 과정을 거쳐, 동일한 형태로 변환하면 다음과 같은 분포함수가 얻어진다.
FT(x)=FLm(x)+FU(x),  x≥xB.
본 연구의 경우, 절삭 경계수치는 하한 경계(xB=2.0)에 해당한다. 인위적인 절삭이기 때문에 연속적인 함수보다는 절삭경계에서 불연속성을 보이는 것이 보다 적절하다고 할 수 있다.

3. 분석결과 및 토의

3.1 지진 규모의 기본적인 통계정보 및 분포함수 추정, 추세분석

지진규모 변수에 대한 Kernel 함수를 이용한 분포 추정 결과와 Mirror 개념을 이용하여 절삭 분포함수를 추정한 결과, 절삭 분포함수가 적절하게 추정되고 있는 것으로 파악되었다(Fig. 1 참조). 추정 분포함수의 K-S 검정 결과, 5% 유의수준에서 “관측 자료의 분포함수와 Kernel 분포함수가 같다.”는 가설을 기각할 수 없는 것으로 파악되었다(p-value = 0.34). 따라서 본 연구에서는 지진규모 변수의 신뢰구간 추정을 위하여 필요한 지진규모 난수발생은 Kernel 분포함수를 이용하여 수행하였다.

3.2 극치분석, 신뢰구간 추정

극치분석은 지진규모 3.5 이상, 4.0 이상의 조건을 만족하는 자료를 이용하여 각각 수행하였으며, 재현기간에 따른 최적 추정결과와 신뢰구간은 다음과 같다. 신뢰구간 추정은 50%(상한-하한 25%), 90%(상한-하한 5%) 조건에서 추정하였으며, 신뢰구간 추정은 추정된 CDF를 기반으로 난수를 발생하여 수행하였다.
재현기간에 대한 설계 지진규모는 규모 3.5 이상, 4.0 이상 자료를 사용한 경우와 차이를 보이는 것으로 파악되었다 (Fig. 2 참조). 평균 추정규모는 지진규모 3.5 이상의 자료를 사용한 경우가 지진규모 4.0 이상의 자료를 사용한 경우보다 재현기간 50년을 기준으로 약 2%정도 작아, 미미한 차이를 보이는 것으로 파악되었다(Table 1 참조). 재현기간 10, 50, 100년의 경우 그 차이는 각각 0.11, 0.14, 0.16으로 규모 4.0이상의 자료를 사용한 경우의 추정 지진규모가 크게 나타났으며, 그 차이는 재현기간이 증가할수록 증가하는 경향을 보이는 것으로 파악되었다.
한편 추정 설계규모의 신뢰구간도 신뢰수준이 증가할수록 증가하는 경향을 보이고 재현기간 100년의 경우, 신뢰수준 50%, 90% 조건에서 각각 0.30-0.35, 0.66-0.67 범위로 재현기간이 증가할수록 신뢰구간도 점차 완만하게 증가하는 경향을 보이는 것으로 파악되었다. 본 연구에서 사용한 기법을 이용하여 재현기간 500년, 1,000년에 해당하는 지진 규모도 추정이 가능하지만, 일반적으로 극치해석에서는 극치분석이 사용한 자료의 관측 기간 2-3배를 크게 초과하는 경우, 신뢰수준이 크게 감소하기 때문에 본 연구에서는 재현기간 100년 정도의 추정 결과만을 분석 대상으로 사용하였다.

4. 결론 및 제언

기상청에서 제공하는 지진 자료를 이용하여 설계 규모를 극치분석을 이용하여 추정한 결과, 분석에 사용한 지진 규모 4.0이상의 자료에 대하여 재현기간 100년 조건의 평균 지진규모는 5.94로 추정되었으며, 50%, 90% 신뢰구간은 [5.79-6.09], [5.62-6.29]로 추정되었다. 그러나 본 연구에서 사용한 지진규모 자료는 약 40년 정도의 짧은 기간에 해당하는 자료이기 때문에 장기 재현빈도에 해당하는 지진규모 추정에는 한계가 있다. 또한 지진발생 위험수준도 공간적인 차이를 보이기 때문에 본 연구에서 제시한 설계 지진규모와 한반도에서의 공간적인 지진 위험 수준, 그리고 신뢰구간을 고려하여 해안 구조물의 내진설계에 적용할 필요가 있을 것으로 판단된다.

감사의 글

본 논문은 2016년 해양수산부 재원으로 한국해양과학기술진흥원의 지원(선박 및 인명 대피 지원 기술 개발, PM59460), 한국해양과학기술원 기관 고유사업(PE-99524)의 지원을 받아 수행된 연구 성과입니다. 연구 지원에 감사드립니다.

Fig. 1.
Truncated cumulative distribution function estimation of the earthquake magnitude.
jkscoe-29-1-62f1.tif
Fig. 2.
Estimation of the earthquake magnitude and their confidence intervals with the return periods.
jkscoe-29-1-62f2.tif
Table 1.
Confidence intervals of the earthquake magnitude with the return periods.
RP Earthquake Magnitude > 3.5 Case Earthquake Magnitude > 4.0 Case
L90 L50 M U50 U90 R90 L90 L50 M U50 U90 R90
5 4.85 4.96 5.03 5.11 5.20 0.35 4.92 5.02 5.09 5.17 5.26 0.34
10 5.07 5.17 5.25 5.33 5.44 0.38 5.16 5.27 5.36 5.43 5.55 0.39
15 5.16 5.27 5.37 5.45 5.61 0.45 5.28 5.39 5.48 5.57 5.71 0.43
20 5.23 5.33 5.45 5.55 5.72 0.50 5.34 5.47 5.57 5.66 5.81 0.47
25 5.27 5.37 5.50 5.62 5.80 0.53 5.39 5.52 5.63 5.73 5.90 0.50
30 5.30 5.41 5.55 5.67 5.86 0.56 5.43 5.56 5.68 5.78 5.96 0.52
35 5.32 5.44 5.59 5.71 5.90 0.58 5.46 5.60 5.72 5.83 6.01 0.55
40 5.34 5.47 5.62 5.76 5.94 0.60 5.48 5.62 5.75 5.87 6.05 0.56
45 5.36 5.49 5.65 5.79 5.97 0.61 5.50 5.65 5.78 5.90 6.08 0.58
50 5.37 5.50 5.67 5.82 5.99 0.62 5.52 5.67 5.81 5.93 6.11 0.59
55 5.38 5.52 5.69 5.84 6.01 0.63 5.53 5.69 5.83 5.95 6.14 0.60
60 5.39 5.53 5.71 5.86 6.03 0.64 5.55 5.70 5.84 5.97 6.17 0.62
65 5.40 5.54 5.72 5.88 6.05 0.65 5.56 5.72 5.86 6.00 6.19 0.63
70 5.41 5.55 5.73 5.89 6.06 0.65 5.57 5.73 5.88 6.01 6.21 0.63
75 5.42 5.56 5.74 5.90 6.08 0.66 5.58 5.75 5.89 6.03 6.22 0.64
80 5.42 5.57 5.75 5.92 6.09 0.66 5.59 5.76 5.90 6.04 6.24 0.64
85 5.43 5.57 5.76 5.93 6.10 0.67 5.60 5.77 5.91 6.06 6.25 0.65
90 5.44 5.58 5.77 5.94 6.11 0.67 5.61 5.78 5.92 6.07 6.27 0.66
95 5.44 5.59 5.78 5.94 6.11 0.67 5.62 5.78 5.93 6.08 6.28 0.66
100 5.45 5.60 5.78 5.95 6.12 0.67 5.62 5.79 5.94 6.09 6.29 0.66

* RP = return periods(years), M = mean of the estimated magnitude, L50, U50 = lower and upper limits of the 50% confidence level, respectively; L90, U90 = lower and upper limits of the 90% confidence level, respectively.

References

Jeong, WM, Cho, HY, Kim, GW (2013). Analysis of Confidence Interval of Design Wave Height Estimated Using a Finite Number of Data, J. of Korean Society of Coastal and Ocean Engineers, 25(4):191-199 (in Korean).
crossref
Korea Meteorological Administration. (2016). www.kma.go.kr.

Altman, N, Leger, C (1995). Bandwidth selection for kernel distribution function estimation, J. of Statistical Planning and Inference, 46, 195-214.
crossref
Alejandro, Q-del-R, Graciela, E-P (2012). Nonparametric kernel distribution function estimation with kerdiest: An R package for bandwidth choice and applications, J. of Statistical Software, 50(8):1-21.

Wang, XF. (2015). Nonparametric Smooth ROC Curves for Continuous Data, R Package ‘sROC’, 1–14, https://cran.r-project.org/web/packages/sROC/sROC.pdf (Accessed 11 Nov., 2016).

Kim, SH, Lee, J-H, Kim, DK (2005). Probabilistic Seismic Risk Analysis of Breakwater Structures, J. of J. of Korean Society of Coastal and Ocean Engineers, 17(1):32-40 (in Korean).

Shin, JY, Kim, T-W, Song, H-Y, Kwon, HH. (2013). Application of Mixed Distribution to Statistical Frequency Analysis of earthquake Data at East Sea, Conference of the Korean Society of Civil Engineers. 1891-1894.

Efron, B (1979). Bootstrap Methods: Another Look at the Jackknife, The Annals of Statistics, 7(1):1-26.
crossref
Efron, B, Tibshirani, R (1986). Bootstrap Methods for Standard errors, Confidence Intervals, and Other Measures of Statistical Accuracy, Statistical Science, 1(1):54-77.