1. 서 론
시간의 진행에 따라 대부분의 사회기반시설은 노령화되면서 그 성능이 감소하게 된다. 성능 감소는 해당 시설물의 사용성이나 안정성에 중대한 영향을 미치게 된다. 특히 사회기반시설의 경우 파괴에 따른 사회적 영향 정도와 경제적 손실이 크다. 따라서 해당 시설물이 파괴되기 전에 예방적으로 유지관리 하는 것이 필요하다. 미국이나 일본 등의 선진국은 지난 수 십년 동안 사회기반시설물의 유지관리에 많은 예산을 투입하여 왔으며, 그 예산 규모도 점점 증가하는 추세를 보이고 있다. 이는 저출산 고령화 사회에서 경제발전을 지속적으로 유지하기 위해서는 먼저 노후화된 사회기반시설을 젊게 만드는 작업이 중요하다는 관점에서 접근하고 있기 때문이다. 우리나라도 사회적으로는 저출산, 고령화가 진행되고 있고, 구조적으로는 지난 세기에 건설된 사회기반시설들이 그 내구년수에 도달하고 있다. 또한 아직도 경제성장을 견인할 많은 신규 사회기반시설물에 대한 투자를 계속하고 있어 시간이 진행됨에 따라 고령화되는 시설물들은 점점 쌓여질 수 밖에 없다. 또한 외부 환경변화에 따른 사회의 기대 요구성능도 높아지고 있다. 따라서 우리나라에서도 시간이 갈수록 사회기반시설물에 대한 유지관리 비용이 큰 폭으로 증가할 것이다. 따라서 유지관리와 관련된 결정요소들을 최적화할 수 있는 공학적 기법을 개발할 필요가 있다. 유지관리에 소요되는 비용은 최소화하면서 그에 따른 편익, 성능향상을 최대화할 수 있는 기법을 개발하여야 한다.
BS3811(1984)에 의하면 유지관리(maintenance)란 사용년수 동안 구조물에 요구되는 기능이 올바로 수행될 수 있도록 보수보강하거나 파괴된 경우 복구하는 기술적·행정적 관련 행위들이라 정의하고 있다. 이상의 정의에 의하면 구조물의 피해도를 시간의 진행에 따라 확률적으로 추적할 수 있는 모형이 절대적으로 필요하다. 구조물의 안전성에 지대한 영향을 주는 임의의 파괴모드에 대한 과거 점검 자료를 기반으로 미래의 구조물 피해를 예측하는 것이다. 이 과정에 필연적으로 불확실성이 포함될 수밖에 없다. 이와 같은 불확실성은 다음과 같이 두 가지로 구분된다. 하나는 과거 자료가 가지는 불확실성(sampling uncertainty)이고 다른 하나는 시간의 진행에 따라 발생하는 불확실성(temporal uncertainty)이다. 현재 시설물의 시간에 따른 피해도를 확률적으로 해석하는데 가장 일반적으로 사용하는 방법이 피해율만을 확률변수로 고려하는 피해율 모형(random damage rate model)이다. 시간의 진행에 따른 피해도가 피해율에 전적으로 의존하여 멱법칙(power law)과 같이 정의된 시간의 함수로 거동한다고 가정하는 방법이다. 따라서 피해율에 대한 통계적 특성 및 확률적 거동특성을 올바로 알아야 한다. 그러나 기계적 장치와는 다르게 토목 시설물들에 대하여는 피해율에 대한 자료를 얻는 것이 상당히 어렵다. 또한 토목 구조물은 여러 요소들의 상호작용에 의하여 성능이 발휘되기 때문에 시간의 진행에 따른 피해율의 통계적 특성 및 확률적 거동특성도 일정하지도 않을 수 있다. 설령 피해율 자료를 얻는다 하더라도 임의의 고정된 시간에 대한 자료일 뿐이다. 따라서 시간의 진행에 따라 다르게 발생할 수 있는 불확실성을 고려할 수 없다(Pandey et al., 2009). 이와 같은 시간에 따른 불확실성을 올바로 고려할 수 있는 가장 효율적인 방법이 추계학적 확률과정(stochastic process)을 이용하는 것이다(Noortwijk, 2009). 추계학적 확률과정 이론은 경제학이나 산업공학 등의 분야에서 시간에 따른 제반 현상을 확률적으로 연구하는데 많이 활용되고 있다. 현재까지 개발된 추계학적 확률과정을 크게 분류하면 WP/LP(Wiener Process/Levy Process), GP(Gamma Process), 그리고 CPP(Compound Poisson Process) 등 으로 구분할 수 있다. 아직 항만분야에서 이에 대한 연구가 대단히 제한적인 수준에 머물고 있다. 장래 사회기반시설물의 안전에 대한 사회적 요구수준이 향상될 것이고 자연환경이 과거와는 다르게 변할 가능성이 높다. 따라서 이와 같은 영향을 고려하여 새로운 구조물을 설계하거나, 기존 구조물을 올바로 유지관리하기 위해서는 피해도를 시간에 따라 추적할 수 있는 추계학적 확률과정에 대한 연구가 필요하다.
Ellingwood and Mori(1993), Frangopol et al.(2004), Pandey et al.(2009) 등이 피해율 모형을 이용하여 시간에 따른 구조물의 피해와 관련된 확률론적 해석을 수행하였다. 그러나 단일 피해경로에 대한 해석이라는 한계성을 갖게 된다. 이와 같은 문제를 해결하기 위하여 Doksum and Normand(1995), Whitmore(1995), Basu and Lingham(2003) 등이 WP 모형에 대한 연구를 수행하였다. 또한 Noortwijk(1995), Singpurwalla(1997), Weide(1997), Heutink et al.(2004) 등이 WP 모형의 문제점을 언급하면서 그 대안으로 GP 모형을 제시하였다. 마지막으로 Nakagawa(2010), Weide et al.(2010), Weide and Pandey(2011) 등이 CPP 모형에 대한 연구를 수행하였다. 이상에 언급한 연구들은 단지 각 추계학적 확률과정이 갖는 수학적 특성을 해석한 것이지 사회기반 시설물에 대한 적용을 다룬 것은 아니다. 특히 추계학적 확률과정을 이용하여 항만 구조물의 시간에 따른 피해도를 추정한 연구는 수행되지 못하고 있다. 따라서 본 연구에서는 항만의 외곽시설 중 한 형식인 경사제 피복재의 시간에 따른 피해도를 추계학적 확률과정을 이용하여 해석하고자 한다. 특히 MCS(Monte-Carlo Simulation) 기법을 이용하여 시간에 따른 피해 경로를 직접 추적하였다. 또한 누적 피해도의 시간에 따른 분포함수와 한계수준에 따른 파괴확률도 산정할 수 있었다. 경사제 피복재의 시간에 따른 피해 경로와 분포함수 추정은 기존의 경사제 피복재를 예방적으로 유지관리하는데 중요할 뿐만 아니라 새로운 경사제 설계시 생애주기 기반 최적 설계에 반드시 필요하다.
제 2절에 구조물의 누적 피해도를 해석하기 위한 WP, GP 그리고 CPP의 추계학적 확률과정에 대한 수학적 정의와 각 모형의 특성과 차이점을 설명하였다. 제 3절에서는 각각의 추계학적 확률과정을 이용하여 누적 피해도의 선형적, 비선형적 거동특성을 해석하였다. 특히 MCS 기법을 이용하여 피해도의 경로를 직접 추적하였다. 또한 누적 피해도의 시간에 따른 분포함수와 한계수준에 따른 파괴확률도 산정하였다. 또한 제 4절에서는 표본경로기법을 개발하여 추계학적 확률과정을 경사제 피복재에 적용할 수 있는 방법을 제시하였다. 마지막으로 제 5절에 결론을 언급하였다.
2. 누적 피해도 추적을 위한 추계학적 확률과정
추계학적 확률과정의 수학적 정의를 제시하기 전에 먼저 이해를 도모하기 위하여 현재 시설물의 시간에 따른 누적 피해도를 확률적으로 해석하는데 가장 일반적으로 사용하는 방법, 피해율만을 확률변수로 고려하는 경험적 방법을 설명하였다. 이와 같은 피해율 모형에서는 구조물의 시간에 따른 누적 피해도, X(t)를 다음 식 (1)과 같이 정의한다.
여기서 A는 피해율로 임의의 분포함수를 따르는 확률변수이다. Λ(t)는 경험적으로 결정되는 시간의 함수로 p = 1.0인 경우를 선형 모형(linear/additive model)이라 하고 p ≠ 1.0인 경우를 비선형 모형(nonlinear model)이라 한다. 비선형 모형은 다시 p > 1.0 인 경우의 가속 모형(accelerated model)과 0.0 < p < 1.0 인 경우의 포화 모형(saturated model)으로 구분된다. 따라서 누적 피해도의 변동계수, VX(t)는 다음 식 (2)와 같이 피해율의 변동계수, VA=σA/μA와 같게 된다. 여기서 μA와 σA는 각각 피해율에 대한 평균과 표준편차이다.
식 (2)는 모든 시간에서 누적 피해도의 변동계수가 일정하다는 것을 의미한다. 그러나 실제에서는 시간에 따른 누적 피해도의 불확실성이 일정하지 않을 수 있다. 이와 같은 문제, 시간에 따라 변하는 불확실성을 고려하기 위하여 개발된 확률적 해석모형이 추계학적 확률과정이다. 추계학적 확률과정은 일반적으로 WP, GP, 그리고 CPP로 구분할 수 있다. 아래에 각 추계학적 확률과정의 수학적 정의를 제시하였다.
2.1 Wiener 확률과정
먼저 WP에 대한 수학적 정의이다. 시간에 따른 구조물의 누적 피해도는 다음 식 (3)과 같이 정의된다(Nicolai, et al, 2007).
특히 식 (3)에서 W[Λ(t)]를 표준화된 WP라 하고 다음의 조건을 반드시 만족하여야 한다. 먼저 W(0) = 0이고, 0 ≤ t1 ≤ t2 ≤ T인 경우 W[Λ(t2)]-W[Λ(t1)]는 정규분포, N[0, Λ (t2) - Λ(t1)]을 따른다. 마지막으로 0≤t1<t2<t3<t4≤T의 경우 W[Λ(t2)]-W[Λ(t1)]와 W[Λ(t4)]-W[Λ(t3)]는 서로 독립이다.
WP의 확률적 특성을 살펴보면 시간에 따른 누적 피해도는 두 번째 가정에 의하여 다음 식 (4)를 만족한다.
여기서 N(μ, σ2)은 평균 μ와 분산 σ2을 갖는 정규분포를 의미한다. 따라서 WP에서는 시간에 따른 누적 피해도의 변동계수,
V X t = 1 / ν t
또한 p = 1.0의 경우 식 (3)의 누적 피해도가 임의의 한계수준, α를 최초로 통과하는 시간 TX (α), 즉, 구조물의 내구년수의 분포함수는 P[TX(α) ≤ t] = P[X(t) ≥ α]에 의하여 다음 식 (5)와 같이 정의된다.
여기서 Φ(x)는 표준정균분포의 누적분포함수이다, p ≠ 1.0인 경우에 대하여도 식 (5)를 동일하게 적용할 수 있다. 따라서 식 (5)를 이용하면 임의의 시간 간격, 예로 t-1년과 t년 사이에 누적 피해도가 임의의 한계수준을 최초로 통과할 확률은 다음 식 (6)과 같이 정의된다.
그러나 WP는 두 번째 조건에 따라 시간의 진행에 따라 누적 피해도가 반드시 증가하는 것이 아니라 감소할 수도 있다는 특징을 가진다. 이와 같은 특징을 구조물의 시간 진행에 따른 누적 피해도의 물리적 특성과 비교해 보면 구조물의 누적 피해도가 어느 순간에는 저절로 치유되어 회복된다는 의미이다. 실제 항만 구조물에서는 발생될 수 없는 물리적 현상이다. 실제 구조물은 시간의 진행에 따라 누적 피해도가 항상 증가하기 때문이다. 이와 같은 문제를 해석하기 위하여 도입된 개념이 GP이다.
2.2 Gamma 확률과정
RP(Renewal Process)는 일정한 시간동안 발생하는 사상(events)의 확률적 거동특성을 해석하는 개념이다. 이 개념에 의하면 내부도착시간(inter-arrival time)이 일정 도착강도를 갖는 지수분포를 따르는 확률변수이면 일정 시간에 도착한 시간(arrival time)의 분포함수는 감마분포를 따른다. GP에서는 이와 같은 확률적 개념을 이용하여 누적 피해도가 다음 식 (7)과 같이 정의되는 감마분포(gamma/Erlang distribution)를 따른다고 가정한다(Noortwijk, 2009).
일반적으로 v(t)를 형상계수, u를 축척계수라 한다. 누적 피해도가 GP를 따르기 위해서는 반드시 다음 조건을 만족하여야 한다. 먼저 X(0) = 0.0이고, 0≤t1<t2의 경우 X(t2)-X(t1)~Ga[x|v(t2-v(t1), u] 이다. 마지막으로 X(t)는 독립적인 증가를 갖는다. 따라서 GP에서 누적 피해도의 변동계수,
V X t = 1 / ν t
따라서 형상계수함수와 축척계수를 결정하여야 한다. 비교 목적으로 본 논문에서는 다음과 같은 두 가지 방법을 제시하였다. 하나는 모멘트법(method of moment)을 이용하여 WP의 통계적 특성과 비교하는 방법이다. 즉, 식 (4)의 평균과 분산이 각각 식 (7)의 평균 및 분산과 동일하다고 가정하면 다음 식 (8)을 얻을 수 있다.
그러나 WP는 순간 피해도가 증가 또는 감소할 수 있는데 비해 GP에서는 식 (7)에 의하여 증가만 할 수 있다. 또한 WP에서는 시간에 따른 누적 피해도가 연속이라고 가정하는데 비해 GP는 누적 피해도가 우극한을 갖는 부분연속(piecewise continuous)이라고 가정한다.
다른 하나의 방법은 식 (1)의 피해율 모형과 비교하기 위한 방법이다. Pandey, et al.(2009)이 사용한 방법으로 v(t)=v0Λ(t)를 만족한다고 가정하는 방법이다. 따라서 임의의 시간, t1에서 식 (1)의 평균과 변동계수가 식 (7)의 평균과 변동계수와 각각 동일하다고 가정하면 다음 식 (9)를 얻을 수 있다.
2.3 Compound Poisson 확률과정
마지막으로 CPP에 대한 수학적 정의이다. CPP에서는 하중 발생사상을 Poisson 확률과정으로 고려하는 대신, 각 하중에 의하여 발생한 개별 피해는 임의의 분포함수로 고려한다는 점이 GP와 다르다. 누적 피해도는 RP 개념에 의하여 다음 식 (11)과 같이 각각의 하중에 의하여 발생한 개별 순간피해도, 의 합으로 정의된다(Barlow and Proschan, 1965; Karlin and Taylor, 1975; Ross, 1970, 1980).
식 (11)의 누적 피해도가 CPP가 되기 위해서는 다음의 조건을 반드시 만족하여야 한다. 먼저 t시간 동안 발생되는 하중의 개수, N(t)는 Poisson 확률과정을 따른다. 또한 Yj는 임의의 독립적이며 동일한 분포(independent and identically distribution)를 따르는 확률변수이다. 마지막으로 N(t)와 Yj는 서로 독립이다.
만약 Yj가 임의의 분포함수 FY(y)를 따른다면 N(t) = n의 하중발생에 의한 누적 피해도 X(t) ≡ Xn~
F Y n x
또한 식 (11)에서 P[N(t) = j]가 하중발생강도 μ를 갖는 HPP(Homogeneous Poisson Process)를 따르고 Yj가 피해강도함수 λ(x) = axb를 갖는 지수분포를 따르면 누적 피해도에 대한 n차 모멘트는 다음 식 (13)과 같이 유도된다(Weide and Pandey, 2011).
식 (13)은 피해율이 일정하지 않은 경우에도 해석할 수 있다. 따라서 식 (13)을 이용하면 누적 피해도의 시간에 따른 불확실성, VX(t) = {E[X(t)2]–E[X(t)2]} ⁄ E[X(t)]을 쉽게 산정할 수 있다.
이상과 같이 시간에 따른 누적 피해도를 해석할 수 있는 CPP를 수립하였다. 따라서 CPP와 GP의 차이를 다음과 같이 두 가지로 설명할 수 있다. 하나가 임의의 유한한 기간 동안 발생되는 하중 발생과정을 각기 다르게 고려한다는 점이고, 다른 하나는 GP에서는 시간에 따른 누적 피해도를 감마분포로 가정하는데 비해 CPP에서는 임의의 분포함수로 정의할 수 있다는 점이다.
3. 누적 피해도의 시간에 따른 경로 추적
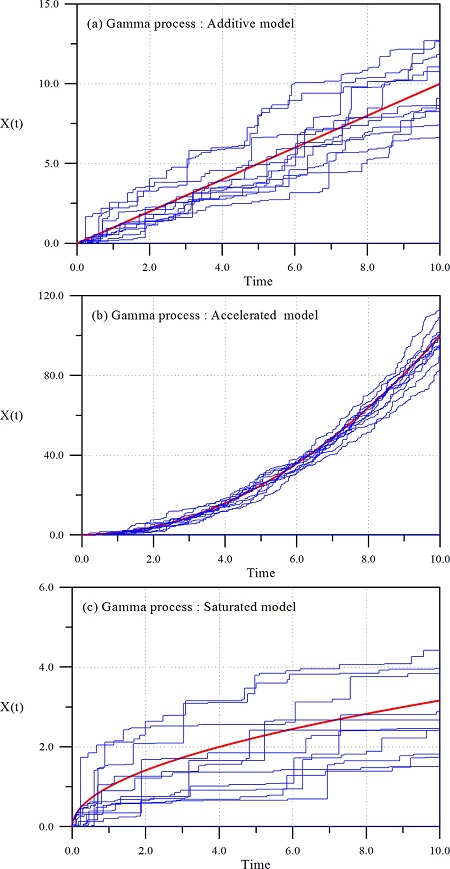
누적 피해도의 시간에 따른 거동특성을 확률적으로 해석하기 위하여 모두 네 개의 모형이 수립되었다. 하나는 피해율 모형이고 나머지는 추계학적 확률과정 모형이다. 특히 본 연구에서는 멱함수 형태의 시간함수, Λ(t) = tp를 도입하여 기존의 대부분의 연구들이 수행한 선형적 연구(p = 1.0)들을 확장할 수 있었다. 따라서 아래에 p의 변화에 따른 누적 피해도의 선형 거동특성 뿐만 아니라 비선형 거동특성을 추적하였다. 또한 각각의 경우에 대하여 유지관리의 최적화 해석에 반드시 필요한 임의의 한계수준, α에 대한 내구년수의 분포함수를 비교하였다. 여기서 WP와 GP는 시간에 따른 누적 피해도의 진행 경로 하나 하나를 직접 추적하면서 내구년수의 분포함수 등의 확률적 특성을 해석하는데 비해 피해율 모형과 CPP는 누적 피해도의 평균을 산정하고 내구년수의 분포함수를 해석하는 개념이다.
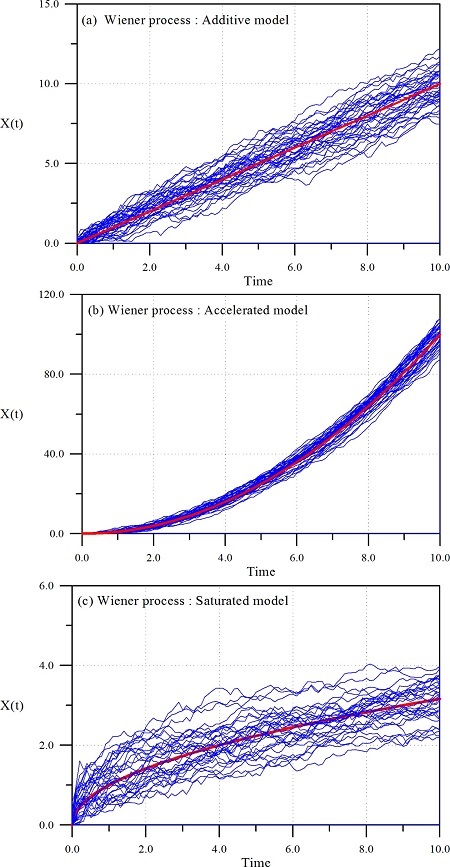
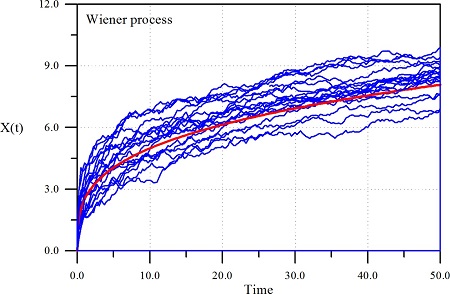
먼저 μA = 1.0, VA = 0.5에 대하여 p = 1.0, p = 2.0 그리고 p = 0.5에 대하여 식 (3)의 WP로 추적된 누적 피해도의 피해경로를 Fig. 1에 제시하였다. 그림에는 식 (1)에 의하여 산정된 누적 피해도의 평균도 함께 제시하였다. 그림에서 알 수 있듯이 시간의 진행에 따른 누적 피해도의 불확실성이 변하는 것을 확인 할 수 있다. 이는 식 (1)의 피해율 모형에서는 고려할 수 없는 현상이다. 또한 누적 피해도의 한 경로를 따라가다 보면 임의 시간의 누적피해도가 그 이전 시간의 누적 피해도 보다 작아지는 경우가 발생하고 있다. 다양한 조건에서 해석한 결과에 의하면 이와 같은 경향은 p ≤ 1.0면서 μA가 작고 VA가 큰 경우에 발생한다. 따라서 WP를 구조물의 누적 피해도에 적용하기 위해서는 이와 같은 특징에 주의하여야 한다.
비록 누적 피해도의 통계적 특성이 동일하더라도 시간함수, Λ(t)의 p에 따라 누적 피해도의 피해경로가 상당히 다르게 진행하고 있다. 따라서 임의 구조물의 시간에 따른 누적 피해도를 올바로 예측하기 위해서는 누적 피해도의 통계적 특성 뿐만 아니라 시간함수의 p를 올바로 결정하여야 한다. 예로 철근의 부식에 따른 콘크리트 강도의 시간에 따른 감소의 경우는 p = 1.0인데 비해 황산염분의 침투에 따른 강도감수의 경우에서는 p = 2.0으로 알려지는 등 구조분야에서는 파괴모드에 따른 연구가 활발히 진행되고 있다(Ellingwood and Mori, 1993). 그러나 항만 구조물에 대해서는 그 필요성에도 불구하고 이에 대한 연구가 활발히 이루어지지 못하고 있다. 이는 상당한 실험적 노력이 필요하기 때문이다.
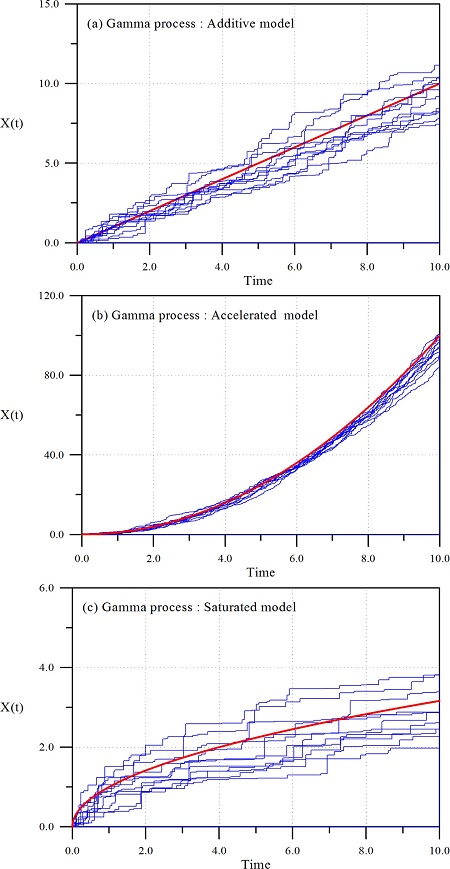
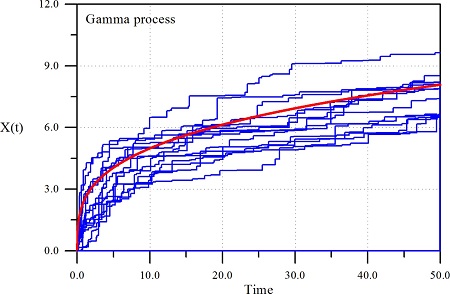
다음으로는 비교의 목적으로 WP와 동일조건에 대하여 GP로 해석한 결과를 Fig. 2에 제시하였다. 식 (7)의 매개변수, v(t)와 u는 식 (8)을 이용하여 결정하였다. 해석 결과에 의하면 전반적인 거동특성이 WP와 유사하고 식 (7)에서 언급한 제반 성질을 잘 만족하고 있다. 특히 그림에서 알 수 있듯이 WP의 결과와 동일하게 시간의 진행에 따른 누적 피해도의 불확실성이 변하는 것을 확인 할 수 있다. 그러나 두 결과를 비교하면 GP가 WP가 보다 약간 작게 누적 피해도를 추정한다. 또한 GP의 각 경로를 추적하면 WP와는 다르게 임의 시간의 누적피해도가 그 이전 시간의 누적 피해도 보다 항상 크다. 이는 GP가 구조물의 누적 피해도를 해석하는데 WP보다 물리적 현상을 더 잘 만족한다는 의미이다. GP가 현재 구조물의 시간에 따른 누적 피해도의 경로를 추적하는데 가장 많이 사용되고 있는 이유이다. 이상과 같이 WP와 GP를 MCS 기법과 접목하여 시간에 따른 누적 피해도의 경로를 추적할 수 있었다. 기존의 피해율 모형을 해석하는데 필요한 자료만 가지고도 시간에 따른 불확실성을 올바로 고려하면서 미래 누적 피해도를 추정할 수 있었다. 따라서 이하에는 WP와 GP 그리고 CPP에 의하여 산정된 임의의 한계수준에 대한 내구년수의 분포함수를 해석하였다.
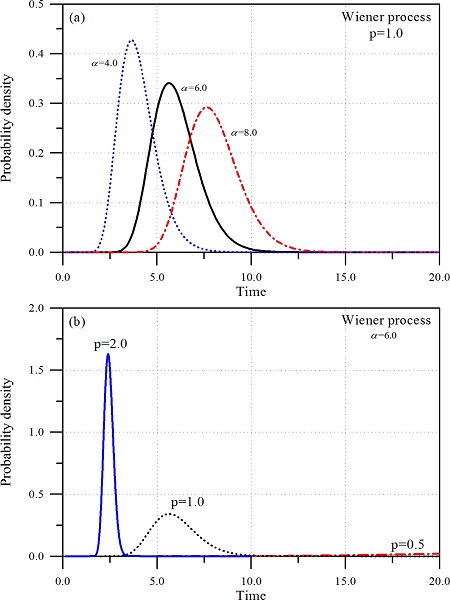
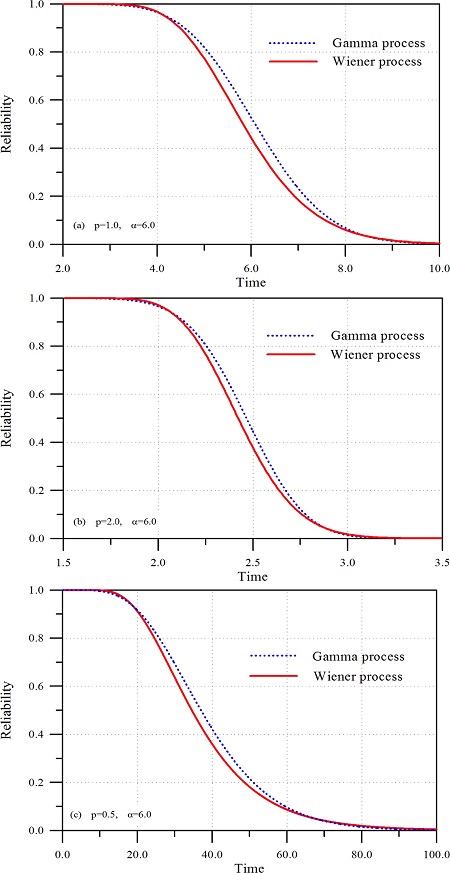
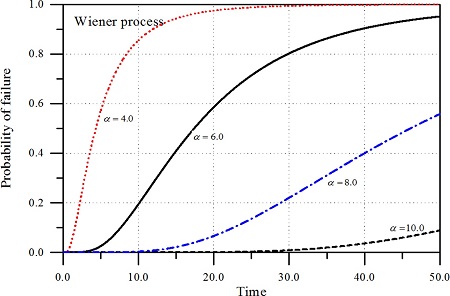
먼저 WP에 의하여 산정된 내구년수의 분포함수를 Fig. 3에 제시하였다. p와 α를 변화시키면서 해석하였다. p = 1.0의 경우에 대한 결과를 보면 한계수준이 커짐에 따라 내구년수의 분포함수가 우측으로 이동하면서 폭이 넓어진다. Fig. 1에서 쉽게 확인 할 수 있듯이 상대적으로 한계수준이 크면 그 수준에 도달하는 시간이 늦어지고 분산이 커지고 있다. 반면 α = 6.0으로 일정한 경우 p가 커짐에 분포함수는 좌측으로 이동하고 폭이 좁아진다. 누적 피해도가 일찍 한계수준에 도달하면서 분산이 작아진다. 또한 GP에 의하여도 내구년수의 분포함수가 산정되었다. 전반적인 경향은 WP의 결과와 유사하지만 통계적 특성들이 약간 다르다. 자세히 비교하기 위하여 Fig. 4에 두 결과를 비교하였다. Fig. 4는 시간에 따른 구조물의 신뢰도를 산정한 것이다. GP가 WP보다 누적 피해도를 약간 작게 추정하기 때문에 GP에 의한 결과가 WP의 결과보다 약간 안전한 것으로 나타나고 있다.
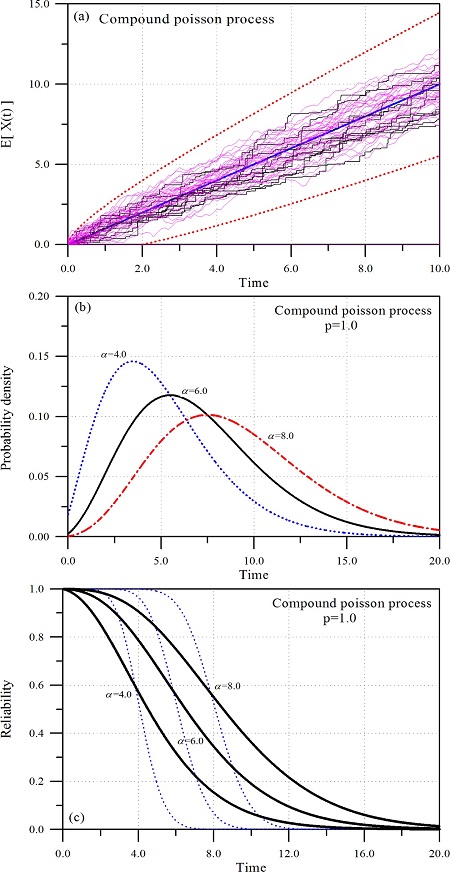
마지막으로 CPP에 의한 결과를 Fig. 5에 제시하였다. a = 1.0, b = 0.0에 대하여 시간에 따른 누적 피해도의 평균과 분산 그리고 한계수준에 따른 내구년수의 분포함수와 구조물의 신뢰도이다. 식 (13)과 식 (15)는 하중의 발생과정을 HPP로 가정하였기 때문에 p = 1.0에 대한 것이다. 또한 비교의 목적으로 단위시간당 하나의 하중이 발생한다고 가정하였다. 먼저 Fig. 5(a)에 시간에 따른 누적 피해도의 평균을 제시하였다. 그림에서 점선은 μX(t) ± σX(t)이며, 비교 목적으로 동일 조건에 대한 WP와 GP의 결과도 함께 제시하였다. 그림에서 쉽게 알 수 있듯이 CPP는 WP나 GP 보다 시간에 따른 누적 피해도의 변동계수를 상당히 크게 산정한다. 따라서 Fig. 5(b)에 제시된 내구년수의 분포함수도 상당히 넓은 범위에 걸쳐 나타나고 있다. 마지막으로 Fig. 5(c)에 CPP에 의하여 산정된 구조물의 신뢰도를 WP 및 GP의 결과와 비교하였다. WP나 GP와는 다르게 전반적으로 완만하게 변하며, 해당 한계수준을 기준으로 좌우의 거동특성이 완전히 다르게 나타나고 있다. 좌측영역에서는 신뢰도를 작게, 우측영역에서는 신뢰도를 크게 산정하고 있다.
이상의 결과는 식 (1)에 정의된 피해율의 통계적 특성을 알고 있다는 가정하에 얻어진 결과이다. 따라서 여러 번의 점검을 통하여 균일한 많은 자료를 얻을 수 있을 때만 해석이 가능하다. 그러나 이와 같은 자료를 확보하는 것은 상당히 어렵다. 실제 대부분의 구조물들에서는 시특법 등과 같은 법령에 따라 정해진 일정 시간간격으로 점검을 실시하고 그때까지의 누적 피해도를 관측하게 된다. 따라서 이하에서는 단 한 번의 점검이 이루어진 구조물에 대하여 시간에 따른 누적 피해도를 추적하기 위한 추계학적 확률과정 적용 방법을 설명하고자 한다. 상당히 제한적인 피해율 자료를 이용하여 누적 피해도의 경로를 추적하는 방법이다. 이 경우는 점검이 이루어진 시간이 해석에서 고려되어야 한다. 앞에서 설명한 추계학적 확률과정 중 GP만이 이를 해석할 수 있다.
이에 대한 해석을 위해 본 연구에서는 t1 = 3.0에서 정밀 점검이 실시되어 그 때까지의 누적 피해도를 관측했다고 가정하였다. 비교 목적으로 누적 피해도로부터 산정된 피해율, X(t1)/t1의 통계적 특성이 μA = 1.0, VA = 0.5라고 가정한 경우이다. 따라서 식 (8)이 아니라 식 (9)를 이용하여 매개변수를 결정하여야 한다. GP를 이용하여 시간에 따른 누적 피해도의 경로 추적 결과를 Fig. 6에 제시하였다. Fig. 2와 비교하면 누적 피해도의 경로의 변동 폭이 훨씬 크다는 것을 알 수 있다. 수학적으로 보면 시간에 따른 누적 피해도의 변동계수가 Fig. 2의 결과보다
Λ t 1
4. 경사제 피복재에의 적용
추계학적 확률과정을 이용하여 임의 구조물의 시간에 따른 누적 피해도를 직접 추적할 수 있는 방법을 자세히 설명하였다. 따라서 본 절에서는 이상의 해석 결과를 바탕으로 경사제 피복재의 누적 피해도를 직접 추적하고자 한다. WP와 GP를 이용하여 경사제 피복재의 시간에 따른 누적 피해도를 추적하기 위해서는 먼저 피해율에 대한 통계적 특성을 알아야 한다. 이를 위해서 본 연구는 다음에 설명하는 표본경로기법(sample path method)을 개발하였다.
먼저 경사제 피복재의 피해를 정의하기 위하여 본 연구에서는 Van der Meer(1988)가 제안한 다음 식 (17)의 피해수준(damage level)을 사용하였다(PIANC, 1992).
여기서 Ae와 Dn은 각각 피복재의 피해면적(eroded crosssectional area)과 대표직경(nominal diameter)이다. 일반적으로 식 (17)의 피해수준, S는 피복재의 단위중량, 투과계수, 제체의 기울기 등의 기하학적, 물리적 특성과 내습하는 파랑, 즉, 유의파고, Hs와 평균주기, Tm 그리고 파랑의 지속시간 등에 의존한다. Melby(1999, 2005)는 다음 식 (18)의 경험식을 사용하여 각기 다른 크기를 갖는 연속적인 하중이 내습할 때 시간, t에 따른 기대 피해수준,
S ¯
여기서 Ns = Hs/ΔDn, Δ = γs/γw-1, γs와 γw는 각각 피복재와 해수의 단위중량이다. 또한 Tm은 평균주기 그리고 경험상수 as = 0.025, bs = 0.25이다. 식 (18)의 경험식을 이용하여 추정한 기대 누적 피해도 결과를 Fig. 8에 제시하였다. Melby(1999)의 실험자료 Series B'과 C'에 대한 결과이다. 그림에서 볼 수 있듯이 식 (18)에 의하여 추정된 결과가 실험자료들과 잘 일치하고 있다. 특히 연속적인 하중의 내습에 따라 경사제 피복재의 기대 누적 피해도는 선형이 아닌 비선형, 즉, 포화 거동특성을 따른다는 것이다. 따라서 본 연구에서도 식 (18)을 이용하여 태풍의 내습에 따른 기대 누적 피해도의 거동특성을 해석하였다.
Fig. 8.
Comparison of the estimated results of expected cumulative damage level with the experimental results.

Burcharth(1992)가 해석한 임의의 경사제 단면 조건에 표본경로기법을 적용하여 식 (18)을 이용하여 피복재의 누적 기대 피해도를 추적하였다. 설계파고 4.4 m에 대하여 Hudson의 5% 피해율(KD = 4.0)을 기준으로 제체경사 cotα = 1.5, Δ = 1.6인 조건이다. 따라서 피복재의 직경 Dn = 1.5 m이다. 이와 같은 경사제 피복재에 매년 태풍이 연속적으로 내습하여 피해를 유발한다고 생각하였다. 내습하는 태풍은 다음 식 (19)와 같이 정의되는 년 최대 유의파고에 대한 Gumbel 극치분포를 갖는다고 가정하였다.
여기서 κ와 ξ는 각각 축척계수(scale parameter)와 위치계수(location parameter)이다. 본 연구에서는 Burcharth(1992)의 조건, κ = 1.83 m-1, ξ = 4.08 m를 사용하였다. 년 최대 유의파고의 분포함수를 이용하였다는 것은 일 년에 발생하는 태풍 중 가장 피해가 클 것으로 예상되는 최대 태풍에 의한 피해만을 고려한다는 의미이다.
표본경론기법을 수행하는 절차는 다음과 같다. 먼저 식 (19)를 이용하여 매년 발생하는 태풍의 유의파고를 MCS 기법을 이용하여 무작위로 생성한다. 다음은 Goda(2010)가 제안한 다음 식 (20)을 이용하여 주기를 계산한다.
마지막으로 식 (18)을 이용하여 Ns와
S ¯
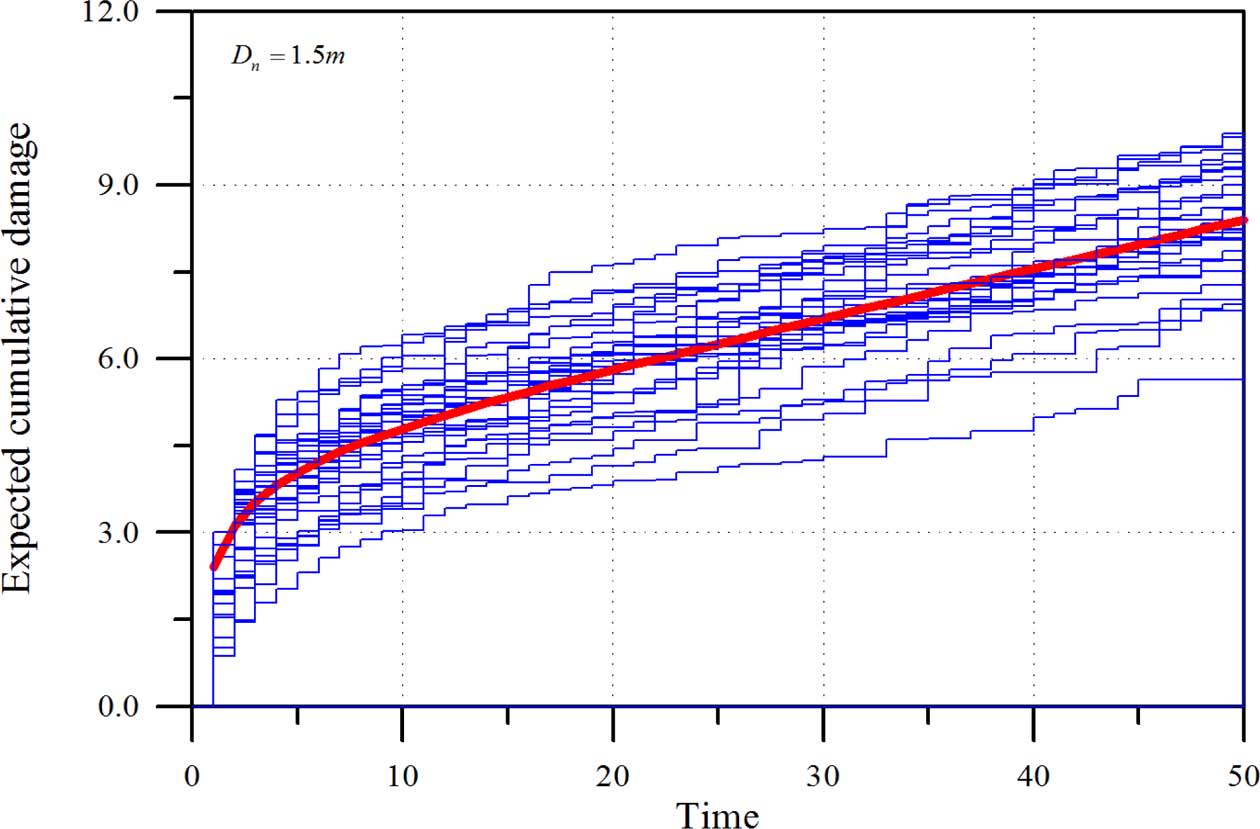
이상에 설명한 표본경로기법에 의하여 산정된 경사제 피복재의 누적 기대 피해수준의 결과를 Fig. 9에 제시하였다. 대략 1000 파가 내습한다고 생각하여 각 태풍의 지속시간을 약 3.0 시간이라고 가정하여 모두 50×10000번의 반복을 실시하였는데 그 일부를 제시한 것이다. 그림에서 쉽게 알 수 있듯이 경사제 피복재의 누적피해 거동은 포화모형을 따른다.
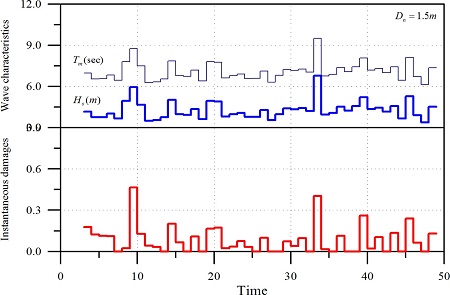
또한 Fig. 10은 Fig. 9의 결과 중 하나의 경로를 나타낸 것으로 시간에 따라 어떤 파랑이 발생되며 그때 어떤 크기의 순간 기대 피해수준이 발생하는지를 살펴보기 위하여 제시하였다. 이는 어떤 순간 기대 피해수준들이 모여 누적 기대 피해수준이 발생되는지를 추적하기 위함이다. 따라서 각각의 연속적인 파고에 따라 발생하는 순간 기대 피해수준을 정량적으로 확인할 수 있다.
따라서 표본경로기법에 의하여 얻어진 Fig. 9의 누적 피해도들을 통계적으로 해석하면 시간에 따른 누적 피해도의 평균을 얻을 수 있다. 이를 식 (1)과 비교하면 μA = 2.5, p = 0.3 그리고 VA = 0.3이 산정된다. 변동계수를 산정하기 위하여 본 연구에서는 Melby(1999)가 제안한 다음 식 (21)을 이용하였다.
따라서 임의의 시간, t1에서 누적 피해도의 평균을 알면 V X t 1 = V A μ X t 1 = 10 = 4.785 V X t 1 = 10 = 0.25
먼저 식 (3)의 WP를 이용하여 추적한 시간에 따른 누적 피해도의 결과를 Fig. 11에 제시하였다. 그림에서 볼 수 있듯이 표본경로기법으로 추적한 Fig. 9의 결과와 매우 잘 일치한다. 비록 본 연구에서 제시한 표본경로기법으로도 시간에 따른 누적 피해도를 추적할 수 있으나 추계학적 확률모형과는 다르게 시간에 따른 누적피해도의 분포함수와 내구년수의 분포함수를 해석할 수 없다. 많은 연구자들이 시간에 따른 제반 거동특성을 확률적으로 해석하기 위하여 추계학적 확률모형을 사용하는 이유이다. 한계수준을 변화시키면서 WP의 식 (6)을 이용하여 산정한 파괴확률을 Fig. 12에 제시하였다. 파괴확률이란 신뢰성 개념과 동일하게 한계수준 α를 초과할 확률을 의미한다. 그림에서 알 수 있듯이 가 작아질수록 빠른 시간에 파괴가 발생된다. 특히 α = 6.0의 경우는 경사제 피복재에서 사용 한계에 해당되는 결과이다. 따라서 Fig. 12와 같은 결과는 구조물의 최적관리에 필요한 기초자료로 유용하게 이용될 수 있다.
비록 WP로도 시간에 따른 누적 피해도의 경로를 추적할 수 있으나 하나 하나의 경로를 따라가다 보면 실제 물리적 현상과 다른 결과를 나타내고 있다. 누적 피해도가 증가하다가 갑자기 감소하는 구간이 존재한다.
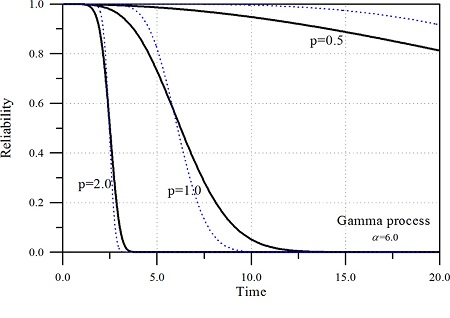
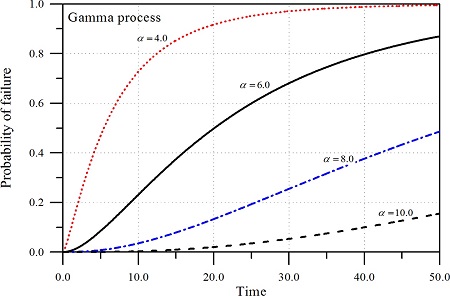
한편 식 (9)로 부터 산정된 매개변수를 이용하여 GP에 의하여 추적된 시간에 따른 누적 피해도를 Fig. 13에 제시하였다. 전반적인 경향이 표본경론기법에 의하여 추적된 Fig. 9나 WP에 의한 결과 Fig. 11과 동일하나 WP에 의하여 추정된 결과 보다 GP의 결과가 약간 작은 쪽으로 추정하는 경향을 가진다. 그러나 GP는 앞에서 설명한 WP가 가지는 한계성을 극복할 수 있다. 또한 GP의 식 (10)을 이용하여 한계수준을 변화시키면서 산정한 파괴확률을 Fig. 14에 제시하였다. WP의 결과인 Fig. 12와 유사한 거동특성을 보이나 가 6.0보다 작은 조건에서는 대부분의 시간에서 파괴확률이 WP의 결과보다 작게 산정한다. 그러나 α가 6.0 보다 큰 조건에서는 반대의 경향을 보이고 있다.
이상과 같이 추계학적 확률과정을 이용하여 경사제 피복재의 시간에 따른 누적 피해도를 추적할 수 있는 방법을 제시하였다. 추계학적 확률과정을 이용하면 자료의 제한에 따른 불확실성과 시간의 진행에 따른 불확실성을 올바로 고려할 수 있다. 또한 누적 피해도의 분포함수와 한계수준에 따른 파괴확률도 시간의 함수로 산정할 수 있다. 따라서 추계학적 확률과정이 갖는 여러 가지 특성들에 주의하여 적용하면 항만구조물의 최적설계나 예방적 유지관리에 필요한 기초자료를 얻을 수 있다.
5. 결 론
추계학적 확률과정을 이용하여 경사제 피복재의 시간에 따른 누적 피해도를 추적할 수 있는 방법을 제시하였다. WP와 GP 그리고 CPP 까지 현재 가장 많이 이용되고 있는 추계학적 확률과정을 제시하였다. 각각의 추계학적 확률과정을 이용하여 누적 피해도가 시간에 따라 어떻게 거동하는지를 추적하였으며, 내구년수의 분포함수와 한계수준에 따른 파괴확률을 시간의 함수로 산정하였다. 특히 본 연구에서는 자료의 제한에 따른 불확실성 뿐만 아니라 시간의 진행에 따른 불확실성도 올바로 고려할 수 있는 방법을 제시하였다. 또한 각 추계학적 확률과정을 적용할 때 주의해야 하는 주요한 특성들도 자세히 해석하였다.
이를 바탕으로 추계학적 확률과정을 경사제 피복재에 적용하였다. 경사제 피복재에 적용하기 위하여 각 확률과정의 매개변수들을 추정할 수 있는 표본경로기법이 본 연구에서 제시되었다. 경사제 피복재의 시간에 따른 누적피해가 포화거동을 따른다는 사실이 확인되었으며 멱함수의 지수가 정량적으로 산정되었다. 이는 추계학적 확률과정을 경사제 피복재에 적용하기 위해서 반드시 필요한 자료로 중요한 의미를 갖는다. 따라서 경사제 피복재의 누적 피해도가 시간에 따라 어떻게 거동하는지를 정량적으로 추적할 수 있었으며, 내구년수의 분포함수와 한계수준에 따른 파괴확률도 시간의 함수로 해석할 수 있었다.
비록 본 연구에서는 경사제 피복재만을 해석하였지만 동일한 개념을 혼성제 케이슨의 활동량 등에도 적용할 수 있다. 따라서 본 연구에서 제시한 추계학적 확률과정과 적용방법을 이용하면 다양한 항만 구조물들을 최적 설계할 수 있으며 예방적 유지관리에 필요한 중요한 자료를 얻을 수 있다.