1. 서론
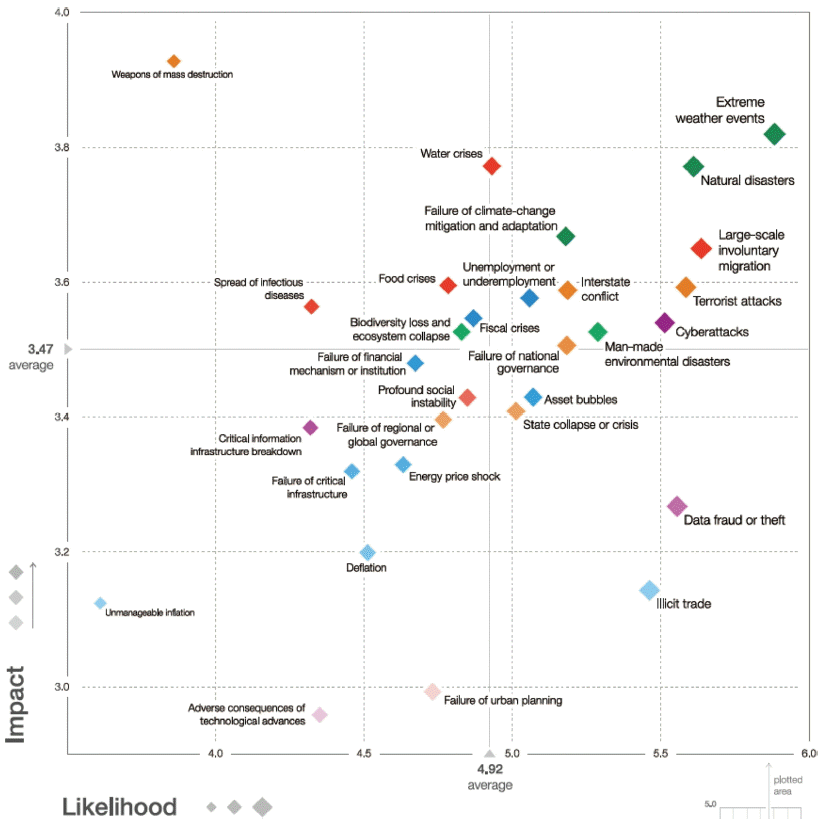
세계경제포럼에서 발표한 세계위험요소 인식조사결과(World Economic Forum, 2017), 극한 기후현상 및 자연재해가 발생 가능성 측면과 그 영향 측면에서 모두 높은 것으로 평가되었다(Fig. 1). 지난해 우리나라 지진관측 역사상 최대 규모의 경주지진 발생, 태풍 차바 내습도 이러한 평가결과와 무관하지 않다. 다행스러운 것은 경주지진 이후 재난안전에 대한 국민적 관심이 높아져, 유비무환의 지혜를 깨닫는 기회가 되었다는 점이다.
삼면이 바다로 둘러싸인 우리나라는 파랑으로부터 국가 기반시설인 항만 내 시설물을 보호하는 역할을 담당하고 있는 방파제에 대해 극한 기후변화에 대한 선제적 대응이 필요하게 되었고, 그 일환으로 부산 감천항 방파제가 2013년에 보강되었으며, 포항 영일만 북방파제와 부산항 조도·오륙도 방파제 보강이 확정되어 추진되고 있다. 그러나, 이러한 보강은 2005년 심해 설계파에 기초하여 이루어지고 있어, 향후 심해설계파가 개정이 되면(2018년 예상), 추진되고 있는 보강계획 및 기 보강된 방파제의 안정성에 대한 전면적인 재검토도 필요하게 될 것으로 판단된다.
최근 발생한 대형 태풍으로 인한 방파제 피해 사례를 보면, 2011년 8월 제9호 태풍 무이파(MUIFA)에 의해 가거도방파제가 큰 피해를 입었고, 2012년 8월 제15호 태풍 볼라벤(BOLAVEN)의 내습으로 서귀포항 외곽방파제에 상치 콘크리트가 파손되고 TTP가 대규모로 유실되는 등 막대한 피해가 발생하였다. 서귀포항의 경우에 2003년 9월 제14호 태풍 매미(MAEMI) 내습 시에도 유사피해가 발생한 이력이 있다(Lee, 2014). 이어, Fig. 2에서 보이는 바와 같이 2016년 제 18호 태풍 차바(CHABA)의 영향으로 부산 감천항 및 다대포항 방파제가 크게 파손되면서 원인 규명 및 막대한 복구 마련에 어려움을 겪고 있다. 이처럼 방파제는 한번 피해가 발생하면 보수가 용이하지 않기에 사전에 피해를 막는 방안모색이 시급한 실정이다(Seo et al., 2015).
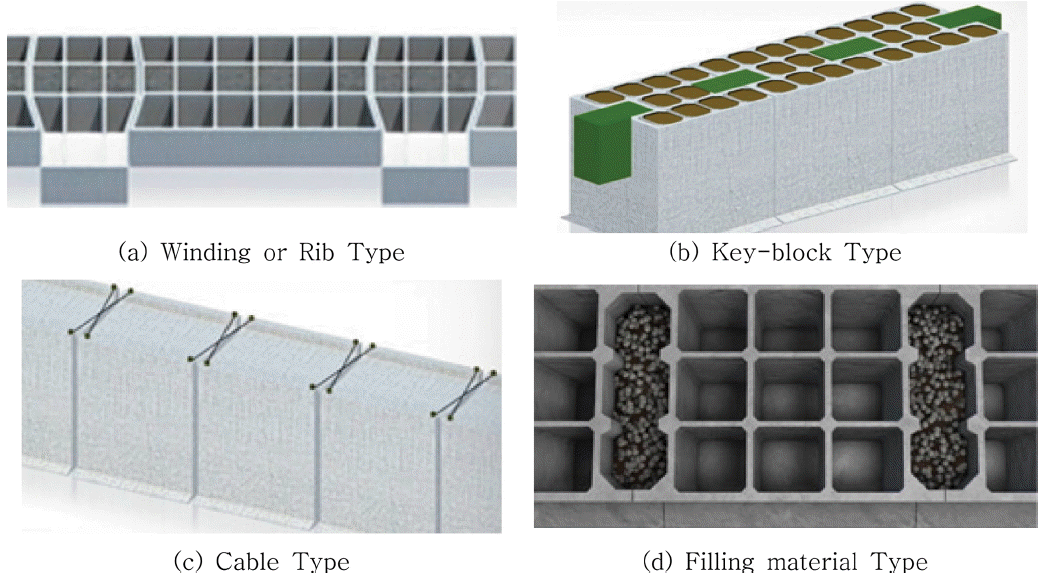
최근, 방파제의 안정성을 높이기 위하여, 독립적으로 설치하는 방파제 케이슨을 인접 케이슨과 서로 인터로킹시켜 외력에 대해 연대해서 저항하는 방안이 시도되고 있다(Hyundai Dvp Company, 2009, 2011; Park et al., 2011). 현재까지 제안되어 연구되고 있는 인터로킹 방법으로는 요철형, 키블록형, 케이블형, 채움재형 등이 있다(Fig. 3).
인접 케이슨을 서로 인터로킹시키면 작용 최대파력을 저감할 수 있어 인터로킹되지 않은 경우에 비하여 안정성이 크게 향상된다. Seo et al.(2015)은 단순화된 정적 선형모델을 이용하여 인터로킹 케이슨 방파제에 대한 파력분산특성에 대해서 연구한 바 있으며, 위상차 효과로 방파제에 작용하는 최대 파력이 하나의 케이슨에 작용하는 최대파력 보다 감소함을 살펴본 바 있다. 또한 설계파고 보다 큰 이상파랑 작용시 비선형 거동에 대해서 Park et al.(2015)이 해석한 바 있다. 해양수산부에서는 이러한 추세를 반영하기 위하여 연구용역을 수행하고(MOF, 2015), 이를 근거로 2016년 4월 항만 및 어항 설계기준·해설[부록] 개정안에 “7편 장대형 케이슨에 발생하는 파력 평활화 효과”를 추가한 바 있다. 케이슨 인터로킹에 의한 방파제 장대화에 따른 파력 평활화 효과가 제시되기는 했지만, 현재, 설계기준에 제시된 안정성 평가식으로는 장대 방파제의 안정성을 충분히 평가하기는 어렵다. 특히, 설계파 작용 시 해상상태를 실제와 가장 유사한 다방향 불규칙파로 정의하는 경우에는 현재 제시된 식으로는 파력 평활화 효과를 고려할 수 없다. 따라서, 본 연구에서는 다방향 불규칙파 조건에서의 파력 평활화 효과를 고려하여 케이슨 인터로킹에 의해 장대화된 방파제의 안정성을 기존 안정성평가 개념 범위 안에서 용이하게 평가할 수 있는 방법에 대해서 연구하였다.
방파제에 경사 입사하는 파의 위상차는 선형 중복파 이론에 기초하여 고려하였으며, 설계파의 비선형성을 적절히 고려하기 위하여 파압의 연직방향 및 바닥면에 대한 단위 폭당 파압 분포를 설계기준에서 적용하고 있는 Goda 파압식(Goda, 2010)에 따르는 것으로 하였다. 이러한 가정을 바탕으로 방파제 전체가 일체 거동하는 것으로 보고, 방파제 법선 방향 미끌림에 대한 안정성 평가식을 유도하였다.
2. 안정성 평가식 유도
2.1 작용파력
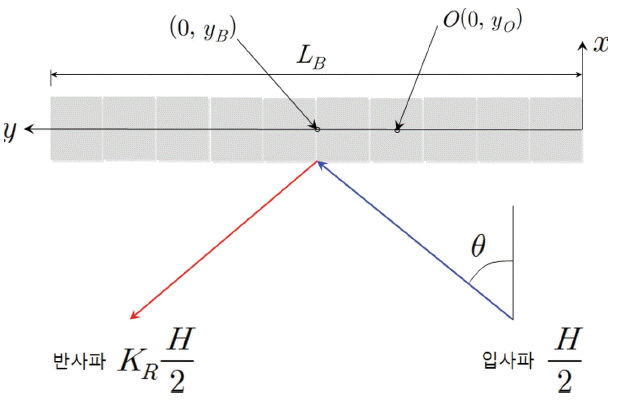
Fig. 4와 같이 파고가 H, 진동수가 ω인 규칙파가 수심이 h인 해역에 설치된 LB 길이를 가지는 방파제에 경사각 θ로 입사하는 입사파에 의한 파압 및 파력을 산정하기 위하여, 무한 방파제에 경사로 입사하는 선형파에 대한 해석해를 이용하였다. 방파제 기준선에 직각 방향을 x, 기준선 방향을 y, 정수면으로부터 연직방향을 z로 가지는 직교좌표계(x, y, z)를 사용하였다. 즉, 반사율 KR인 방파제에 작용하는 동압력, P에 대한 해석해(Jung et al., 2015)는 식(1)과 같이 표시된다.
여기서,
ρ는 해수밀도, g는 중력가속도를 의미하며, k는 분산관계식을 만족하는 입사파의 파수이다.
케이슨에 작용하는 수평파력 FX는 동압력 P를 작용면적 A에 대하여 적분하여 구할 수 있다. 즉,
(2)
여기서,
γd는 파력 평활화계수로 알려져 있으며(Takahashi and Shimosako, 1990; Burcharth and Liu, 1998), 케이슨에 작용하는 최대파력을 파압의 위상을 고려하지 않고 산정한 최대파력(방파제에 직각으로 입사하는 파에 의한 최대파력)으로 나눈 것으로 정의된다.
케이슨 바닥에 작용하는 바닥에 작용하는 양압력에 의한 연직파력 FZ는 바닥면에서의 동압력, P를 작용면적, A에 대하여 적분하여 구할 수 있다. 방파제 폭(WB) 방향으로 동압력 분포를 선형적으로 감소하는 삼각형 분포로 가정하면 다음과 같이 연직파력을 구할 수 있다.
(4)
식(2)와 (4)는 선형파 이론에 기초한 파력으로, 파고가 높아 비선형성이 큰 설계파와는 차이를 보일 수 있다. 따라서, 설계에 적용하기 위해서 현행 설계기준에서 제시하고 있는 Goda 파압식을 이용하여 설계파력을 재 정의하였다. 즉, 식(2)와 (4)에서 작용파력 부분(γd 이전까지의 항)을 Goda 파압을 적용한 파력으로 대체하여 다음과 같이 정의하였다.
여기서, F X D F Z D F X G F Z G
설계파를 일방향 불규칙파로 할 때의 설계파력분포는 불규칙파에 대한 평활화계수, y i X y i Z
여기서, F X G F Z G y i X y i Z
여기서, Sη(ω)는 설계입사파 스펙트럼을 나타낸다.
설계파를 다방향 불규칙파로 할 때의 설계파력분포는 일방향 불규칙파의 경우와 같이 다방향 불규칙파에 대한 평활화계수, y m X y m Z
여기서, F X G F Z G y m X y m Z
여기서, Sη(ω, θ)는 다방향파에 대한 스펙트럼을 나타낸다.
2.2 미끌림 안정성 평가식
설계기준에서는 미끌림에 대한 안전율(SF)을 연직 최대 작용력에 의한 마찰력과 작용 최대 수평파력의 비로 정의하고 있다.
여기서, μ는 정지마찰계수, We는 부력을 제외한 방파제의 유효자중을 의미한다. 이러한 정의는 수평 및 연직 최대파력이 동위상으로 작용하는 경우에는 유효하지만, 위상차를 보이는 경우에는 합리적이지 못한 결과를 주게 된다. 따라서, 본 연구에서는 안전율을 시간에 대한 불변항인 유효자중에 의한 마찰 저항력과 시간 변동항인 케이슨 바닥면에 작용하는 연직파력의 영향이 고려된 최대 수평방향 작용파력의 비로 식(11)과 같이 새롭게 정의하였다. 즉, 미끌림 방향 최대 작용파력을 케이슨에 작용하는 수평방향 파력에 케이슨 바닥면에 작용하는 연직방향 파력의 부마찰력의 합으로 정의하였다.
여기서, γj는 작용파력 평활화계수로 설계파 종류에 따라 다음과 같이 표현된다.
▪ 규칙파의 경우(j = r),
▪ 일방향 불규칙파의 경우(j = i),
▪ 다방향 불규칙파의 경우(j = m),
3. 결론
본 연구에서는 인터로킹된 케이슨에 의한 장대형 방파제의 미끌림에 대한 안정성 평가식에 대해서 연구하였다. 선형파 이론에 기초하여 경사 입사하는 파랑의 작용 위치별 위상차의 효과를 고려하였으며, 최대 연직파력분포는 설계기준의 Goda 파압식을 적용하였다.
안전율(SF)를 방파제 유효자중에 의한 마찰저항력과 파에 의한 수평 및 수직 파력에 의한 작용파력의 비로 정의하고, Goda 파압식에 의한 수평 및 연직파력과 파압 위상차에 기인한 작용파력 평활화계수로 표현하였다. 작용파력 평활화계수를 규칙파, 불규칙파 및 다방향 불규칙 조건에 대하여 각각 제시함으로써 모든 설계파에 대해서 적용 가능하도록 하였다.